关于二次曲线一般理论教学的思考

(岭南师范学院数学与统计学院，广东 湛江524048)

0 前言

当前，很多地方师范院校正在向应用型高校转型，在转型的过程中，涉及多方面的改革，课程改革则是其中重要的环节。解析几何是高师数学专业的重要基础课，随着教学改革的深入，解析几何课程也面临着一些问题，其中最为突出的问题是课时量少，教学任务繁重。以笔者所在学校为例，目前解析几何课程的课时量缩减为48课时，要用48课时完成解析几何的教学任务，教学工作是比较繁重的。因此，在解析几何的教学中，如何合理处理教材，精简教学内容变得非常重要。

吕林根、许子道主编的《解析几何》(第四版)[1]是师范院校数学专业普遍采用的教材, 按教学计划，教师一般会讲授一至五章内容，其中第五章主要研究二次曲线的一般理论，这部分内容在解析几何课程中占有很重要的地位，但是由于课时的关系，每次讲到这里的时候，所剩的课时不多，因此如何用比较少的课时把这一部分内容讲清楚，是对教师的一个考验。文章主要以吕林根、许子道主编的《解析几何》(第四版)[1]为例，结合本人在教学过程中的一点经验，谈谈如何合理地处理该教材中的第五章内容，也即是二次曲线的一般理论。

1 删除二次曲线切线及主直径内容

解析几何二次曲线一般理论的主要内容为二次曲线的化简与分类。在化简二次曲线方程时，教材共介绍了三种方法，分别为：1.利用移轴和转轴化简二次曲线方法；2.利用主直径化简二次曲线方法；3.利用不变量化简二次曲线方法。由于课时的关系，在教学过程中，这三种方法不可能全部介绍，需根据实际情况进行选讲。对于方法1，由于该方法是化简二次曲线的基本方法，并且，该方法思想简单，学生容易接受，因此，方法1在教学过程中必须介绍。对于方法3，在已经清楚二次曲线的分类之后，学生学习这一部分内容也相对容易，教师组织教学也不会太难，花费教学时间也不会太多，因此方法3也可以介绍。至于方法2，由于该方法的预备知识为直径和主直径，为了介绍该方法，还得花大量的时间去介绍直径和主直径的相关理论，因此，出于课时的考虑，可以不介绍方法2。在不介绍方法2的情况下，教材中介绍直径和主直径相关理论的第五章4、5节也就可以省略掉。至于二次曲线的切线，即本章的2节内容，由于知识相对独立，去掉这部分内容，不会影响本章的完整性。因此，在课时紧张的情况下，可以把第五章的2、4、5节的内容省略掉，既不影响内容的完整性，也不影响核心内容的教学，还可以大大节省教学时间，真正达到精讲的效果。

2 重新证明简化公式

关于二次曲线的分类，其理论依据主要是教材[1]中的定理5.6.1,也即以下的定理3.1教材中的不变量方法，也是基于该定理进行化简与分类。但是在教材[1]中，该定理的证明要利用到主直径的相关理论，而上文已经提到，如果课时紧张，可把直径和主直径相关理论砍掉，为了保证知识的连贯性，这样就要求对教材[1]中的定理5.6.1给出一个不需主直径相关理论的证明方法。本节主要介绍如何利用移轴、转轴和配方的方法证明以下定理3.1。

定理3.1[1]适当选取坐标系，二次曲线的方程总可以化成下列三个简化方程中的一个：

(1)ɑ11x2+ɑ22y2+ɑ33=0，ɑ11ɑ22≠0；

(2)ɑ22y2+2ɑ13x=0，ɑ22ɑ13≠0；

(3)ɑ22y2+ɑ33=0，ɑ22≠0．

证明：设二次曲线方程C为

ɑ11x2+2ɑ12xy+ɑ22y2+2ɑ13x+2ɑ23y+ɑ33=0

则在转轴公式

(3.1)

下，二次曲线C的新方程为

其中，

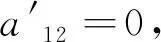
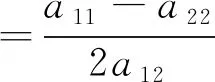
(3.2)

因为余切值可以取到任意实数，所以总有满足上面的条件, 也就是说，总可以通过适当转轴消去方程中的交叉项xy，即二次曲线方程C总可以通过转轴化为以下方程

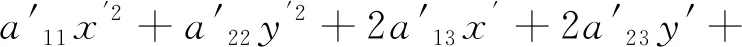
(3.3)

对于方程 (3.3)，通过移轴，可以对其进一步化简．如果C为中心二次曲线，设 (x0,y0)为二次曲线的中心，作移轴变换

(3.4)

则在新坐标系下，原方程可化为以下的简化形式

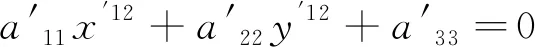
(3.5)

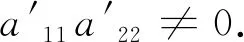
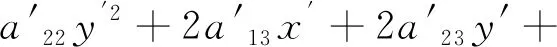
上式左端关于y′配方可得

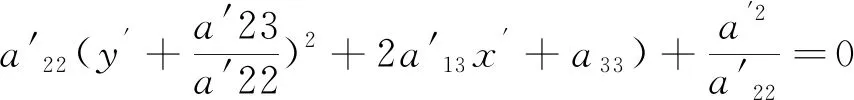
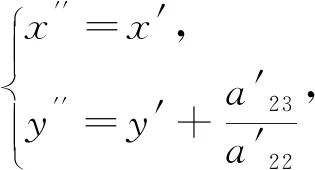
(3.6)

则(3.6)可进一步化简得到

(3.7)

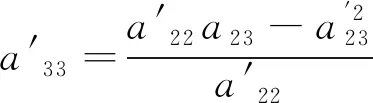
(3.8)

去掉(3.5)，(3.7)，(3.8)的撇号，可得到定理3.1的结论。

从以上的证明可以看出，不借助主直径相关理论方法，也是可以得到二次曲线方程的分类定理。从这角度来看，在教学中去掉直径和主直径的教学内容，是不会影响到本章系统的完整性的。因此本文所介绍的教材处理方法是可行的。

定理3.1的证明过程也即是利用移轴和转轴化简二次曲线的过程，该过程的要点为： 1) 首先利用转轴消去交叉项xy；2)然后通过配方得到移轴公式，从而化方程为最简。利用以上化简过程，任何的二次曲线方程都可以化为最简。下面通过例子介绍该过程。

例3.1：化简二次曲线方程

x2+2xy+y2+2x+y=0

解：此方程含有交叉项，按照定理3。1证明的方法，可以先转轴消去交叉项xy。为此，可设旋转角为ɑ，由(3.2)，可得

cot2ɑ=0 ，

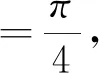
把上式代入原方程化简整理得转轴后的新方程为

对上式配方整理得

(3.9)

根据(3.4)，可得移轴公式

事实上，如果二次曲线是中心二次曲线，借助二次曲线的中心，也可以先移轴，再转轴。

例子3.2 化简二次曲线方程

x2-xy+y2+2x-4y=0

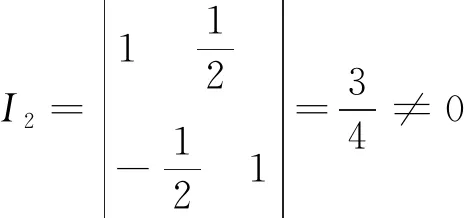
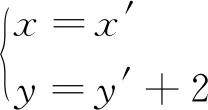
x′2-x′y′+y′2-4=0

(3.10)

为了消去(3.10)的交叉项，根据(3.2)，我可得

cot2 ɑ=0 ，

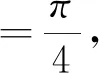
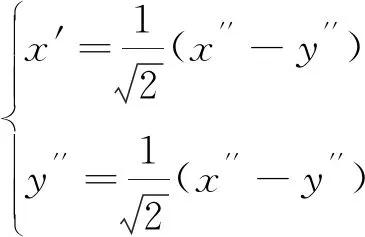
代入(3.10)，可得简化公式为

x′′2+3y′′2-8=0

注： 例子3.2的解法是先移轴，再转轴，其基本思想是：首先平移坐标系使得坐标原点与二次曲线的中心重合，从而消去一次项及，然后，再通过转轴，消去交叉项，从而化二次曲线为最简。但该方法有局限性，如果二次曲线为非中心二次曲线，若先移轴，就比较困难建立移轴公式，此种情况就得先转轴，再移轴。

3 小结

二次曲线的一般理论是解析几何课程中的一个重要的内容，但是由于课时的关系，教师在讲授本部分内容时不可能面面俱到，因此在不改变内容完整性的基础上对本部分内容进行重新调整很有必要。对于教材[1]第五章(二次曲线的一般理论)的教学，如果不介绍利用主直径方法化简二次曲线，同时对教材定理5.6.1的证明作适当的处理，则去掉5.2节(二次曲线的切线)、5.4节(二次曲线的直径)和5.5节(二次曲线的主直径与主方向)的内容是完全可以的，这样的处理也不会影响知识的完整性。事实上，通过对教材[1]作这样的处理后，学生对这章的学习变得轻松，教师的教学也变得从容，从而克服课时减少带来的种种弊端。