航空发动机涡轮轮缘封严数值模拟

陶立权，马 振，邱学旺

（1.中国民航大学适航学院，天津 300300；2.华夏航空有限公司重庆分公司，重庆 401100）

涡轮是航空发动机核心机部件之一，在高温高压的恶劣环境下工作，不但强度要承受考验，更受到高温燃气的不断侵蚀，是整个发动机中最易损坏的部件。因此为保障发动机安全可靠运行，改善涡轮的工作环境，使之安全高效地工作，值得深入研究和探索。

涡轮盘作为重要的承力部件，静子轮盘与转子叶盘之间存在腔室，转静叶盘构成的腔室面临的主要问题是避免高温高压燃气通过轮缘之间的间隙入侵到腔室内部。受轮盘材料耐热性限制，一旦燃气入侵，势必导致轮盘过热，从而降低整个发动机的效率，甚至造成严重故障。

目前常采用冷空气对涡轮盘进行冷却，这部分气体被称为封严冷气，过少的封严冷气达不到预期的效果，而过多的封严冷气会降低发动机性能。研究[1]表明，入侵燃气浓度在盘腔内增加1%，转盘的寿命会降低50%；减少50%封严冷气量，燃气涡轮的整体效率会提高0.5%，同时燃油消耗率会减小0.5%。因此，当通入的封严冷气流量正好使得盘腔系统没有燃气入侵时，这时的冷气量被称为最小封严流量。

Jakoby 等[2]根据试验得到的涡轮盘腔压力频谱分析出当封严冷气体积低于一定值，涡轮盘腔中的大涡结构会在80%动盘转速下旋转，导致更严重的燃气入侵。Steve 等[3]通过试验发现，增加封严冷气的流量直到足够大时，涡轮盘腔中旋转的大涡结构消失，此时静子导流叶片和旋转叶片的相互作用变成了燃气入侵的主要因素。O′Mahoney 等[4]通过模拟大涡结构获得燃气入侵的物理现象，与其试验结果很接近。Green 等[5]根据试验现象发现，完全阻止燃气入侵，需增大轮盘盘腔内封严处的压力，直至与主流总压或动叶前缘的相对滞止压力相等。孙纪宁等[6]通过体积分数法测量了几种转静系中的最小封严流量，研究了封严结构的最佳形式。周昆原等[7]利用计算流体动力学方法对轴向封严结构进行研究，探索了不同封严流量下，盘腔压力、封严间隙处径向速度的变化规律，并得到相应的最小封严流量。高庆等[8]通过对比数值模拟与实验结果，得出不同动静叶盘轴向间距对封严效率的影响，以及轮缘密封轴向的位置对封严效率的影响。

分析以上研究可知，相关学者在研究涡轮轮缘封严时主要采用压力参数法、浓度效率法和质量效率法。

对比这3 种方法，在确定最小封严流量时，压力参数法通过比较涡轮盘腔内参考点的静压（P2）和外部参考点静压（P1）得到最小封严流量，P2 ＜P1，表示系统未封严，P2=P1 表示系统恰好封严，此时的封严流量就是最小封严流量，然而实际测量计算中，压力参数法得到的最小封严流量与参考点位置的选取有关，往往会高估最小封严流量，对于保护轮盘腔而言，虽然有利但采用此最小封严流量偏于保守；浓度效率法用于实验研究中，需要测量参考点、主流入口和封严冷气入口的示踪气体浓度，然后转化为标量方程，由此计算出浓度效率，具有较好的工程应用价值，但对实验室条件具有较高要求；质量效率法，首先假设流动为定常不可压流，采用对应质量效率为99%时的封严冷气流量来作为最小封严流量，然而在封严流量不为0 时，质量流量效率均在90%以上，封严流量调节范围较小，这不便于更好地通过改变封严流量来确定最小封严流量。

因此，为增强研究成果的说服力和提高科研精度，在数值模拟研究中，采用压力参数法和质量效率法相结合的方法。首先采用压力参数法确定最小封严流量，然后用质量效率法进行结果校正，以保证结论的可靠性和准确性。

文中几何模型中相关数据参考英国Bath 大学涡轮轮缘密封实验参数，通过CFD 软件ANSYS CFX 15.0数值求解二维RANS 方程组和SST 湍流模型，采用压力参数法确定最小封严流量，研究涡轮轮缘双层轴向封严中，内层封严在不同高度下对封严效率的影响。

1 计算模型与数值方法

1.1 数值计算模型

轮缘密封结构模型[9]如图1所示，轮缘密封和涡轮盘腔结构的主要几何参数如表1所示。轮缘密封间隙比Gc，ax=Sc，ax/b=0.010 5，Sc，ax为密封间隙，b为轮缘端壁面半径；盘腔间隙比G=S/b=0.105，S为动静盘腔间隙。封严结构为轴向封严，盘腔冷却结构为中心进气冷却结构。轴向封严结构的计算域网格如图2所示，应用ICEM CFD 15.0 进行网格划分，在Blocking 中建立相互对应的关系，并设置网格密度。边界处对网格加密处理，在内部其余部位网格加粗，以保证求解精度、缩短计算时间。

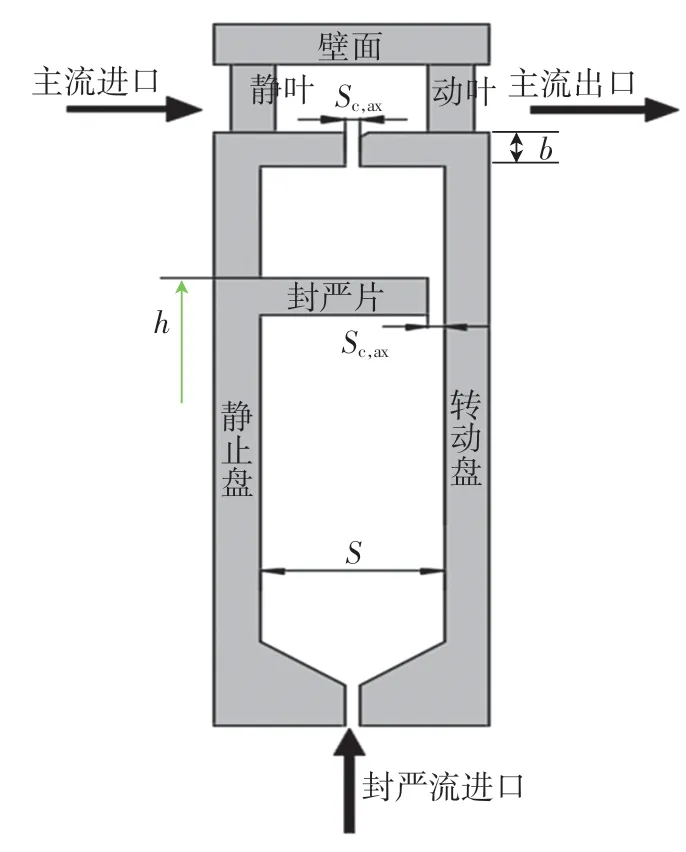
图1 轮缘密封结构模型Fig.1 Rim sealing structure model

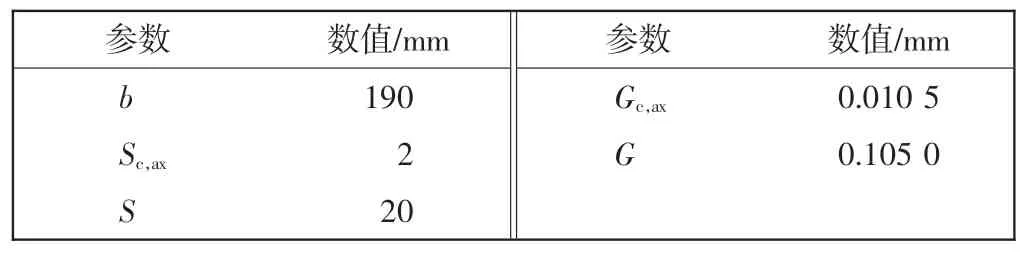
表1 轮缘密封结构的主要几何参数Tab.1 Main geometric parameter of rim sealing structure

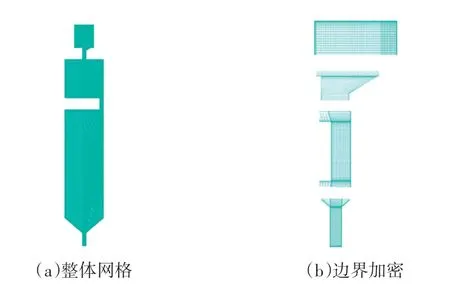
图2 轴向封严结构计算域网格Fig.2 Computational domain grid of axiel sealing structure

1.2 流体力学基本方程组与湍流模型

流体力学基本方程组的控制方程包括：连续性方程、动量方程、能量方程。

连续性方程为

动量方程为

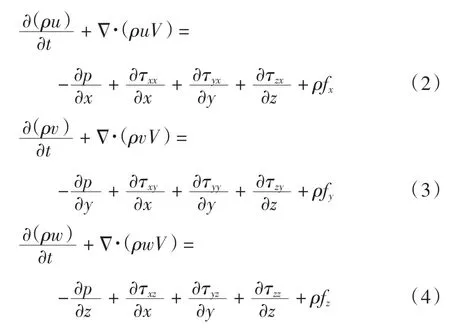
能量方程为

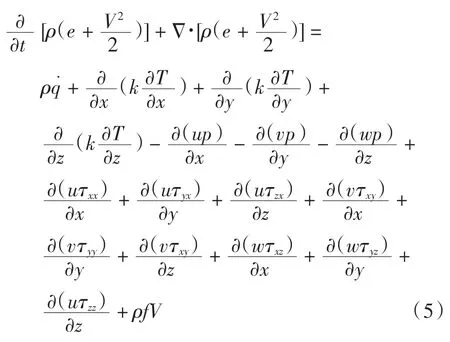
控制方程中各项的物理意义参照文献[10]。当前应用最普遍的湍流模型是k～ε模型，而该模型存在以下不足之处：①湍流尺度未知；②仅适用于湍流边界层压力相对稳定的情况；③其壁函数在边界层的修正中难以弥补计算模型与实际物理现象之间的差距。相对于该模型，SST 湍流模型具有以下优势：①适应压力梯度变化的各种物理现象；②可应用粘性内层，通过壁函数的应用，精确模拟边界层现象，无需使用较易失真的粘性衰减函数。因此采用SST 湍流模型进行计算。

1.3 数值方法

采用ANSYS CFX 15.0 求解RANS 方程组，选取SST 湍流模型，模型定义如表2所示。该模型模拟稳定状况下的流动，工质采用理想空气；时态选择稳态；流体可压缩，类型选择基于压力；速度为绝对速度；讨论二维平面无对称轴问题，选择二维空间。同时该流动问题为可压缩流动，有能量传递问题，故选择能量方程。边界条件具体设定值如表3所示。依据文献[9]设定的边界条件，同时按照计算方法可行、数学适用及工程合理的原则进行设定。主流进口流量为2 kg/s，水力直径为0.01 m，温度为1 600 K；封严进口流量初始值设置为0，温度为323 K；主流出口类型为压力出口，温度为1 600 K；其余静止盘和转动盘保存为默认选择。计算过程中，设置连续方程、动量方程及能量方程的收敛值为1e-6，当各计算结果小于该设定值时，表示结果已经收敛，计算停止。

表2 模型定义Tab.2 Model definition

表3 边界条件Tab.3 Boundary condition

数值计算采用压力参数法确定最小封严流量Cω，min。参考图3，如上文所述，当压力P2 ＜P1 时，表示未完全封严；当P2=P1 时，表示恰好完全封严，此时的封严流量就是最小封严流量Cω，min，即Cω，min=Cω。

压力测点的选定：涡轮盘腔内测量静压P2的参考点位置为静止盘上r/b=0.95 处（r为测量点位置），与文献[11]一致，测量外部静压P1的参考点为距封严前缘5 mm的位置，对应文献[12]的测压位置。据此两压力测点位置即（7，1952）、（0.2，1805）。

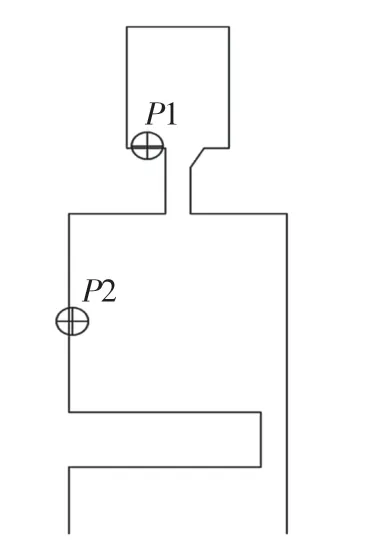
图3 压力参数法Fig.3 Pressure parameter method

增加封严流量，其他保持不变，初始化后再进行运算，比较P1与P2 大小，再调整封严流量大小，直到两压力测点的压力差约等于0，此时的封严流量即为最小封严流量Cω，min。利用该方法可以找到不同内层封严高度h 下的模型最小封严流量Cω，min。

1.4 数值方法验证

用质量效率法验证压力参数法的可靠性。根据质量守恒定律，在封严间隙处，流入和流出的流体关系为

由上式可将质量流量效率[4]定义为

流量公式为

其中：m为质量流量；ρ为密度；A为面积；v为速度。由于封严冷气与主流热气来自同一气源系统，不同径向半径处的密度相等，且封严流入口和出流口通道宽度相等，即通道面积相等，所以，要比较其流量，就相当于比较通过截面的流速。

2 结果分析

利用上述压力参数法可找到不同内层封严高度h下的最小封严流量Cω，min，测点的压力值及其差值ΔP =P1-P2 如图4所示。

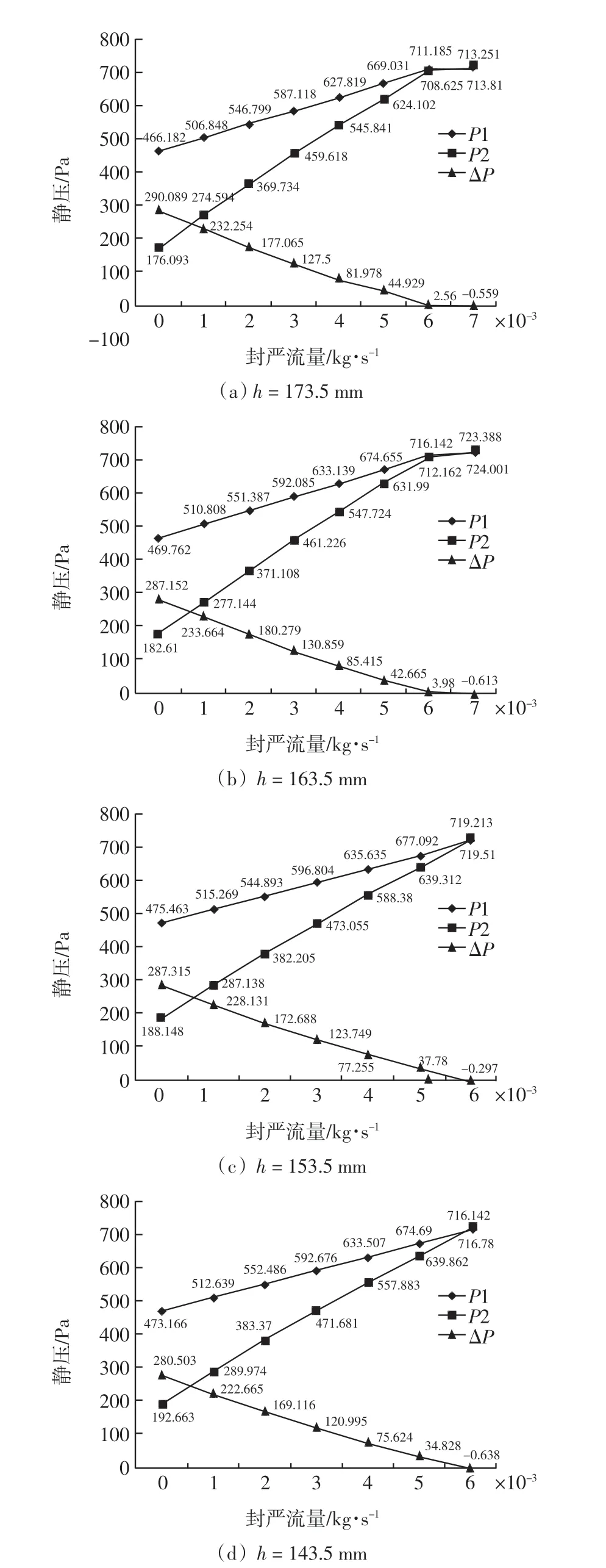
图4 不同内层封严高度h 下的测点静压Fig.4 Pressure at measuring points under different internal sealing heights

分析图4 可知，随着封严流量的增加，封严腔内压力P2 增大，同时由于腔内封严气体外流至主流，导致腔外主流压力P1 增加，但腔外主流压力的增加速度小于腔内压力的增加速度，因此封严腔内外的压力差值ΔP=P1-P2 逐渐减小，直至压力差为0，达到完全封严。

可以看出，内层封严层位置从h=173.5 mm 到h=143.5 mm，最小封严流量只在6e-3 到6.15e-3 之间变化，其变化差值为0.15e-3，相对6.15e-3 变化率仅为2.5%。由此可以得出：双层轴向封严内层封严层高度位置h 对封严效率几乎没有影响。

采用质量效率法得到不同内层封严高度h 下的最小封严流量如图5所示。可以看出，在封严流量不为0 时，其质量流量效率均在90%以上。如前所述，最小封严流量可用质量流量效率为99%时的封严流量来表示。所以，质量流量效率法下的最小封严流量在0.005 5～0.0061 kg/s 之间，而压力参数法下的最小封严流量在0.006～0.006 15 kg/s 之间。比较分析可知，两者吻合良好，验证了所建几何模型与压力参数法的可靠性和准确性。应当说明，采用不同方法测得的最小封严流量有微小差别，压力参数法所得数值大于质量效率法，与文献[7]结论一致。但采用质量效率法时，由于最小封严流量用质量流量效率为99%时的封严流量来表示，不便于更好地改变封严流量来确定最小封严流量，压力参数法能较好地确定最小封严流量。

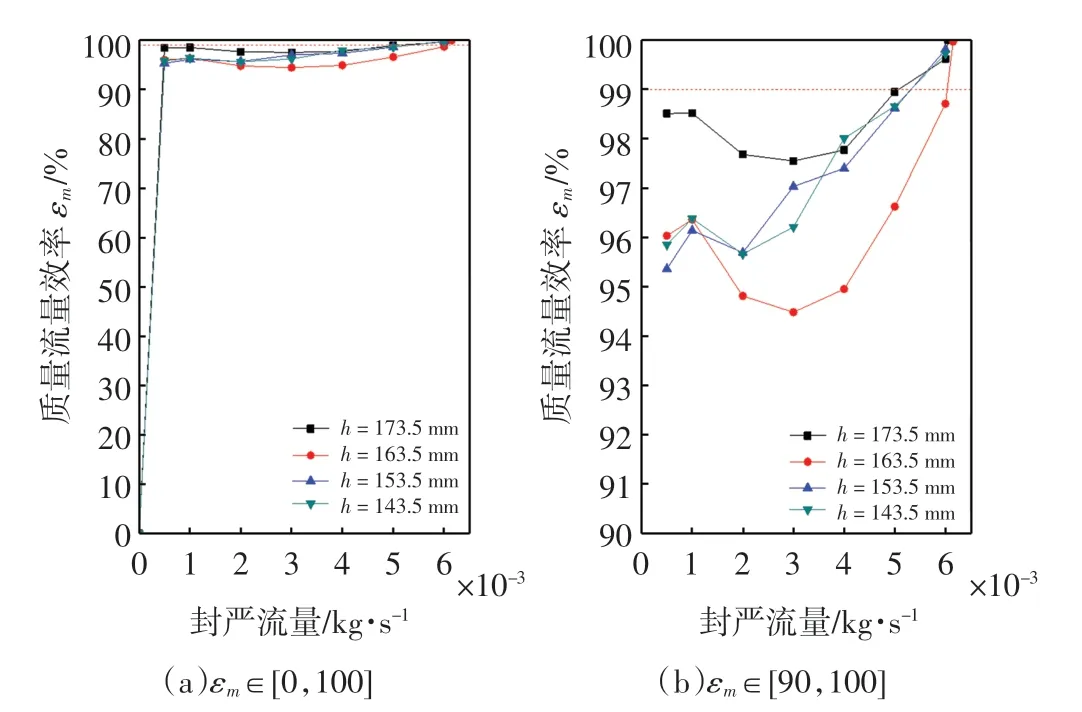
图5 质量流量效率Fig.5 Mass-flow efficiency

封严流量Cω=0 kg/s 时单层轴向封严和双层轴向封严各内层不同封严高度的静温云图如图6所示。

可以看出，在Cω=0 kg/s 时，单层轴向封严的封严腔几乎被高温气体所覆盖，且温度与主流气体十分接近。该情况下，封严腔必然会受到高温气体的直接烧蚀，长时间的作用导致封严腔受到极大损伤，所以必须通入封严冷气以保护封严腔室。

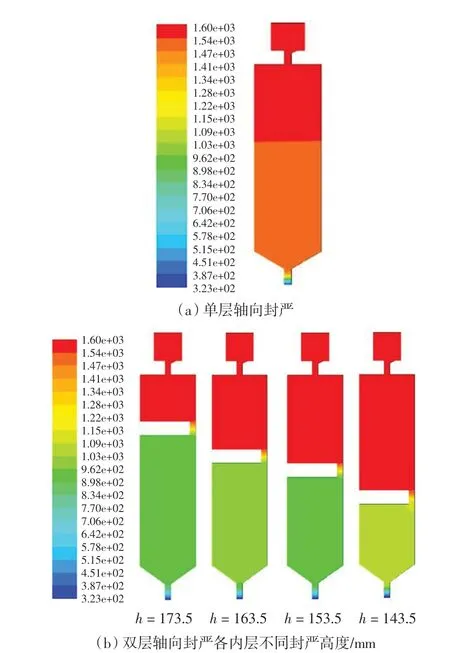
图6 静温云图Cω=0 kg·s-1Fig.6 Static temperature nephogram with Cω=0 kg·s-1

而对于双层轴向封严，当Cω=0 kg/s 时，轮盘腔高半径处已基本被高温气体所覆盖，温度接近主流高温气体；而内层封严刚好作为一个分界线，温度在内层封严缝隙处发生了极大降低。封严腔低半径处温度相对主流高温气体有很大的降低，说明内层封严对于主流高温气体有很好的阻隔作用，相对于单层轴向封严，双层轴向封严对于涡轮封严腔有更好的保护作用。很明显，此种情况下必须增加封严气体以改善封严效果。

封严流量Cω= 0.001 kg/s 时，单层轴向封严和双层轴向封严各内层不同封严高度的静温云图如图7所示。可以看出，单层轴向封严，当封严流量Cω=0.001 kg/s 时，冷气充满整个封严腔，高温主流气体退出。在轴向封严入口处，高温主流气体与封严冷气掺混，温度变化较大。而封严流量0.001 kg/s 相对于主流流量2 kg/s 占比很小，可见用通入封严冷气来进行密封，效果十分明显。而对于双层轴向封严，当封严流量Cω=0.001 kg/s 时，封严腔的高温区域明显减少，基本被封严冷气所填充。不同的内层封严高度下，温度分布区别不大。但该封严流量下，外层封严入口区域与主流接触处，由于封严冷气与主流高温气体掺混，使温度产生较大变化。说明封严冷气对封严腔（涡轮盘腔）的保护作用十分明显，也再次说明封严冷气对于防止燃气入侵的可行性。

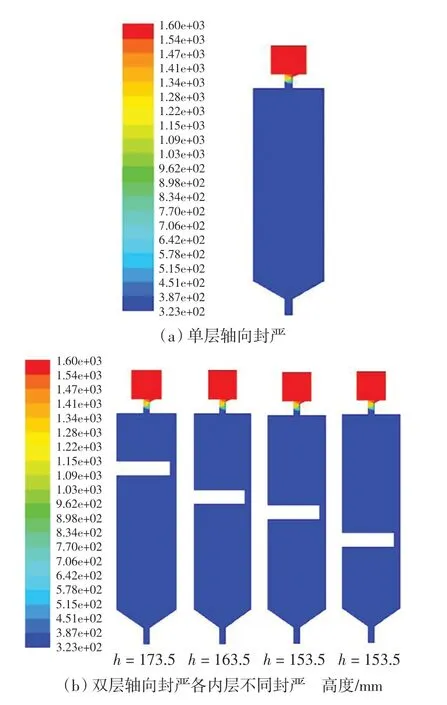
图7 静温云图Cω=0.001 kg·s-1Fig.7 Static temperature nephogram with Cω=0.001 kg·s-1

由于封严冷气充满整个封严腔，使高温主流气体很难进入封严腔，同时由于主流气体与封严气体在外层封严入口区域发生热交换作用，使温度发生较大变化，导致单层轴向封严效果与双层轴向封严效果在图7的静温云图上很难看出明显区别。

3 结语

1）随着封严流量的增加，主流压力测点与封严腔压力测点的压力差值逐渐减小，燃气入侵逐渐减小。当主流压力测点与腔内压力测点的压力值相等时，达到完全封严，此时的封严流量为最小封严流量，即防止燃气入侵所需的最小封严流量。

2）随着封严流量增加，封严腔内压力增大，腔内封严气体外流至主流，导致腔外主流压力增加，因此会对主流压力产生影响，使之增大。

3）从结果来看，由于封严冷气充满整个涡轮盘腔，使高温主流气体很难进入封严腔，同时由于主流气体与封严气体在外层封严入口区域发生热交换作用，使主流气体温度发生较大变化，导致双层轴向封严中，内层封严片的高度位置对封严效率没有什么明显的影响。

4）在封严流量不为0 时，其质量流量效率均在90%以上，且最小封严流量可以用质量流量效率为99%时的封严流量来表示，所以其范围过小，不便于调整入口封严流量来确定最小封严流量。

5）当封严流量为0 时，相对于单层轴向封严，双层轴向封严对涡轮封严腔室有更好的保护作用。