基于外符合精度的RTK高程拟合三角形网格法

焦卫东，曾岚风

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

近年来，基于实时动态（RTK，real time kinematic）载波相位差分技术定位的测量技术应用越来越广泛，可快速准确地获得高精度的三维测量数据，不仅极大提高了工作效率，且减轻了野外劳动强度，是民航飞行程序设计、机场建设等控制测量作业的首选方法[1-2]。但RTK 测量存在基准面的缺陷，导致高程误差较大，因此，提出高程拟合方法。

高程拟合方法是对观测点进行几何水准联测，同一点的大地高减去正常高得到该点的高程异常，再把测区的似大地水准面假定为多项式曲面或其他数学曲面来拟合已知高程异常点，拟合的曲面内插其他点的高程异常值。常规拟合法分为线性拟合模型、平面拟合模型和曲面拟合模型（含多项式拟合、多面函数拟合及三角形网格拟合等）3类[3]，其中：线性拟合局限最大，适用范围最小；平面拟合仅适用于平原等起伏不大的地区；曲面拟合的多项式拟合和多面函数拟合方法，其拟合函数受拟合区域的地形影响而改变[4-5]，三角形网格拟合方法中的DT（delaunay triangulation）网格方法的“三角形中最小角最大”特性最大限度地避免了出现狭长、尖锐的三角形连接，且DT三角剖分的逐点插入法对离散点数据具有容易实现、空间要求不大等优点[6]，较适合已知RTK高程点集的拟合。DT网格拟合方法只保证三角形的最佳形状，并不能明显提高网格区域内的拟合精度。

通过分析高程拟合的评估方法，在检测点已知的情况下，针对三角形网格拟合方法，提出了两种提高外符合精度的方法：第一种是将外符合精度作为限制条件进行三角形网格构建，可在同样数量的顶点下明显地提高精度；第二种是在DT网格顶点中加入计算外符合精度的检测点来进行网格构建，虽增加了顶点数，但效率和精度都明显提高。

1 高程拟合及精度评估

1.1 高程拟合

高程测量中，高程异常ζ为似大地水准面H与椭球面h 之间的差距，即

已知测区的若干水准点，由式（1）求得这些点的高程异常，构造各种数学模型的似大地水准面，然后内插出未知点的高程异常值ζ，进而求出正常高。

1.2 拟合精度评估

对于高程拟合精度的评估，从理论和应用上主要有两种方法：内外符合精度和测量等级标准[7]。

1.2.1 内外符合精度

设V=[v1v2… vn]，vi=ζi-ζi′，则内外符合精度定义为

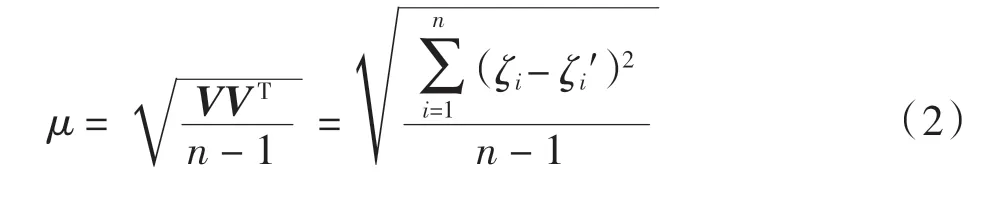
其中：当vi表示在拟合点得到测量高程异常ζi与通过拟合公式计算获得的拟合后的高程异常值ζi′之差时，μ 表示内符合精度，n为参加拟合的已知点个数，可反映拟合点的观测值与拟合值间的精密度；当vi表示在高程检测点得到的高程异常ζi与通过拟合公式计算获得的拟合后的高程异常值ζi′之差时，μ 表示外符合精度，n为参加检测点个数。

内符合精度是反映拟合数据对拟合结果造成的偏差，而外符合精度是反映拟合结果的真实偏差。内、外符合精度从点的统计角度出发，是一种相对意义上的绝对精度评估。内、外符合精度越小，表明拟合模型的精度越高；反之，则表明拟合模型的精度越低。

1.2.2 国家高程控制测量等级

国家高程控制测量等级如表1所示，其中，测区长度L 是所有测量点连线的长度。

一、二等测量需要严格的测量设备，主要应用于地质、水文等勘测工程测量；三、四等水准主要应用于桥梁、道路等一般工程测量。

表1 国家高程控制测量等级Tab.1 National elevation control survey level

2 三角形网格高程拟合方法

通过RTK 定位测量，可得到水准点（拟合点）集Q={Q1，Q2，…，Qn}的厘米级精度的三维数据，基于这些水准点，建立三角形网格。通过三角形顶点（拟合点）的高程数据拟合三角形内各点的高程数据，当网格顶点密度极高时，三角网格的每个三角形可体现该范围内的地形高程，从而得到测区的高程数据。

设高程表示为h=f（x，y），（x，y）∈D，D为点集所在区域，高程网格共有N个三角形，分别记为Ti，i=0，1，…，N-1。称函数

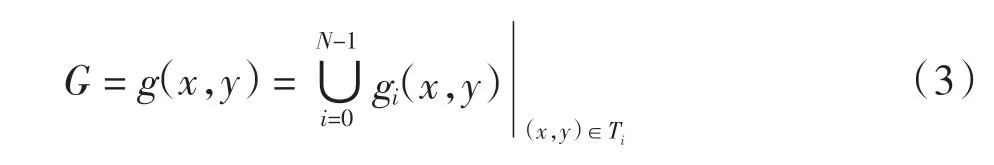
为高程的一个“描述”、“表示”或“逼近”，其中，gi（x，y）是f（x，y）在Ti上的“逼近函数”，且满足某一限制条件。当N 趋近于无限大时，G 趋近于真实高程。

三角形网拟合方法中最常用网格构造方法是DT网格方法[8-9]，具有两个特性：

1）空圆特性 DT三角网格是唯一的（任意4 点不能共圆），在DT三角形网中任一三角形的外接圆范围内不会有其他点存在；

2）最大化最小角特性 在散点集可能形成的三角剖分中，DT三角剖分所形成的三角形的最小角最大。

利用DT网格来对RTK 测量的地形高程进行拟合时，采用逐点插入法，该方法是一种非常适合三维高程数据的三角网格连接方法。其步骤如下：首先，构造一个超级三角形，包含所有散点，放入三角形链表；其次，将点集中的散点依次插入，在三角形链表中找出其外接圆包含插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同被影响的三角形的全部顶点连接起来，从而完成一个点在DT三角形链表中的插入；再根据优化准则对局部新形成的三角形进行优化，将形成的三角形放入DT三角形链表；最后循环插入所有散点，建立三角形。

获得三角形网格连接后，逼近函数g（x，y）可在每个三角形3个顶点确定的平面上进行构造，通过3个顶点的坐标就可以确定的平面方程为

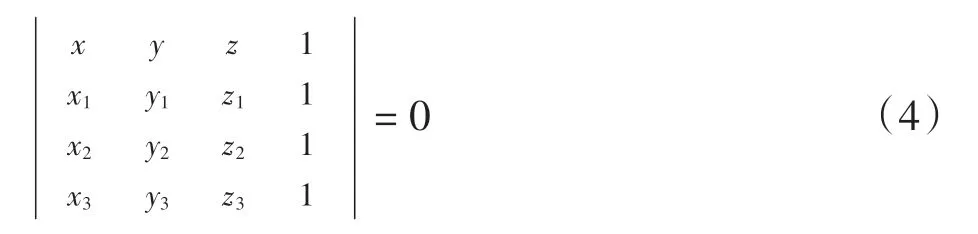
其中：（x1，y1，z1），（x2，y2，z2），（x3，y3，z3）分别表示三角形的3个顶点的坐标。通过式（4）就可得到该平面内各点的拟合高程。

3 基于外符合精度的三角网格方法

DT网格的两个特性保证了其在形状布局上的最佳，但若将其应用于高程拟合上，在水准点较少的情况下（一般情况下为20～30个拟合点），该方法并不能保证其拟合精度达到最佳。在已知检测点的情况下，讨论了两种提高外符合精度的方法。

3.1 基于外符合精度最小准则法

在三角网格中拟合点一定是拟合网格顶点，由式（2）内符合精度概念可知三角网格拟合点处内符合精度为0，在拟合点处已达到最优，不可作为限定条件；而外符合精度是由外部检测点计算得到，反映的是拟合模型的精确度和拟合结果的实际可信度，可作为限定条件。因此，取限制条件C为外符合精度最小准则，即使得式（2）达到最小。

对检测点集P = {P1，P2，…，Pn}，由式（1）ζi= Hihi，ζi′=Hi′-hi′，则最小外符合精度准则为

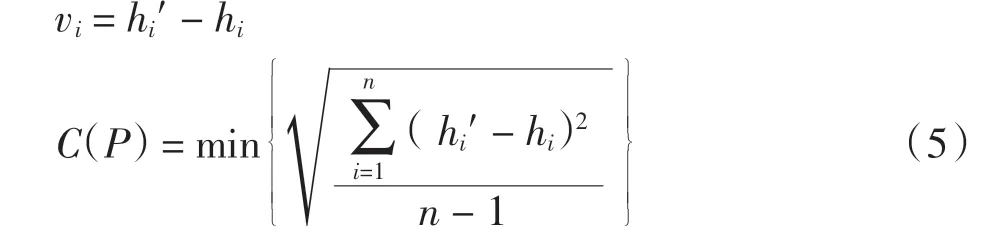
依然按照逐点插入法，建立拟合点的一个初始网格，由式（4）计算检测点集合P={P1，P2，…，Pn}的高程，然后由式（2）计算其外符合精度，遍历所有三角网格连接链表，选取使C（P）最小的三角形作为网格中的三角形Ti，最终找到最小外符合精度的整体三角形网格。在20个拟合点、5个检测点的情况下分别进行DT网格法及基于外符合精度的三角形网格法处理，最终的网格连接结果分别如图1和图2所示。

由图1和图2 对比可看到，图2的三角网格并不再是规则的DT网格，其中，2、10、13、15 这些点的三角形连接发生了明显变化，这种变化是由外符合精度决定的，变化后的三角形的外符合精度更小，符合添加的精度准则。

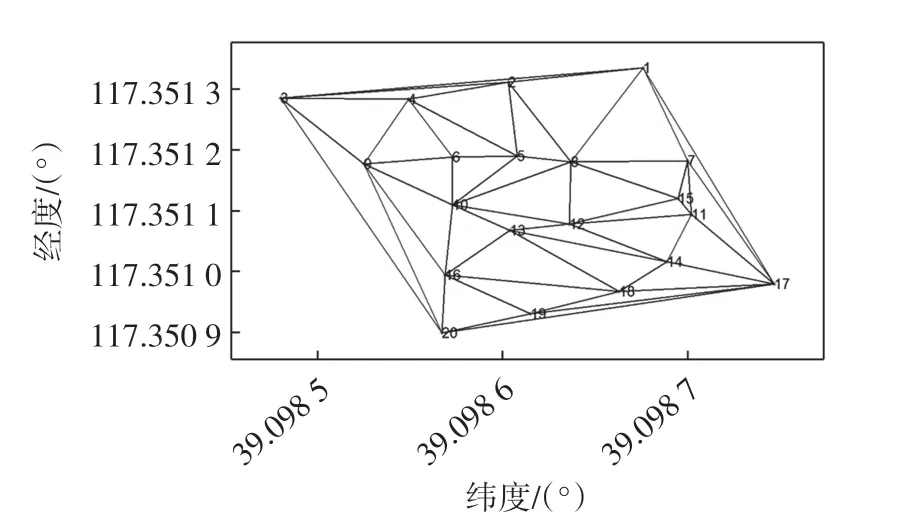
图1 DT网格Fig.1 DT mesh

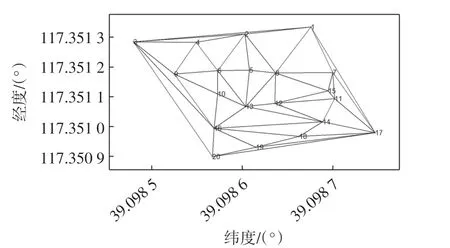
图2 基于外符合精度的三角形网格Fig.2 Triangular mesh based on external coincidence accuracy

3.2 加入检测点的DT网格拟合

实际上，由式（2）可见，当所有检测点均为拟合点时，高程拟合的外符合精度直接达到最优值0，因此为了提高DT网格的拟合精度，在检测点数据已知且不可进行改变的情况下，将检测点加入到拟合点集中，把拟合点和检测点均看作网格顶点进行DT网格的构建，这时拟合结果的外符合精度必然为0。从理论上讲：一方面，检测点加入到拟合点集中相当于扩充了原始的拟合点集，随着拟合点或网格顶点的增多，拟合平面的精度自然要高于仅采用拟合点进行拟合的DT网格；另一方面，由于检测点参与DT网格构建，因此当仍用这些检测点进行检测时，外符合精度值自然为0。含有20个拟合点和5个检测点的DT网格如图3所示。

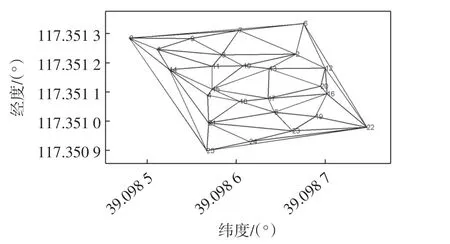
图3 加入检测点的DT网格Fig.3 DT mesh with detection points

4 实验结果分析

4.1 数据处理

实验室采用司南基站M-300和移动站M-600 接收机进行RTK 测量数据获取，在应用RTK 测量过程中由于环境条件、仪器等原因会使观测数据出现粗差，数据处理中首要任务是检验并剔除存在粗差的观测值，否则会导致高程异常模型的失真或扭曲，极大地影响拟合精度。

通常在高程拟合中已知点不会太多，通常以标准化残差ζi进行β 检验[10]，即

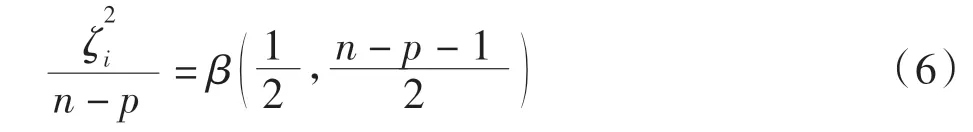
其中：n为观测组数；p为未知参数个数；β（a，b）是β 分布。取显著水平α，当β ＞β(α)时，认为此残差是粗差，并剔除，可有效提高RTK 测量数据的可靠性。

4.2 实验分析

采用粗差剔除后的数据，均匀选取20个数据作为拟合点，分别进行平面、二次曲面、三次曲面、四次曲面、多面函数等常规拟合方法，DT网格方法，基于外符合精度的三角形网格（方法1）和加入检测点的DT网格（方法2）进行拟合，并对其结果进行比较和精度分析。拟合后的高程对比结果，如表2所示。

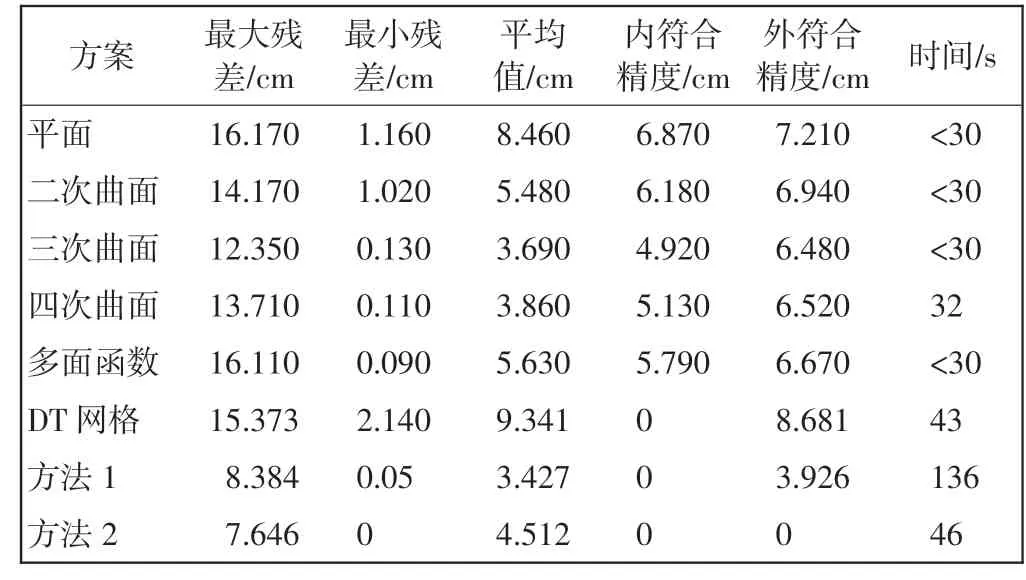
表2 曲面拟合高程异常残差结果Tab.2 Curved surface fitting results of elevation anomaly residuals

表2 中残差值是指拟合平面上高程和实际曲面高程的差值。对于三角网格方法（DT网格法、方法1及方法2），由于三角网格拟合顶点处内符合精度为0，因此，仅比较网格的外符合精度值。由表2 可看出，常规平面、曲面方法较DT网格在高程拟合的精度方面有一定优势，但方法加外符合精度最小这一约束条件后，三角形网格方法精度的提高尤为明显，提高了约121%的外符合精度值，且优于其他常规高程拟合方法。外符合精度一定程度上反映了拟合模型的可行性，通过这种方法可以有效地改进DT网格拟合在精度上不足，从而提高拟合结果。此外，方法2 把检测点也当作拟合点（网格顶点），可看出其平均残差相比DT网格有明显提高，又由于网格顶点一定在拟合曲面上，其内外符合精度均为0。

方法1、2 计算的测区长度大于6 km，其四等水准限差为4.8 cm，基于外符合精度的三角网格方法拟合结果满足国家四等水准测量等级以上。

从时间效率来看：三角网格拟合方法耗时均长于常规拟合方法；方法1 耗时相对较长，是DT网格的近3 倍，实际拟合过程中，通常使用20～30个拟合点，因此方法1的时间效率可接受；方法2 在20个网格顶点的基础上又加入5个检测点作为顶点，属于成熟DT网格方法，在精度提高的同时时间效率变化不大。

5 结语

结合RTK 测量的特点，考虑到其高程上存在的不足，基于外符合精度，提出了两种三角形网格拟合方案。实验结果表明：该三角形网格方法在已知检测点的情况下可显著提高RTK高程拟合的精度，精度高于曲面拟合和DT网格拟合方法，能较好地拟合出实际高程。该方法对民航飞行程序设计、机场建设等工程应用的高程测量有一定的应用价值。