考虑低载荷强化效应的汽车转向节疲劳分析*
董国疆,杜 飞,王 威,郎玉玲
(1.燕山大学,河北省特种运载装备重点实验室,秦皇岛 066004; 2.中信戴卡股份有限公司工程仿真中心,秦皇岛 066004)
前言
汽车行业发展至今,世界各大汽车厂商对于汽车的研发已经形成了属于自己的一套独有的研发体系,而耐久性试验是其中最重要的验证环节[1]之一。大量的耐久性试验发现,结构件的疲劳寿命通常高于理论或仿真预估的疲劳寿命,究其原因主要是在估算结构件寿命时往往只考虑高于疲劳极限的载荷,而忽略了低于疲劳极限的载荷[2]。据统计显示,耐久性试验载荷谱中80%的随机载荷均为低于疲劳极限的载荷,然而这些小载荷会对构件产生不同程度的强化作用[3-4],即低载荷强化效应,最早是被英国的GOUGH发现并验证的。而后诸多学者对大量的金属及合金材料进行了低载荷强化效果实验,揭示其机理为小载荷引起金属基体中位错增殖和移动行为,大量位错在晶界上聚集而形成钉扎作用,使位错再运动和滑移阻力增加,导致金属屈服点上升且疲劳强度提高,产生强化效应[5]。另有研究表明金属材料的低载荷强化特性受所施加载荷大小和载荷循环次数有关,分别存在最佳强化载荷和最佳强化次数[6]。国内学者对低载荷强化效应在机械构件上的应用开展了大量研究,卢曦等[7]研究低幅载荷对某轿车倒挡圆柱齿轮的影响,发现疲劳强度提高了3.97%,疲劳寿命提高了109%;郑松林等[8]探索低幅锻炼载荷对汽车传动轴的影响,分别用低载扭矩作为锻炼载荷并循环加载,再以301 N·m大扭矩载荷进行剩余疲劳强度试验,发现在经99 N·m扭矩锻炼20万次下的传动轴疲劳强度提高33%;梁凌宇[9]选取292~351 MPa低应力对结构钢进行低载荷强化试验,发现经312 MPa低应力幅加载30万次后再用520 MPa高应力加载,应力幅为520 MPa的疲劳寿命提高了62%。上述研究表明,大多金属构件对低载荷强化具有较强的敏感性,对构件进行疲劳耐久性能研究应充分考虑低载荷强化以期提高疲劳寿命预估精度。
底盘构件在汽车行驶过程中承载工况最为复杂,极易产生疲劳损伤。但是大多工况的载荷谱中均含有大量幅值低于材料疲劳极限的低幅载荷,在构件开发中往往将其忽略,并未考虑低载荷强化效应,使得对构件的寿命预估偏于保守,耐久性设计裕度较大。因此,本文中基于上述研究成果,以某SUV前转向节为研究对象,实测并采用试验场耐久性测试强化道路的应变谱,实测并应用更为复杂的试验场强化道路载荷谱,将其处理、编辑、转化、外推和修正分级,获取10级等效应力谱;以此分别采用Miner理论和低载强化理论开展转向节疲劳寿命分析,进一步讨论和验证低载强化效应对疲劳寿命的影响机制,为实际汽车底盘构件疲劳寿命估计与轻量化设计提供新的参考。
1 转向节强化路应变信号采集
1.1 转向节应变测试方案设计
疲劳寿命预估的三要素为材料疲劳性能、实测载荷谱和疲劳累积损伤法则。实测载荷谱是疲劳寿命预估的基础数据,但并不是构件上任一位置的应变谱都能够用于疲劳寿命预估。疲劳损伤危险点是构件中最早发生疲劳破坏的起点,工程上常以该点疲劳失效时间来评价构件本身的疲劳寿命。本文中通过试验与仿真相结合的方法找出转向节疲劳损伤危险点,并作为耐久性道路实车测试的应变信号监测点。通过室内振动台架测试样车垂向跳动工况轮心六分力信号;建立转向节有限元仿真模型并通过模态试验验证;以实测轮心六分力为动载激励开展转向节疲劳损伤仿真,获取疲劳损伤危险点,进而确定转向节路测应变监测点。
(1)振动台架实车测试。试验车型选用某品牌 SUV,整车质量1 531 kg,轴距2 680 mm,轮距3 574 mm,前悬麦弗逊,后悬双横臂。振动台采用Premax MIMO振动控制系统,激振器类型HSV-75.1,频率范围 0.1~300 Hz,最 大正弦推力50 kN,如图1所示。试验采用LW12.8六分力传感器和MSC测试系统,六分力信息如表1所示。设计振动台测试工况如表2所示,测试获得多种工况下轮心六分力,图2为表2所示工况5采集的部分六分力。

图1 室内振动台与轮心六分力仪
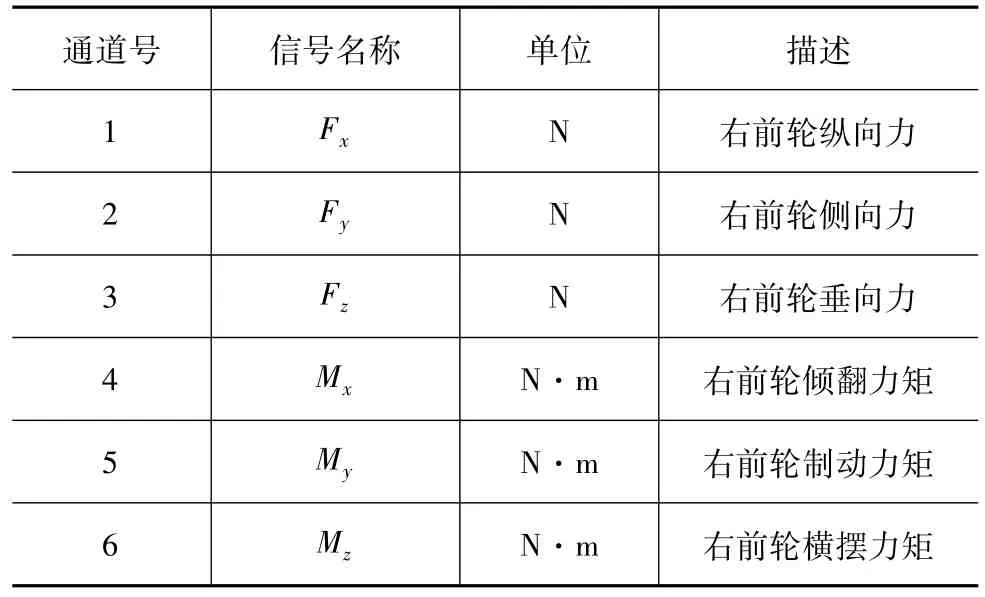
表1 试验车辆轮心六分力通道布置
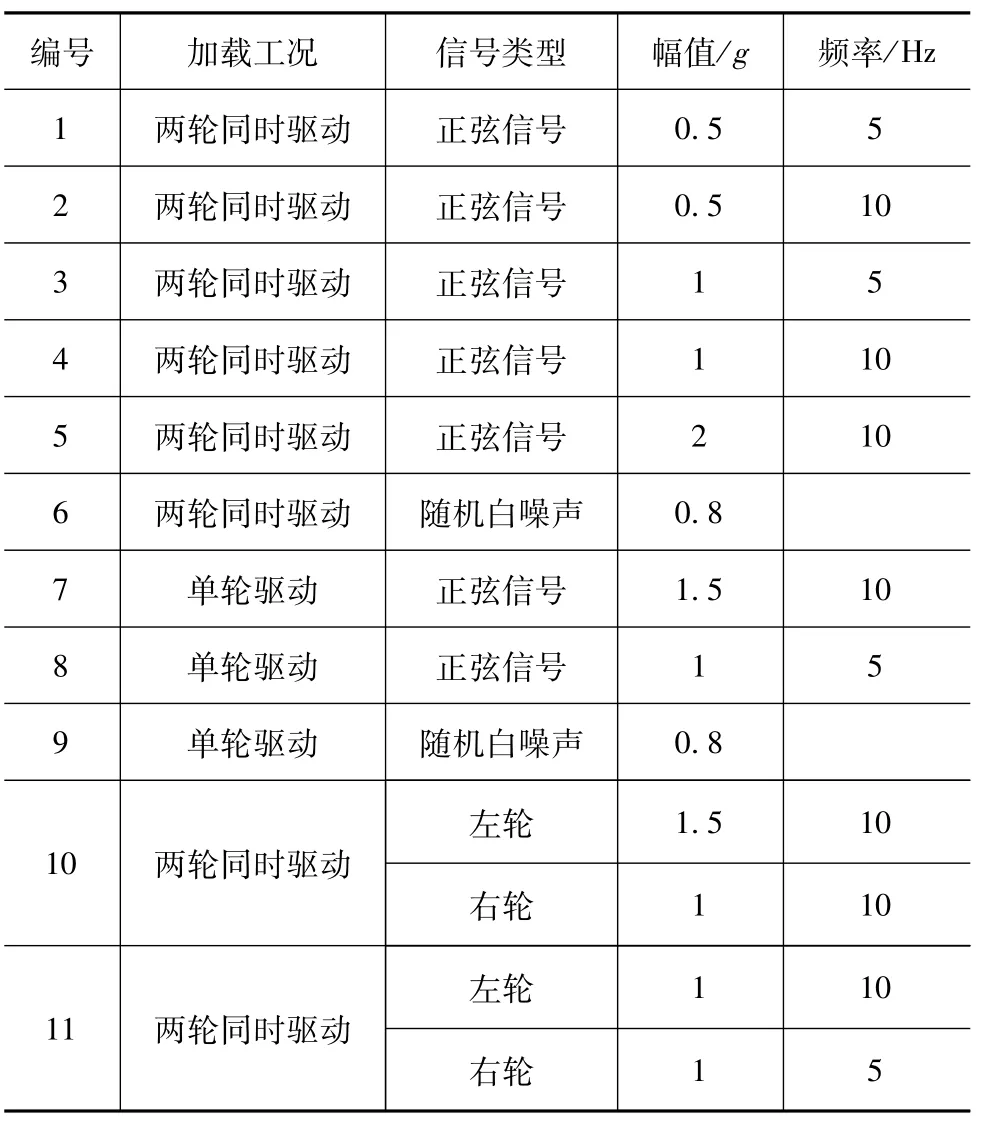
表2 室内台架实车振动加载工况表
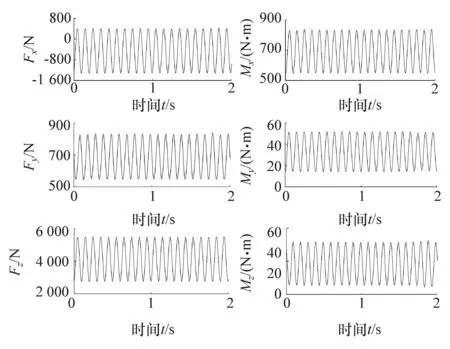
图2 台架振动工况5实测左前轮心六分力
(2)建立转向节有限元模型。转向节几何模型通过3D扫描CATIA逆向建模获取,导入Hypermesh划分网格并设置相关参数,建立转向节有限元仿真模型。应用模态实验对模型进行验证,采用力锤激励法对转向节进行自由模态试验,使用DHDAS动态信号采集仪采集响应点的加速度信号,根据激励与响应之间的传递函数识别转向节模态参数,得到测试点固有频率的平均值,并与仿真值对比如表3所示。试验与仿真固有频率相对误差均在7%以内,验证了转向节有限元模型的准确性[10]。根据转向节装配关系设置模型主节点约束条件,对转向节轴心施加振动台架实测各工况轮心六分力载荷谱,调用模态综合法,设置输出模态中性文件的卡片,利用patran求解器得到疲劳仿真软件Ncode所需的OP2文件。
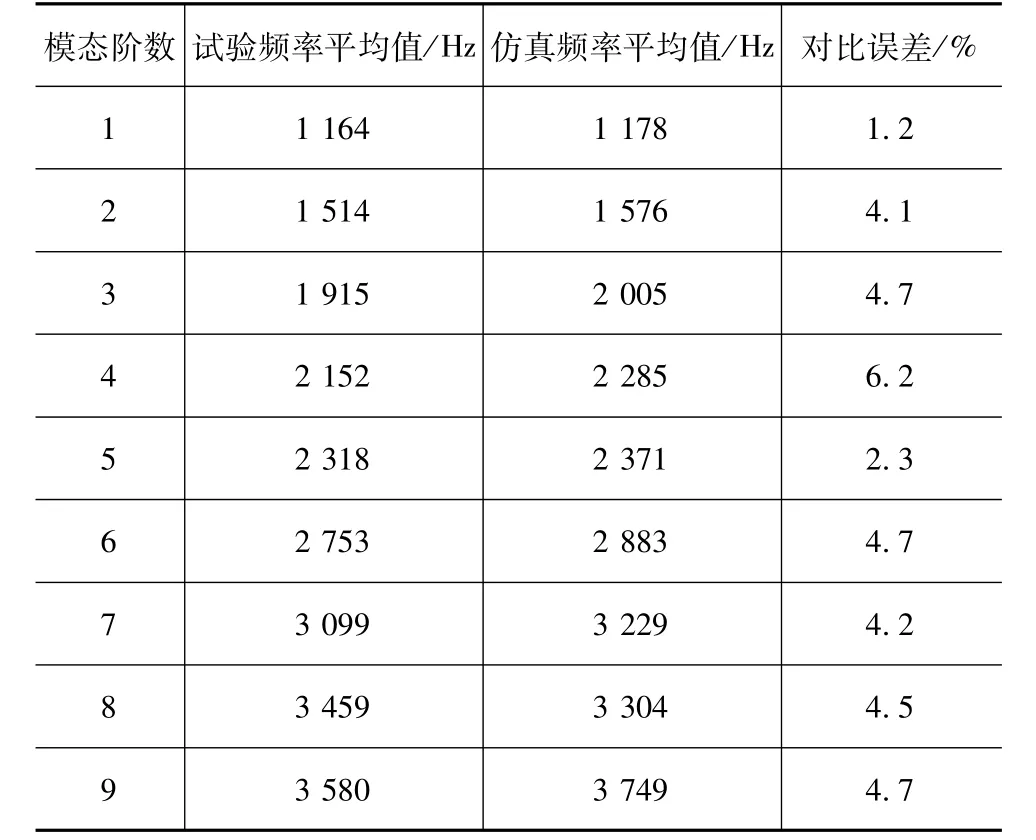
表3 转向节自由模态频率试验与仿真对比
(3)转向节动载损伤仿真。动载仿真在Ncode软件Designlife模块中进行,运用线性疲劳损伤累计理论计算各种工况下转向节损伤累计状况(如图3所示),观察累积损伤云图发现各工况下损伤累积最危险均指向转向节与减振器滑柱连接点处,由此确定实车路试转向节应变监测点位置。设计应变花传感器和采集方案,并布置安装温度补偿线路(如图3所示),以减小在测试过程中应变花传感器敏感栅电阻丝温度变化引起的信号波动和误差。
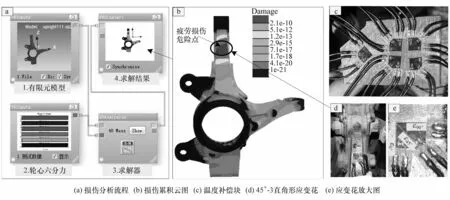
图3 转向节动载损伤仿真流程示意图与应变监测点选取
1.2 应变谱采集及预处理
转向节应变谱采集选取北京通州试车场疲劳耐久性测试强化道路(如表4所示)。试验车配重方案为:驾驶座驾驶员80 kg,副驾驶座乘员75 kg,后排座两个70 kg乘员,整车质量为1 831 kg,前后轮质量分配系数为1.1。路采试验由试车员按照《北京通州交通部试验场的疲劳耐久试验规范》进行,信号采集频率设定为1 000 Hz,每种强化道路工况采集5组试验数据。实车采集了强化道路轮心六分力信号,悬架、车身的位移和加速度信号和转向节应变监测点(即疲劳损伤危险点)信号,如图4所示,图中序号对应强化道路各种路型。
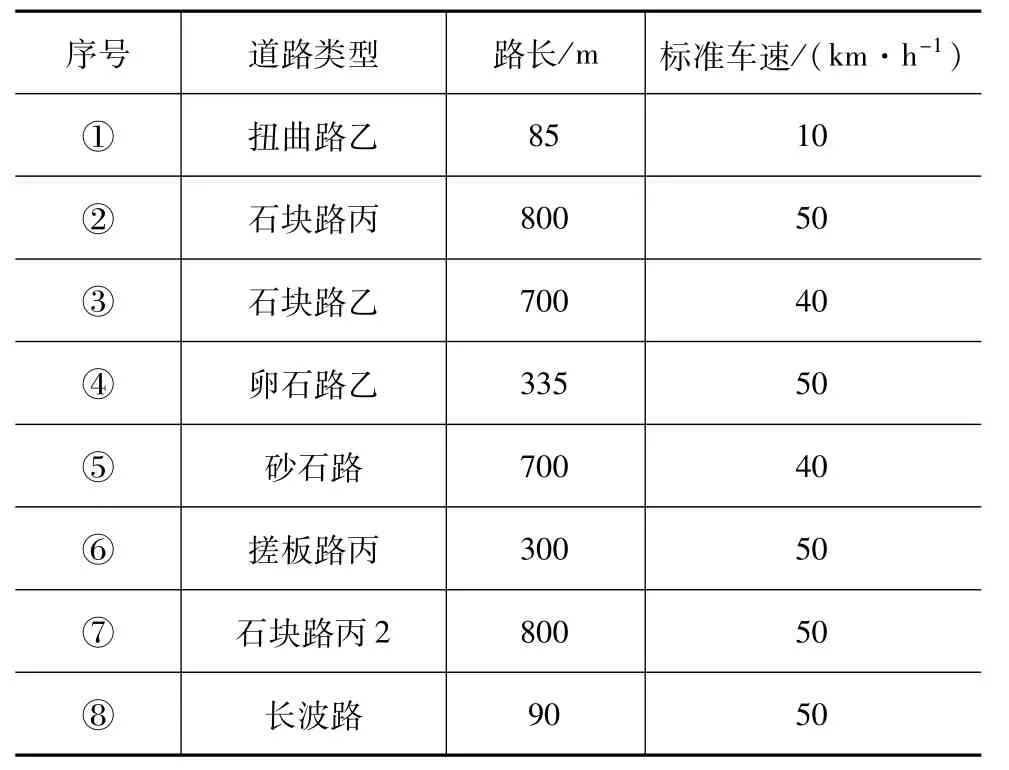
表4 试验场强化道路数采信息表
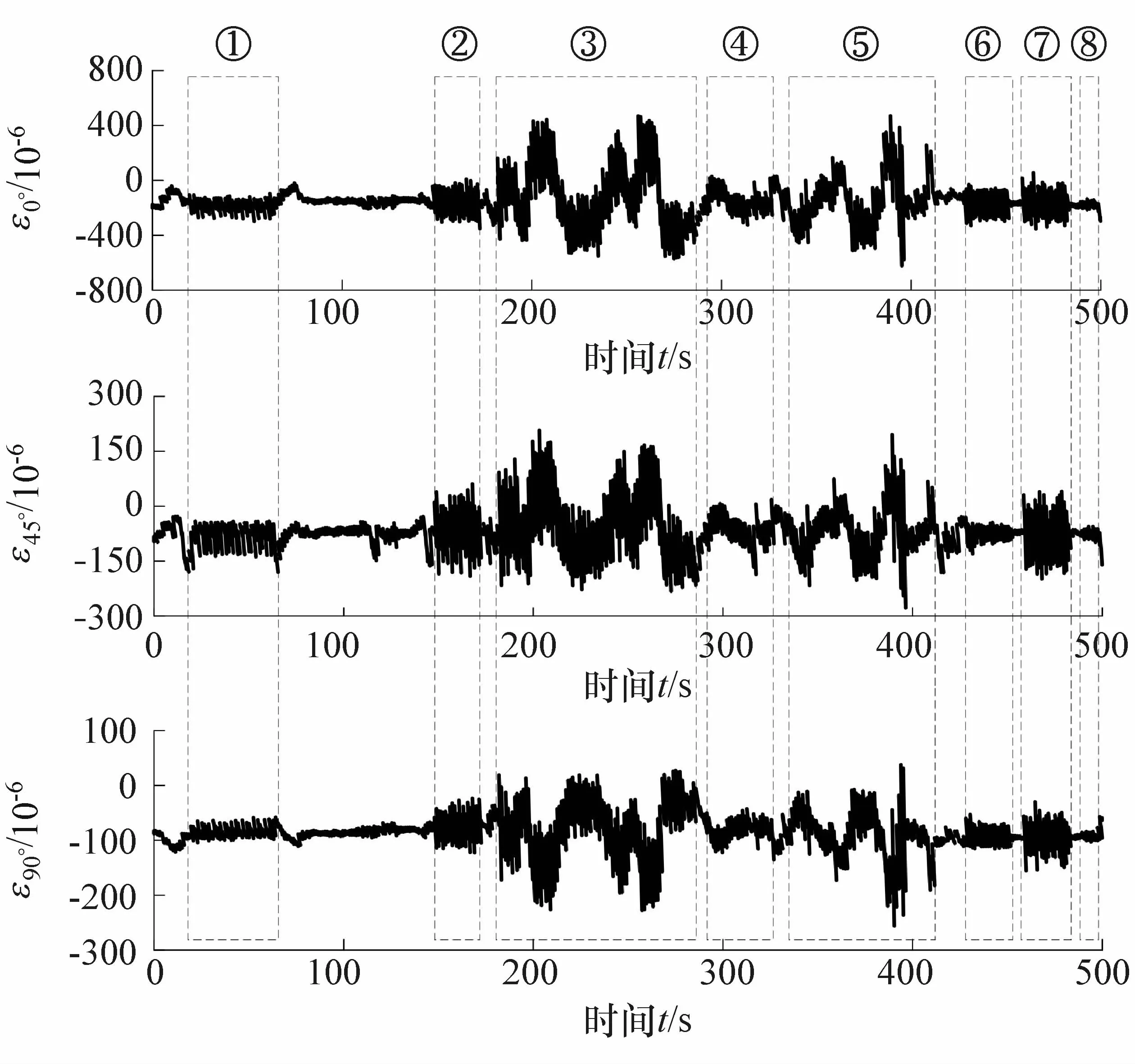
图4 实车路试转向节监测点应变信号
实测转向节监测点应变信号预处理主要包括去漂移、去毛刺和去除奇异值等3项工作。测试过程中虽然采取了温度补偿措施,但实测应变时域信号依然产生了异常偏移,漂移影响贯穿整个测试时段。去除漂移的方法主要有两种:一是求解实测信号平均值,用原始信号减去平均值即可得到去除漂移信号;二是通过带通滤波,设置合理的频带宽度对信号进行滤波处理。可通过功率谱密度PSD(如图5所示)识别到该应变信号的频率范围:应变监测点ε0°和 ε90°均在 0~50 Hz;ε45°在 0~30 Hz。据此对实测应变信号进行相应频率范围的带通滤波去除漂移趋势项。
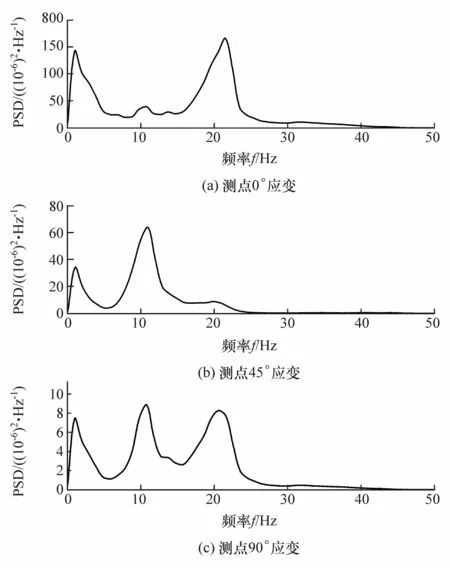
图5 转向节应变监测点应变信号功率谱密度PSD
实测信号由于测试系统的电流和电磁干扰,导致测点信号产生毛刺,可采用高通滤波将其去除,频率定为1 Hz,过滤0~1 Hz的噪声信号。奇异值探测可应用雨流技术统计,通过俯视图观测散点位置而去除离散值;也可采用微分梯度法对奇异值进行探测,应用Ncode软件spike detection模块设置Differential检测方法处理应变信号。
本文中拟采用名义应力法预估转向节疲劳寿命,须将实测转向节表面应变谱转换为等效应变谱,再依据材料弹性力学性能将其转化为等效应力谱。按照45°-3直角形应变花等效应变合成方法将实测监测点 ε0°、ε45°和 ε90°应变谱转化为等效应变谱。
同时,反复实测是为了确保试验数据的可靠性,即使是同一路段、同一驾驶员操作,所采集的信号也会存在一定的差异。为了更加精确地获取原始道路信息,需要对实测信号进行筛选。标准差可用来衡量随机信号的离散程度,标准差越小的信号越稳定。因此,本文中采用最小标准差法[11]对采集的5组应变监测点等效应变信号进行重组,分别对每段强化道路的应变时间历程进行标准差统计,如表5所示。通过对表5的对比分析,把每段强化道路中标准差最小的载荷谱进行重新组合,得到的应变时间历程如图6所示。
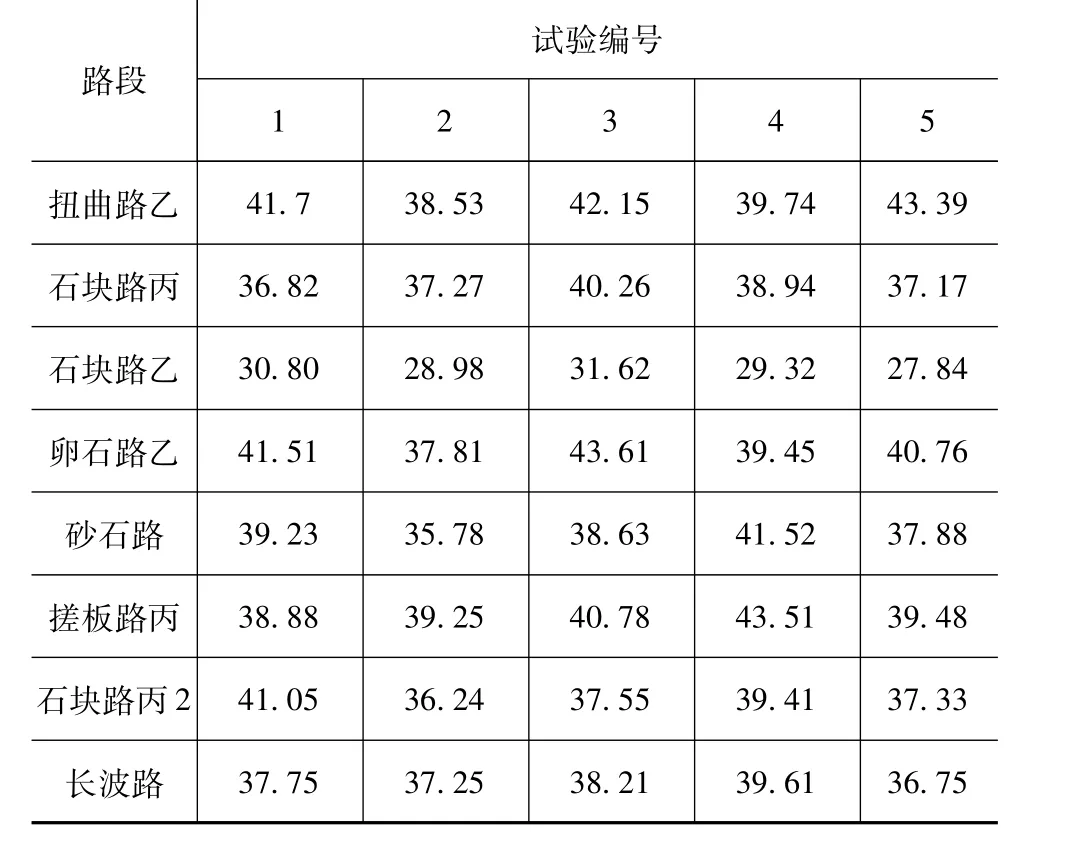
表5 强化路转向节监测点等效应变信号标准差统计表
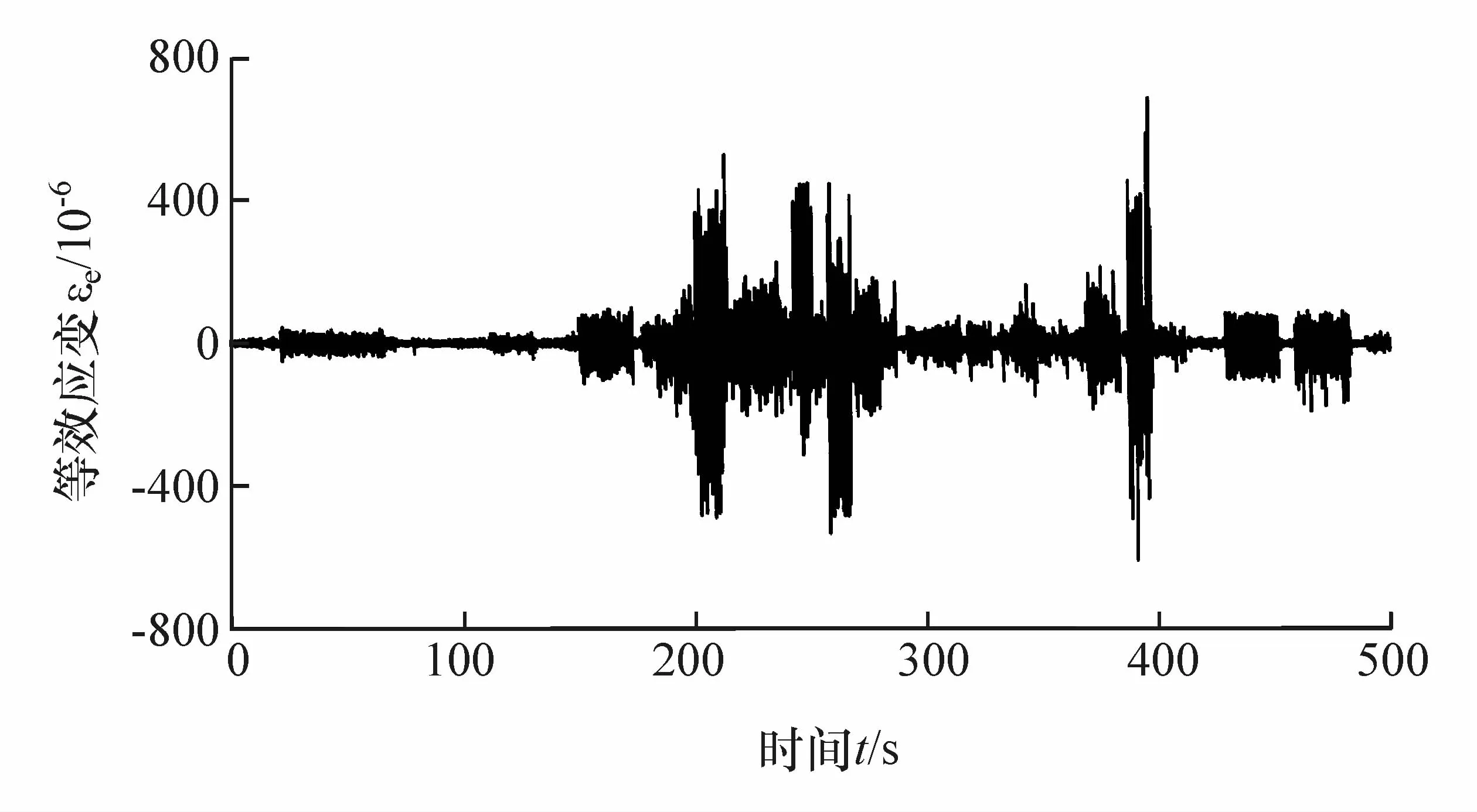
图6 转向节监测点等效应变重组信号
2 转向节载荷谱时域加速编辑
低载强化效应考虑的是应力载荷对构件疲劳强度的影响,因此需要把应变载荷转化为应力载荷。转向节服役期间,通常承受的循环应力低于材料的屈服极限,疲劳破坏前经历的循环次数大于105次,因此转向节的疲劳类型属于高周疲劳,且承载变形均在弹性范围以内,应力与应变关系为线性。试验车辆转向节材料为球墨铸铁QT500-7,其弹性模量为173 GPa,根据弹性范围的应力与应变关系,可将转向节监测点等效应变重组谱转化为等效应力谱,如图7所示。
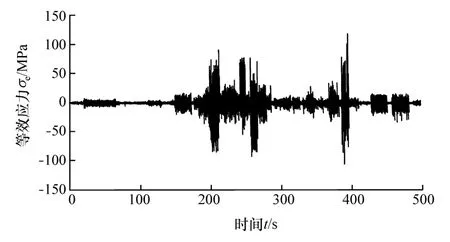
图7 转向节监测点对应转化的等效应力谱
由于实测强化道路的应变信号包含大量的连接道路等无用信息,因此需要对转向节监测点等效应力谱进行加速编辑。应力谱加速编辑可以从幅值域、频域和时域3方面进行,但是从幅值域和频域两方面加速编辑易丢失加载循序、信号相位对应关系和原始谱频率特性,无法重现真实载荷 时间历程。为此,本文中采用时域信号加速编辑等效应力谱,删除对转向节即无损伤作用又无强化作用的无效载荷。载荷谱加速编辑重点在于确定无效载荷的删除阈值[12],研究显示删除阈值不大于最大载荷幅值的13%,试样疲劳寿命无显著差异,但删除幅度接近最大载荷幅值20%时,疲劳寿命将达到“谷”点[13]。本文中采用时域范畴的伪损伤保留法[14]进行等效应力谱加速编辑。设置伪损伤保留比例为99%,初步给定最大载荷幅值10%作为删除阈值,应用Ncode数据处理模块对应力谱加速编辑,与原始谱伪损伤量对比,若加速谱伪损伤保留比例不满足设定要求,则调整删除阈值返回运算,最终确定删除阈值为最大载荷幅值的12.8%,获取的等效应力加速谱如图8所示。等效应力谱加速编辑后,时域坐标从498 s缩短至188 s,压缩比为37.8%。
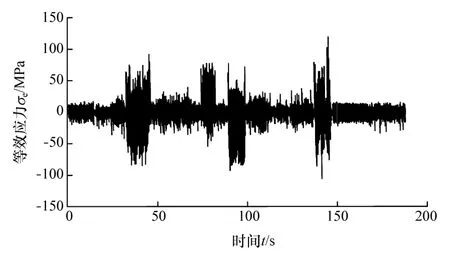
图8 转向节监测点等效应力的加速谱
为确保加速编辑前后等效应力谱的载荷特征相同,本文中分别从幅值域和频率域进行对比分析。幅值域分析载荷谱穿级计数曲线比对显示(如图9所示),等效应力加速谱高循环次数的小幅值载荷被删除,循环次数低于2 500的较大幅值载荷曲线与原曲线基本吻合。频率域分析主要依据载荷谱功率谱密度(如图10所示),功率谱密度反映时间信号的功率随频率分布的关系。对比显示,等效应力谱加速编辑前后的频率特征近似,等效应力加速谱的功率谱密度较原信号整体上移,说明加速编辑后在各频率上的平均能量较原始谱提高,原因在于加速编辑删除了各频率中分布的小载荷,使加速谱对应频率的平均能量升高。
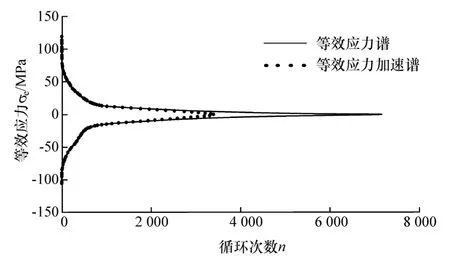
图9 加速编辑前后等效应力谱穿级计数曲线
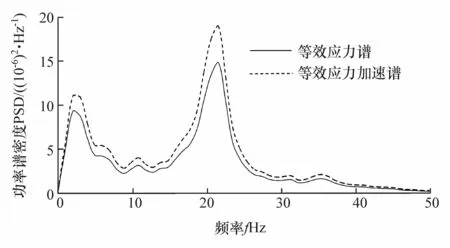
图10 加速编辑前后等效应力谱功率谱密度曲线
3 考虑低幅载荷的疲劳损伤分析
考虑低载强化效应的转向节疲劳寿命预判,需将前文中整理的组合强化路单次循环的等效应力加速谱进行雨流计数统计,将雨流矩阵根据试验场疲劳耐久性规范外推为一个完整周期的载荷谱块,并以此谱块循环加载次数作为转向节疲劳寿命的评判量度。应用Goodman公式对外推谱块进行平均应力修正得到等效0均值应力谱,按照8级载荷谱编制方法[15]将等效0均值应力谱编制为10级应力谱,根据材料的低载强化特性并结合实际损伤过程中疲劳极限附近载荷也会对构件产生损伤这一现象,将10级应力谱划分为无效载荷、强化载荷和损伤载荷。有研究表明[16],金属材料强化载荷范围一般在[0.65σ-1b,0.95σ-1b],σ-1b为构件疲劳极限。考虑强化载荷对材料疲劳特性的强化效应修正材料S-N曲线,并基于Miner准则进行转向节疲劳损伤分析,流程如图11所示。
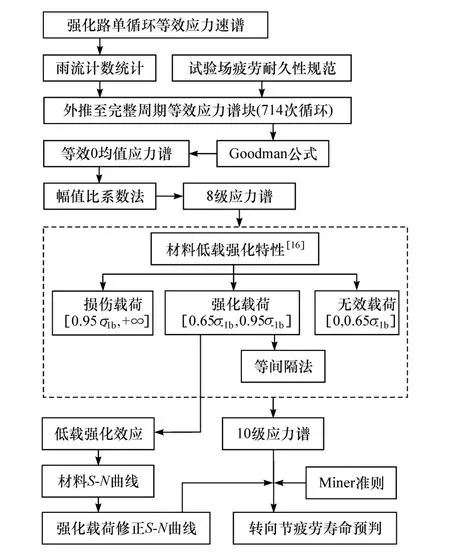
图11 考虑低载荷强化的转向节疲劳寿命预判流程图
3.1 载荷谱雨流计数及外推
雨流计数法依据材料应力应变行为记录材料的应力应变循环中的所有迟滞回环,而迟滞回环是疲劳计算的基础,在疲劳损伤研究领域应用广泛[17]。雨流计数法把经过峰谷值检测的实测载荷历程数据以离散载荷循环的形式表达,记录随机载荷的均值和幅值。应用雨流计数法对等效应力加速谱进行统计计数并外推至714次循环,达到试验场疲劳耐久测试规定当量,得到雨流柱状图和幅值 频次曲线,如图12~图14所示。
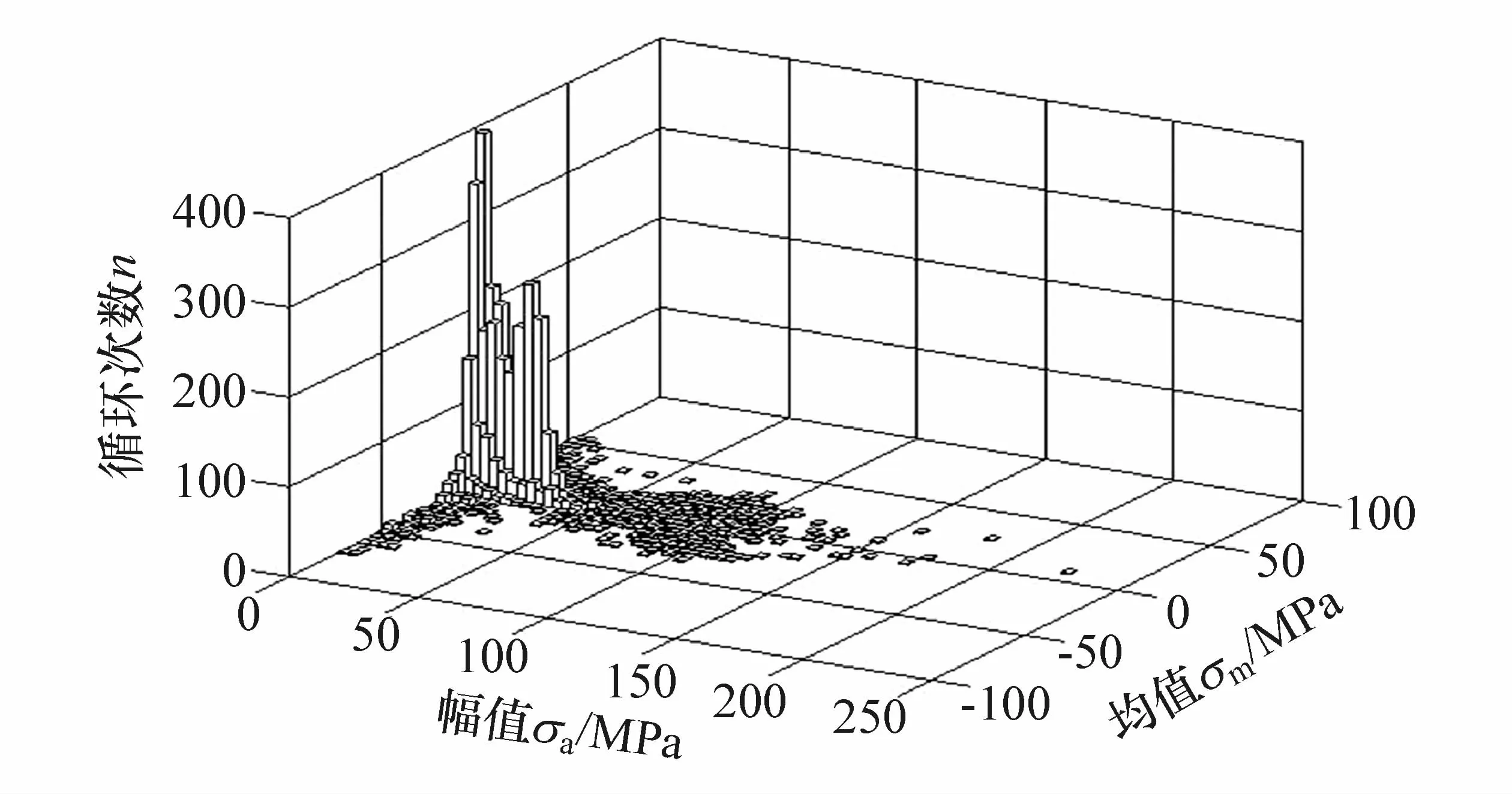
图12 等效应力加速谱外推前雨流柱状图
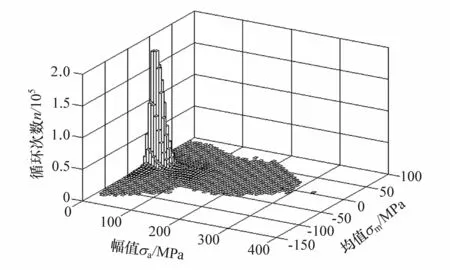
图13 等效应力加速谱外推后雨流柱状图
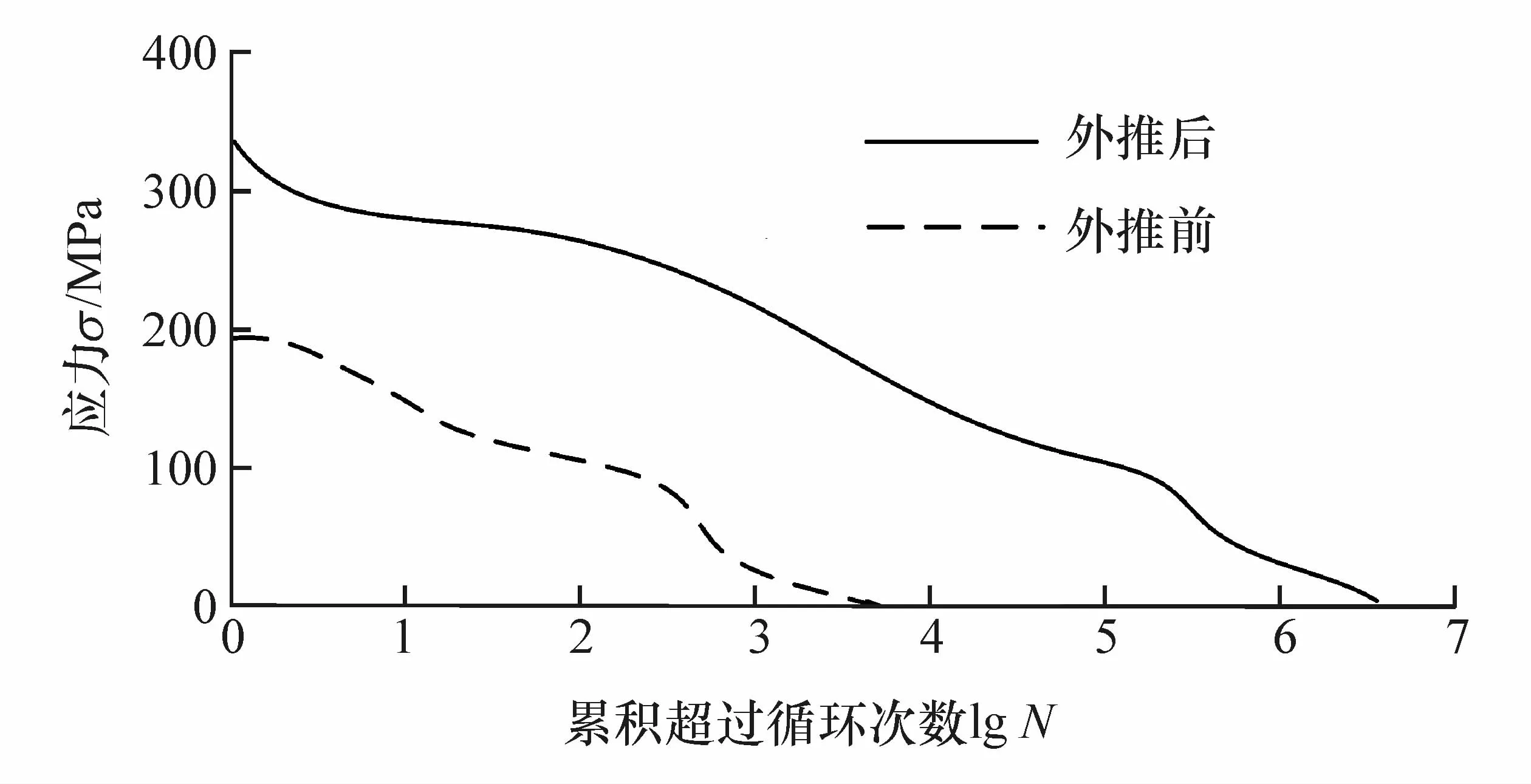
图14 等效应力加速谱外推前后幅值 频次曲线
由于低载强化试验是通过恒幅对称循环载荷(应力比为-1)加载得到的,应力比为载荷循环加载时最小应力与最大应力之比。因此,需要把等效应力加速谱修正为平均应力为0(应力比为-1)的应力谱,即把既有均值和幅值的二维应力谱转化为均值为0的一维应力谱,采用Goodman公式修正,等效0均值应力谱转化式如下:

式中:Sa为应力幅值,MPa;Sa0为等效0均值应力,MPa;Sm为应力均值,MPa;SUTS为强度极限,MPa。
通过修正得到的等效0均值应力幅值密度较大,需要对其进行分级。德国工程师Gassner提出将载荷谱幅值分为8级,并且Conover发现将载荷谱分为8级可以很精确地反映其疲劳效应,现已应用于工程实际[18-19]。各级载荷划分可以按照等间隔法和幅值比系数法,本文中应用幅值比系数法[20]进行划分,幅值比系数分别取:1,0.95,0.85,0.725,0.575,0.425,0.275和 0.125。考虑材料的强化区间[0.65σ-1b,0.95σ-1b]对应幅值比系数为[0.271,0.397],为了更精确地考虑载荷强化作用,按照等间隔法将强化区间划分为两个等级,分别为0.75σ-1b和0.85σ-1b,对应的幅值比系数为 0.313和 0.355,得到10级应力谱。
3.2 考虑低幅载荷寿命预估
样车前轮转向节所用材料为QT500-7型球墨铸铁,其抗拉强度 σb=625 MPa,屈服极限 σs=475 MPa,伸长率大于7%,疲劳极限(107次循环)为

式中:载荷系数 CL为0.84;表面质量系数 CS为0.78;尺寸系数 CD为 0.9;可靠性水平系数 CR为0.8;疲劳缺口系数 Kf为 1。代入参数,可得 σ-1b=124 MPa,σ1000=425 MPa。
对球墨铸铁圆棒进行低载荷强化试验及数据拟合,得到强化载荷S、强化载荷循环次数n和疲劳强度增比r的低载强化三维曲面,如图15所示。可知球墨铸铁的最佳强化次数nbest为2×105次,从低载强化三维曲面上抽取对应曲线,并采用多项式拟合曲线(见图16),强化载荷S与疲劳强度增比rm(n=nbest)拟合式为
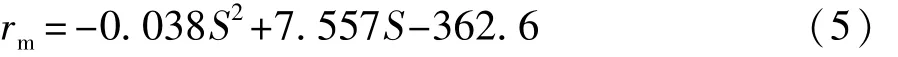
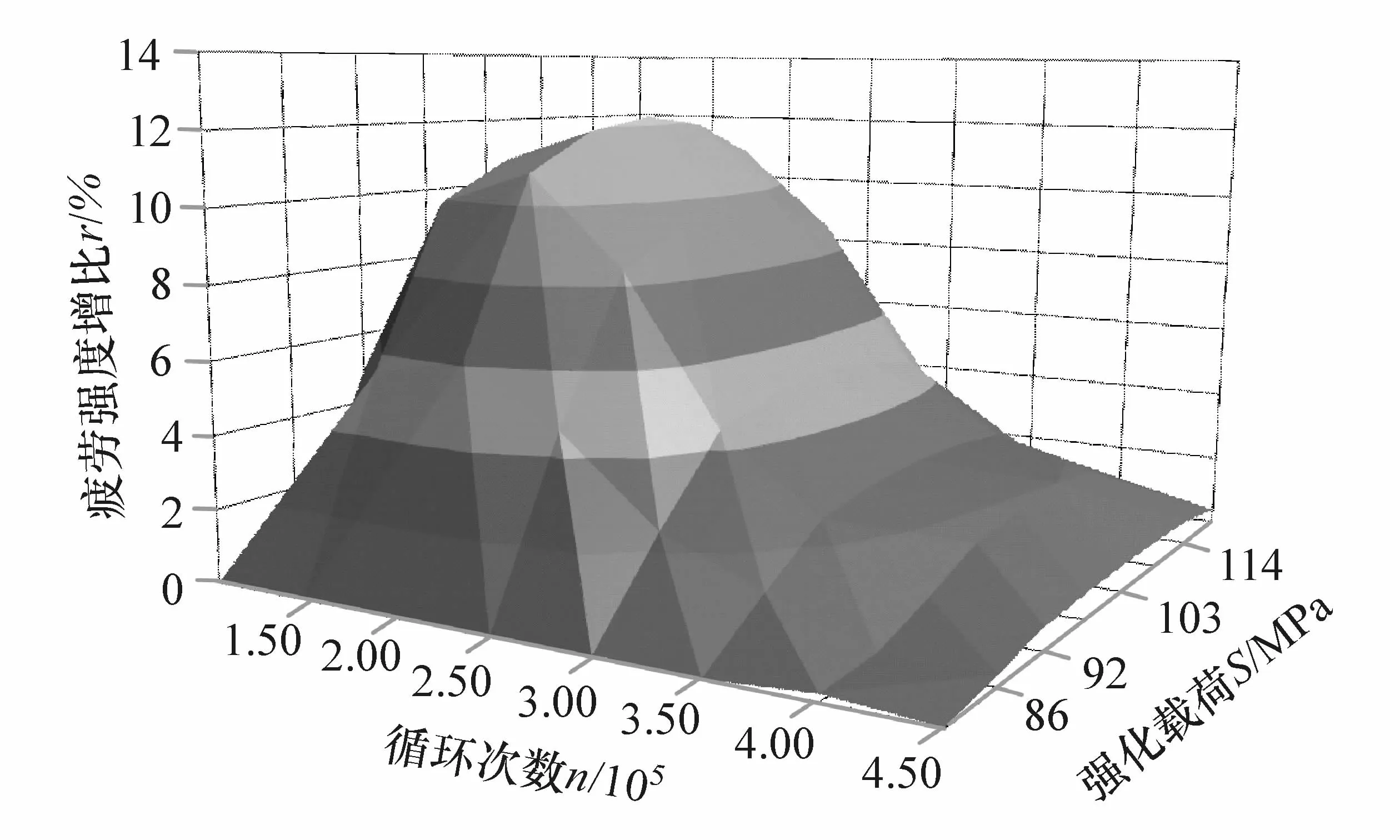
图15 球墨铸铁低载强化三维空间曲面
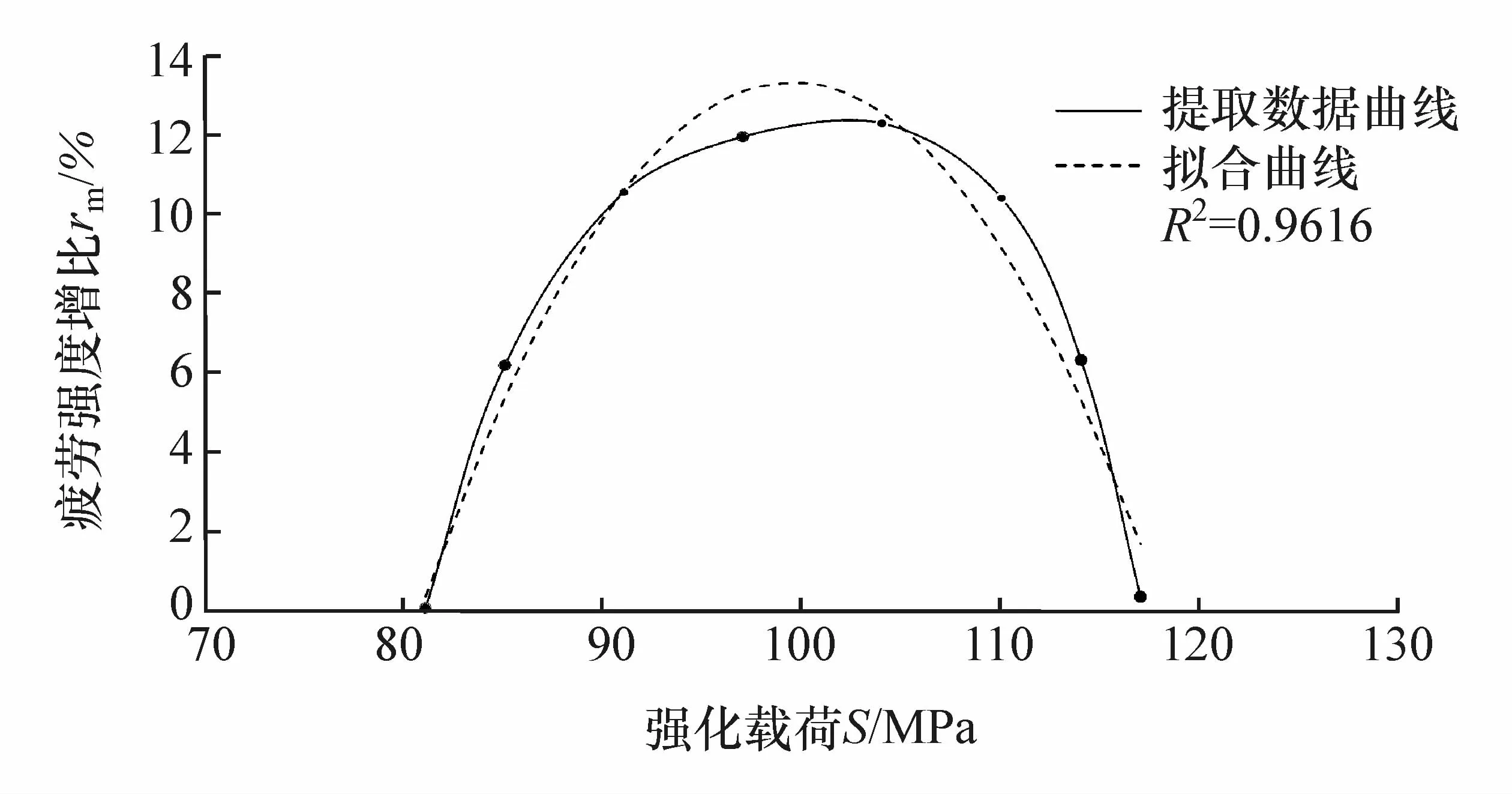
图16 最佳强化次数下疲劳强度增比与强化载荷曲线
10级应力谱中强化区间的循环次数小于最佳强化次数,如表6所示,可将强化载荷循环次数ni(i为强化载荷级数)与每级强化载荷下疲劳强度增比ri简化线性关系为

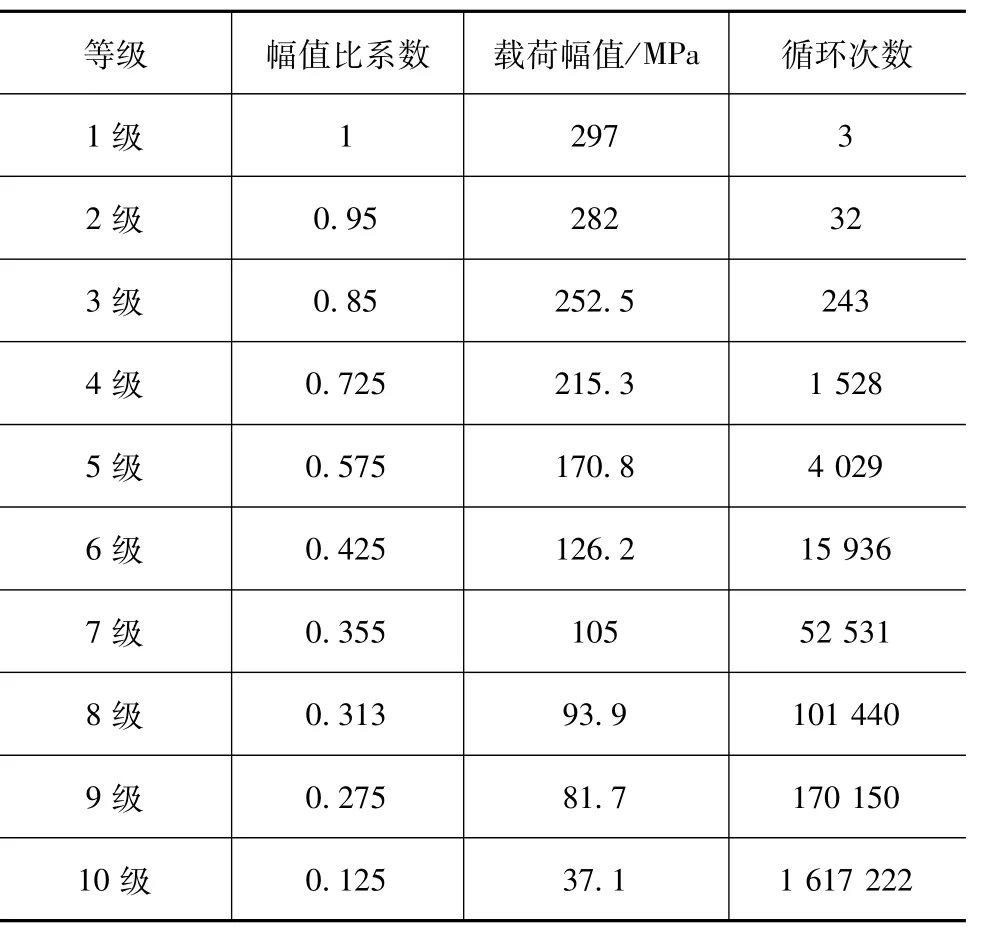
表6 10级应力谱分级
根据强化载荷范围[0.65σ-1b,0.95σ-1b],即[80.6,117.8]MPa,10级载荷谱中1~6级为损伤载荷,7~9级为强化载荷,第10级载荷为无效载荷。联立式(6)和式(7),计算强化载荷疲劳强度增比,结果如表7所示。
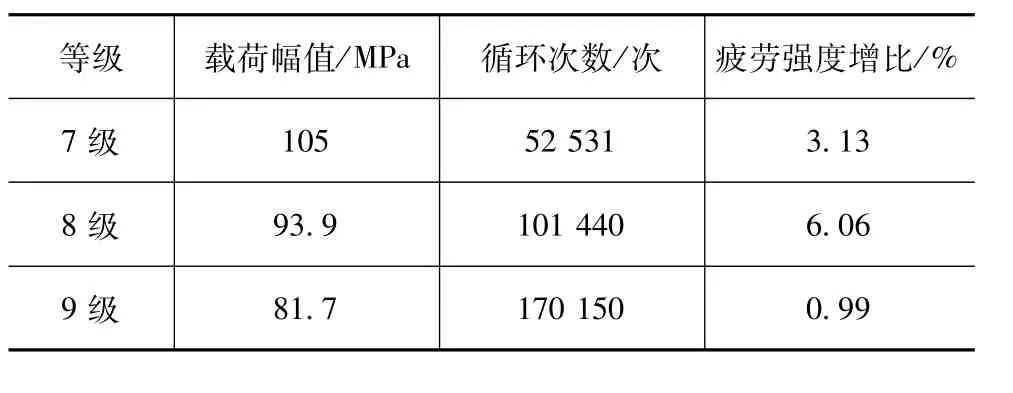
表7 强化效果统计表
对于疲劳寿命的预估,S-N曲线是一个重要的影响因素,对材料S-N曲线的研究发现材料参数m离散性小,材料参数C离散性大[21]。根据低载强化的微观机理可判断强化载荷作用下其S-N曲线的C值随强化载荷作用逐渐提高。若假设转向节原材料S-N曲线为σmN=C0,经低载强化得到修正S-N曲线,材料参数变为C1,该S-N曲线平移至初始S-N曲线上方,如图17所示。曲线显示,低载强化效应表现为在同等应力水平下循环次数的增多或相等循环次数时应力幅值提升,可得关系式为


式中:σ-1,0为原材料疲劳极限,MPa;σ-1,1为低载强化后材料疲劳极限,MPa;N0、N1为相同应力水平下强化前后的疲劳寿命。
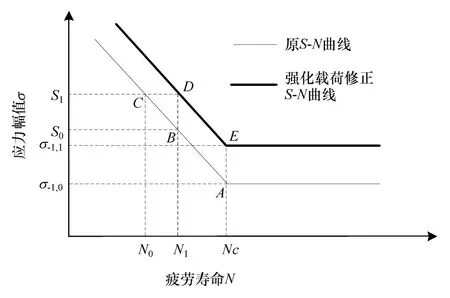
图17 低载强化力学模型
在实际应用中,材料往往经过多级强化载荷,由式(7)和式(8)可求得在某一损伤载荷下的转向节经j个强化载荷作用后的疲劳极限 σ-1,j和疲劳寿命Nj:
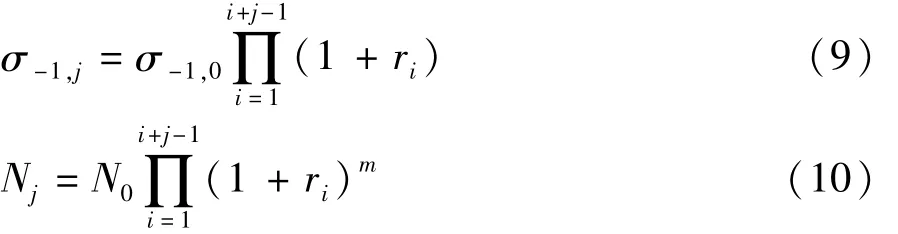
由式(9)可求得在单个加载谱块作用后转向节疲劳极限增比 rL,如式(11)所示,求得 rL=10.4%。
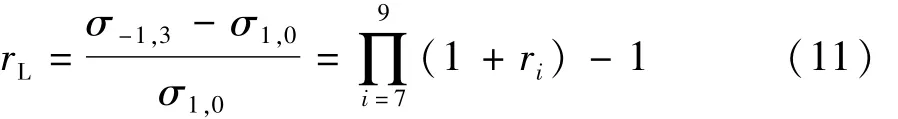
本文中应用名义应力法,即以转向节S-N曲线为基础,结合Miner准则预估转向节疲劳寿命。设转向节S-N曲线的对数表达形式为lgσ=B lg N+A,其中 A=lg C/m;B=-1/m,已知 N=1000时,σ=425 MPa;N=107时,σ=124 MPa,求得 m=7.4,转向节S-N曲线表达式为
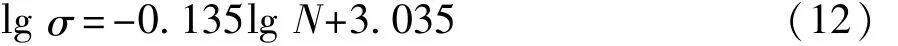
根据Miner准则中损伤定义,10级应力谱中每级损伤载荷造成的损伤量 dj=nj/Nj,nj和 Nj分别为某一损伤载荷下的实测载荷循环次数与疲劳寿命,计算得到每级载荷下的转向节损伤量如表8和表9所示。
结合线性累积损伤理论中总损伤D=Σdj,表8中计算可得不考虑强化载荷影响的一个谱块的总损伤D0=0.1047;表9中考虑强化载荷的影响,材料疲劳极限提高10.4%,计算可得经过单个谱块后疲劳极限 σ-1,3=124×(1+0.104)MPa,即 136.9 MPa,大于第6级载荷幅值。基于Miner准则,不考虑低于疲劳极限应力的损伤作用,求解一个谱块的总损伤 D1=0.07196。
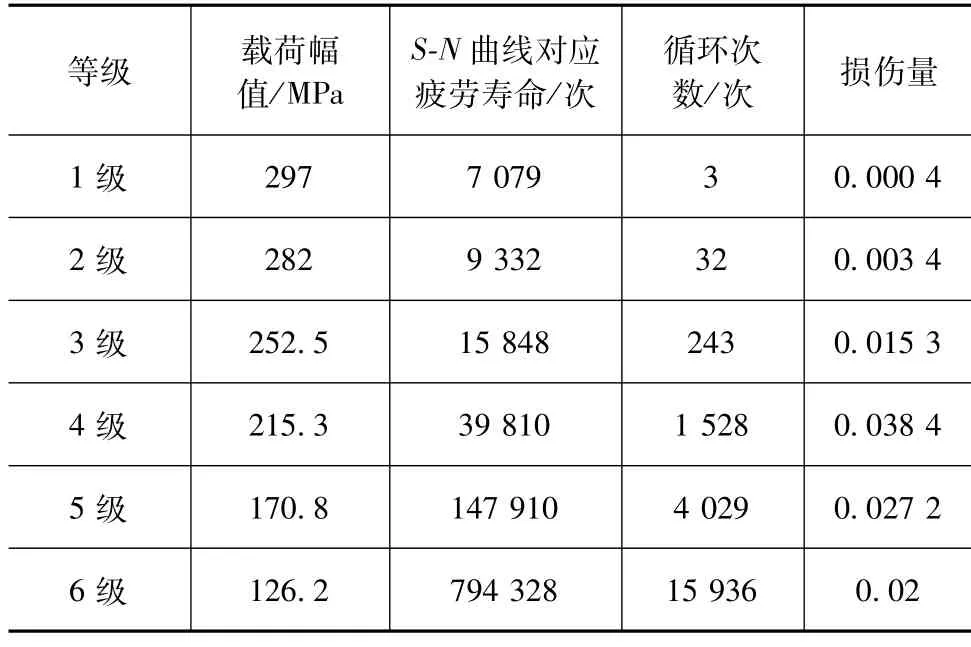
表8 不考虑低载强化影响的转向节损伤量统计表
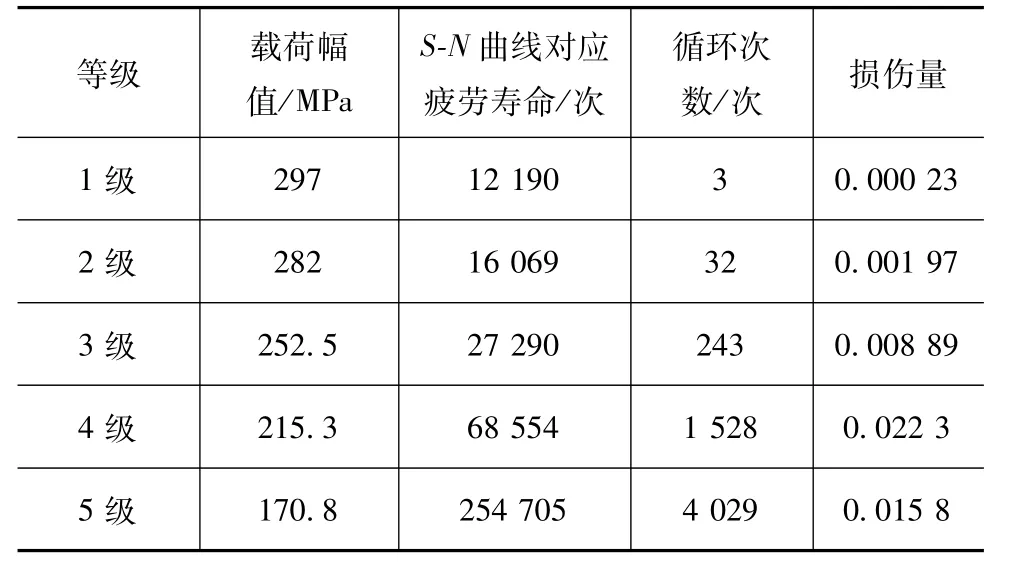
表9 考虑低载强化影响的载荷谱损伤量统计表
当发生疲劳失效时,取构件累计总损伤 D=0.7,已求得考虑小载荷强化效应的谱块损伤量D1=0.07196,计算得疲劳寿命 L1=D/D1=9.7(块);不考虑强化载荷影响的谱块损伤量D0=0.1047,计算得疲劳寿命 L0=D/D0=6.9(块),疲劳寿命提高比为40.6%。
4 结论
(1)利用室内振动台架开展整车多工况激振测试,并以实测轮心六分力为转向节动载损伤仿真激励,获取多工况转向节损伤云图,从而确定转向节疲劳损伤危险点。
(2)基于最小标准差原理,得到能够真实反映试车场路面特征的应变载荷谱,并应用伪损伤保留法进行加速编辑,在穿级计数统计和能量谱密度等方面验证加速谱的有效性。
(3)采用等间隔法将传统8级谱的强化载荷再次分级形成10级谱,充分反映了低载强化效应,并将其转化为对材料S-N曲线参数C的影响,推导求解相同水平应力下低幅载荷强化前后材料疲劳寿命与疲劳强度的提升比例关系,结合初始S-N曲线和Miner准则获取了材料强化前后每级损伤载荷的损伤量,分析表明低载强化效应使转向节疲劳寿命提高 40.6%。

