安装ECAS和液压互联悬架的客车动态性能研究*

綦衡敏，张 农，2，王 东，张邦基，郑敏毅

（1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.合肥工业大学汽车工程技术研究院，合肥 230009；3.合肥工业大学汽车与交通工程学院，合肥 230009）

前言

公路运输是我国主要的运输方式之一，客车是公路运输的主要交通工具。客车因为质心高和载质量大，其悬架设计应着重考虑操纵稳定性和平顺性之间的平衡［1］。空气悬架因其刚度的非线性、较低的垂向频率可显著改善平顺性能而被客车广泛应用［2］。横向稳定杆常用以保证操纵稳定性，然而，选用细一点的稳定杆，可提升平顺性，但侧倾角刚度不足，会造成操纵稳定性下降；选用粗一点的稳定杆，有足够的侧倾角刚度，可保证操纵稳定性，但会降低平顺性能。因此，带横向稳定杆的传统悬架结构难以兼顾只能折中这两种性能。本文中提出的RHIS与ECAS结合的新型悬架系统旨在解决这一问题。

抗侧倾液压互联悬架（roll-resistant hydraulically interconnected suspension，RHIS）技术因能显著改善客车弯道行驶稳定性而首先在赛车和豪华轿车上得到应用［3］。Zhang和Smith等针对RHIS系统开创性地提出了频域和时域建模分析方法，并对所建的系统模型进行了台架验证［4－5］。姚麒麟和甄昊研究了与此类似的可切换式交联悬架系统，并在某越野车上进行了静态建模仿真和测试验证［6－7］。刘旭晖等针对装有RHIS系统的某越野车进行了抗侧倾性能研究［8］。Tan等将一款新型的液压互联悬架系统应用于救护车上，主要改善平顺性以减少二次损伤［9］。华卉等对安装RHIS的客车进行了建模和试验分析［10－11］，但仅局限于操纵稳定性提升方面，未对空气悬架进行细化分析。综合以上文献，针对客车匹配RHIS悬架的研究还较少，其综合性能有待进一步全面评估。

本文中以某客车为研究对象，提出 RHIS与ECAS结合的新型悬架系统，考虑空气弹簧非线性和悬架高度调节控制等因素，仿真对比其在操纵稳定性和平顺性方面相对于原车的优势。

1 客车动力学模型

1.1 空气弹簧建模与验证

本文中样车采用带直筒型附加气室的膜式空气弹簧，如图1所示。主要由主气室、附加气室和节气孔等 3部分组成。其中，pt、pe、Vt、Ve、mt和 me分别表示主气室和附加气室内气体的绝对压力、体积和质量。

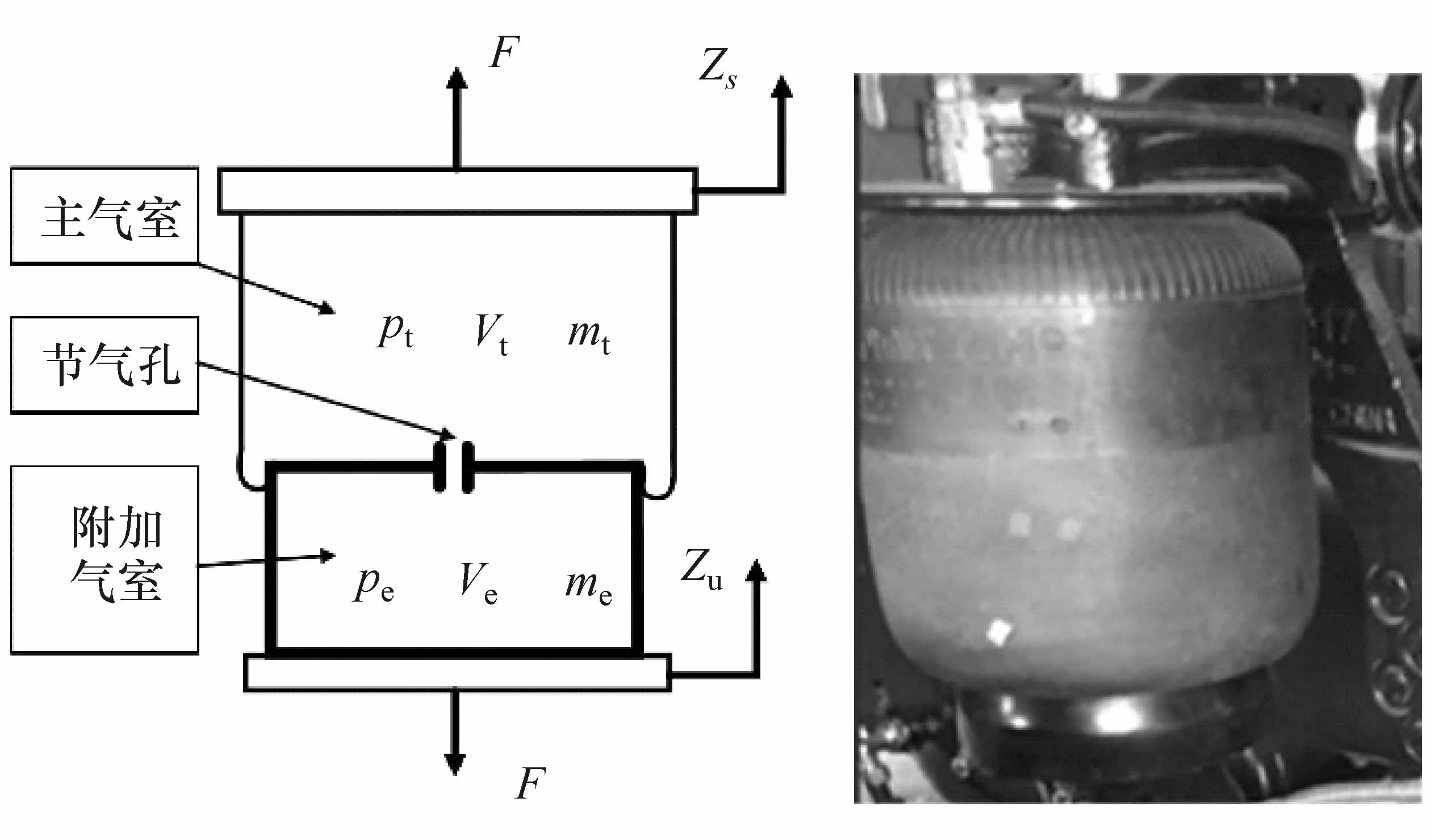
图1 空气弹簧物理模型（左）和实物图（右）

（1）主气室动力学模型

将主气室内的气体视为理想气体，则各状态变量满足理想气体状态方程：

式中：R为空气常数；Tt为主气室内气体温度。对式（1）两边进行微分可得

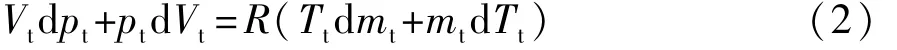
由热力学第一定律可知，开口系统气体能量变化方程为

式中：d Q为橡胶气囊内气体与外界交换的热量；d E为气体内能增量；d W为橡胶气囊内气体所作的膨胀功；Cp为气体定压比热；T′为流入或流出主气室气体温度。一般情况下主气室与附加气室内气体温度之比小于1.1，所以这里认为 T′≈Tt。根据工程热力学，气体内能的增量d E和膨胀功d W为

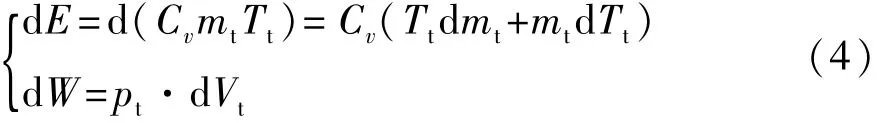
式中Cv为气体定容比热。空气弹簧动态振动过程被认为是绝热过程，主气室气体与外界热量交换很小，d Q≈0。根据迈耶公式，并将气体定压比热Cp和气体定容比热Cv的比值定义为绝热系数k，可得

式中主气室内气体质量变化率可用流入或流出主气室的质量流量Qt表示。

（2）附加气室动力学模型

附加气室也属于开口变质量系统，但由于附加气室的容积固定不变，参考主气室数学模型，则附加气室的数学模型为

（3）节气孔动力学模型

节气孔是为限制主、附气室间的气体交换，其流量特性公式为

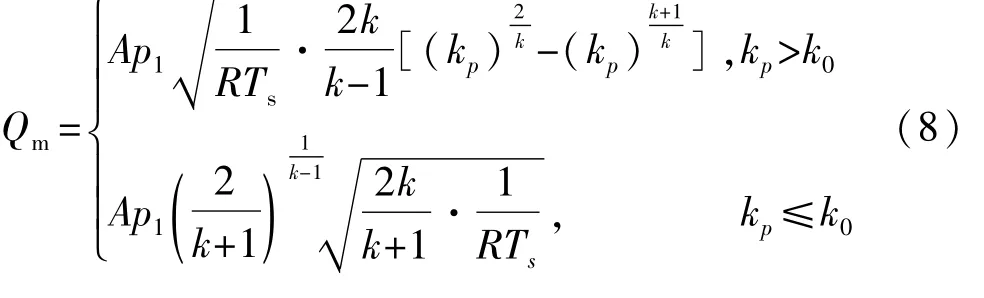
式中：p

1

为节气孔上游端绝对压力，p

1

＝max｛p

t

，p

e

｝；p

2

为节气孔下游端绝对压力，p

2

＝min｛p

t

，p

e

｝；A为节气孔有效流通面积；k

p

为节气孔上下游压力之比（Q

m

可视为 k

p

的函数）；k

0

为临界压力比，k

0

＝0.518，当压力比大于临界压力比时为亚声速流，当反之则为超声速流。

空气弹簧的有效面积通过等温等压静弹性特性试验获得。试验在电液伺服试验机上进行，先将空气弹簧调至标准高度，充入初始气压并保留气源。激振台将空气弹簧压缩至最大压缩状态并停留5 min，再以10 mm／min的速度将气囊拉伸到最大拉伸状态。试验中要求内部压力始终维持初始压力，从最大压缩状态开始，每变形10 mm记录一次负载值。本文中对空气弹簧在0.3、0.5和0.7 MPa 3种初始气压下进行测试，得到等压静特性曲线和有效面积曲线，如图2所示。将空气弹簧有效面积视为空气弹簧高度变化量的函数，可拟合得到空气弹簧的有效面积表达式：

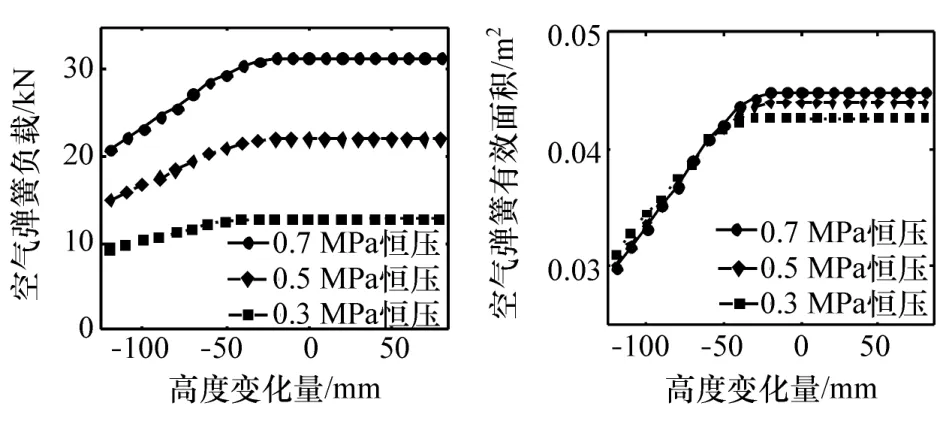
图2 空气弹簧等压静特性（左）和有效面积（右）曲线

针对以上模型，使用空气弹簧的动弹性特性试验进行验证。试验中先将空气弹簧调至标准高度，充入气体至初始气压，然后断开气源，激振台以±70 mm的振幅、0.4 Hz的频率施加垂向正弦激励，试验10个循环，记录最后一个循环的负载 变形曲线。本文中对空气弹簧在0.3、0.5和0.7 MPa 3种初始气压下进行垂向正弦激励。在Simulink中搭建空气弹簧模型并按照相同工况运行得到仿真数据，将仿真数据与试验数据进行对比，如图3所示。由图3可以看出，所建模型与试验结果吻合度非常高，验证了模型的有效性。

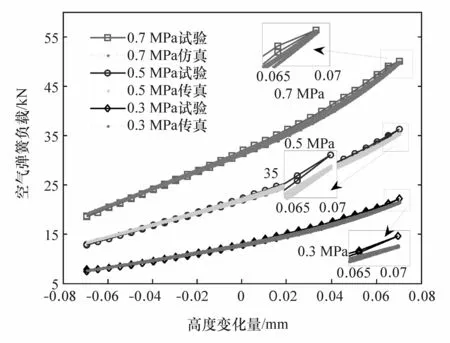
图3 空气悬架动弹性特性验证对比曲线

1.2 整车模型的建立

为了研究整车的操纵稳定性和平顺性，本文中针对目标客车，在带附加气室空气弹簧非线性模型的基础上，建立了整车9自由度模型，如图4所示。在不考虑结构振动［12－13］和车身柔性［14］的假设下，9自由度包括车身垂向、侧倾、俯仰运动，整车的侧向和横摆运动，以及与车轮对应的4个簧下质量的垂向运动。Zs表示簧载质量质心处垂向位移；φ表示车身侧倾角；θ表示车身俯仰角；ψ、Zy分别表示整车横摆角、横向位移，Zui（i＝1，2，3，4）分别表示 4个簧下质量的垂向位移，Zgi（i＝1，2，3，4）分别表示 4轮受到路面的激励。客车模型中整车主要参数［15］见表1。

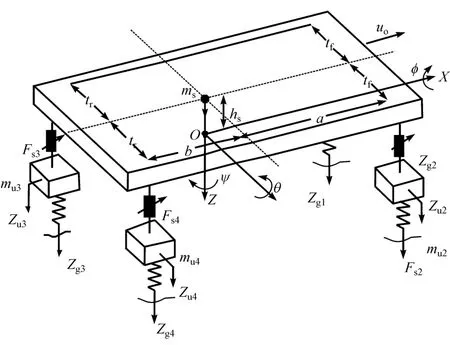
图4 整车9自由度模型

根据质心定理和动量矩定理推导出整车动力学方程，此处限于篇幅，仅给出最终结果。

整车侧向平动方程为

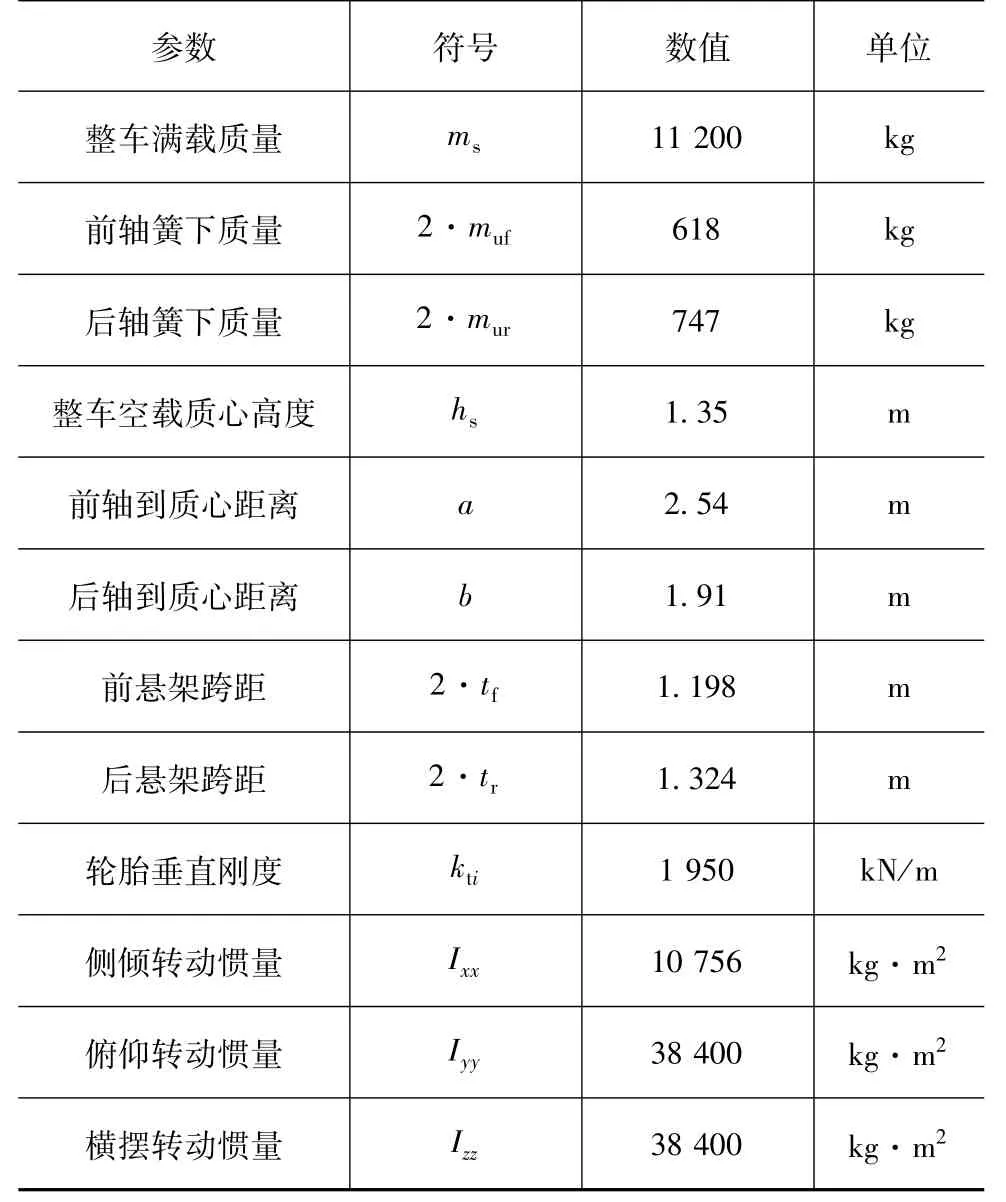
表1 整车参数

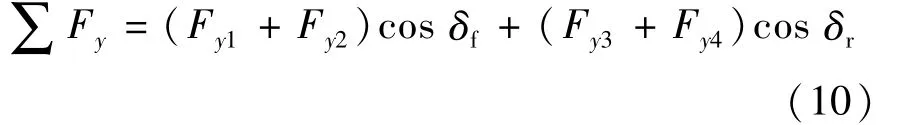
式中：δf和 δr分别为前、后轮的转向角；Fyi（i＝1，2，3，4）为4个车轮的侧向力。采用“魔术公式”计算轮胎的侧向力和回正力矩等动态力：

F＝D sin｛C arctan［Bx－E（Bx－arctan Bx）］｝ （11）

式中：F为轮胎所受的动态力和力矩；x为轮胎侧偏角或滑移率等参数；D为峰值因子；B为刚度因子；C为曲线形状因子；E为曲线曲率因子。针对不同的动态力和力矩，有对应的一套参数用于计算。

样车使用315／80R22.5轮胎，参考 Adams中相同型号轮胎参数，可得侧向力特性，如图5所示。

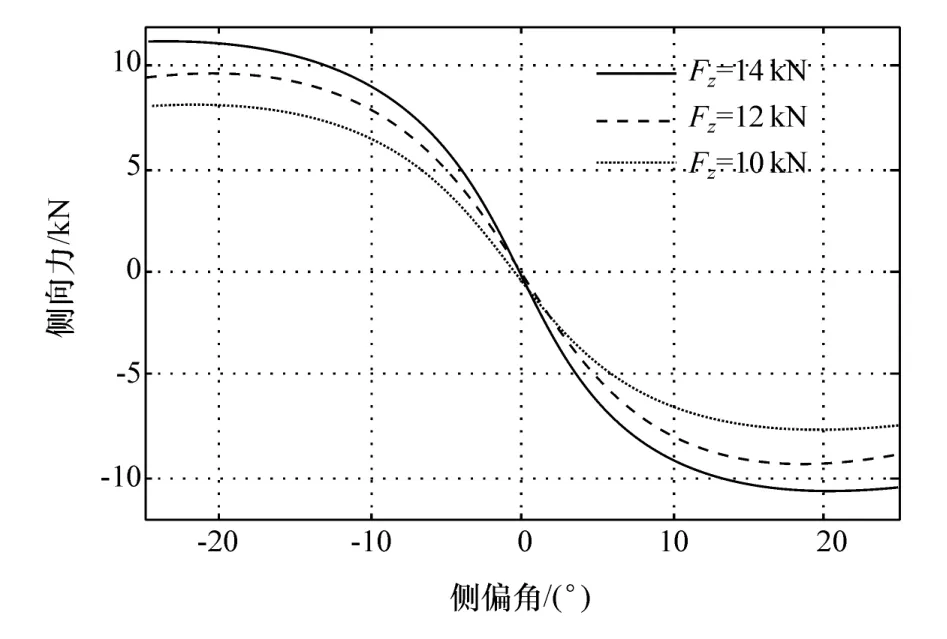
图5 型号315／80R22.5轮胎侧向力特性曲线

簧上质量垂向运动方程为

式中Zsu1、Zsu2、Zsu3和Zsu4分别为4个悬架的动行程，根据运动学关系，可表示为

横摆、侧倾和俯仰动力学方程分别为

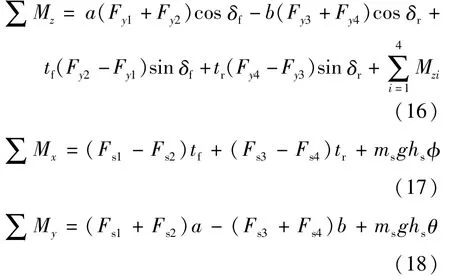
式中 Mzi（i＝1，2，3，4）为地面作用于轮胎的回正力矩，可由前述的轮胎“魔术公式”计算获取。

综上，整车9自由度模型矩阵微分方程可写成：

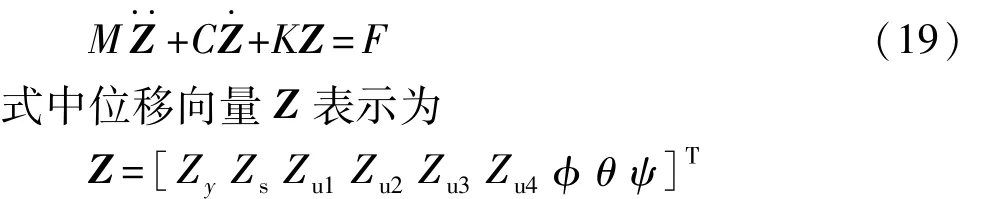
1.3 整车耦合模型与试验验证

（1）RHIS原理

RHIS系统构成如图6所示。系统通过安装在悬架位置的4个作动器交叉互联而构成两条液压回路，每个回路中含有一只蓄能器和若干阻尼阀。图中，Qi、pi和Ai分别为各位置上的液压流量、压力和截面积。

对于车身的垂向和俯仰运动，前后悬架垂向跳动时，同轴左右作动器同向运动，同一回路油液可左右交换而很少进入蓄能器，两回路压力变化小，几乎不增加垂向和俯仰刚度，从而对车身的垂向和俯仰模态影响很小。但当车身侧倾时，同轴左右作动器反向运动，悬架位移导致两回路油液较大流量进出各自蓄能器而使两回路产生较大压差，在压差的作用下4个作动器综合对车身产生抵抗侧倾的力矩，将车身拉回到平衡状态，从而减小弯道行驶的侧倾趋势，故对车身的侧倾模态起到很好的控制作用。

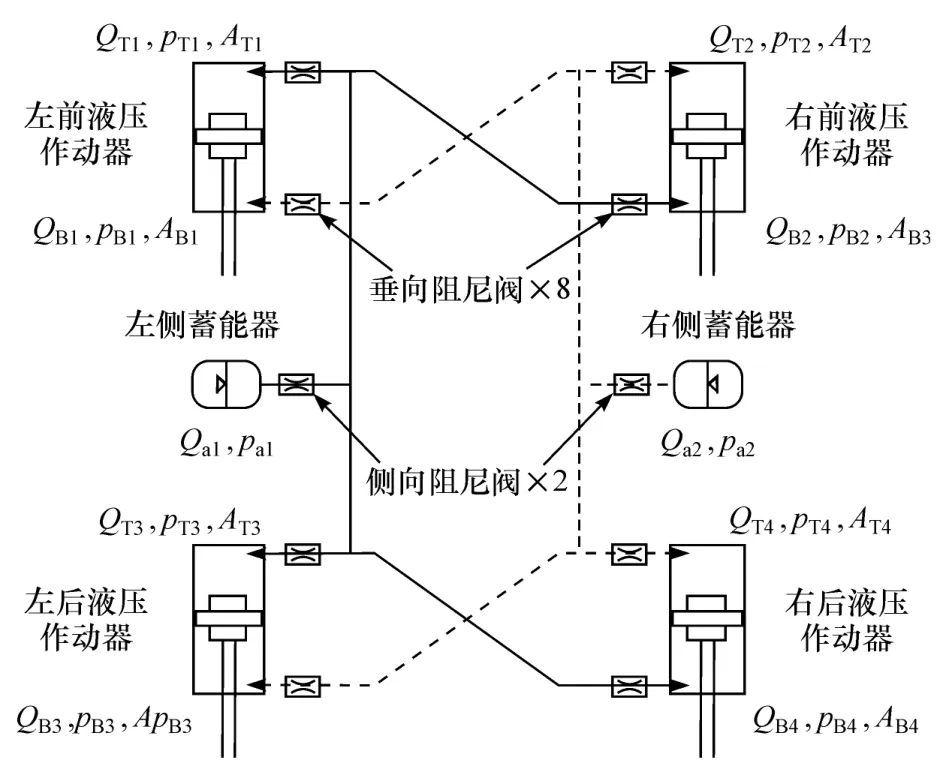
图6 RHIS系统原理图

回路中的垂向阻尼阀等效原车减振器，衰减垂向振动，而侧倾阻尼阀可衰减侧倾振动，以改善乘坐舒适性。综上，RHIS系统可实现对车身垂向、俯仰和侧倾模态的刚度和阻尼解耦，提供非线性的侧倾刚度和阻尼，可在大幅提升操纵稳定性的前提下保证乘坐舒适性。

（2）整车耦合模型

本文中采用的RHIS系统时域建模方法在文献［5］中已有详述，此处不再赘述。整车耦合RHIS后，状态方程为

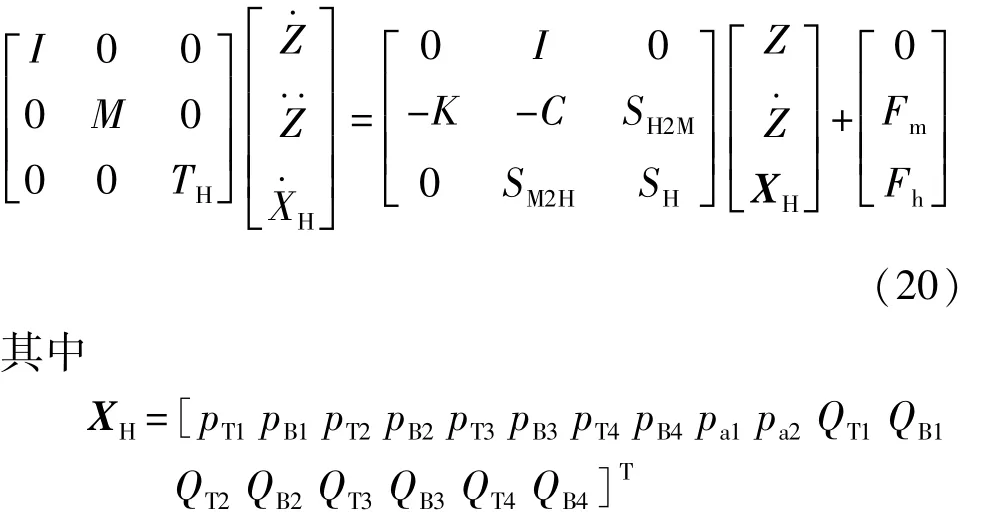
对于原车中安装横向稳定杆的状态，只须在式（20）的基础上在刚度矩阵中加上稳定杆的刚度，即K＝Ks＋Karb。横向稳定杆的刚度矩阵见式（21），式中：kaf和kar分别为前后横向稳定杆扭转角刚度；lf和lr分别为前后横向稳定杆安装长度。

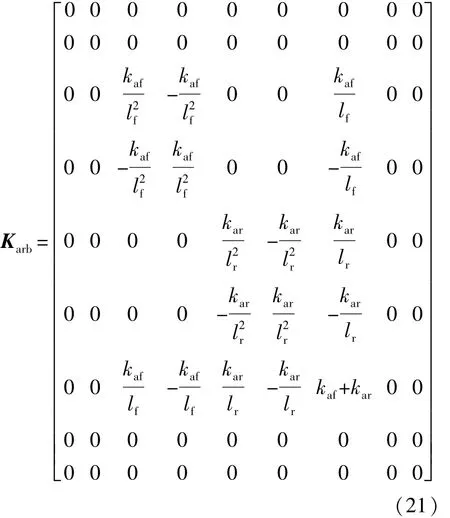
（3）模型验证

针对以上模型，参考国标［16］在东风汽车试验场开展实车测试对模型进行验证。试验现场的整体布置如图7所示，图中间位置为可装两种悬架状态的样车，图右侧为安装在车身上的GPS和惯性测量单元（IMU），主要用来测量运行中的车速和车身姿态，左下角的转向机器人主要测量转向输入，试验由专业驾驶员进行操作，以上所有传感器测量的数据都通过左上角的数据采集系统获取，并由试验工程师实时审查和保存，确保数据的有效性。对比原车状态和安装RHIS状态的侧向加速度、侧倾角和横摆角速度试验数据和仿真数据，分别如图8和图9所示。蛇行工况车速定为75 km／h。从图中可以看出，两种客车状态下的仿真数据与试验数据吻合较好，验证了所建仿真模型的正确性。

图7 实车测试布置图

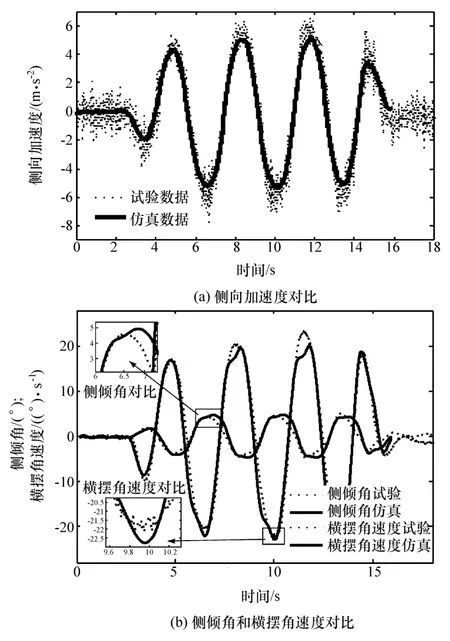
图8 原车状态模型验证

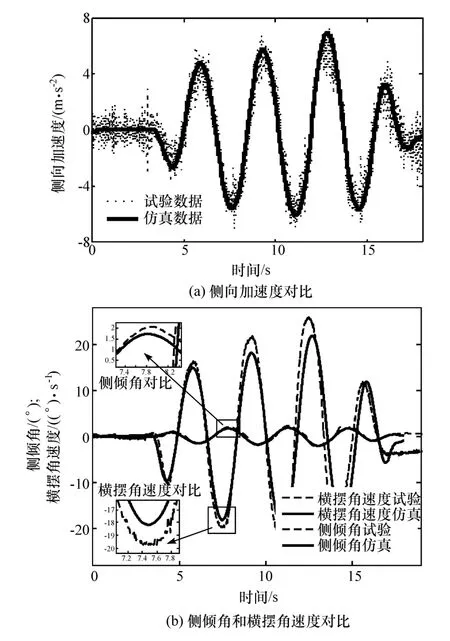
图9 安装RHIS状态模型验证

2 ECAS高度调节控制策略

2.1 车身高度模糊控制设计

本文中采用二维模糊控制器结构，选取4个悬架动行程与目标抬升高度的偏差及其变化率作为输入，给电磁阀的开关信号作为控制系统的输出，向各个空气弹簧充放气，达到调节车身高度的目的。文中选用梯形和三角形隶属函数设计双输入单输出的模糊控制器，规则见表2，其输入输出变量模糊规则的三维图如图10所示。

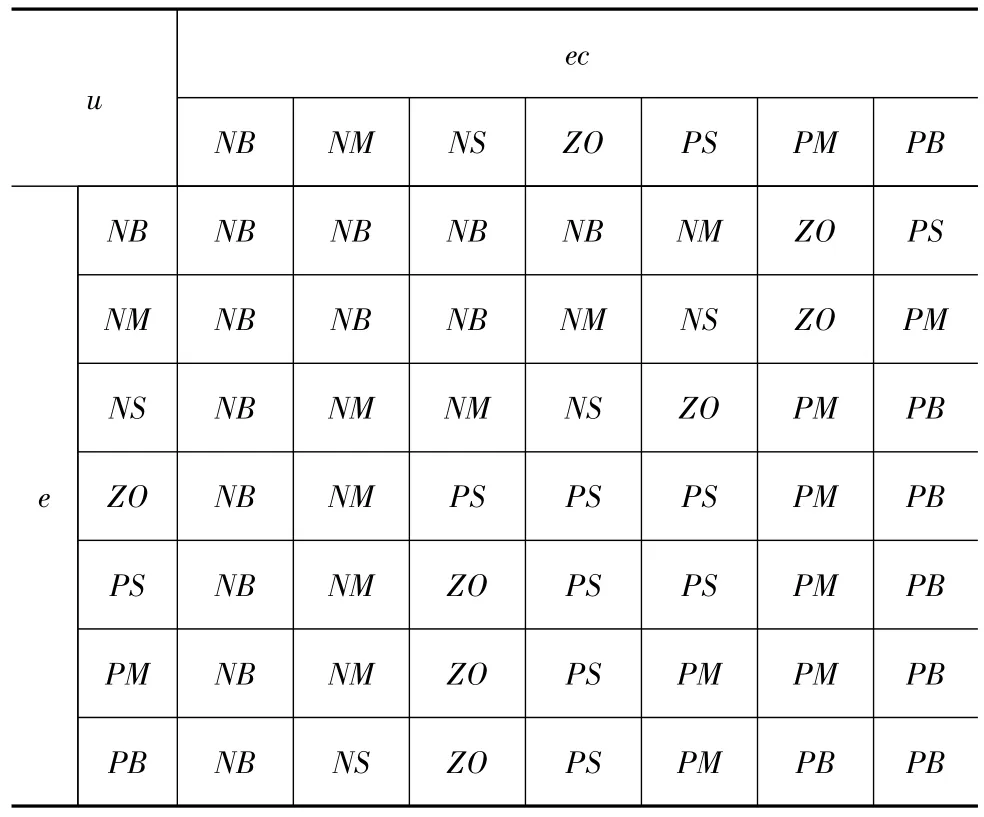
表2 模糊控制规则表

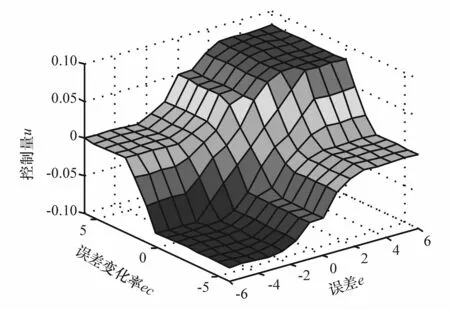
图10 模糊控制规则三维图

在Simulink环境中搭建模糊控制器，空气弹簧的高速电磁阀采用PWM波控制开关。将上述控制模型耦合在安装了空气弹簧和RHIS的整车9自由度模型中，搭建成一个完整的可通过充放气进行客车车身高度调节的模型，如图11所示。

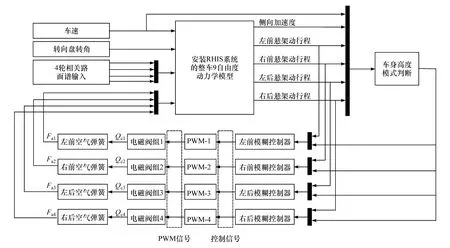
图11 整车9自由度车身高度调节模型

2.2 仿真分析

使用图11的模型对客车处于静止和随机路面激励时进行高度调节。图12为两种状态下车身高度调节的仿真结果，选取了左前和右后悬架作为参考。静态时，系统在2 s左右初次达到目标高度，随后有5 mm以内的超调量，约4 s后，系统在目标高度位置保持稳定，且具有较好的控制精度。动态时，仿真在A级路面上进行，客车可在2 s内首次调整到目标车身高度值，且在3 s内基本维持稳定，满足对高度调节功能的要求。由于客车所受外界干扰不太强烈，控制器基本可以稳定在目标高度上下，误差最大值在［－0.01，0.01］m的范围内。

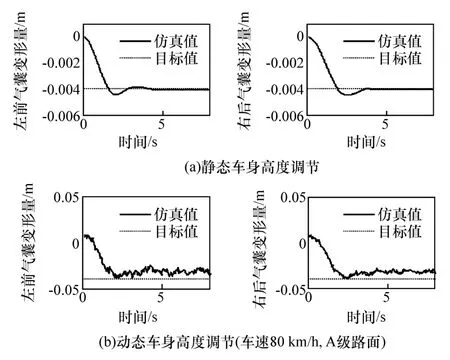
图12 动静态车身高度调节仿真结果

3 整车性能仿真分析

3.1 操纵稳定性

为了研究安装新型悬架客车的操纵稳定性，本文中针对4种不同状态的客车进行操稳性仿真，客车各悬架形式和车身高度模式见表3，表中RHIS系统参数选择如下：蓄能器预充气压为1.4 MPa，容积为1.0 L；前后液压作动器上腔面积 AT1＝AT2＝AT3＝AT4＝3.85×10－3m2，下腔面积 AB1＝AB2＝AB3＝AB4＝3.23×10－3m2；前后轴作动器安装跨距，前跨距为0.94 m，后跨距为 1.12 m；系统稳态压力设定为2.3 MPa。表中前后横向稳定杆参数选择如下：kaf＝3079 N·m／（°），kar＝3505 N·m／（°）。仿真工况选用60 km／h的蛇行绕桩试验，整理得到侧倾角和侧翻临界因子（RCF［17］）数据，分别如图 13和图 14所示。

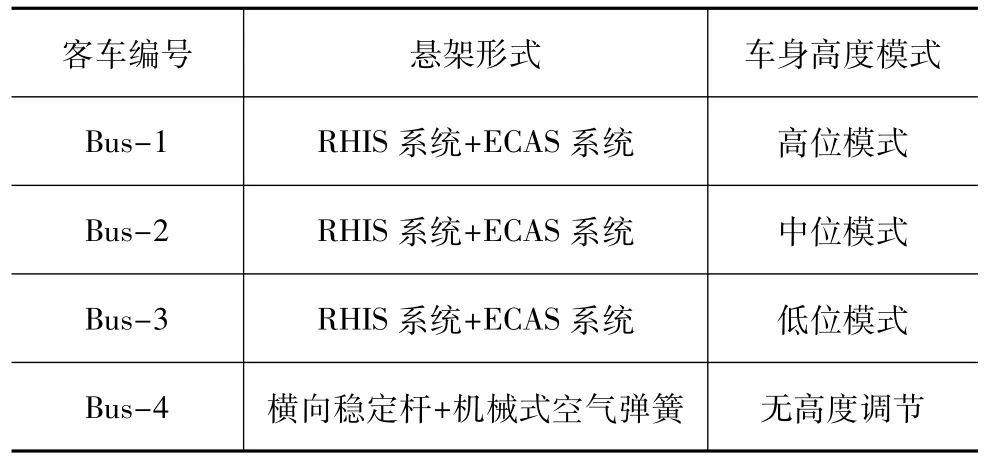
表3 操纵稳定性试验中客车悬架类型

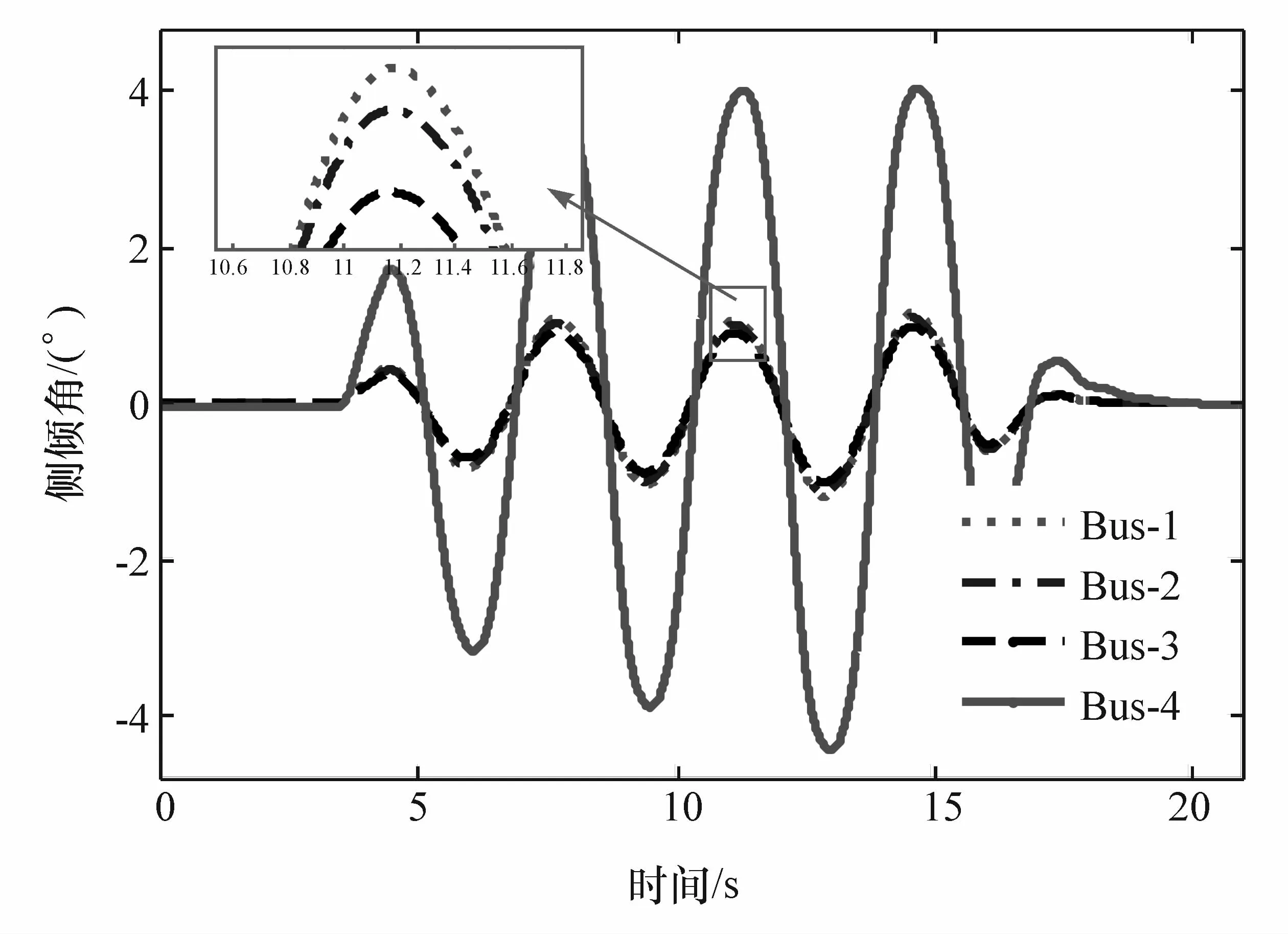
图13 蛇行试验侧倾角仿真结果

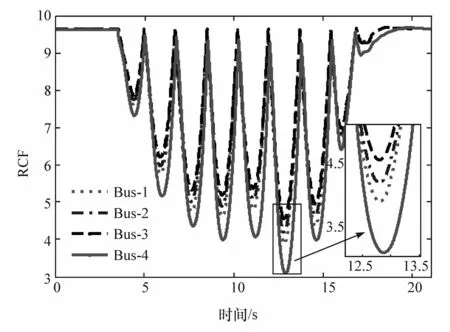
图14 蛇行试验RCF仿真结果

由图13可见，安装传统悬架系统的客车，仿真中侧倾角的最大值为4.1°，而安装新型悬架系统的客车的最大侧倾角显著减小，高、中、低3种高度模式的侧倾角最大值分别为 1.44°、1.35°、1.21°，低位模式相比高位模式侧倾角约减小了16%，比传统悬架减小了70.5%。可知，安装新型悬架系统可明显提高客车的抗侧倾能力，且当客车高速行驶时，客车切换到低位模式可进一步提高客车的操纵稳定性。

用于评价客车抗侧翻能力的RCF，其数值越大表示越不容易侧翻，当数值为负时表示已经侧翻。从图14可以看出，虽然4种类型客车的RCF值都大于0，表示都未发生侧翻，但安装新型悬架系统的客车RCF显著大于安装横向稳定杆的传统客车，这表示安装新型悬架系统的客车抗侧翻能力显著改善。同时，客车处于低位模式时，RCF值更大表示客车质心低更不容易发生侧翻，可提高客车的安全性。

3.2 平顺性

为研究安装新型悬架系统对客车平顺性的影响，参考国标［18］开展60 km／h速度下的C级路面随机输入试验和50 km／h速度下脉冲输入仿真试验，对比传统悬架系统的客车和处于中位高度模式的新型悬架系统客车的簧上质量垂向加速度，仿真结果如图15和图16所示。

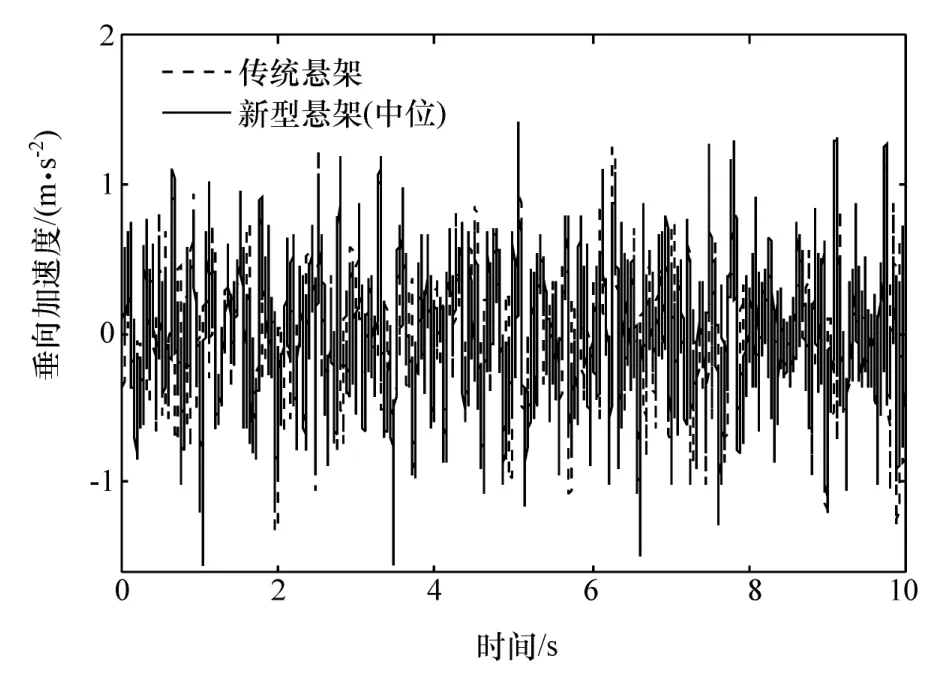
图15 传统和新型悬架客车随机输入下响应对比

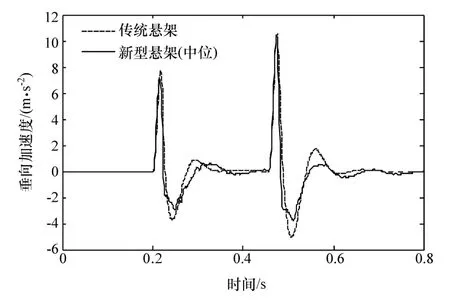
图16 传统和新型悬架客车脉冲输入下响应对比

由图15可见，安装传统悬架和处于中位高度模式的新型悬架系统客车的垂向加速度均方根值aw分别为0.466和 0.454 m／s2，垂向加速度峰值 asmax分别为 1.79和 1.74 m／s2，差别不大，但安装了RHIS系统的客车平顺性略好于安装横向稳定杆的客车。由图16可见，脉冲输入仿真中，两者的加速度峰值分别为10.85和10.76 m／s2，相差不大，但在反向峰值处可见新型悬架还是优于传统悬架。综上仿真结果，安装新型悬架系统的客车可在一定程度上改善客车平顺性。

为全面评价新型悬架在3种车身高度下的平顺性，采用同样的工况进行仿真，结果如表4所示。从表4中可以看出，在随机和脉动两种输入激励下，3种高度模式的簧载质心垂向加速度均方根值aw和峰值asmax都相差不大，相对而言高位模式稍好一些。总的来说，不同高度模式下平顺性能基本接近，与原车的平顺性差别不大。

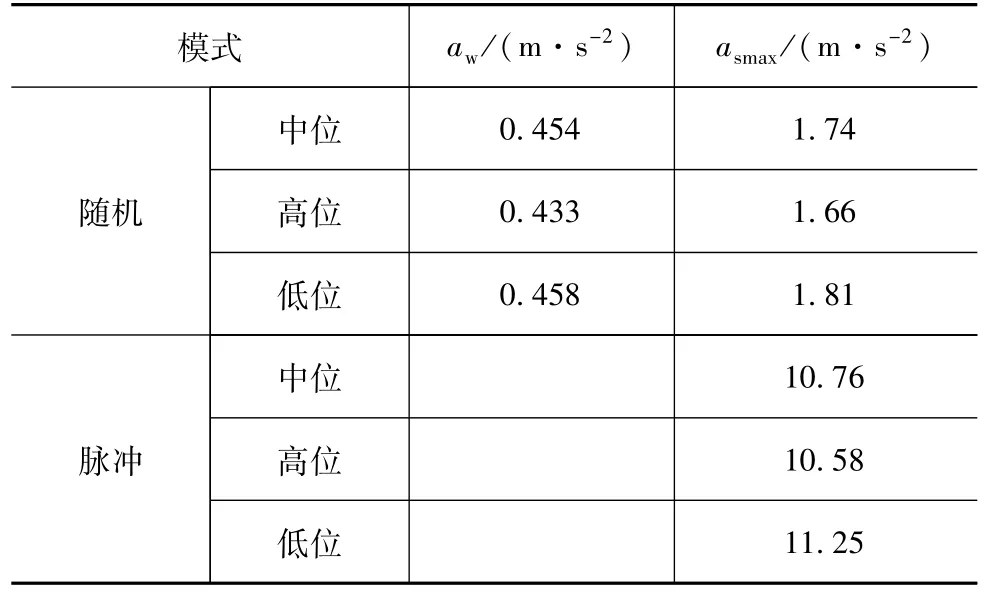
表4 不同高度模式下簧上质心垂向加速度统计结果

4 结论

本文中针对大型客车传统悬架难以兼顾操纵稳定性和平顺性的问题，提出了ECAS与RHIS相结合的新型悬架系统。建立了考虑空气弹簧非线性的整车9自由度模型，通过试验验证了机械 液压耦合动力学模型的正确性。设计了ECAS模糊控制器和车身高度调节控制策略，通过车载传感器的信号可实现车身高度3级可调，具有较好的控制精度。参考国标资料仿真对比研究了新型悬架和传统悬架的操纵稳定性和平顺性。结果表明新型悬架系统可显著改善整车操纵稳定性，高速行驶下降低车身高度能进一步提高操纵稳定性和安全性；与此同时，车辆的平顺性也稍有改善。