基于灵敏度分析-中心组合设计的乘用车发动机舱温度场优化

王其东，张 杰，张 民

（1.安徽理工大学机械工程学院，淮南 232000； 2.奇瑞商用车（安徽）有限公司工程研究院，芜湖 241000）

前言

随着人们对乘用车安全性、动力性和经济性的要求不断提高，以及国家对排放标准的严格控制，乘用车的发动机舱布置越来越紧凑，发动机的强化程度越来越高且热负荷增大［1－2］，极易导致发动机舱零部件温度超标，严重影响车辆安全和部件使用寿命。

为解决该问题，国内外学者做了很多有意义的研究。计算流体力学仿真技术被广泛应用于发动机舱的流场和温度场分析中［3－5］，通过仿真可获得发动机舱内流场和温度场的分布，在设计前期为发动机舱布置设计提供指导，有效避免了产品后期大的改动，降低了工程成本［6－8］。刘桂兰等人分析了不同进气面积和换热器与发动机的间距对舱内温度场的影响［9］。刘念等人采用CFD仿真技术对发动机舱流场和发动机冷却性能开展耦合研究，提出优化变量改进后的离散值并通过正交试验找出了满足性能要求的优化组合［10］。刘水长等人提出了双场耦合强化散热原理，并将空气速度和温度梯度的0°夹角原则应用于发动机舱温度场问题的改进过程中［11］。Khaled等人提出了通过简化模型和优化空间布置解决发动机舱温度场问题［12］。Ou等人根据热传递理论和场协同原理解决了汽车发动机舱的传热问题［13］。

分析文献发现，目前的研究主要是通过CFD仿真分析，从布置、传热和流场等角度找出温度场的影响因素，依据仿真结果和经验给出影响因素的水平值，并通过对各影响因素水平值的组合来确定最终的优化方案。这些研究在一定程度上解决了发动机舱温升问题，但如何系统而全面地找出主要影响因素并确定各因素水平在一定范围内的最优值，需要进一步研究。

本文中提出一种“仿真分析-灵敏度分析-中心组合设计-仿真与试验验证”的分析方法。以某搭载缸内直喷涡轮增压发动机的整车热管理试验开发过程中遇到的传动轴护套表面温度超标问题为例（工况：速度60 km／h，坡度9%，满载，环境温度38℃，环境湿度50RH%；温度场试验值143℃，温度限值120℃），首先，对发动机舱温度场进行仿真分析，找出问题部件温度超标的影响因素；其次，通过灵敏度分析找出主要影响因素；然后，采用中心组合设计方法和二次多项式回归方程，建立问题部件表面温度预测模型，进而确定主要影响因素参数的取值。试验结果表明，该方法能有效降低问题部件表面温度并满足温度限值。

1 模型建立与仿真分析

1.1 理论基础与仿真模型的建立

因发动机舱内空气流动速度远小于声速，故在计算中把空气视为不可压缩理想气体，可近似为常数项［14］。发动机舱内流动情况十分复杂，涉及汽车内外流场耦合的过程，整个流场可设为三维定常无压缩湍流运动，湍流运动采用工业上应用较为广泛的Realizable k-ε模型求解，且湍流运动中遵守以下流动和传热的基本方程［15－17］。

质量守恒方程：

式中：ρ为空气密度，取值为 1.101 17 kg／m3；u为空气速度矢量。式（1）为稳态不可压缩流体的质量守恒方程。

动量守恒方程：

式中：p为空气压力；ui和 uj（i，j＝x，y，z）为速度矢量u在x，y，z方向上的分量；Si为3个方向上动量守恒方程的广义源项。

能量守恒方程：

式中：T为空气温度；Cp为比热容；K为流体传热系数；τij为黏性应力；R为通过辐射散热量；ST为黏性耗散项。

本文中分析所用到的Realizable k-ε模型为典型的两方程模型［18］。

湍动能k方程：

式中：k为湍流动能；ε为耗散率；σk和σε为k和ε的湍流普朗特数；Gk为平均速度梯度产生的湍动能；μ为分子黏性系数；μt为湍流黏度系数；v为合成气流相对速度。

Realizable k-ε模型是针对充分发展的湍流建立的，汽车零部件表面气流流动由于受湍动黏度的影响，零部件附近局部区域雷诺数较低，湍流未充分发展起来［19］。针对Realizable k-ε模型这一局限性，本文中采用壁面函数法进行特殊处理，在不需要对壁面区气体流动求解的前提下即可得到壁面相邻体积的节点变量值，为模拟近壁面气体的流动提供高效、合理和精确的计算。

在尽量不影响流场分析结果的前提下，对底盘和外饰部件进行适当简化，发动机舱主要部件全部保留，在重点热源、进气格栅和温度超标问题点附近区域进行网格加密处理。计算模型采用面网格和四面体网格搭建，整车总体网格尺寸取8～20 mm，加密网格尺寸取3～5 mm，发动机舱网格模型见图1。综合考虑硬件计算能力和计算精度，本文中取模拟风洞的流体域为长方体计算域：车前空间为2倍车长，车后空间为5倍车长，总高为3.5倍车高，车身两侧空间均为2.5倍车宽。精确定位试验测点位置，确保仿真时部件温度值取点与试验测点对应。

图1 发动机舱网格模型

风扇采用MRF模型，建立独立的风扇旋转区域［20］。前端换热部件由低温散热器 冷凝器-高温散热器-冷却风扇组成，通过零部件单体试验获得其阻力曲线，如图2所示。风扇转速采用试验时实际转速1 800 r／min，详细仿真分析工况见表1。

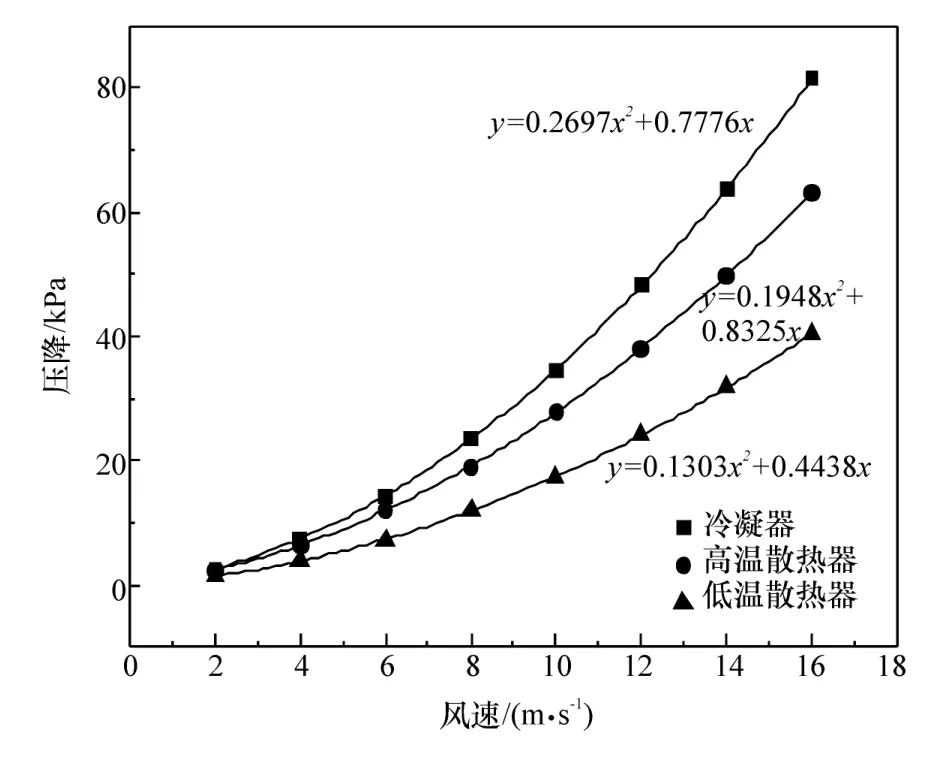
图2 换热部件阻力曲线

表1 工况环境

1.2 仿真结果与分析

在设定内外流场计算域分析模型后，采用STAR－CCM＋软件对其进行仿真计算。得到传动轴护套表面温度为147.7℃（见图3），与试验值143℃相吻合，说明仿真模型的建立和边界条件的设定是合理的。进一步分析发动机舱流场可知，流入舱内的冷却气流从两个方向流出舱外：一个流向为换热部件-发动机上部-三元催化器-副车架上部-发动机舱尾部流出；另一个流向为换热部件-发动机下部-副车架上部流出。发动机舱两个不同截面的空气流速云图见图4和图5。由于传动轴护套距离高温热源（三元催化器）很近，其表面因辐射换热获得大量热量，发动机舱流经传动轴护套表面气流流速较小（约1 m／s），气流很难有效带走其表面热量，导致传动轴护套温度超标。

由图5可见，换热部件左右两侧与安装框架之间存在较大间隙，导致气流从两侧泄漏，从而流入发动机舱内的冷却气流减少，间接导致传动轴护套附近散热困难。

图3 传动轴护套表面温度云图

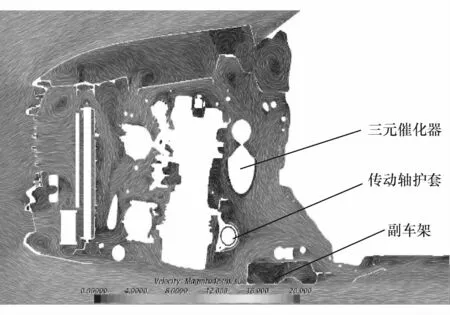
图4 Y＝0截面空气流速云图

图5 Z＝382 mm截面处空气速度云图

2 基于灵敏度分析的温度场关键因素确定

传动轴护套距离三元催化器距离较近，虽然热管理开发试验过程中已通过增加传动轴隔热罩进行隔热，但由于护套附近冷却气流流速低、散热困难，仅通过隔热很难彻底解决热量聚集的问题，必须有效改善护套附近空气流动状态，以降低护套表面温度。结合发动机舱实际布置环境最终确定以下因素，并进行重点分析。

（1）散热器开口比α。α定义为：设去除被遮挡面积后，前格栅正投影到散热器芯体的面积为S1，散热器芯体面积为S2，则

通过对α的调整（当前α为22.3%）提升发动机舱冷却空气进气量。

（2）导流板姿态参数L和θ。导流板位于护套前部、发动机下部，见图6（a）所示 Y平面剖视图。通过调整L和θ将流入发动机下部的气流最大限度地导向护套，提升护套周边空气流量，将热量带走。

（3）导流罩姿态参数β。导流罩位于发动机上部，见图6（a）所示Y平面剖视图。通过调整β将流经发动机上部的气流导向护套方向，将热量带走。

（4）换热部件与安装框架之间的封堵区域百分比S。对换热部件与安装框架之间的间隙自下而上进行封堵，以提升发动机舱进气量，S定义为实际封堵区域面积与图6（b）所示3个可封堵区域总面积的比值。

（5）冷却风扇转速 r。适当提高 r（当前状态1 800 r／min），以增加发动机舱进气量。

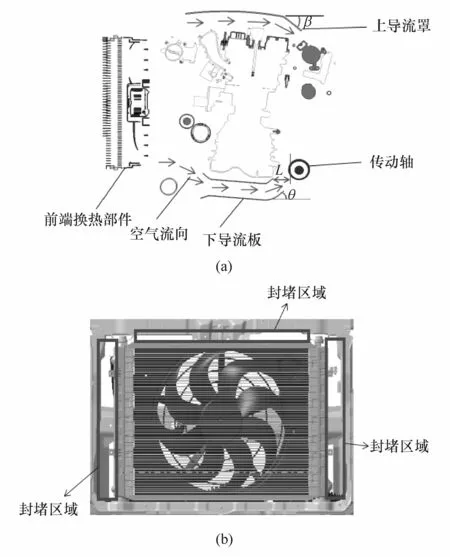
图6 关键因素示意图

为降低传动轴护套表面温度，须综合考虑α、L、θ、β、S和r对周边空气流动状态的影响。为提高分析效率，降低非关键因素对分析结果的干扰，本文中采用灵敏度分析找出影响传动轴护套周边空气流动状态的关键因素。

有限差分法是一种用于计算灵敏度的较常用的分析方法，该方法通过变量摄动的方式计算灵敏度系数，其对函数形式无特殊要求，操作简单，在工程优化实践中得到了较为广泛的应用。其中中心差分法是有限差分法中常用的计算方法，具有计算误差小、精度高等优点。本文中采用中心差分法计算各参数的灵敏度系数，进而依据灵敏度系数筛选影响传动轴护套周边空气流动状态的关键因素。对于一个以x为自变量的函数f（x），灵敏度系数的中心差分法计算公式［21］为

本文中研究的参数为 α、L、θ、β、S和 r。结合整车造型、发动机舱和传动轴护套周边实际边界状态，确定各参数的取值范围，见表2。为对比优化前后各因素对传动轴护套周边空气流速的影响，采用控制变量法对单个参数的灵敏度进行分析。

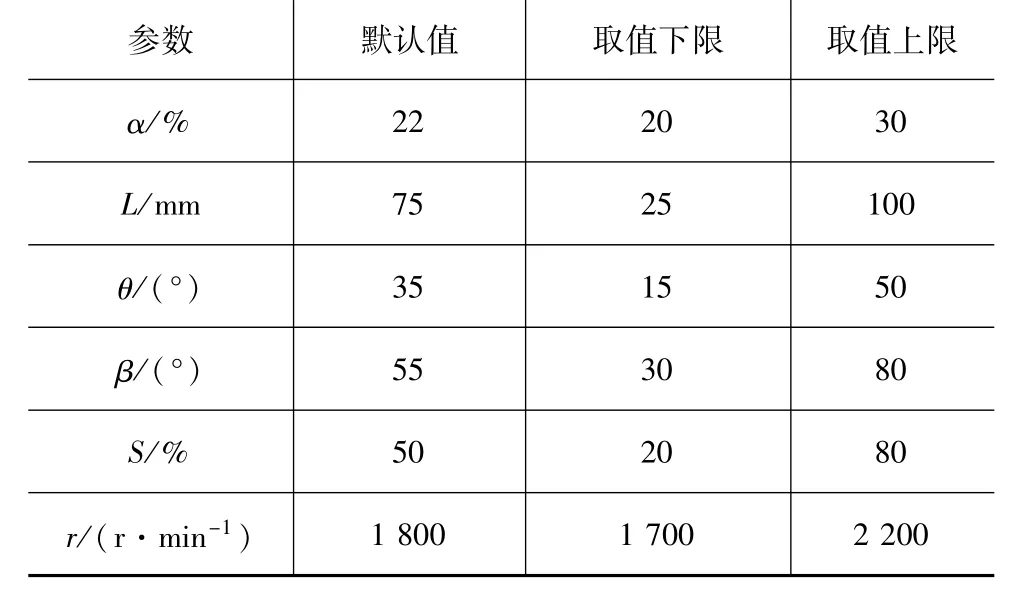
表2 参数取值范围

由表2可知，各参数的数值差别较大，为便于比较，对各参数进行无量纲处理，将各参数与其默认值的比值作为无量纲值，用以计算灵敏度系数。针对每个参数在限制范围内进行流场仿真计算，计算得到的传动轴周边空气流速随各参数的变化规律见图7。采用中心差分法计算护套处风速对各几何参数的灵敏度系数，见图8。各参数改变之后都须对相应方案进行网格划分和边界设定，这对计算结果带来了不同的数值误差，导致灵敏度曲线产生波动，但本文中研究重点是确定不同几何参数灵敏度系数的相对大小进而确定关键参数，并不是获取灵敏度系数的精确值，因此灵敏度曲线的波动对其相对大小产生的影响可忽略。

图7和图8表明，护套处空气流速v随α的增大呈单调上升趋势，灵敏度变化范围为0.4～0.8，绝对值平均值0.73；v随L的增大表现为单调下降趋势，灵敏度变化范围－3.6～－0.4，绝对值平均值2.61；v随 θ的增大呈先上升后下降趋势，在 θ＝1.3处达极大值，灵敏度变化范围－0.9～3.3，绝对值平均值2.03；v随β的增大呈单调上升趋势，灵敏度变化范围0～0.6，绝对值平均值0.35；v随S的增大呈单调上升趋势，灵敏度变化范围1～3，绝对值平均值1.93；v随r的增大呈单调上升趋势，灵敏度变化范围 0.5～1.2，绝对值平均值 0.83。

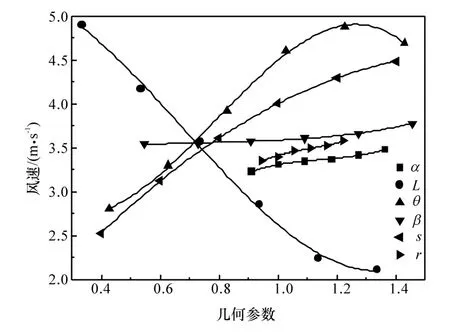
图7 护套处风速随几何参数的变化曲线

图8 护套处风速对几何参数的灵敏度系数

上述计算结果表明，各参数的灵敏度系数由高到低的顺序为 L、θ、S、r、α和 β，其中 S和 r灵敏度系数相差约2倍，由此说明r、α和β为影响传动轴护套周边风速的钝感参数，L、θ和S为影响传动轴护套周边风速的敏感参数。护套表面温度的降低取决于传动轴护套周边风速，因此，要找到降低护套表面温度的最佳方案，必须建立起护套表面温度T与L、θ和S 3个连续变量之间的对应关系。本文中采用中心组合法设计确定最佳降温方案。

3 中心组合设计与温度场优化

3.1 中心组合试验设计

依据传动轴护套周边实际边界条件，距离L取值范围为25～100 mm，夹角 θ取值范围为15°～50°，封堵区域百分比S取值范围为0～80%，各变量在取值范围内连续变化，且各变量之间存在交互影响，采用传统试验方法须依据经验对各变量调整并进行大量试验验证。本文中通过引入中心组合设计方法［22］，通过二次多项式回归方程建立 L－θ－S的三因素传动轴护套温度预测模型，实现对传动轴护套表面温度的预测。

以L、θ和S为试验因素，采用Design Expert软件进行中心组合试验设计，取无量纲 rn＝1.682［23］，各因素及其水平见表3，针对每组试验设计进行整车试验，试验过程中测点位置与原始方案保持一致，结果见表4。

3.2 温度场优化分析

对试验数据进行多项式回归拟合，建立基于导风板与传动轴护套距离L、导风板与气流角度θ和封堵区域百分比S的传动轴护套表面温度T预测回归方程：

对上述结果进行方差分析，F值为24.05，P＜0.0001，表示拟合水平良好，自变量与因变量间有极显著的相关关系。多项式模型方程的拟合程度和模型质量由确定系数R2表示，本试验中R2＝0.9558，调整确定系数R2Adj＝0.9161，表明回归模型方程与试验数据拥有95.58%的符合度，能够解释91.61%的变化效应，对响应值的预测能力优秀，可信度较高［24］。

表4 试验设计与结果

在上述二次多项式回归方程进行响应面分析的基础上，为获取传动轴护套表面温度最低值，利用Design Expert软件的Numerical Solutions功能求取拟合方程中的响应值T的最小值，得到各参数最佳取值为：L＝25 mm、θ＝45.6°、S＝80%，此时 Tmin＝115℃［25］。

模型中各参数对风量的影响如图9所示。由图可见，传动轴表面温度随L的增大而升高，随θ的增大先降后升，随S的增大而降低，与图7描述的传动轴护套周边空气流速随几何参数的变化趋势一致，进一步验证了本文中通过增大护套周边风速来达到降低护套表面温度的正确性。其中L、θ和S三因素对护套表面温度影响的大小顺序为：L＞θ＞S，该结果与灵敏度分析结果一致。

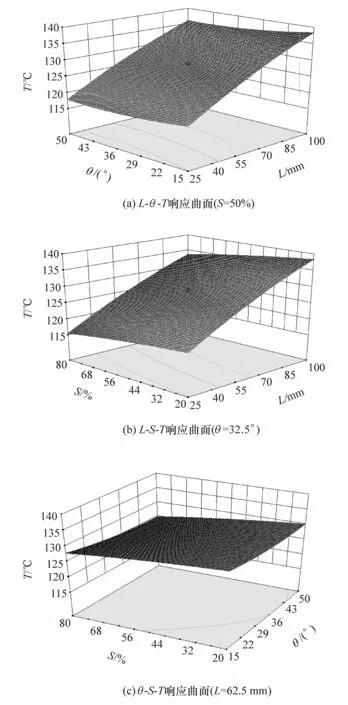
图9 模型响应曲面分析图

4 优化方案验证

4.1 优化方案的仿真验证

依据前面分析的最佳优化方案，取L＝25 mm、θ＝45.6°、S＝80%建立仿真模型，对传动轴附近气流状态进行仿真分析，结果见图10。由图10可知，采用优化方案后，气流经导流板快速流向传动轴，大幅提升了传动轴附近气流速度。进一步分析传动轴护套表面温度可知，优化后的护套表面温度降低至115.5℃（见图11），与护套表面温度预测模型计算值吻合，满足护套表面温度限值要求，证明该优化方案有效。

图10 传动轴附近气流云图

图11 传动轴表面温度云图

4.2 整车环境舱试验验证

为进一步验证优化方案的最终效果，依据最终优化方案试制了前端换热模块密封板和下导流板，并开展发动机舱温度场试验，试验过程中测点位置与仿真分析和原始方案保持一致，见图12。

图12 最终方案实物图

温度场试验设备主要包括：高温环境舱、底盘测功 机 （规 格：4*4performance／4*48″CD／4*220DW）、数据采集系统（安捷伦Agilent34972A）和压力变送器（HUBAO 40bar）等。试验工况与原工况保持一致，图13为体现试制件的整车温度场试验现场。

图13 整车温度场试验现场

原方案试验值、优化方案理论分析值和试验值见表5。由表5可知，优化方案试验值与理论分析值相差3℃，在允许误差范围之内，可认为试验值与理论分析值一致。优化后的传动轴护套表面温度为112℃，相比原试验值降低了31℃，满足传动轴护套表面温度限值，有效地解决了传动轴护套表面温度超标问题。

表5 各方案分析值对比 ℃

5 结论

本文中以整车热管理试验开发过程中遇到的传动轴护套表面温度超标问题为例，对整车开发过程中发动机舱零部件温度超标问题进行了探究，提出了“仿真分析-灵敏度分析-中心组合设计-仿真与试验验证”的分析流程，为系统全面地找出发动机舱温度场问题主要影响因素并确定各因素水平在一定范围内的最优值提供了理论基础。