智能网联环境下的多车协同换道策略研究*

刘志强，韩静文，倪 捷

（江苏大学汽车与交通工程学院，镇江 212016）

前言

据欧盟数据统计［1］，由换道导致的交通事故约占总交通事故数的5%，并带来极大的交通延迟。与此同时，75%的换道事故是由于驾驶员识别失误导致的，即对自车状态信息及周围环境感知不足。近年来随着传感器技术、车车通信技术在汽车上的应用，车辆与车辆或道路设施之间的互联正在成为现实。在网联环境下，行驶路段周围车辆信息的获取能帮助车辆制定更优的换道控制策略，从而改善换道过程中车辆的运行速度和车头间距等微观交通流特性，提高车辆驾驶的安全性和舒适性［2－3］。

自动换道的研究分为单车自动换道和多车协同换道控制。前者主要研究单车换道轨迹规划和轨迹跟踪控制；后者研究相对较少，目前关于多车协同换道策略的概念可分为目标车道前后车加减速协同和多车道多车换道协同两类［4－8］。前者定义为，不具有换道意图的协同车辆在协同过程中必须通过控制自身的运动状态来配合完成换道；后者定义为，在多车道多车情景下多车同时换道的协同行为［8－10］。日产汽车的 Cao等人［7］采用模型预测控制（model predictive control，MPC）对合流区的车辆运动轨迹进行优化，将协同行为简化为包含合流车辆和原车道合作车辆的协同模型；吉林大学的谭云龙［9］研究了快速路合流区的车辆协同换道模型，结合驾驶员特征建立了模型决策框架；德国宇航中心的Heesen等人［10］通过试验研究了实际换道中，驾驶员可能采取的协同行为，并用逻辑模型进行了回归处理。

上述研究主要是基于自动网联汽车进行多车协同驾驶的系统结构设计，对自车控制算法和周围车辆协同控制算法研究相对较少；研究场景较单一，主要集中在合流区和十字路口，不能解决实际情况下复杂交通环境的问题。另外，由于避撞约束的维度和车辆运动学的非线性，优化控制函数通常难以求解。

据此，本文中提出一种集中决策与分布控制的多车协同安全换道策略。首先提出一种基于激励函数的换道收益函数模型，判断当前交通状况是否适合进行协同换道操作。其次提出一种基于模型预测控制的协同换道优化控制模型，实时获取各车的期望控制输入量。选取美国NGSIM开源交通数据库中一个典型时段路段场景，在Matlab中应用协同策略进行仿真，验证该方法在提高交通效率与稳定性和行车安全性与舒适性方面的效果。

1 多车协同安全换道系统架构

本文中所研究的多车协同换道场景如图1所示。SV（自车）为换道车辆，ALV和AFV分别表示目标车道上的前、后车辆，LV表示同车道上前车。换道过程为SV从当前车道换道至目标车道的前车和后车之间。换道过程中，ALV、AFV和LV通过加减速配合SV完成换道，实现安全、高效驾驶的目标。其中，通过车联网环境实现换道过程中信息交互，获取的车辆状态参数均以自车为参照物。

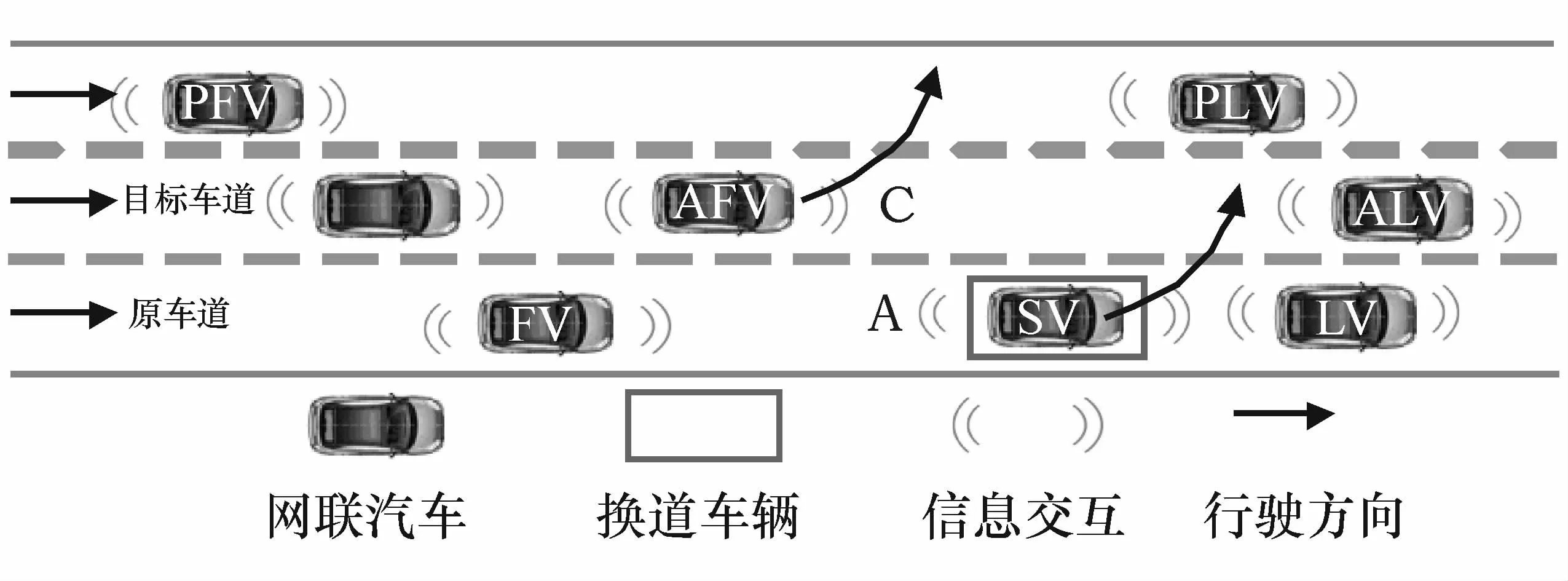
图1 协同换道场景图

为充分利用道路条件，实现系统合作的架构如图2所示。其中，智能传感层对车辆状态参数和环境信息进行感知；协调层制定协同换道驾驶策略和控制目标；车辆控制层根据协同驾驶策略的反馈，利用执行机构对油门开度、制动压力和转向盘转角进行控制；车车、车路通信技术负责车辆间信息的传递和共享，最终达到完成协同驾驶任务的目的。

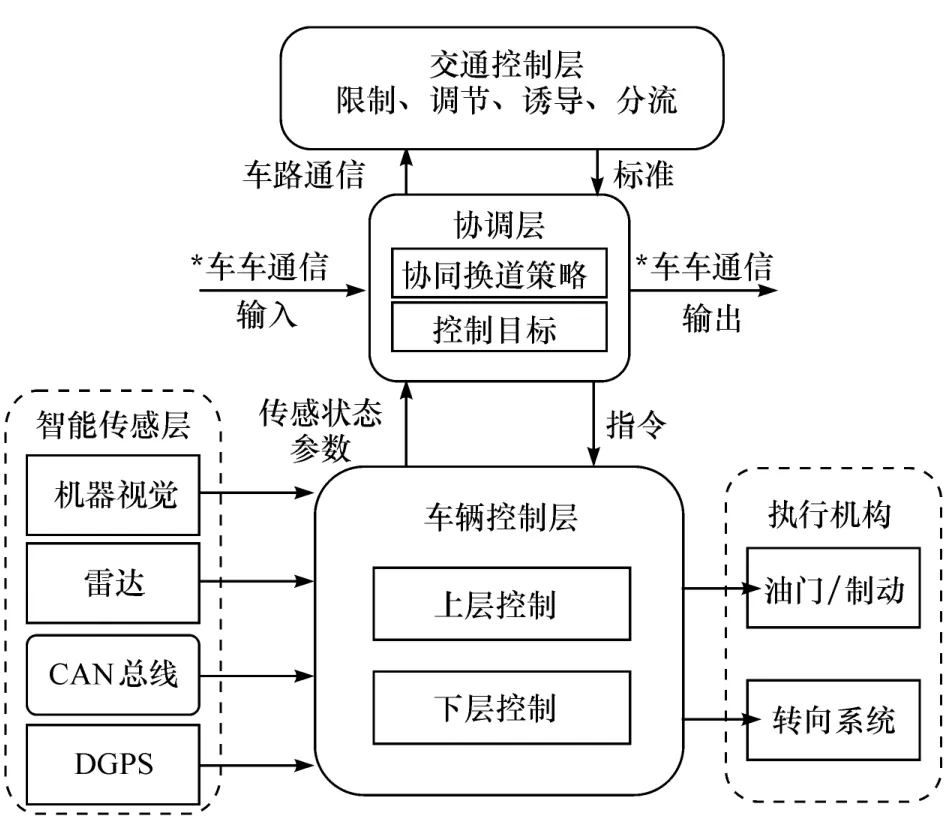
图2 多车协同换道系统架构

多车协同换道系统工作流程如图3所示。通过信息感知获取车辆状态参数和道路信息，构建换道收益函数，综合评估当前时刻协同换道行为对交通状况的获益程度，进行协同换道可行性集中决策；根据判断结果建立多目标协调优化控制模型，制定多车协同换道策略；基于换道策略获取各协作车辆的期望控制输入量，通过通信技术实现信息共享；协同换道结束后通知各车停止协作，否则继续执行协同操作。

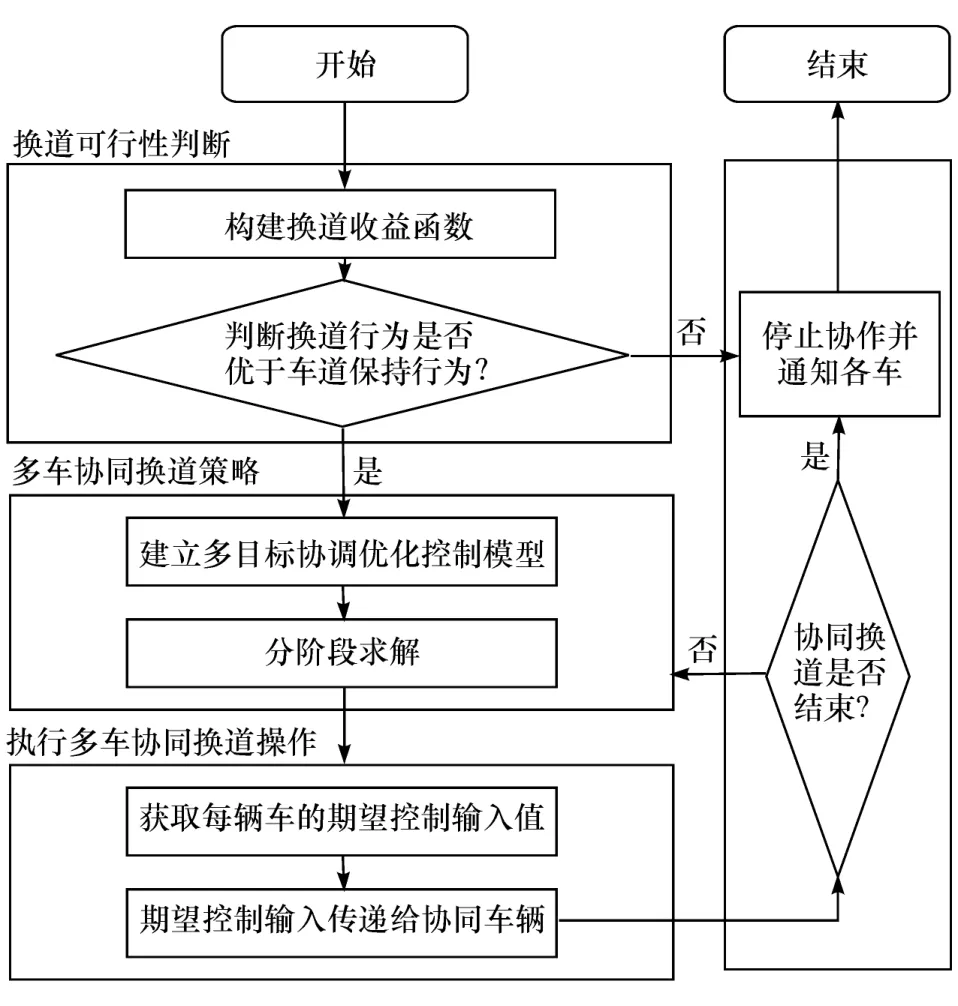
图3 多车协同换道流程图

2 多车协同换道场景

2.1 可行性判断

由于换道行为对原车道和目标车道的上、下游车辆都会造成影响，故须容纳来自多个周边车辆的信息进行换道可行性判断。为了对协同换道集中决策行为进行建模，在激励模型（incentive-based model，IBM）的基础上定义换道收益函数，以判断换道操作的获益程度［11］。换道车辆SV的候选决策生成模型公式定义如下：

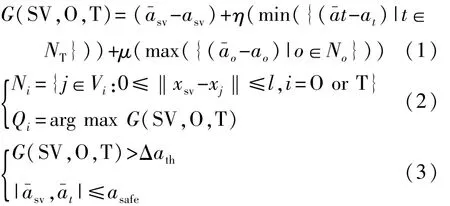
式中：O和T分别为自车SV当前车道和目标车道；G（SV，O，T）为在协同情况下，SV从 O换道到T的总体收益；NO和NT分别为在通信车道范围l内，当前车道上的后续车辆和目标车道中的后续车辆；Δath为切换阈值，表示当前交通条件下车道变换行为优于车道保持行为；a为车辆当前状态下的加速度，a－为自车换道后车辆的加速度，由下节的状态预测模型计算得到。

当且仅当收益函数G满足式（3）条件时，系统决策为协同换道可行，对于 G（SV，O，T）的计算，公式右半部分第1项是自车SV通过换道获取的速度优势。第2项中，η为礼貌因子，表征换道操作对目标车道中后续车辆（通信范围内）NT的影响，旨在减少不必要或激进的换道行为，避免破坏交通稳定性。a－t－at计算结果总是非正的，其最小值代表换道行为的最大影响。第3项中，μ为受益因子，表示当前车道上的后续车辆NO因自车换道获得的速度优势，表征换道行为对交通效率产生的积极影响。a－o－ao计算结果总是非负的，因此选择其最大值表示最大影响。

即总体收益G（SV，O，T）是由自车SV的速度收益、目标车道后续车辆NT的整体交通稳定收益和当前车道后续车辆NO的速度收益组成。

2.2 状态预测模型

为获得主车换道后各车辆的加速度，选取优化速度模型（optimal velocity model，OVM）作为车辆跟驰模型。该模型不仅能反映驾驶员特性，而且能描述交通流特性［12－13］，如式（4）所示。

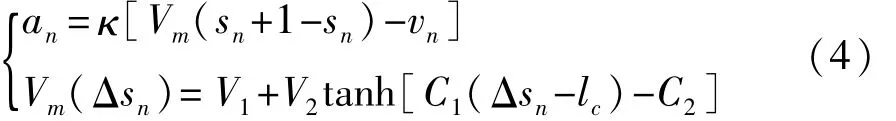
式中：an为车辆纵向加速度；sn＋1－sn为两车间的车头间距；Vm（sn＋1－sn）为优化速度函数；lc为包含车身长度的最小安全车距；V1、V2为常数参数；C1、C2为对应系数。各参数的取值可参考以往研究中的数据［13］。

3 基于MPC的协同换道策略

为实现安全、舒适、高效的换道目标，建立多目标协调优化控制模型［14］。为降低最优控制量的求解难度，将整个换道过程分为两个阶段。第1阶段为稀疏纵向间距阶段，使协同换道车队从原来的形态转移到一个足够稀疏的形态，以避免碰撞；第2阶段为换道阶段，该阶段从稀疏队形开始，车辆间的安全距离得以满足，因而可降低避免冲突的约束要求。

3.1 稀疏纵向间距阶段

第1阶段在换道开始前，调整换道车辆与前后车之间的纵向间距，使车辆间距离足够稀疏。假设每辆车都是矩形，当且仅当车辆的4个拐角不碰到路障时，才能避免碰撞。如图4所示，假设4个拐角点的坐标为（xAi，yAi）、（xBi，yBi）、（xCi，yCi）和（xDi，yDi）。根据三角形面积准则［15］可得两个不规则放置的矩形之间的避碰条件，从而将车辆之间的避碰约束公式化为

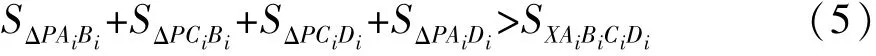
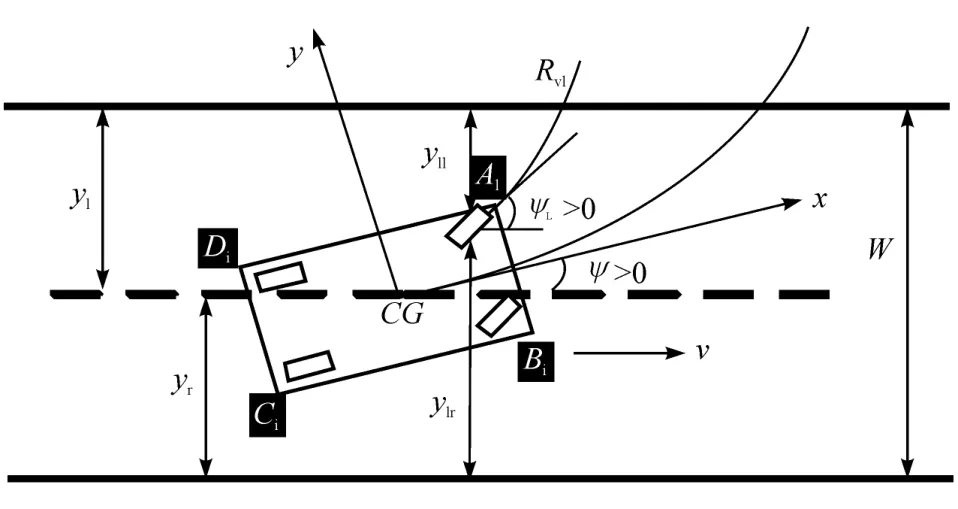
图4 车辆运动学示意图

式中：SΔ为三角区域面积；SX为矩形区域面积；P∈｛Aj，Bj，Cj，Dj｝，i，j＝1，2，…，Nv（i≠j），Nv为通信范围内的车辆数。

对自车、原车道前车和目标车道前、后车的加速度误差进行优化，保证其纵向驾驶舒适性，该阶段目标函数为

式中：N为预测时域；μ＝｛SV，FV，ALV，AFV｝；ωμ为权重因子；amin、amax为驾驶员可接受的最小、最大舒适加速度；aSV′＝aSV（k＋i＋1｜k）－aSV（k＋i｜k）为车辆的加速度变化率；Tp为驾驶员可接受的最大舒适纵向加速度变化率，加速度变化太大同样会引起驾驶员的不适。

3.2 车道变换阶段

第2阶段由稀疏队形开始，因此可降低避撞约束条件的维数，减小模型求解的难度，提升计算速度。对自车与周围车辆的加速度和跟车车距误差进行优化，表征换道过程中的舒适性代价和跟踪性代价，该阶段目标函数为

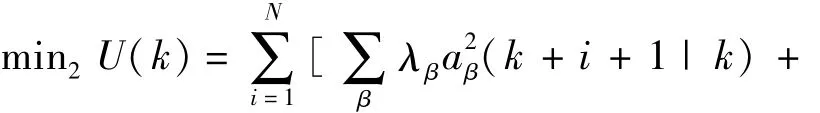
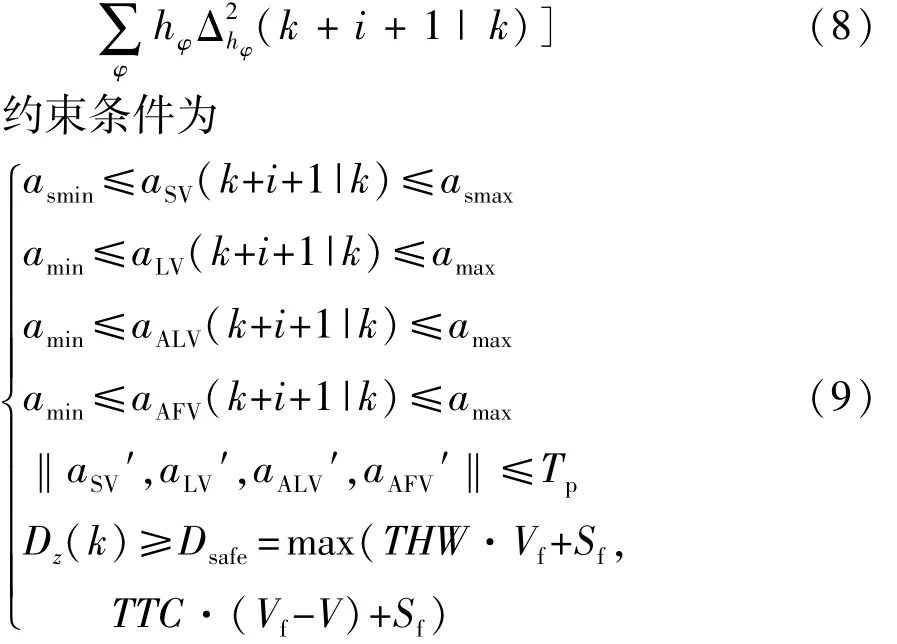
式中：hφ、λβ为各项的权重因子；（k＋i＋1｜k）为基于 k时刻的信息对k＋i＋1时刻的值进行预测；β＝｛SV，ALV，AFV｝；φ＝｛SV，AFV｝；asmin、asmax为驾驶员可接受的最小、最大舒适换道加速度；Dz（k）为k时刻两车之间的实际距离，且 z＝｛SV－ALV，SV－AFV｝；THW为两车间的安全临界跟车时距；TTC为安全临界碰撞时间；Vf为前车速度；Sf为最小安全车间距。

式（9）前5式保证了换道过程中各车的安全性和舒适性，确保状态控制变量在容许范围内，式（9）最后一式表示两车间的距离满足最小安全距离。

在车道变换阶段，SV的纵向加速度随期望的控制输入量而变化，采用如式（10）所示的正弦函数表达横向加速度 ay（t）［16］：

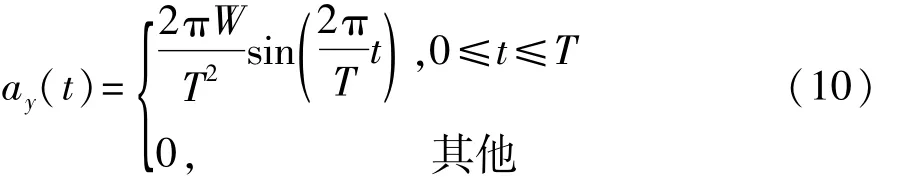
式中：T为整个换道过程横向移动持续时间；W为车道宽度，即需要完成的横向位移。

根据换道横向加速度可得到横向位移的变化：

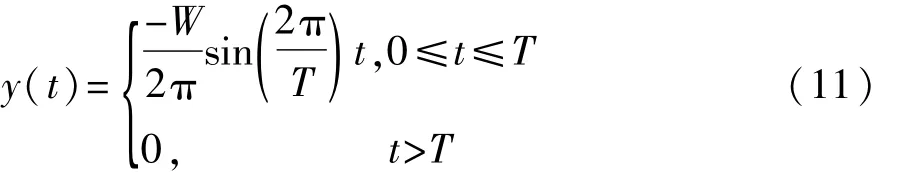
当换道车辆的横向位移达到车道宽度W时，即可视为完成换道阶段，如图5所示。

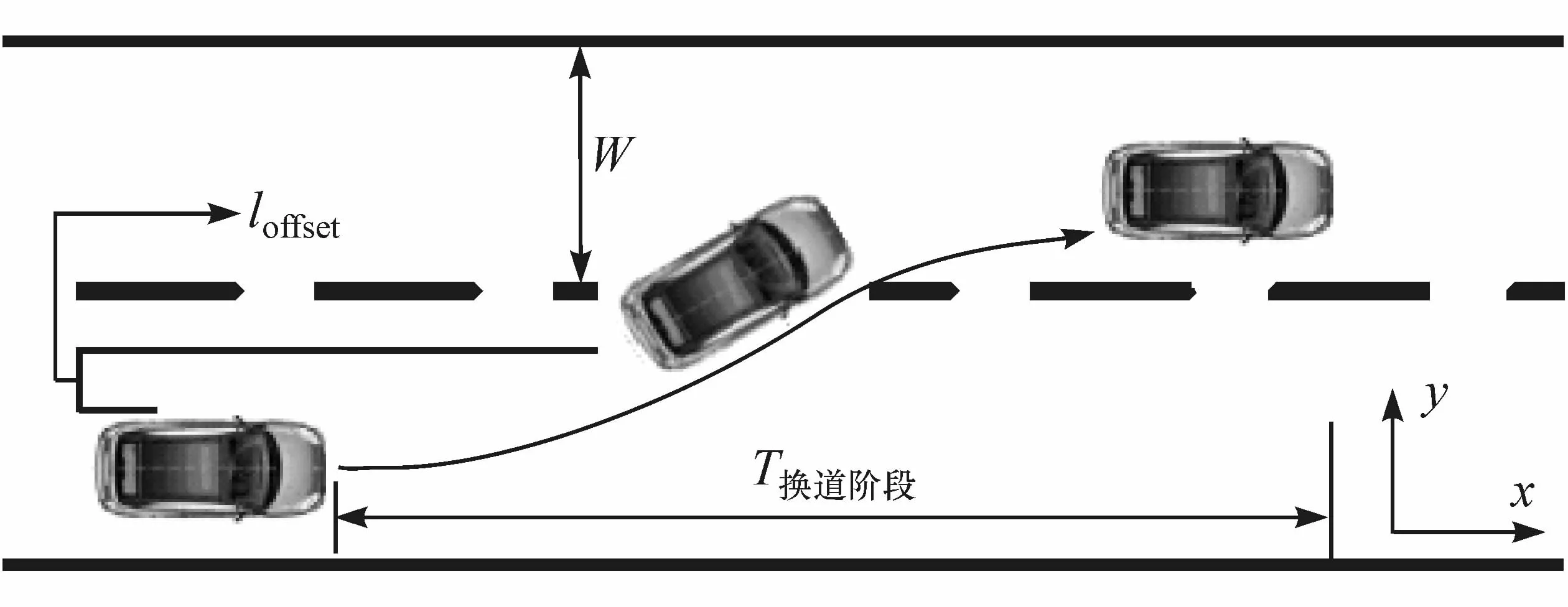
图5 SV换道过程

3.3 问题求解

由于本文中所建立的目标函数为多目标协调优化控制问题，故采用滚动时域优化算法求解该问题。即随着采样时刻的推进，在滚动的有限时间区间内反复对每一时刻的偏差进行优化计算［17］，得到控制阶段各车的期望输入从而实现主动协作。系统预测时域内，约束条件均为AX≤B的形式，因此采用约束管理法软化硬约束。选择Dantizig-wolfe有效集法［18］求解多目标协调优化控制问题，得到最优控制变量：

约束条件如式（7）和式（9）所示。

提取最优控制量的首个元素X（0），将其输入自行车的车辆模型中，得到期望的最优油门开度c*thr（0）和最优制动踏板压力c*brk（0），实现对车辆驱动和制动的优化控制。模型中的参数取值见表1。

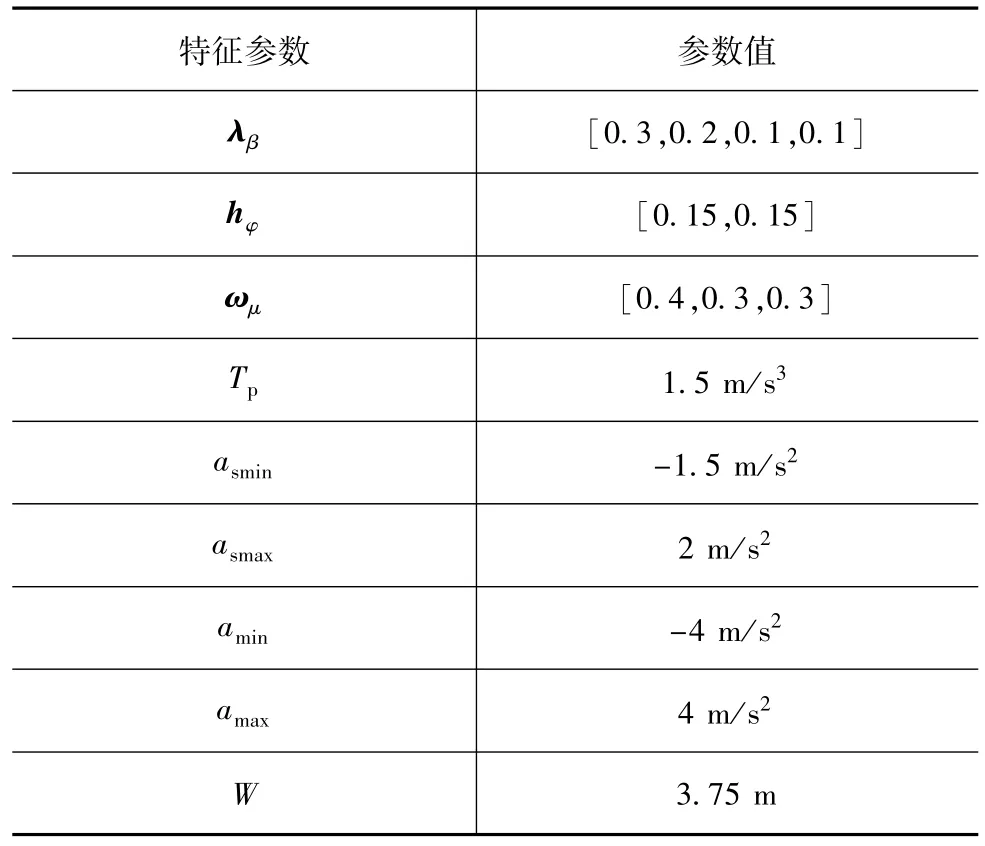
表1 多目标协调优化控制策略的特征参数及数值

4 仿真验证

4.1 仿真场景

本文中基于美国NGSIM开源交通流数据［19］，采用Matlab／Simulink联合仿真，对模型进行验证。该数据源利用图像处理技术提取并开放了车辆的运动轨迹数据。选取数据库中101高速公路上某路段交通数据进行分析。该路段全长约640 m（2 100 ft），如图6所示。将选定时刻内自然驾驶行为下的实际换道场景定义为一般传统换道（general lane changing，GLC）；将应用多车协同换道策略后的仿真换道场景定义为协同换道（cooperative lane changing，CLC）。

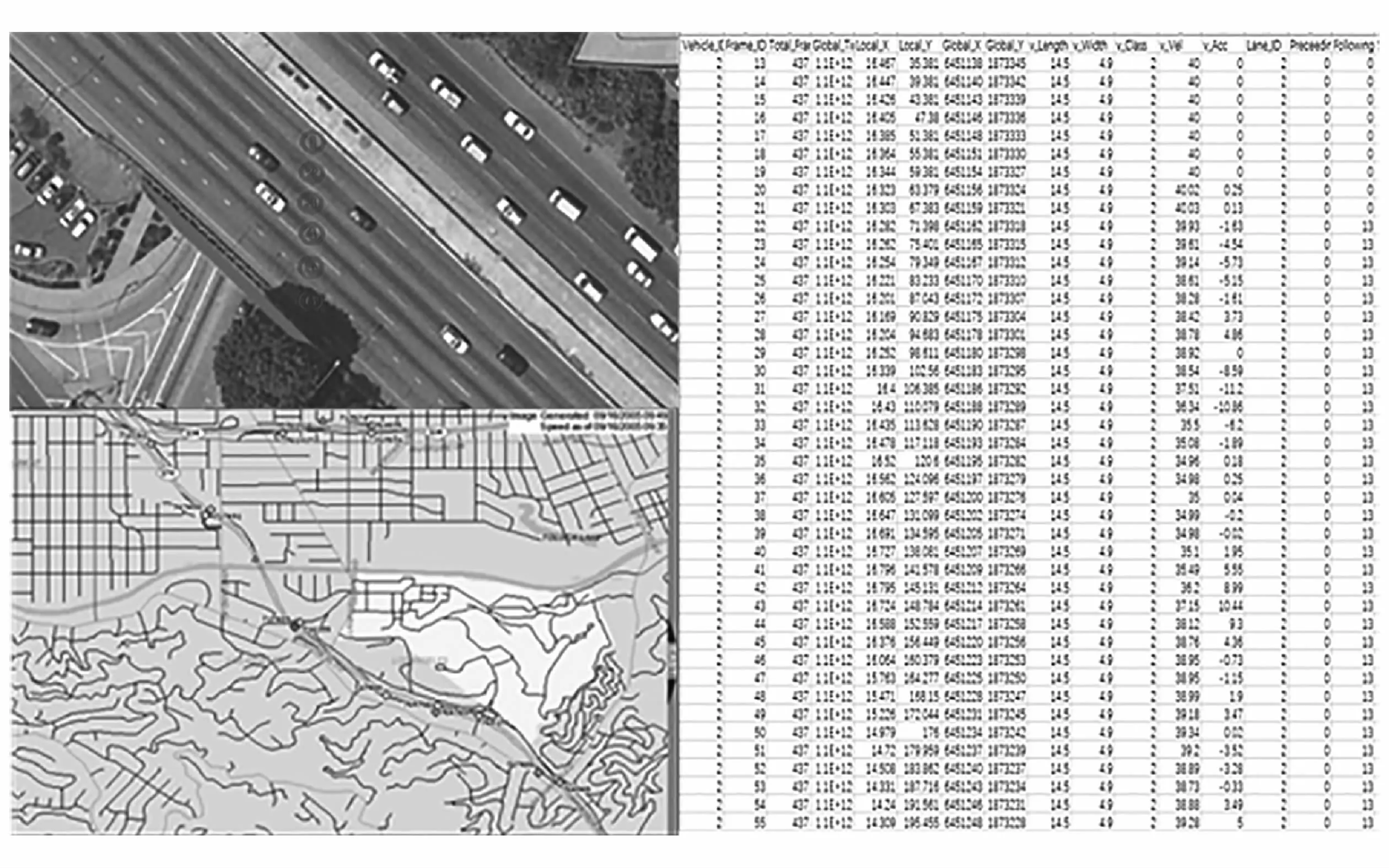
图6 选取的高速路场景

一般传统换道的结果是车辆在该路段第4、5车道上8：05－8：20 am期间的行驶数据和统计分析，并以此作为验证所提策略的参照结果。协同换道结果是基于上述场景，在相同工况下使用多车协同换道策略，对换道过程进行仿真得到的车辆运行数据。

通过比较两种情形下换道过程中局部交通系统的性能指标和车辆运行参数，验证所提策略的有效性。

4.2 结果与分析

图7为传统换道场景下的车辆运行轨迹图，选取路段该时段内共发生6次换道行为。图8为应用多车协同换道策略后的车辆运行轨迹图。对比图8和图7可见，车辆速度区间值提升，车辆行驶到相同位置的时间缩短，道路通行效率提高。另外，在该场景中评估传统换道和协同换道情况下所有可行的换道数量，在CLC场景下可实现的换道数量提升至10次。换道可行性的增加相对不明显，这是由于验证场景所取路段较短，且处于自由流状态的车辆较多所致。

本场合的平均车速是指一定时间或空间范围内所有车辆速度的平均值，包括时间平均车速和空间平均车速，是评价交通系统的重要性能指标。图9为一般换道和协同换道情况下各时间段内时空平均车速，协同换道策略下车辆的时间平均速度最多可由11.79提升到14.31 m／s，空间平均速度最多可由9.86提升到12.05 m／s，平均车速得到明显提升。

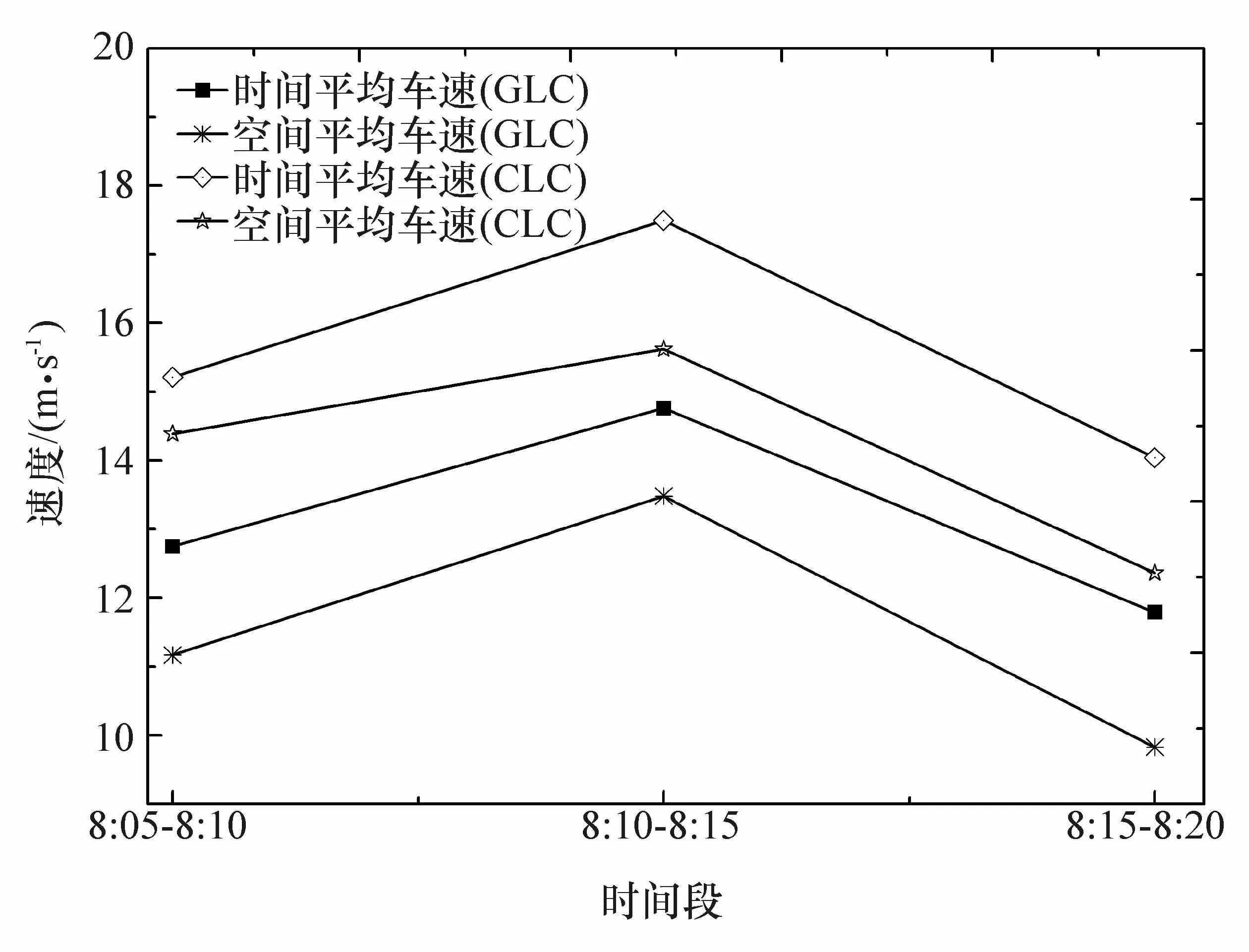
图9 两种情况下的时间、空间平均速度

稀疏纵向距离阶段第1辆换道车辆的实际加速度与期望加速度曲线如图10所示。CLC场景下各车实际加速度接近于驾驶员期望加速度，且加速度变化率在驾驶员可接受的范围内，表明多车协同换道策略符合驾驶员的操作习惯且满足舒适性要求。

换道车辆的行驶轨迹如图11所示。由图可见，换道轨迹各个点的位移、速度和加速度曲线光滑连续，换道过程平稳。

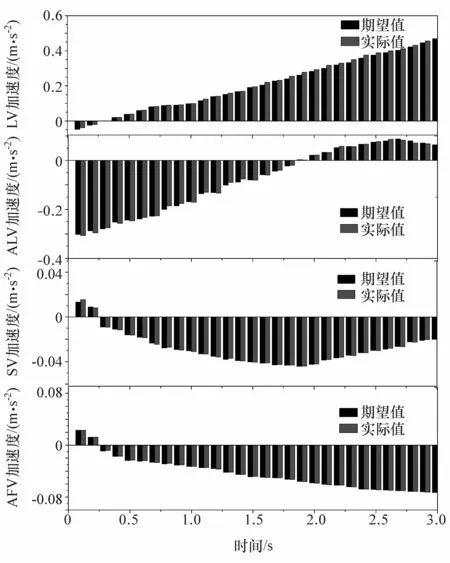
图10 第1阶段各车加速度（CLC）

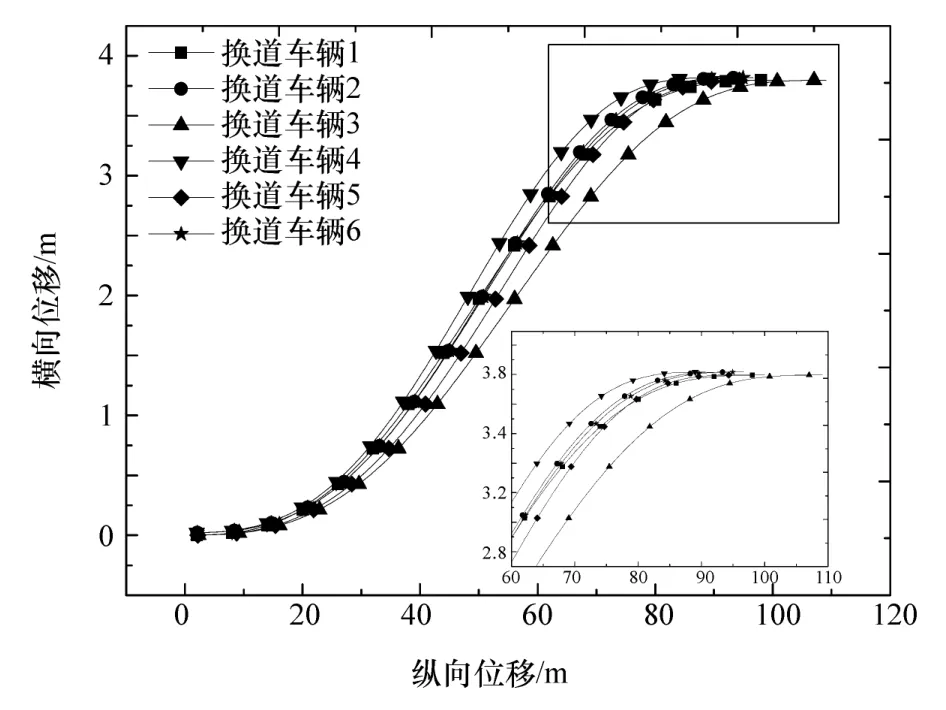
图11 换道轨迹图

换道阶段换道车辆和周围各车的加速度如图12所示。设定换道前，换道车辆SV以相同的速度匀速行驶，换道过程中各车的速度变化率均在驾驶员可接受的舒适加速度范围内。图12（a）为协同换道场景下换道车辆SV在换道阶段的加速度变化情况。换道车辆的加速度变化趋势为先减速后加速，加速度变化平缓。图12（b）为协同换道场景下目标车道前车ALV在换道阶段的加速度变化情况。图中第1个交点为换道车辆1与换道车辆5在3.6 s左右加速度达到相同值，即车辆1的加速度变化率大于车辆5的加速度变化率。场景设置中，车辆1与前车的车间距为16 m，小于车辆5与前车的车间距（22 m），目标车道前、后车根据当前环境信息调整自身行驶状态。图12（c）为协同换道场景下目标车道后车AFV在换道阶段的加速度变化情况。图中4.7 s左右各车加速度均近似逼近于0。参数设置中，目标车道后车与换道车辆之间的车间距接近最小安全距离，因此在安全性得到满足的前提下，令各车的纵向加速度以驾驶员可接受的最大舒适纵向加速度变化率变换至期望目标纵向加速度后匀速行驶，并使目标函数U（k）达到最小值。

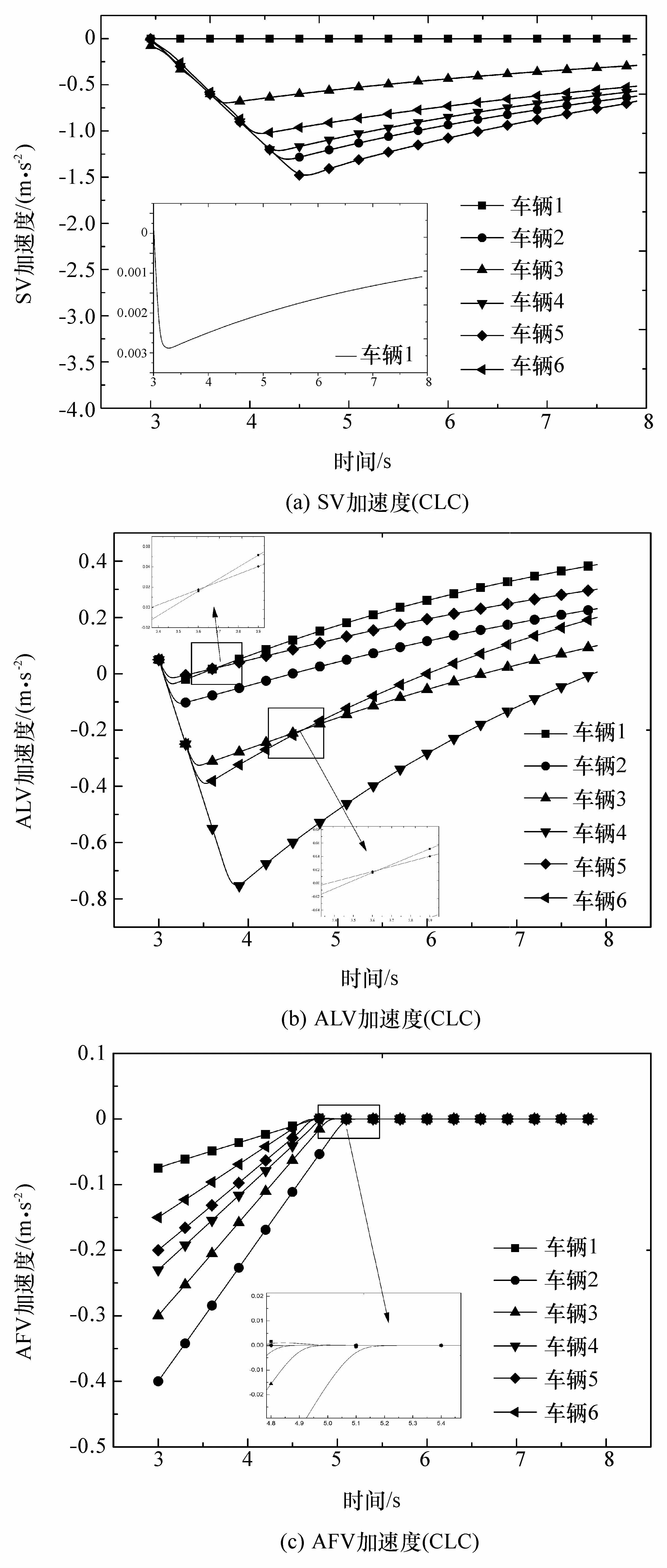
图12 第2阶段各车加速度（CLC）

5 结论

本文中基于全面实时的多车信息，充分考虑自车换道过程中周围车辆的主动合作，相对于一般换道，为驾驶员提供更为舒适的驾驶体验。本文中提出的基于集中式决策和分布式控制的多车协同换道MPC策略将整个换道过程划分为稀疏纵向距离阶段和车道变换阶段，减小了优化控制模型的求解难度。通过美国NGSIM开源交通流数据库中的实际交通场景对CLC策略和GLC策略进行了比较，得到如下结论。

（1）与一般换道相比，协同换道策略能提高车辆换道的可行性；且交通流中的冲击波可得到一定程度的缓解，上游车辆的减速度减小，降低了换道对目标车道车辆的消极影响。

（2）在协同换道过程中，车辆的平均速度提升20%～25%；各车加速度变化趋于平稳，换道过程更加安全高效，道路通行效率提高。

（3）本文中研究忽略了通信延迟或传感故障，将在今后的工作中加以考虑，并根据配备协作装备的车辆现场数据进一步设计相关的控制策略。