LS+AR单差模型预报极移参数方法研究

郭忠臣，孙 朋，李致春

宿州学院环境与测绘工程学院，安徽宿州,234000

极移在卫星导航、大地测量等领域具有重要作用，但当前观测技术并不能实时获得高精度极移观测量[1]。为了实时得到高精度极移观测量，越来越多的方法被应用到极移预报中，当前主要有最小二乘外推法(Least squares extrapolation model)、神经网络模型(Neural networks)、卡尔曼滤波(Kalman filter)和最小二乘联合自回归模型(Least squares extrapolation of the harmonic model and autoregressive prediction，LS+AR模型)等[2-6]。地球自转参数预测方案比较大会战(EOP PCC)活动证实没有任何一种方法适合所有跨度的极移预报，但LS+AR模型在极移短期预报方面精度较优[7]。

LS+AR模型在进行极移预报时，首先通过对极移序列构建LS模型，然后对LS拟合的残差项构建AR模型，LS模型与AR模型的预报值之和即为最终预报值。但LS+AR模型在预报时，并没有完全顾及模型与极移序列的适应性，在一定程度上影响了预报结果的精度[8]。本文从增强数据的平稳性以及与模型的适应性方面考虑，对传统LS+AR模型预报极移的方式进行改进，实验结果表明，改进后的模型预报精度较LS+AR模型具有一定提高。

1 LS+AR模型

1.1 LS模型

极移主要受趋势项和周期项影响，其中周期项主要有Chandler项、周年项和半周年项，由参考文献[9-11]可知，极移序列的LS模型可构造成：

(1)

其中,ai为趋势项拟合系数，bi、ci、di为周期项的振幅，P1、P2、P3分别为Chandler项、周年项和半周年项的周期，t为时间。

将式(1)化简成：L=BX，即可通过最小二乘原理计算参数X。

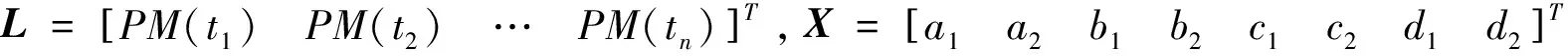
1.2 AR模型

AR模型主要针对平稳时间序列构建模型，模型适应度越高，则建模预报效果相对越好。AR模型基本形式可表示为[9]：

zt=φ1zt-1+φ2zt-2+…+φpzt-p+εt

(2)

其中,z为原始序列，φi为AR模型系数，εt为t时刻的白噪声，P为模型阶数。

使用AR模型建模时，需要合理的确定模型阶数P。当前主要有AIC准则和BIC准则等用于AR模型定阶，本文使用AIC准则确定模型阶数，当AIC(P)取最小值时，P即为最佳阶数[12]。AIC准则表示为：

(3)

2 LS+AR单差预报模型数据处理流程

本文从增强数据的平稳性以及与模型的适应性方面考虑，对传统LS+AR模型预报极移方法进行改进，改进的模型记为LS+AR单差模型。该模型的预报模式为：①对原始序列构建LS模型，得到序列的拟合参数、拟合值及残差序列，残差序列记为LS_bias，LS外推结果记为LS_pre；②对残差序列LS_bias作一阶差分处理得到LS_bias_diff；③对差分后序列构建AR模型，AR模型的预报结果记为LS_diff_AR_pre；④对LS_diff_AR_pre作逆差分，即可得到预报的残差序列LS_AR_pre，LS_pre与LS_AR_pre之和即为最终的预报值PM_pre。具体预报流程图见图1。

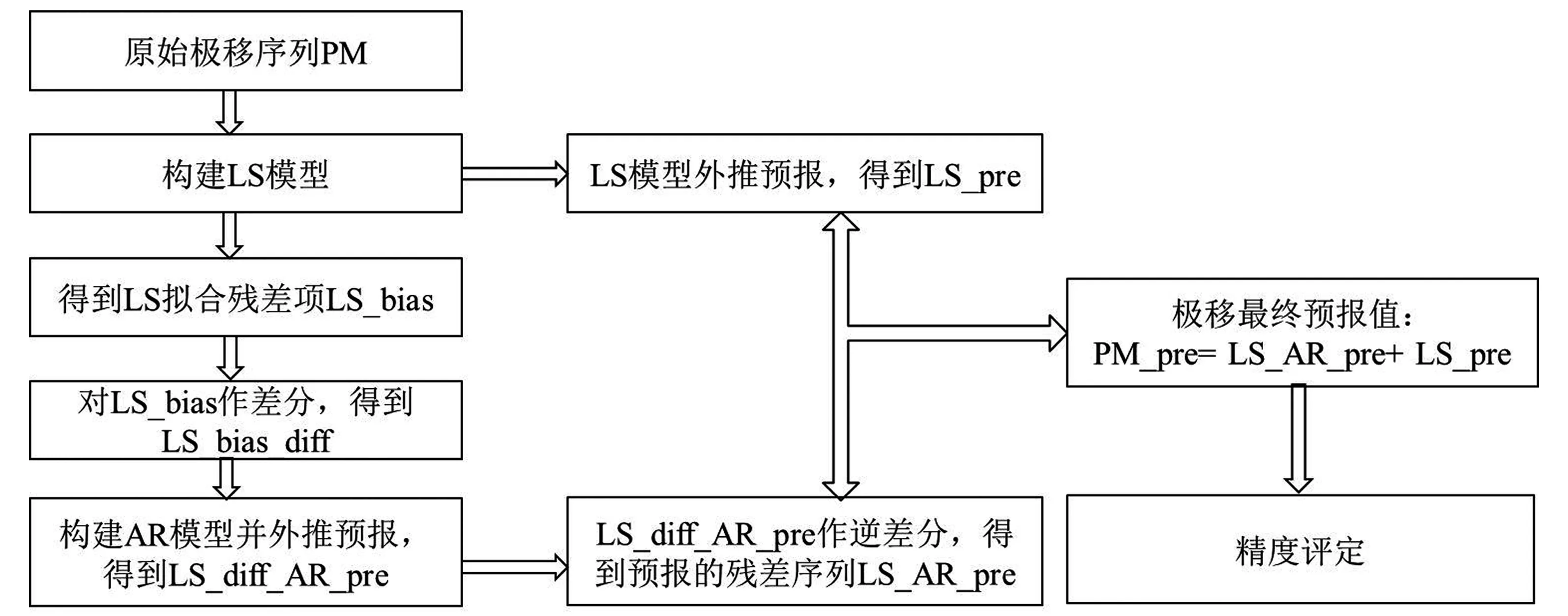
图1 LS+AR单差模型预报极移流程图

3 实验分析

实验所用数据来源于IERS公布的EOP C04序列(http://hpiers.obspm.fr/eoppc/eop//eopc04/eopc04.62-now)，数据采样间隔为1天，取2009/07/01至2020/01/01(儒略日：55013至58849)期间的数据进行实验。顾及序列内部数据之间的相关性，选取10年长度的极移序列作为基础序列，其余数据用于精度评定。

为对比单差模型的预报精度，构造如下两种实验方案：

方案一：使用LS+AR模型进行预报；

方案二：使用LS+AR单差模型进行预报。

3.1 方法可行性分析

图2给出了LS模型对实验数据的拟合结果，图3给出了LS模型拟合后的极移X方向(PMX)和极移Y方向(PMY)的残差及差分后的结果，可以看出，LS模型拟合的残差波动较大，X方向和Y方向残差分别在-0.07～0.06 as和-0.07～0.08 as之间，差分后X方向和Y方向残差分别在±0.002 5 as和±0.002 as之间，差分后残差序列波动更加趋于平稳。图4和图5分别给出了PMX和PMY残差序列及其差分后的频数分布直方图，通过假设检验可知，差分后的残差序列均符合正态分布与AR模型的契合度更高[13]。

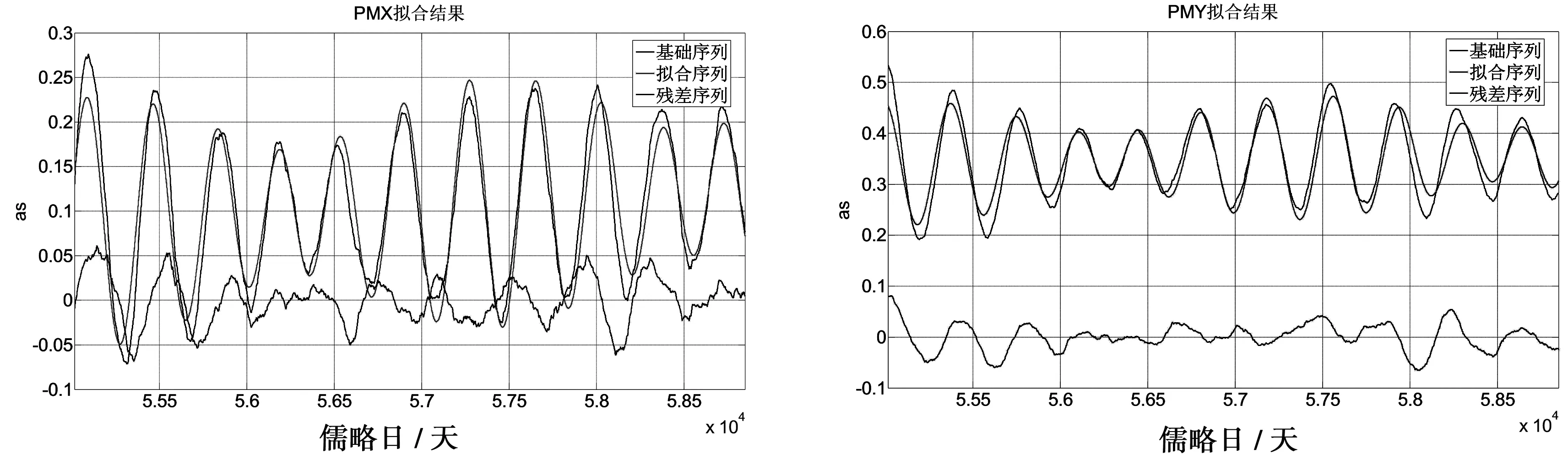
图2 LS模型极移拟合结果

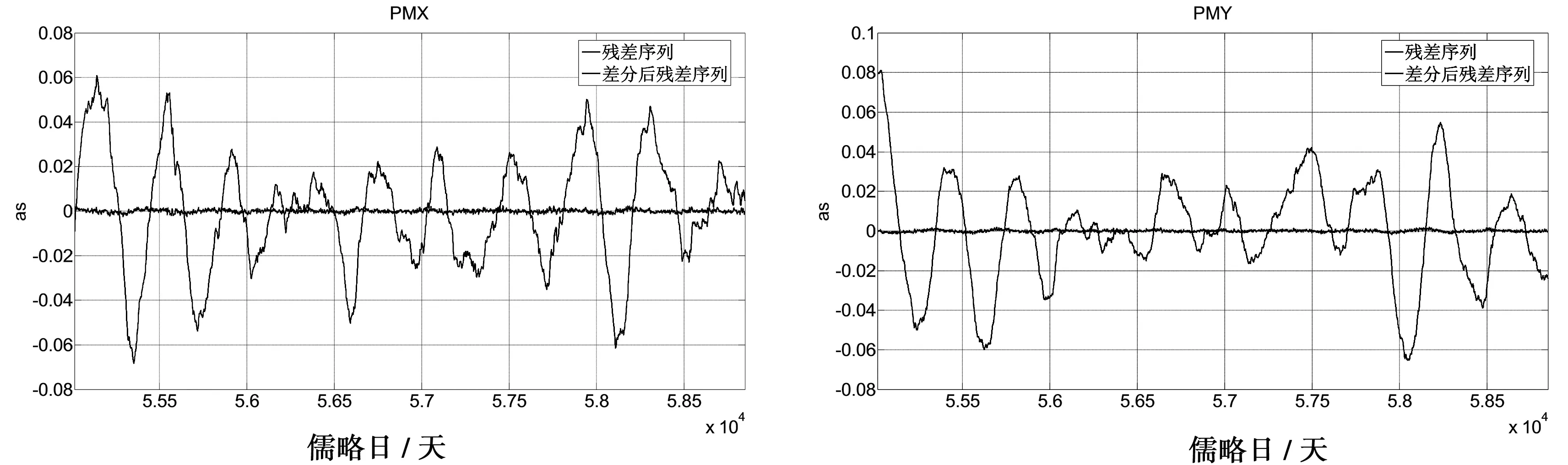
图3 极移残差序列及差分后残差序列

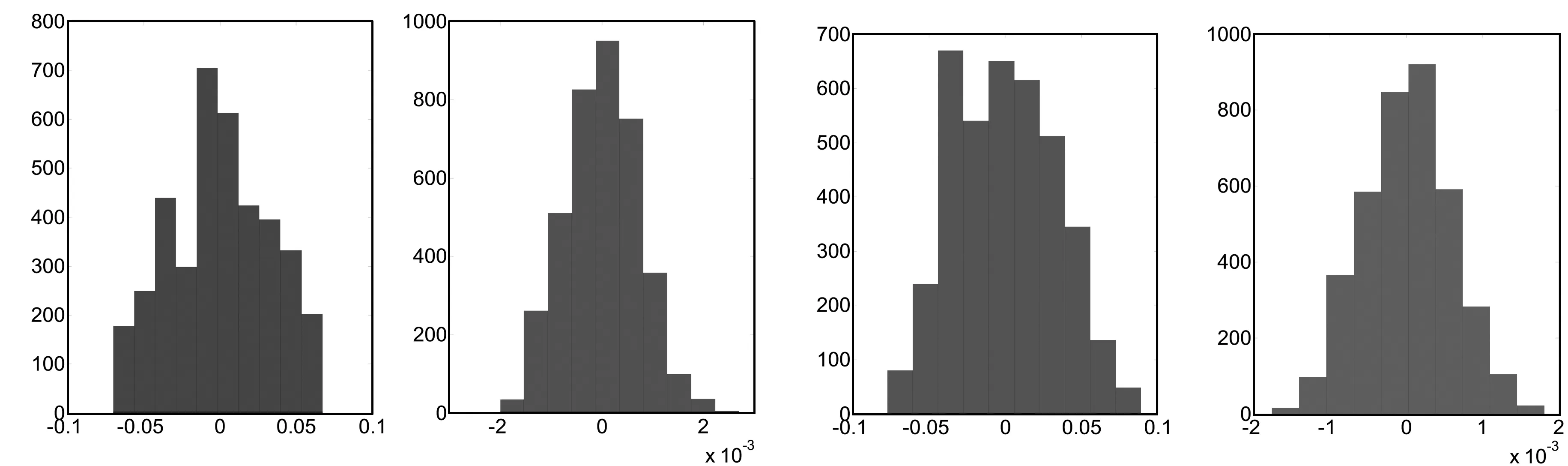
图4 PMX残差序列及其差分后的频数分布直方图 图5 PMY残差序列及其差分后的频数分布直方图

3.2 实验结果分析

分别对PMX和PMY进行1～30天的预报，不同跨度各预报60期，使用平均绝对误差(MAE)进行精度评价，MAE计算公式为[9,11]：

(4)

其中：i为预报跨度，j=1,2，…，n为预报期数，P为极移预报值，O为极移观测值。

图6和图7分别给出了两种方案PMX和PMY预报10天和30天的精度统计，图8给出了EOP PCC活动的预报结果。

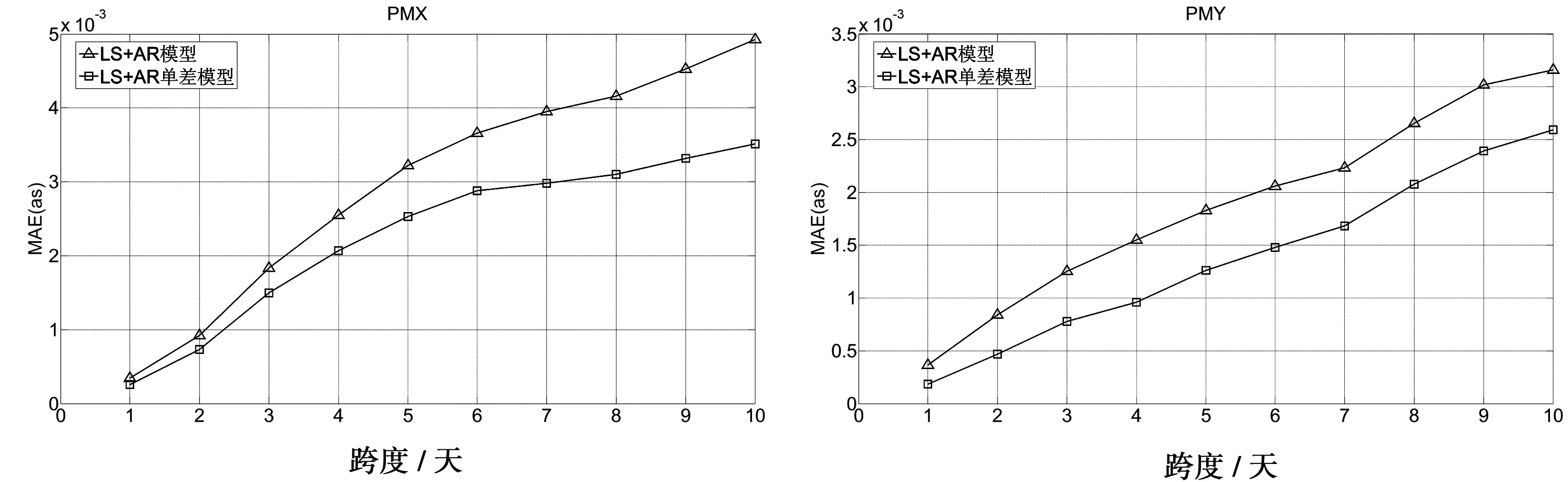
图6 两种方案预报10天精度对比

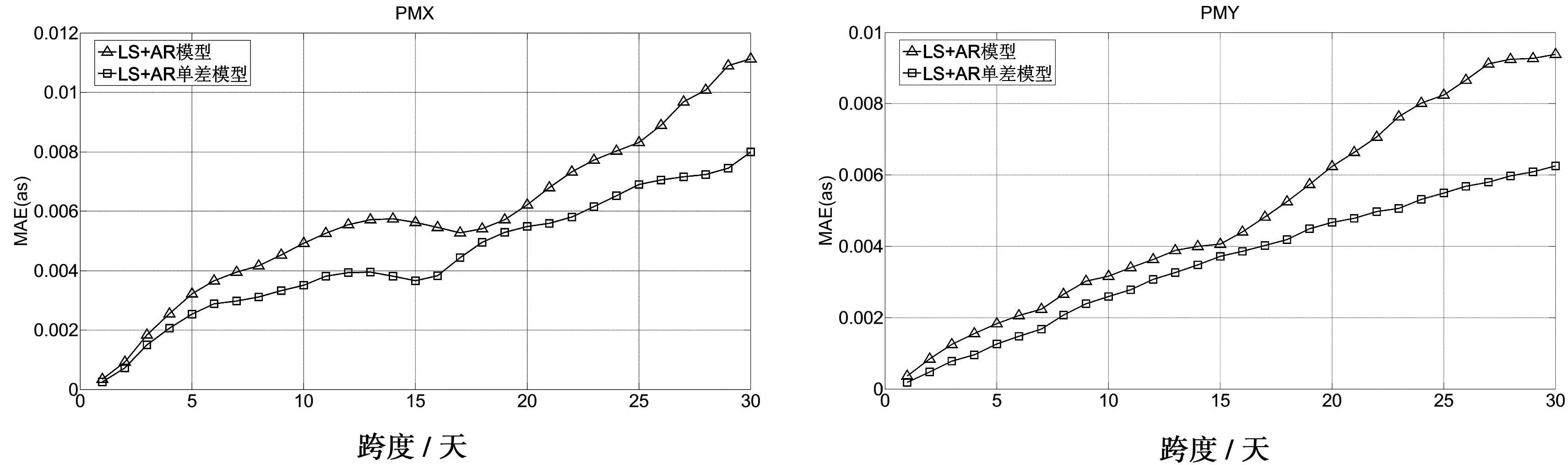
图7 两种方案预报30天精度对比

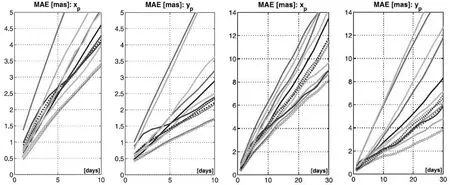
图8 EOP PCC活动预报结果

通过分析可知：

(1)在预报跨度为1天时，方案一和方案二预报的PMX和PMY的MAE分别为0.348 mas、0.254 mas和0.364 mas、0.184 mas，对于PMY预报1天的精度来说，方案二较方案一提高了97.5%，精度提高较为明显，另外EOP PCC活动预报1天的极移基本上都在0.4～1.0 mas之间，本文所用两种方案的预报精度均优于EOP PCC活动的预报结果，这也与本文所用数据的精度较高有关；

(2)随着预报跨度的增加，PMX和PMY的预报误差基本上都在逐渐增加，预报跨度为10天时，对于PMX而言，方案一和方案二的预报误差分别为4.924 mas和3.512 mas，EOP PCC活动中大多方法的预报误差在3.4～5.0 mas，方案一的预报精度与EOP PCC活动相当，但方案二的预报精度基本上高于EOP PCC活动中的所有方法；对于PMY，方案一和方案二的预报误差分别为3.162 mas和2.595 mas，EOP PCC活动中大多方法的预报误差在1.6～3.5 mas，两种方案与EOP PCC活动中的预报精度相当；

(3)在预报跨度为10～20天时，PMY的预报误差逐渐增大，PMX的预报误差出现了波动，即部分跨度的预报误差较前一跨度有所降低，对于PMX在不同跨度预报精度变化规律不一致的情况，考虑是与预报过程中AR模型阶数的选取及数据的循环迭代使用有关，后续将会进一步设计实验进行分析；

(4)预报跨度在20～30天时，方案一的预报误差增速较快，方案二预报误差增速平稳，方案二预报的PMY较方案一相比，部分跨度预报精度可提高50%以上，预报精度与EOP PCC活动中大多数方法相当，对于PMX，方案二的预报精度较方案一可提高20%～40%，但方案二的预报精度基本上优于EOP PCC活动中的所有方法。

4 结 论

本文从数据与模型的适应度考虑，对传统LS+AR模型预报极移的方式进行了改进，并将改进后的极移预报精度与传统LS+AR模型和EOP PCC活动进行对比。通过对比可知，改进后模型的预报精度具有一定程度的提高，说明改进后的预报方式具有一定的研究意义。从总体趋势来看，随着预报跨度的增加，精度提高越明显，并且PMY的预报精度提高优于PMX，另外在预报1天时，PMY的预报精度提高了97.5%，且优于EOP PCC活动中的所有方法，预报跨度为20～30天时，PMY的预报精度可提高30%～50%，PMX在预报跨度为20～30天时，预报精度基本上优于EOP PCC活动中的所有方法。