从选做题《极坐标与参数方程》看高考数学的变化

罗 红

(云南省蒙自市第一高级中学 661199)

高考是我国重要的选拔性考试，是教学的指挥棒，研究高考试题是我们一线教师和学生都应该认真做的事情.近几年高考数学试题也在不断的发生变化，以选做题《极坐标与参数方程》全国3卷为例，来看一下试题是怎么“进化”的.

一、题目问题直接，学生容易入手，得分高

2016年这道题第一问问得直接，只需要会转换方程即可，第二问考查的知识点单一，一个点到直线的距离公式就可以完成.

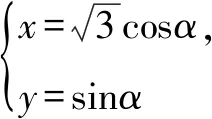
(1)写出C1的普通方程和C2的直角坐标方程；

(2)设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P的直角坐标.

解析试题分析(1)利用同角三角函数基本关系中的平方关系化曲线C1的参数方程为普通方程，利用公式ρcosθ=x与ρsinθ=y代入曲线C2的极坐标方程即可；(2)利用参数方程表示出点P的坐标，然后利用点到直线的距离公式建立|PQ|=d(α)的三角函数表达式，接着求出最值与相应的点P坐标即可．

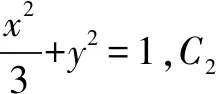
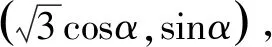
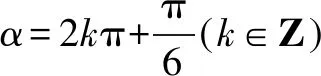
这道题属于容易题，常规题，只要学生认真学习过，训练过，那么是可以很快入手并且很容易得满分，从学生的角度来讲，遇到这样的题就该偷着乐了，所以很多学生当年都选做了这题.

二、题目问题直接，有一定的难度，入手容易解对难

2017年第一问虽然也是求方程，但是方程里还含有参数，参数是大部分同学不能理解的一个难点，比起2016年来难度有所增加.

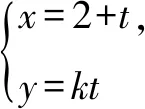
(1)写出C的普通方程；

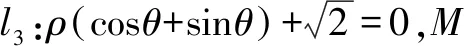
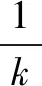
(2)C的极坐标方程为

ρ2(cos2θ-sin2θ)=4(0<θ<2π,θ≠π).

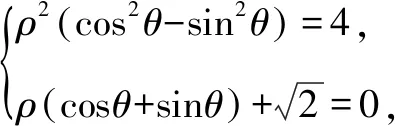
得cosθ-sinθ=2(cosθ+sinθ).

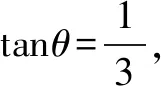
2017年这道题与2016年相比，虽然问题直接，但是里面涉及到的内容很多，学生必须学会从中提炼出关键，找到突破口，重点考查了转化与化归能力.要懂得遇到求曲线交点、距离、线段长等几何问题时，求解的一般方法是分别化为普通方程和直角坐标方程后求解，或者直接利用极坐标的几何意义求解.还要结合题目本身特点，确定选择何种方程.

这道题题目，第2问不光这种解法，学生也可以把极坐标方程改为普通方程，用普通方程把M点坐标求出，从而求出极径.

三、题目问题不常规，入手已不容易

2018年这道题难度比2017年略有增加，主要是第一问不好入手，第二问和2017年第二问基本持平.

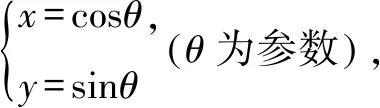
(1)求α的取值范围；

(2)求AB中点P的轨迹的参数方程．

解析(1)圆O的直角坐标方程为x2+y2=1.

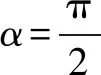
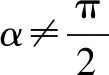
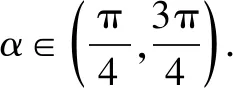
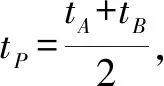
2018年这道题第一问已经不像前两年一样简单，直白，前两年第一问都是写方程，学生只需进行简单训练就可以完成，至少可以保住5分，但是今年的第一问就是参数，学生最怕的就是参数，所以第一问得分不高，第二问考查的是中点的t的意义以及求法，要考的概念虽然清晰，但在第一问的前提下，这个点也就变成了难点，所以这一年这题学生得分不高.

四、题目读不懂，无从下手

2019年与前几年相比，题目新颖，学生必须具备很强的数学阅读能力才能读懂题意，这道题也上了今年高考的热搜，考生普遍反映《极坐标和参数方程》这道选做题越来越难.

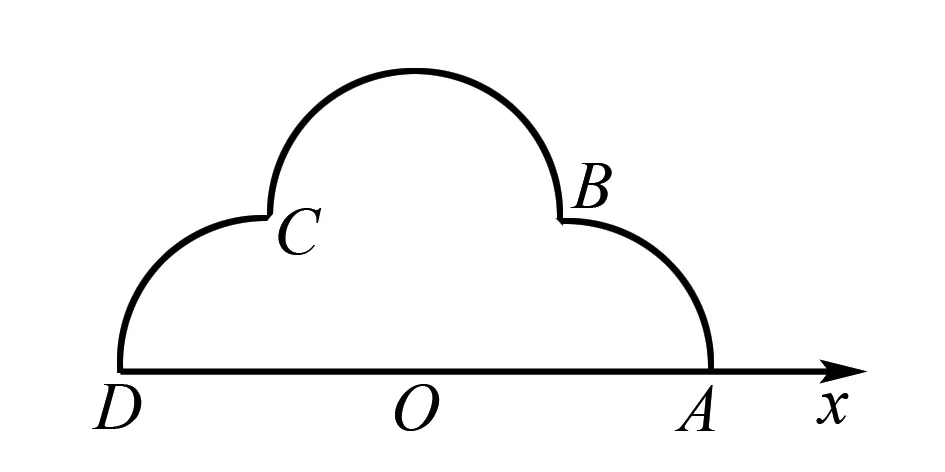
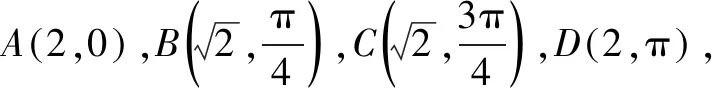
(1)分别写出M1,M2,M3的极坐标方程;

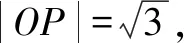
解(1)由题意可知M1,M2,M3的直角坐标方程分别为:(x-1)2+y2=1(1≤x≤2,0≤y≤1),

x2+(y-1)2=1(-1≤x≤1,1≤y≤2),

(x+1)2+y2=1(-2≤x≤-1,0≤y≤1).

所以M1,M2,M3的极坐标方程分别为

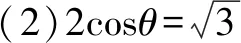
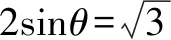
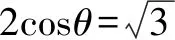
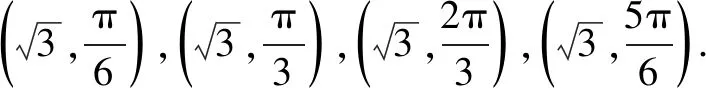
2019年这道题学生得分率极低，大部分同学连题目都读不懂，根本就是无从下手，感觉平时练了那么多题白练了，本来以为数学换汤不换药，谁知今年连碗都换了，真是刷题无数遍，败给一片云.

2019年的这道题是突然变难的吗？其实不然，觉得它难是因为没有好好研究这几年这道题的变化，题目从一开始的可以直接下手，慢慢变成需要动脑筋、多计算，再到后来的需要学生从题目中提炼出数学信息，题目考查看似知识点难度在加大，其实考查学生解决问题的能力，不再是单一的知识点的考查，是在跟现实生活接轨，要学生真正懂得数学的意义何在.从这道题的背后，我们也能看出，2019年数学试卷突出数学核心素养的考查，重视揭示数学核心概念的本质属性，强调数学实际应用和学生的生活体验，体现数学文化.

高考是教学的指挥棒，从今年的这道题目中我也在思考，在反思，给学生练了那么多，是不是每次都是针对知识点，方程的转化，t的意义，中点的运用，轨迹的求法……却缺少对试题提供的信息进行分拣、结合和加工能力的训练，这就好像在生活中，一个满身本领的人，遇到问题却不知道要用什么本领，那他学了这么多又有何用，高考是具有选拔功能的考试，数学试题的命制强调“以能力立意”.以能力立意命题，是从问题入手，把握学科的整体意义，用统一的数学观点组织材料，对知识的考查着重于理解和应用，特别是知识的综合性和灵活运用.这就要求考生善于抓住问题的本质，能对试题提供的信息进行分拣、结合和加工，寻找解题途径.这样的问题，无现成的题型、模式或方法套用，需要的是创造精神和创新意识.

长期以来数学教师在备课时已经把教材内容进行了提炼，在课堂上通过自己的语言表达给学生，而大部分学生是被动地接受和理解，学生没有进行课前预习，对数学概念的理解印象不深，时间一长容易忘记.所以，在以后的教学中我们也应该转变观念，要注重学生学习知识的体验，要有一个整体的过程体验，这就好像授人以渔，不能只教钓鱼的方法，还应该让他学着做鱼竿，学着找材料，学着做鱼饵，这样才算是他自己的本领.

数学核心素养的提出，以及今年题目的变化，都在告诉我们要重视数学核心概念的本质属性，重视数学实际应用和学生的生活体验，重视数学文化.要着重培养学生阅读数学、理解数学的能力，更要培养学生提出问题，分析问题，解决问题的能力，这才是学习数学的意义所在！