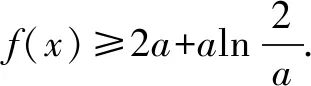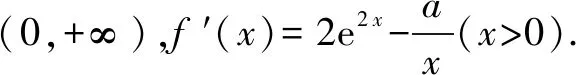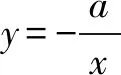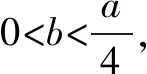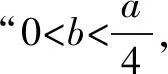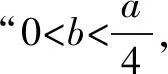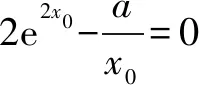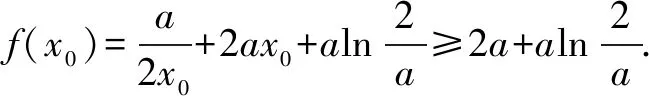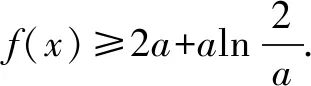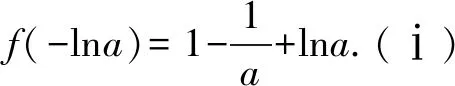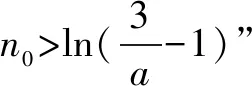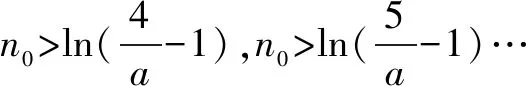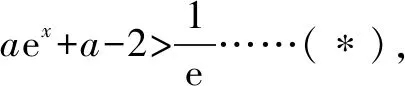“神秘”赋值的玄机

黄光鑫

(四川省四川师范大学附属中学 610066)

新课标高中数学不讲极限的内容，使得一类用导数方法讨论函数零点的题目经常采用赋值的方法说明函数值的正负，进而说明函数图象的走势，讨论函数零点的问题.有些赋值比较容易想到，有些赋值在学生看来简直是神来之笔，从天而降，无法想象！市面上不少参考书也是照搬照抄，不动脑筋！在各种不同的参考书上对同一个题目都是千篇一律的赋值方式！学生当然会问这背后的玄机在哪里？能不能想出另外的赋值方式？本文将和大家一起探讨这些“神秘”赋值的玄机，请不吝赐教.

例1 (2016·全国Ⅰ卷)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1,x2是f(x)的两个零点，证明：x1+x2<2.

解(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).①设a=0,则f(x)=(x-2)ex,f(x)只有一个零点.

②设a>0,则当x∈(-∞,1)时，f′(x)<0;当x∈(1,+∞)时，f′(x)>0.所以f(x)在(-∞,1)上单调递减，在(1，+∞)上单调递增.

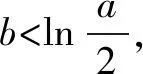
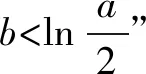
③设a<0,由f′(x)=0得x=1或x=ln(-2a).

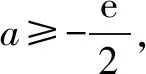
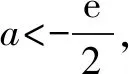
综上，a的取值范围为(0，+∞).

(2)不妨设x1f(2-x2),即f(2-x2)<0.

由于f(2-x2)=-x2e2-x2+a(x2-1)2,而f(x2)=(x2-2)ex2+a(x2-1)2=0，所以f(2-x2)=-x2e2-x2-(x2-2)ex2.

设g(x)=-xe2-x-(x-2)ex,则g′(x)=(x-1)(e2-x-ex).

所以当x>1时，g′(x)<0，而g(1)=0，故当x>1时，g(x)<0.

从而g(x2)=f(2-x2)<0,故x1+x2<2.

例2已知函数f(x)=ex+ax-a(a∈R且a≠0).

(1)若f(0)=2，求实数a的值，并求此时f(x)在[-2，1]上的最小值；

(2)若函数f(x)不存在零点，求实数a的取值范围.

解(1)由题意知，函数f(x)的定义域为R，又f(0)=1-a=2，得a=-1，所以f(x)=ex-x+1，求导得f′(x)=ex-1.

易知f(x)在[-2，0]上单调递减，在[0，1]上单调递增，所以当x=0时，f(x)在[-2，1]上取得最小值2.

(2)知f′(x)=ex+a，由于ex>0，

①当a>0时，f′(x)>0，f(x)在R上是增函数，

当x>1时，f(x)=ex+a(x-1)>0；

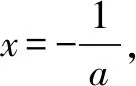
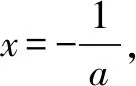
②当a<0时，令f′(x)=0，得x=ln(-a).在(-∞，ln(-a))上，f′(x)<0，f(x)单调递减;在(ln (-a)，+∞)上，f′(x)>0，f(x)单调递增.所以当x=ln(-a)时，f(x)取最小值.

函数f(x)不存在零点，等价于f(ln(-a))=eln(-a)+aln(-a)-a=-2a+aln(-a)>0，解得：-e2

综上所述，所求实数a的取值范围是(-e2，0).

例3 设函数f(x)=e2x-alnx.

(1)讨论f(x)的导函数f′(x)零点的个数；

当a≤0时，f′(x)>0，f′(x)没有零点；

所以f′(x)在(0，+∞)上单调递增.

(2)证明由(1)，可设f′(x)在(0，+∞)上的唯一零点为x0，当x∈(0，x0)时，f′(x)<0；当x∈(x0，+∞)时，f′(x)>0.

故f(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增，所以当x=x0时，f(x)取得最小值，最小值为f(x0).

例4[2017年新课标卷(Ⅰ)(21)]已知函数f(x)=ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.

解(1)f(x)的定义域为(-∞,+∞)，f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1).

①若a≤0，则f′(x)<0，所以f(x)在(-∞,+∞)单调递减；②若a>0，则由f′(x)=0得x=-lna.当x∈(-∞,-lna)时，f′(x)<0；当x∈(-lna,+∞)时，f′(x)>0所以f(x)在(-∞,-lna)单调递减，在(-lna,+∞)单调递增.

从以上几个例题可以隐隐略略看出：这类赋值问题，我们要仔细观察所出现式子的结构特征，根据问题的需要，结合一些已知的恒等式和不等式，借助于待定系数法或寻找中间变量总能找到成功赋值的方法！“神秘”赋值其实并不“神秘”！