温度作用下水泥面板的应力特征

曾惠珍

(福建船政交通职业学院道路工程系， 福州 350007)

引 言

水泥混凝土路面在我国使用时间较早，应用也很广泛。水泥混凝土路面板的使用寿命受多种因素的影响，包括施工质量、交通状况、环境条件、结构设计状况等，这些因素都会影响面板中裂缝的形成与发展。

水泥路面板内存在温度梯度时，将导致板的翘曲变形，由于自重和约束的作用板内将会产生温度应力。在以往路面板的温度应力研究中，没有考虑固化温度梯度影响下的温度应力状态。本文依据温度应力的研究现状，通过三维有限元分析软件EverFE2.24对考虑固化温度梯度的水泥混凝土路面板的温度应力及其耦合应力进行分析，得到一些规律性的认识。

1 温度应力的研究现状

1927年Westergaard[1]推导出水泥混凝土路面温度应力分析方法，并将温度应力分为由路面板整个断面内温度均与变化引起的伸缩应力和由温度沿路面板深度方向线性分布引起的翘曲应力。1938年，Bradbury[2]改进了Westergaard温度应力计算方法，得出有限尺寸板的计算温度翘曲应力的方法。到目前为止，各国仍然使用这个理论作为设计水泥混凝土路面设计的理论基础。

2009年李嘉[3]等通过应用大型有限元软件ANSYS10.0 对CRCP+AC 复合式路面在夏季高温条件下的瞬态温度场进行了模拟，利用温度结构耦合原理计算了路面结构在日周期气温下的温度应力。

2009年郑秉乾[4]通过建立轴载和负温度梯度耦合作用下的有限元计算模型，对不同轴型和不同板尺寸下的力学响应进行分析计算。

2014 年田波[5]实测了水泥混凝土路面板在不同基层类型上的内响应，分析了基层类型差异引起板内应力的变化规律。

2015年颜可珍等[6]根据实测温度非线性分布数据，研究了温度对混凝土路面板应力和变形的影响，提出负温度梯度下板顶最大应力计算公式。

2015年魏亚等[7]通过对西南农村地区路面板内温度进行实际测量，研究了温度梯度和交通荷载的不利组合对不同尺寸路面板的应力影响。

2019年朱华胜等[8]人利用ANSYS有限元软件对道路硅酸盐水泥混凝土面板进行翘曲量研究，得到增加基层厚度和模量可以减小温度作用引起板的翘曲量。

2019年姜利等[9]人采用三维有限元模型分析，发现应力吸收层在低温条件下，随着降温幅度的增加应力集中现象越明显；模量增加，层底温度应力增大。

国内外的研究表明，决定混凝土板厚度或者促使板产生疲劳断裂的主要因素是温度应力和荷载应力的共同作用。目前，在水泥混凝土路面温度翘曲的试验研究中，针对路面板的温度应力单独作用下的关系还缺乏系统和有效的研究。

本文将测得的温度采用三维有限元分析软件EverFE2.24，计算温度场的温度应力，研究路面板厚度变化、面板尺寸变化、面层与基层接触面的变化对温度应力的影响，以及不同施工时段对其温度与荷载的耦合应力的影响，为水泥混凝土路面结构温度应力的研究提供了参考。

2 有限元模型及参数

EevrFE有限元程序是专门用于模拟带接缝的水泥混凝土路面(JPCP)在轮载及温度作用下的力学响应的一款三维有限元分析软件。

如图1所示，EverFE2.24采用5种离散单元来模拟各结构层：20节点的二阶立方体单元用来离散面板、弹性基层和底基层；8节点平面二阶单元用来模拟液体地基；16节点二阶接触面单元用来模拟骨料嵌锁剪力的传递以及路面板与基层接触界面。

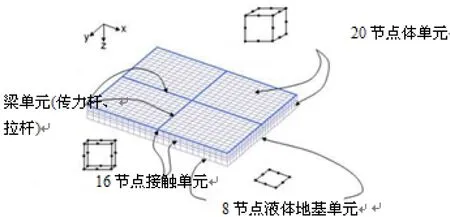
图1 单元划分及类型

2001年Rasmussen和Rozychi[10]给出了这种弹塑性剪力传递模型的本构关系。它用滑动位移δ(mm)和初始分布刚度KSB(MPa/mm)来表征，并通过试验得到了不同种类基层与路面板接触界面参数，见表1。当KSB很小时，相当于在接触界面处没有摩擦力；当KSB值很大时，这种模型类似于有较大摩擦系数的库仑摩擦模型。没有特殊说明时，本文采用水泥稳定碎石基层，接触面参数参照表格取值。

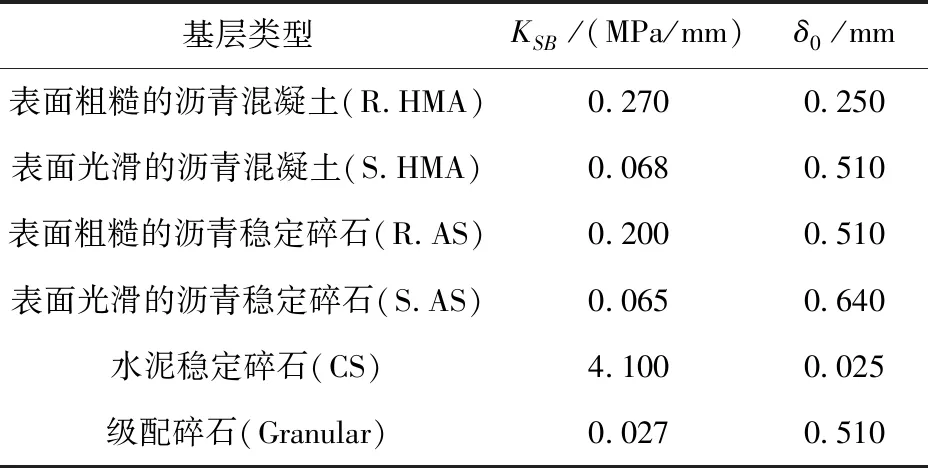
表1 典型基层与路面板接触界面参数

3 计算参数取值

3.1 温度梯度取值方法

国外研究表明[11-12]路面服务阶段的长期使用性能受到水泥路面刚刚铺筑完的3天的早期性状的影响，这些早期性状包含有接缝张开量、固化翘曲、收缩开裂等。

研究发现[13-14]夏季白天施工时，水泥混凝土路面由于当时的气温和太阳辐射较高，使其板顶温度比板底高，水泥混凝土在这一温度梯度下凝固而记忆了一个凝固温度，因此平整的水泥混凝土面板并没有对应零温度梯度，而往往对应一个正的温度梯度，此后在实际的零温度梯度下，板会自然向上翘曲，这样一个有影响的正温度梯度就固化到板中。固化温度梯度受水泥混凝土路面板的浇筑时间、凝固时间、养护时的天气和混凝土温度的显著影响。

基于固化温度梯度的概念，在水泥混凝土路面板温度应力计算过程中，水泥混凝土面板的计算温度应从实际路面温度中扣除路面板终凝时刻的固化温度梯度。其中，扣除的固化温度梯度包含板顶底固化温度梯度差以及板底终凝时刻对应板底基础温度。

因此，本文计算模型为：路面的实测温度梯度-路面凝固的温度梯度=计算时采用的温度梯度，如图2所示。

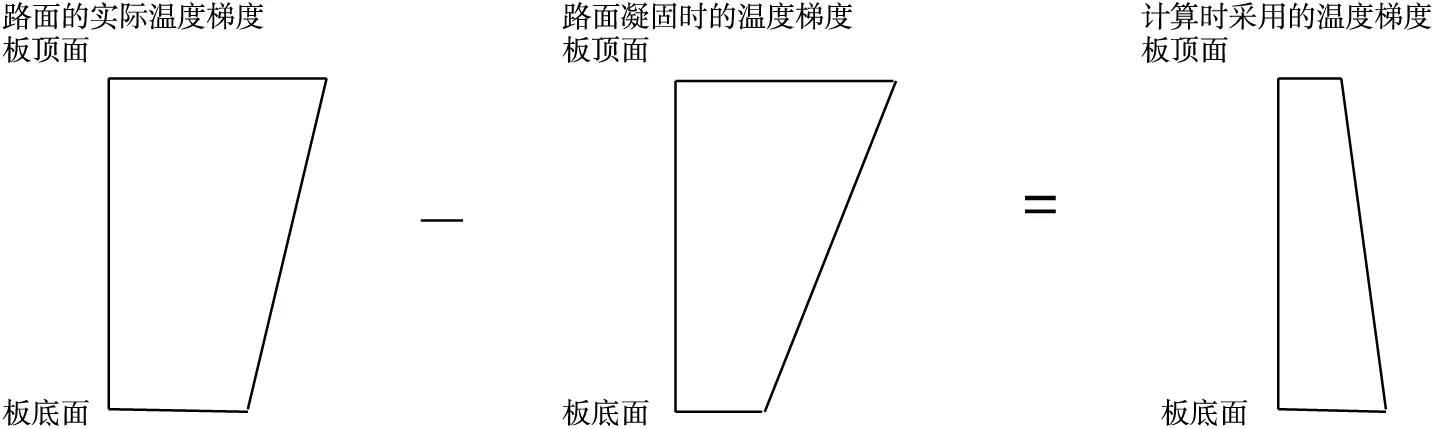
图2 温度梯度值取值方法

其中，实际最大正温度梯度取自2007.4.21中午13∶00点的福州316国道，其板底温度为23.34 ℃；板顶温度为50.2 ℃。凝固温度梯度以2007.6.25晚上19∶00点施工的福州马尾路段温度为依据，取10个小时后的凝固温度板底温度为38.25 ℃，板顶为35.32 ℃。

图3为水泥混凝土路面晚上施工时线性温度梯度的取值计算，表示了计算时所采用的温度梯度值的取值过程。

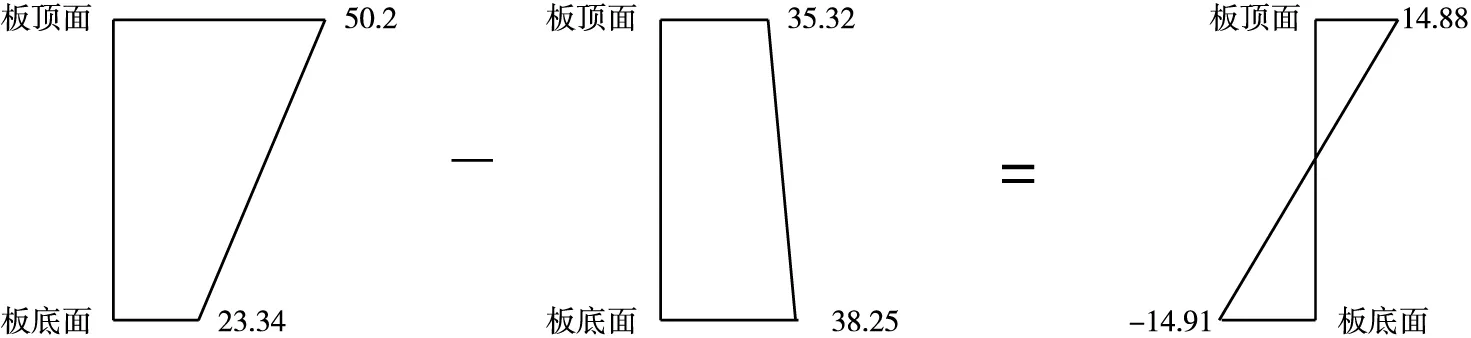
图3 当晚上施工时，温度沿板厚呈线性变化，最大正温度梯度

本文暂不考虑徐变、干缩、湿度梯度对使用阶段路面的影响，重点讨论固有温度梯度与使用阶段路面的温度梯度耦合作用下的路面性状。

3.2 计算参数取值

本文所采用的计算参数：面板尺寸取4.5 m×5 m，板厚取240 mm，模量取30 GPa，基层厚取150 mm，模量取5000 MPa；板与地基的层间接触面取为水泥稳定碎石(δ0=0.025，KSB=4.1)。图4为10 t单轴-双轮荷载分别作用在纵缝边缘中部和离板角40 cm的横缝位置。取晚上施工时段的凝固温度作为预应变时的温度，为了精确计算，将面板沿深度变化的温度梯度取为非线性，如图5所示。

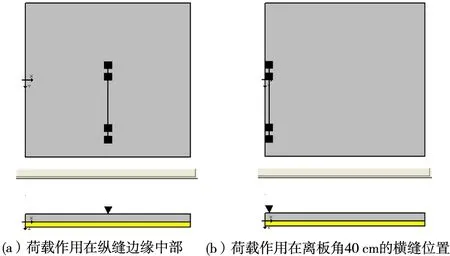
图4 面板尺寸和荷载位置

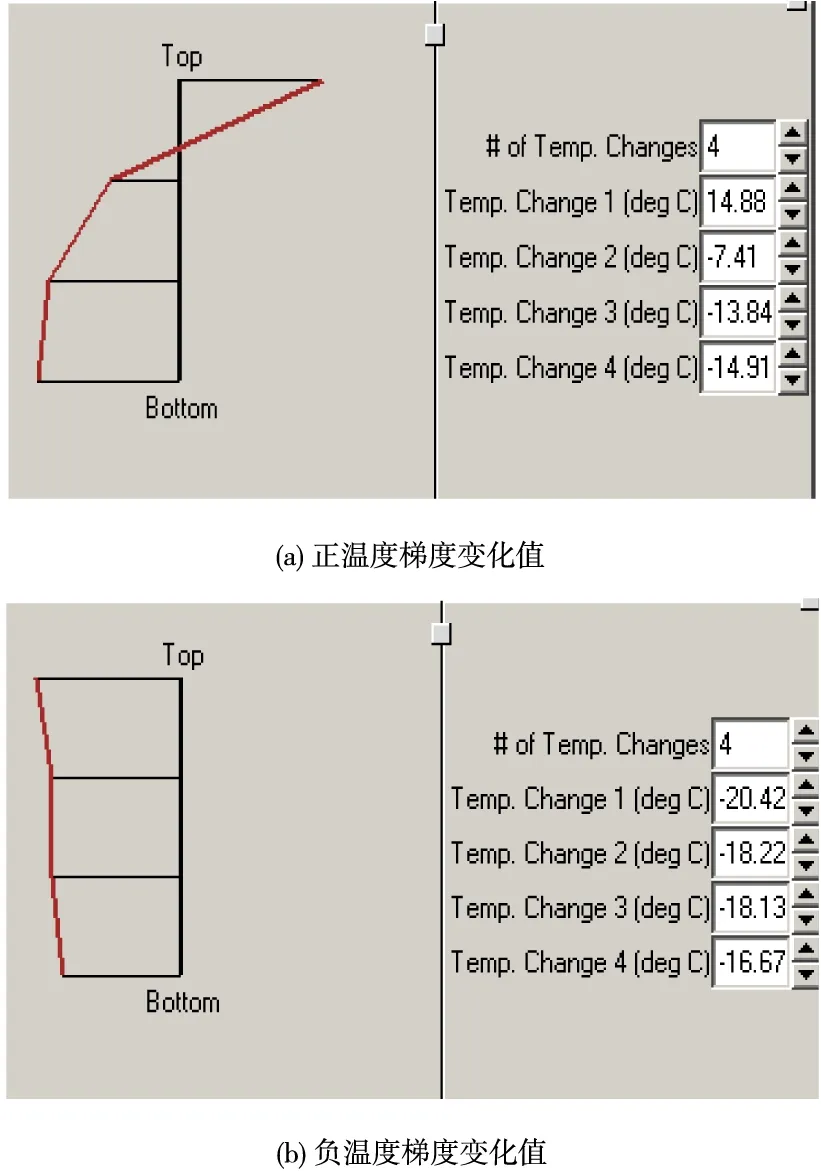
图5 温度梯度沿板厚呈非线性分布

4 水泥混凝土路面温度应力影响因素分析

4.1 温度沿板厚呈线性考虑与非线性考虑的对比分析

通过采用EverFE2.24计算软件，分别考虑温度沿板厚呈线性及非线性分布时，对温度应力进行对比分析，结果见表2。

表2 线性与非线性最大温度应力值(单位：MPa)

对比在没有荷载作用下温度应力分析，4.5 m×5 m面板温度梯度非线性分布比温度梯度线性分布的最大温度应力大10.9%，3.75 m×5 m面板非线性时比线性时大4.88%，4.5 m×4.5 m面板非线性时比线性时大32.88%，5.5 m×5 m面板线性比非线性时大10.2%。因此，可知长宽比越小则线性与非线性计算出的最大温度应力误差越大，反之长宽比越大线性与非线性计算出的温度应力误差越小；当面板宽度小于长度时线性的最大温度应力比非线性小，当面板宽度大于长度时，线性的最大温度应力比非线性大。以4.5 m×5 m面板为例，面板在正、负温度梯度下板的变形如图6所示，图6(a)为面板在正温度梯度下呈向上突起；图6(b)为面板在负温度梯度下向上凹起。

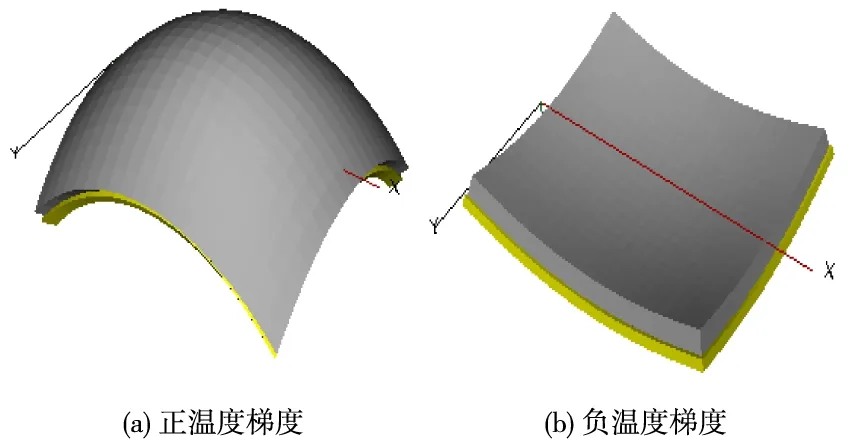
图6 面板在正、负温度梯度下的变形图

如图7所示，为标准面板在正温度梯度下出现最大拉应力值那一层面的应力分布图。图7可见，当温度梯度线性分布时，温度应力最大值出现在板底纵缝中部；当温度梯度呈非线性分布时，温度应力最大值出现在板厚中部角隅处。考虑到温度呈非线性分布时比较切合实际温度分布情况，因此，以下在讨论温度梯度沿深度分布时均考虑温度沿深度呈非线性分布。

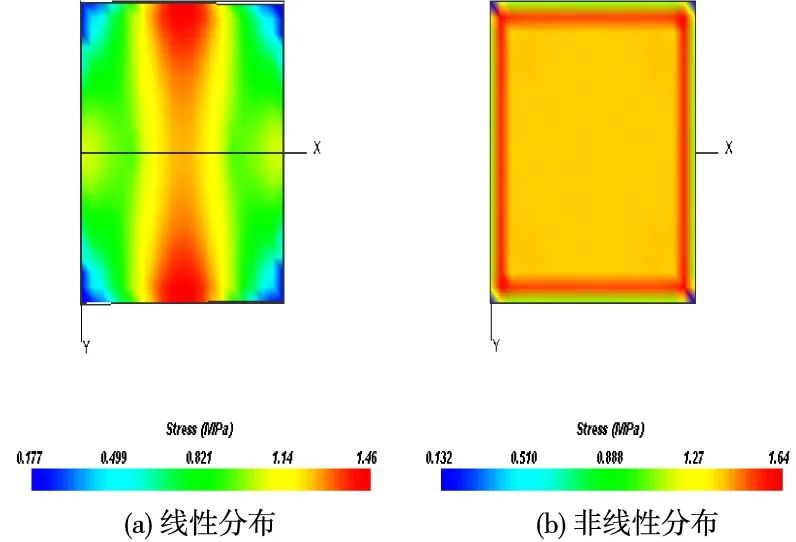
图7 最大正温度梯度下，温度梯度呈线性以及非线性分布时最大拉应力分布图

4.2 板厚变化对温度应力的影响

图8为只有温度作用下面板最大拉应力随板厚的变化情况。

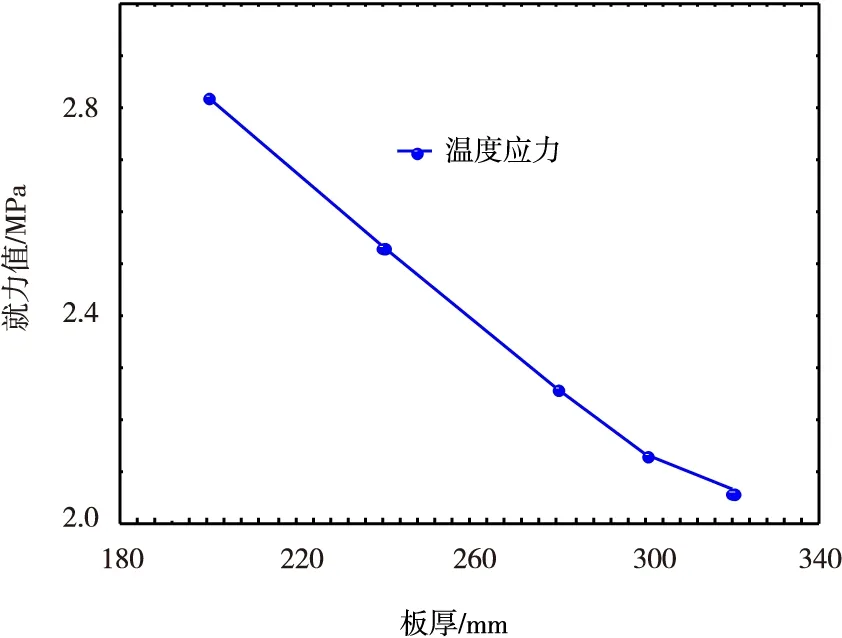
图8 面板厚度对面板最大拉应力的影响

从图8可知，随着板厚的增加，温度应力逐渐减小，其减小的幅度随着板厚的增加而减小。

4.3 面板尺寸变化对温度应力的影响

针对福建省典型路面结构，对4种不同板尺寸路面结构进行研究：4.5 m×5 m，3.75 m×5 m，4.5 m×4.5 m，5.5 m×5 m。图9和图10为南平夏季路面温度较高的一天(7月13日)的温度应力变化曲线。

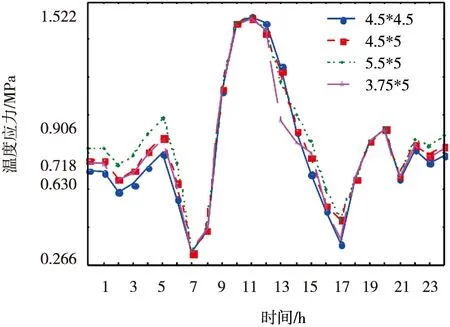
图9 不同板尺寸的温度应力值

从图9中可以看出，路面结构温度随气温和辐射的昼夜变化呈周期性变化，正温度应力在一天当中的变化情况呈半正弦波，这与实际路面结构温度场分布情况相似。1点到7点期间温度应力大致下降，但变化幅度不大，7点时最大温度应力为0.266 MPa，7点之后，随着气温的升高温度应力逐渐加大，变化幅度也逐渐加大，到中午11～12点期间温度应力达到最大值，最大可达1.522 MPa，而后逐渐下降，到17点时最大温度应力为0.314 MPa，17点过后温度应力又逐步上升。

结合整体一天变化情况，不同板尺寸对温度应力产生的影响幅度不大，当板尺寸取为5.5 m×5 m时，板受到最不利的温度应力值，当板尺寸为4.5 m×4.5 m时，面板受到的温度应力值最小。

图10可以看出，最大正温度应力与最大负温度应力达到峰值的时间基本一致，在中午11～12点期间达到，可见要讨论温度应力最不利值应该选择在中午12点左右。并且最大负温度应力比最大正温度应力要大3倍，因此在考虑面板的温度应力时，负温度应力不容忽视。

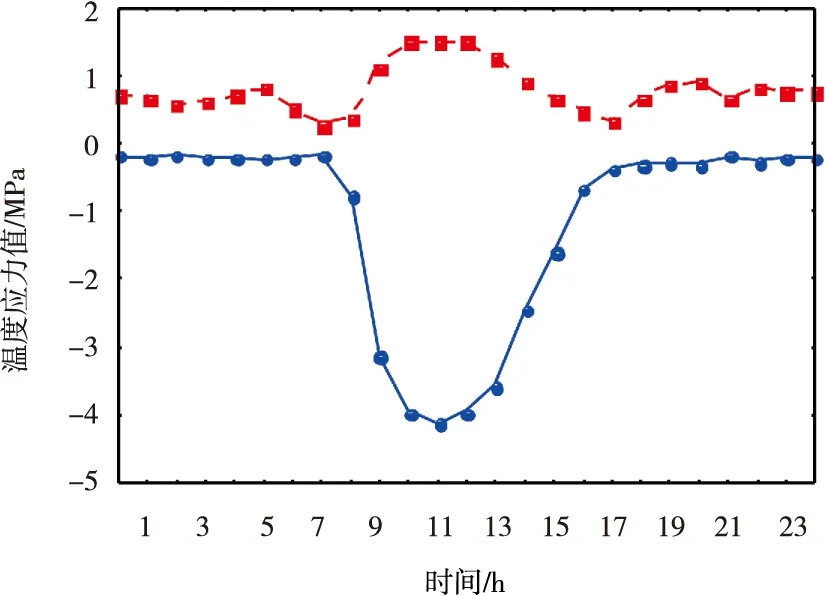
图10 4.5 m×4.5 m板正负温度应力变化情况

4.4 面板与基层接触面变化对温度应力的影响

当面板与基层接触面不同时，其对温度应力会产生不同的影响。根据计算模型，选取8种层间接触面进行对比研究，计算结果如图11所示。

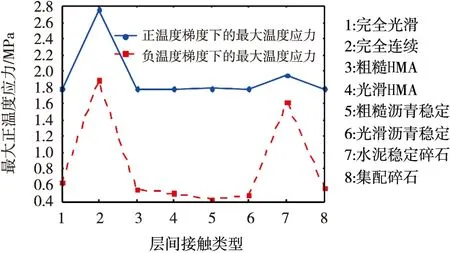
图11 层间接触面不同时的温度应力值

图11可见，当层间接触条件为完全光滑的时候，计算所得面板所受的温度应力值偏小。而当层间接触条件为完全连续时，计算所得面板所受的温度应力值为最大。在正温度梯度作用下，面板所受温度应力值大小依次为：完全连续>水泥稳定碎石>粗糙沥青稳定>粗糙HMA>光滑HMA=光滑沥青稳定=集料=完全光滑。可见，接触面为水泥稳定碎石时的温度应力值相对其它接触面来说，更接近于完全连续。规范为计算方便，将水泥稳定碎石的层间接触条件用完全连续来代替，但从图11中可见，层间接触区完全连续，其计算的温度应力结果偏大，过于保守。

5 不同施工时段时耦合应力分析

水泥混凝土路面在白天施工以及晚上施工时，由于不同时段施工，则混凝土凝固的时间是不同的，白天施工由于受到太阳照射和辐射的影响，凝固时间相对比较短，并且凝固时的温度比较高；而当晚上施工时则凝固时间相对比较长，且凝固时的温度比较低。

对马尾实测数据对白天7∶00和晚上19∶00两个时间段下铺筑的路面，面板在后期使用阶段受到最大正、负温度梯度时，荷载和温度产生的耦合应力值进行对比分析，得到不同的最大拉应力值见表3。

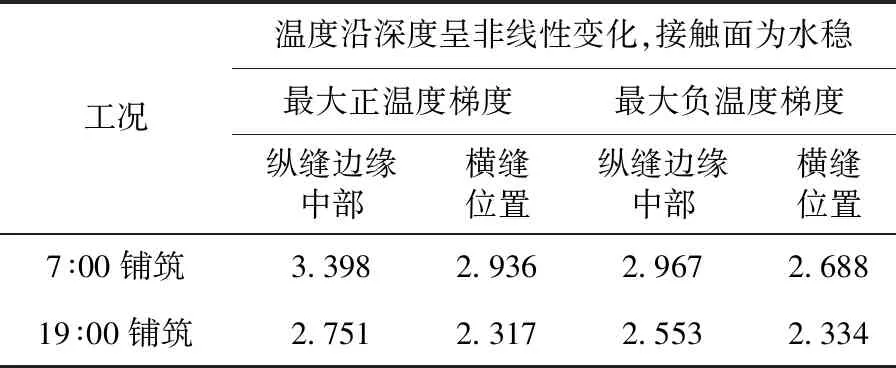
表3 荷载和温度耦合应力值(单位：MPa)

注：纵缝边缘中部、横缝位置分别指荷载位置在离板边40 cm的纵缝边缘中部、荷载位置在离板角40 cm的横缝位置。

从表3可知，整体面板在7∶00铺筑时将比19∶00施工铺筑时产生更大的耦合应力值。当路面处于最大正温度梯度时，荷载作用在纵缝边缘中部时，7∶00施工要比19∶00施工产生的应力高19.04%，而荷载作用在离板角40 cm的横缝位置时则高21.08%左右；当路面处于最大负温度梯度时，荷载作用在纵缝边缘中部时，7∶00施工要比19∶00施工产生的应力高13.95%左右，而荷载作用在离板角40 cm的横缝位置时则高13.17%左右。可见，最大正温度梯度产生的耦合应力值要比最大负温度梯度时大，为减小面板的耦合应力值，路面板的铺筑时段最好选择在晚上。

水泥混凝土路面的长期性能与其早期施工阶段路面的性能是分不开的，而水泥混凝土路面的早期性能显著的受到外界温度场的影响，在一定的温度场的影响下，路面可能由于过大的早期温度应力而开裂，而且在早期温度场下水泥混凝土路面形成的早期固有路面形状和内在属性(路面混凝土的早期性能)，会对后期路面的长期使用性能有显著的影响。

6 结 论

采用三维有限元分析软件EverFE2.24对水泥混凝土路面结构温度应力及其耦合应力进行分析，得到一些规律性的认识：

(1) 分析了温度梯度沿板厚呈线性与非线性分布时，可知长宽比越小则线性与非线性计算出的最大温度应力误差越大，反之长宽比越大线性与非线性计算出的温度应力误差越小；当面板宽度小于长度时线性的最大温度应力比非线性小，当面板宽度大于长度时，线性的最大温度应力比非线性大。温度呈非线性分布时比较切合实际温度分布情况。

(2) 分析了板厚变化对温度应力的影响，得到温度应力沿板厚的变化先是随着板厚的增加逐渐减小，其减小的幅度随着板厚的增加而减小。计算在温度梯度沿板厚非线性变化时的温度应力，得到采用面板尺寸为5.5 m×5 m时，会产生最大的温度应力值，面板尺寸为4.5 m×4.5 m能较好改善纵缝边缘中部的应力值。本文研究的不同面板尺寸还不够全，需进一步研究更多不同尺寸与结构组合的非线性温度应力变化规律。

(3) 分析了面板与基层接触面变化对温度应力的影响，得出层间接触区完全连续，其计算的温度应力结果偏大，过于保守。

(4) 研究了不同施工时段对其耦合应力的影响，最大正温度梯度产生的耦合应力值要比最大负温度梯度时大，为减小面板的耦合应力值，路面板的铺筑时段最好选择在晚上。