一类随机SIRS流行病模型的动力学分析
张太雷,李志民,方舒
(长安大学 理学院,陕西 西安 710064)
0 引言

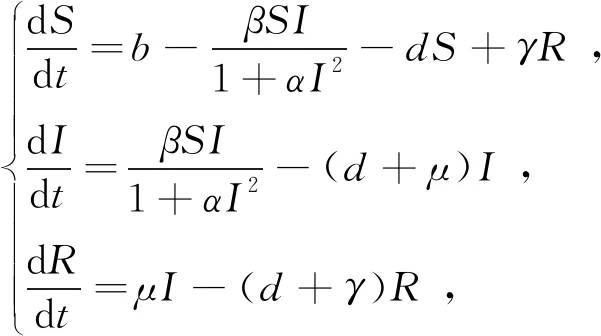
(1)
其中,S(t),I(t),R(t)分别表示t时刻的易感者、染病者和恢复者的数量。b表示对种群的常数输入率;d表示种群的自然死亡率;β表示传染率;α表示人们心理作用或外界采取相应的措施所产生的抑制效应;γ表示恢复者丧失免疫率,γ>0意味着恢复者具有暂时免疫力,γ=0意味着恢复者具有永久免疫力;μ表示染病者的恢复率。这里所有的参数均为正常数。
其中
由系统(1)的各式相加得
b-d(S(t)+I(t)+R(t)),
因此有
S(t)+I(t)+R(t)=
即有
因此,系统(1)的正向不变集是
现实世界的生物生长会受到各种随机因素的干扰,因此,随机数学模型[6-17]的研究和确定性数学模型的研究相辅相成,使得人们对生物在发展过程中行为的了解和认识更全面、更深刻。特别地,在文献[9]中,周艳丽等人考虑了模型(1)中感染率的参数扰动,研究了如下随机模型:
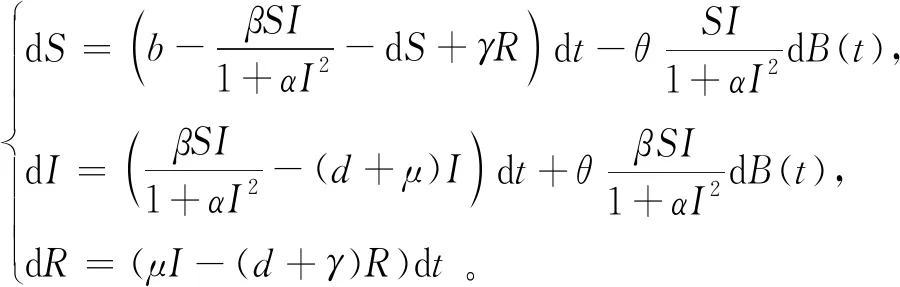
(2)
在文献[14]中,刘群等人研究了一类随机SIRI流行病模型, 并且在模型建立中考虑不同于模型(2)的参数扰动型随机模型。受上述文献中关于随机模型的研究和文献[14]的建模启发,本文在确定性模型(1)的基础上建立如下随机SIRS流行病模型:
(3)
其中B1(t),B2(t),B3(t)是独立的布朗运动,σ1,σ2,σ3为其强度系数。从模型(1),(2),(3)可以看出,确定性模型(1)的无病平衡点和地方病平衡点不是随机模型(3)的无病平衡点和地方病平衡点。
1 全局唯一正解
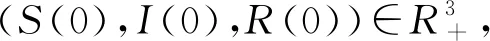



考虑如下Lyapunov函数
V(S(t),I(t),R(t))=(S-1-lnS)+
(I-1-lnI)+(R-1-lnR)
(4)
易证对于任意u>0,有u-1-lnu≥0成立,故有V(t)正定。由伊藤公式[10]计算可得
dV=LVdt+σ1(S-1)dB1(t)+
σ2(I-1)dB2(t)+σ3(R-1)dB3(t)
(5)
其中

(6)
考虑函数

(7)
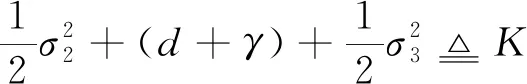
(8)
所以
dV≤Kdt+σ1(S-1)dB1(t)+
σ2(I-1)dB2(t)+σ3(R-1)dB3(t)
(9)
现将(9)两端从0到τk∧T积分并取期望可得:
E[V(S(τk∧T),I(τk∧T),R(τk∧T))]≤
V(S(0),I(0),R(0))+KT
(10)

V(S(τk),I(τk),R(τk))≥
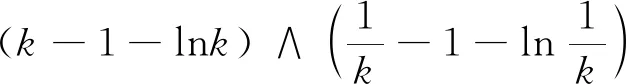
(11)
所以
V(S(0),I(0),R(0))+KT≥
E[IΩkV(S(τk,ω),I(τk,ω),R(τk,ω))]≥
(12)
其中IΩk表示Ωk的示性函数。当k→∞,则有
∞>V(S(0),I(0),R(0))+KT=∞,
(13)
与假设矛盾,所以必有τ∞=∞a.s.,这说明(S(t),I(t),R(t))以概率1在有限时间内不会产生爆破。证明完毕。
2 随机模型(3)的解在确定性模型(1)的无病平衡点附近的波动情况
定理2 当R0≤1,且满足
其中
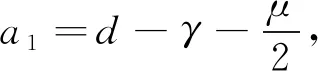
证明定义Lyapunov函数
V=V1+V2+V3+V4
(14)
其中V1,V2,V3,V4分别为
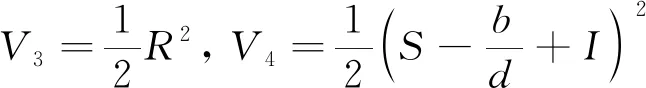
(15)
利用伊藤公式计算得
dV1=LV1dt+W1dB1,
dV2=LV2dt+W2dB2,
dV3=LV3dt+W3dB3,
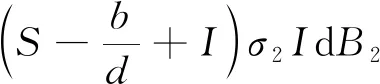
(16)
其中
W2=σ2I2,
W3=σ3R2,

(17)
进一步计算可得

(18)
由(14)-(18)式整理可得
(19)
进一步得到
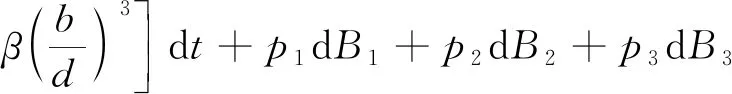
(20)
对(20)两端分别从0到t积分,并取期望得到
EV(t)-EV(0)≤
E(p1M1+p2M2+p3M3)
(21)
其中
则Mi(t)是连续局部鞅,且满足
Mi(0)=0,
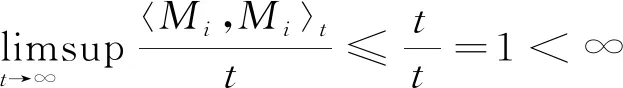
(22)
根据鞅的强大数定律[13]可得
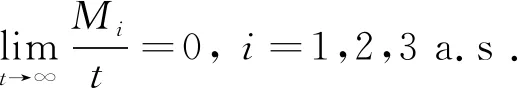
(23)
因此

(24)
证明完毕。
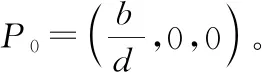
3 随机模型(3)的解在确定性模型(1)的地方病平衡点附近波动情况
定理3 当R0>1,且满足
其中,
证明当R0>1时,确定性模型(1)存在唯一的地方病平衡点P*=(S*,I*,R*),且满足
μI*-(d+γ)R*=0
(25)
定义Lyapunov函数
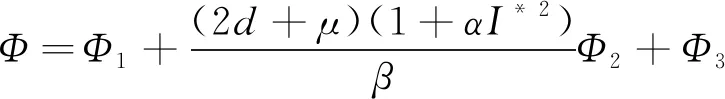
(26)
其中Φ1,Φ2,Φ3分别为

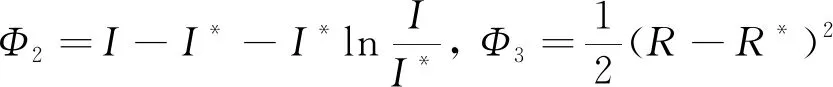
(27)
利用伊藤公式计算得
-d(S-S*)2-(d+μ)(I-I*)2-(d+μ)(S-S*)(I-I*)-d(S-S*)(I-I*)+
-d(S-S*)2-(d+μ)(I-I*)2-(2d+μ)(S-S*)(I-I*)+
(28)
考虑到
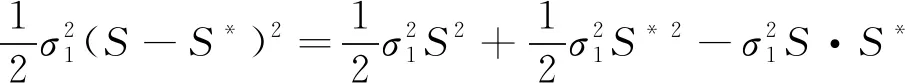
(29)
即有

(30)
同理有

(31)
另外由2ab≤a2+b2可得
2(R-R*)(I-I*)≤
(R-R*)2+(I-I*)2, 2(R-R*)(S-S*)≤
(R-R*)2+(S-S*)2
(32)
由(26)-(32)式整理得到
LΦ≤-d(S-S*)2-(d+μ)(I-I*)2-
(2d+μ)(S-S*)(I-I*)+
γ(S-S*)(R-R*)+γ(I-I*)(R-R*)+
(d+γ)(R-R*)2+μ(R-R*)(I-I*)+
(33)
进一步得到
dΦ≤LΦdt+WdB(t)
(34)
其中
WdB(t)=σ1S(S-S*+I-I*)dB1+
σ2I(S-S*+I-I*)dB2+
(R-R*)2σ3RdB3≤
σ1S(S-S*+I-I*)dB1+(R-R*)2σ3RdB3≤
q1dB1+q2dB2+q3dB3
(35)
对(34)两端分别从0到t积分,并取期望得到
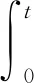
b2(I(r)-I*)2-b3(R(r)-R*)2]dr+
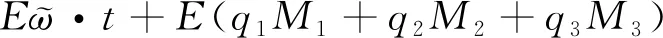
(36)
其中
则Mi(t)是连续局部鞅,且满足
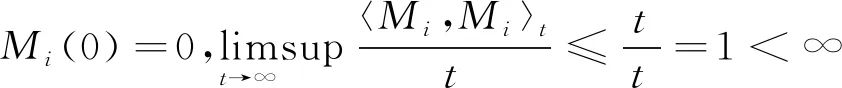
(37)
根据鞅的强大数定律可得

(38)
因此

(39)
证明完毕。
4 随机持久性
下面讨论随机系统(3)平均持续存在,关于随机持久性的定义见文献[18]。

证明由定理3,可得

(40)
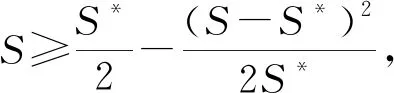
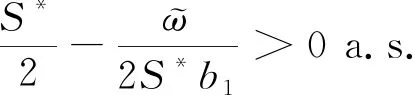
(41)
同理有

(42)
定理证毕。
5 随机灭绝性
本节指出当外界环境干扰强度较大时能导致疾病灭绝,即大噪声能导致疾病消失。
引理1[15]设随机模型(3)的解(S(t),I(t),R
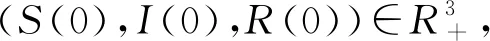
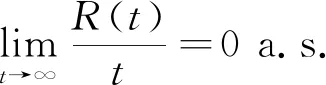
(43)

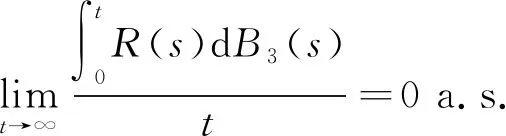
(44)
定义
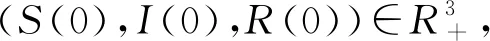
和
证明令Q(t)=μI(t)+(μ+d)R(t),利用伊藤公式计算得
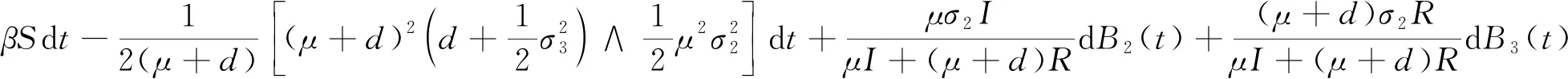
(45)
由随机模型(3)可知
d(S(t)+I(t)+R(t))=
[b-d(S(t)+I(t)+R(t))]dt+
σ1S(t)dB1(t)+σ2I(t)dB2(t)+σ3R(t)dB3(t)
(46)
对(46)从0到t积分,再由引理1中(43)和(44)得到
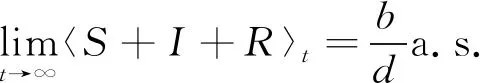
(47)
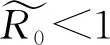
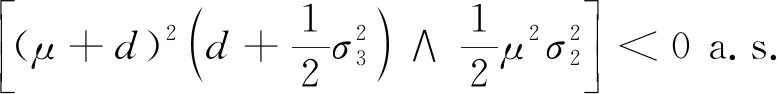
(48)
即推出
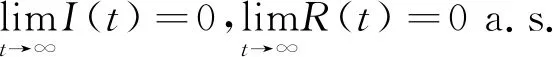
(49)
另一方面,由(46)得到
b-d〈S〉t-d〈I〉t-d〈R〉t+
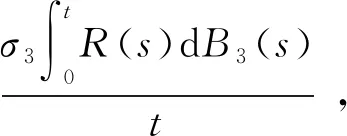
(50)
由引理1中(43)、(44)和(49),得到
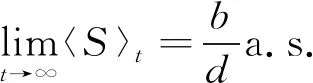
(51)
定理证毕。
6 结论

对于确定性模型和对应的随机模型而言,随机模型更加符合客观实际情况,更有助于了解流行病的传播机理。另一方面,由于流行病在现实环境中的传播过程非常复杂,会受到许多因素影响,所以下一步研究工作是构建其他形式的随机流行病模型,并研究其动力学行为。

