分段线性模型误差分布差异的经验似然比检验
高鹏丽,夏志明
(西北大学 数学学院,陕西 西安 710127)
0 引言
经验似然最早是由Owen[1]提出的,这一方法与经典的统计方法相比较有很多突出的优点。因此,这一方法被统计学家们应用到各种统计模型及各种领域。如Owen[2]和Chen[3]将其应用到线性回归模型的统计推断;Zhu和Xue[4]发展了部分线性模型的经验似然;Liu[5]等应用经验似然方法研究了两个维样本的不同均值的结构置信域。Zou[6]等基于经验似然应用非参数方法检测来自独立随机变量序列的变点。Einmahl和McKeague[7]基于残差利用经验似然检验一组独立的时间序列中是否至多只有一个变点。近来,Kitamura[8]等将经验似然应用到经济模型的研究中;Zou[9]等将经验似然方法应用到了多元变点问题中。但是至今没有人研究过将经验似然应用于由于误差发生变化的分段线性模型中。

1 统计模型
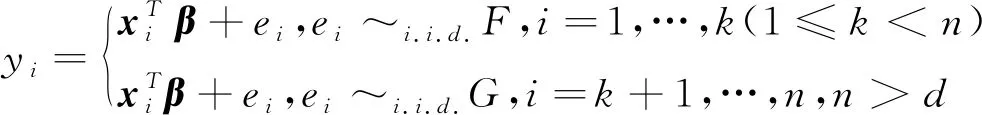
(1)
这里xi∈Rd,i=1,…,n是非随机的,β∈Rd是未知系数向量,{ei}是独立随机误差序列,满足Eei=0,k的位置已知,分布函数F和G未知。模型(1)可写成如下矩阵形式
Y=Xβ+e,
其中
X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T,
β=(β1,β2,…,βd)T,
e=(e1,e2,…,ek,ek+1,…,en)T。
为了证明后面的定理,先给出如下假设和引理。
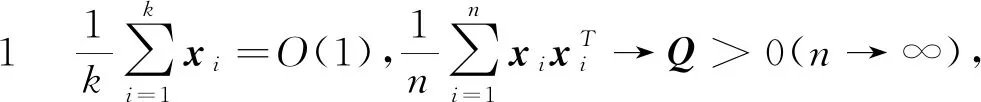


假设4当n→∞,有k→∞,n-k→∞。
引理1 对k→∞,有:

证明因为
由假设1-2,有
更进一步
本文的目的是构造一个检验方法,基于模型(1)检验分段线性模型中两组误差之间是否存在差异,于是考虑如下假设检验问题
H0:F(t)=G(t)↔H1:F(t)≠G(t),t∈(-∞,∞)。
2 分段线性模型中残差的经验分布及其性质
为了得到残差,我们首先给出回归系数β的最小二乘估计如下:

定理1对模型(1),如果假设1-4成立,当n→∞时,在H0成立的条件下有下面结论成立。


证明不失一般性,我们只证明结论(i).根据定义,有

因此可以得到
由假设1-4和引理1,有
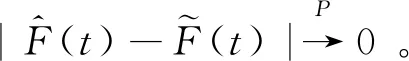
同理,结论(ii)也成立。
定理2对模型(1),在假设1-4下,当H0成立时,有


证明由Glivenko-Cantelli定理有

再结合定理1,知定理2的结论显然成立。
3 分段线性模型中残差的经验似然比检验
本文考虑误差来自两个独立总体的检验问题,求得到经验似然比统计量值后,为根据检验水平去决定临界值,需要求出统计量在原假设成立时的分布。但在一般情况下,很难得到统计量的精确分布,此时可以求出它的渐近分布近似的决定临界值。
3.1 基于误差构造经验似然比函数

类似的,在H0下的非参数最大似然函数为
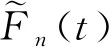
定义局部经验似然比为
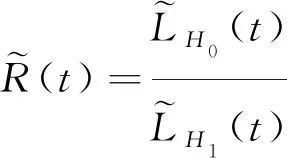
(2)
给(2)式两边同时取对数就可以得到对数局部经验似然比为
则经验似然比函数为
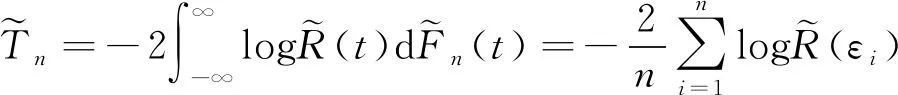
(3)

定理3 在H0成立的条件下, 当假设1-4成立时,有
其中B是一个标准的布朗桥。


(4)
和

(5)
在δ上一致成立。下面我们首先证(4)式。由于δ≤y≤1-δ,通过泰勒展开,有
考虑(4)式就相当于考虑
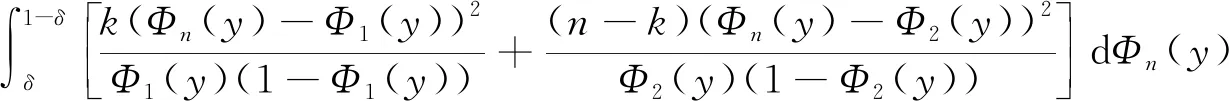
(6)


(7)

引理3[12-15]在引理2的条件下, 存在一个标准的布朗桥序列{Bn}满足
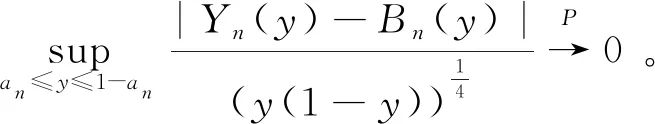
只考虑求和的第一项, 第二项很容易处理。由引理2可知第一项以很高的概率在区域上一致有上界

由引理3,有
3.2 基于残差构造经验似然比检验统计量
基于残差序列,类似的定义

相应的局部经验似然比定义为
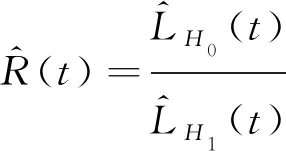
(8)
给(8)式两边同时取对数得到对数局部经验似然比为
因此经验似然比检验统计量为
定理4 在H0成立的条件下,当假设1-4成立时,有
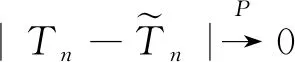
(9)
证明证明(9)等价于证明

由于

先考虑求和的第一项, 第一项可以化简为

(10)
由定理1以及随机变量的连续函数的收敛性可知(10)式依概率收敛于0,同理可证求和的第二、三、四项均依概率收敛于0。因此有
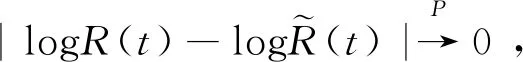
即

定理5在H0成立的条件下,当假设1-4成立时,有
证明由定理3、定理4以及Slutsky定理知
4 Monte Carlo模拟


表1 统计量经验分布各分位数、均值、方差对应值

表2 统计量渐近分布各分位数、均值、方差对应值

用R语言计算得到
D=0.036,P=0.149 7,

5 结论
本文通过经验似然的方法基于残差分析了分段线性模型中两组误差的对比检验。在原假设下成立的条件下,构造了经验似然比统计量,并求出了统计量依分布收敛的渐近分布。但是未能给出其收敛速度,这有待后边更进一步研究。文章最后进行Monte Carlo 模拟,验证理论的正确性。结果表明对于分布相同的两组误差,当样本量较大时,统计量的经验分布与渐近分布拟合较好。

