素代数上完全保k-交换性的映射

张婷,齐霄霏

(山西大学 数学科学学院,山西 太原 030006)

0 引言

令A是实或复数域F上的代数,Φ:A→A是一个映射。对每个正整数n,记Mn(A)={(Sij)n×n:Sij∈A}为A上的n阶矩阵环。于是Φ可以自然地延拓为从Mn(A)到其自身的一个映射Φn,其定义为

Φn((Sij)n×n)=(Φ(Sij))n×n。

令(P)是算子具有的某个性质,如果Φn保持性质(P),则称Φ是n-保持性质(P)的;如果对每个正整数n,Φ都是n-保持性质(P)的,则称Φ是完全保持性质(P)的。完全保持问题主要研究的是算子代数上完全保持性质(P)的映射的结构性质。

算子代数和算子空间上的完全保持问题得到了很多学者的广泛关注。假设B(X)是Banach空间X上的有界线性算子全体构成的代数。Hadwin和Larson在文献[1]中给出了B(H)(H为可分的Hilbert空间)上完全秩不增线性映射的具体刻画。之后文献[2]将[1]中的工作推广到B(X)上,并在此基础上给出了B(X)上初等算子的刻画(X为实或复Banach空间)。文献[3]和[4]则分别给出有限von Neumann代数上完全保迹秩的线性映射和一般映射的具体刻画。Banach空间标准算子代数上完全保可逆性、谱、幂等性、平方幂零性、Jordan零积、不动点和算子的核的一般满射的刻画,可分别参见文献[5-8]。最近,文献[9]将文献[8]的工作推广到了一般的环上。令A,B分别是无限维实或复Banach空间X,Y上的标准算子代数,文献[7]证明了从A到B的每个完全保交换性的满射都是同构的非零常数倍或是共轭同构的非零常数倍。之后,文献[10]将[7]的工作推广到了含单位元的素环R上,证明了从R到其自身的每个完全保交换性的满射Φ都具有形式Φ=Φ(I)Ψ,其中Φ(I)是环R中心中的可逆元,Ψ是R上的环同构。

对任意正整数k,A,B∈A的k-交换子定义为[A,B]k=[[A,B]k-1,B],其中 [A,B]0=A,[A,B]1=[A,B]=AB-BA(参见文献[11-12])。k-交换子的概念出现在著名的Baker-Compbell-Hausdorff公式

中,它在量子力学中经常被用到。对于映射Φ,对任意A,B∈A,若当[A,B]k=0时有[Φ(A),Φ(B)]k=0成立,则称Φ保k-交换性;若[A,B]k=0当且仅当[Φ(A),Φ(B)]k=0成立,则称Φ双边保k-交换性。

受上述文献的启发,本文的主要目的是以k-交换性为不变量,继续来研究素代数上的完全保持问题。

令R是环,Z(R)⊆R表示R的中心。对任意X,Y∈R,若XRY={0}蕴涵X=0或者Y=0,则称R是素环。Q=Qmr(R)表示R的极大右商环。Q的中心C称为R的扩展中心。如果R是素环,那么C是一个域。对更多关于素环的性质,可参见文献[13]。

令A是实或复数域上的含单位元I的素代数,k>1是一个整数。第一节给出了本文的主要结果,证明了A上完全保k-交换性的满射Φ具有形式Φ=Φ(I)Ψ,其中Φ(I)∈Z(A)是可逆元,Ψ:A→A是环同构(定理1)。第二节给出了第一节中主要结果的一些应用。具体地,主要结果应用于算子代数上,分别得到了因子von Neumann代数、Banach空间标准算子代数和矩阵代数上完全保k-交换性满射的具体刻画(推论2-4)。

最后需要指出的是,由于文献[7,10]已给出素环上完全保交换性映射(即k=1的情形)的具体形式,因此本文主要讨论k>1的情形。

1 主要结果及证明

本节将讨论素代数上完全保持k-交换性映射的刻画问题,下面是本节的主要结果。

定理1 令A是实或复数域F上含单位元I的素代数,k>1是一个整数。假设Φ:A→A是满射,则下列表述等价:

(1)Φ双边完全保k-交换性。

(2)Φ2双边保k-交换性。

(3)Φ(I)∈Z(A)可逆,且存在环同构Ψ:A→A使得Φ=Φ(I)Ψ。

证明(3)⟹(1)⟹(2):显然成立。

(2)⟹(3):假设Φ2双边保k-交换性。

断言1Φ是单射。

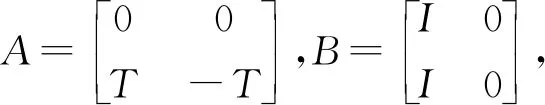
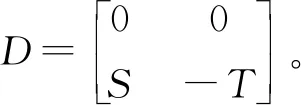
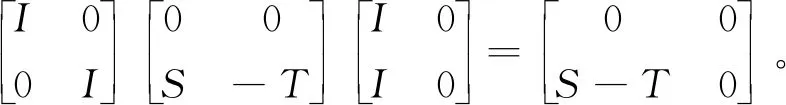
此蕴涵S=T，所以Φ是单射。

由断言1即知Φ是A上的双射。

断言2Φ(0)=0,Φ(I)∈Z(A)且在C中可逆。

首先证明:对于任意双边保持k-交换性的双射Ψ,有Ψ(Z(A))=Z(A)成立。事实上,对任意A∈Z(A),由于[A,B]k=0对所有的B∈A都成立,所以[Ψ(A),Ψ(B)]k=0.利用Ψ的满射性知[Ψ(A),T]k=0对所有的T∈A成立。由文献[14,引理2.2]即得Ψ(A)∈Z(A). 因此,Ψ(Z(A))⊆Z(A)。现由Ψ的双射性可知Ψ-1(Z(A))⊆Z(A),即Z(A)⊆Ψ(Z(A))，故Ψ(Z(A))=Z(A)。

通过简单计算易知

由于Φ2双边保k-交换性,且由Φ的双射性可知Φ2是双射,利用上面证明可知Φ2(Z(M2(A)))=Z(M2(A)),即对任意Z∈Z(A),存在Z′∈Z(A)使得

所以Φ(0)=0且Φ(Z)=Z′.特别地,0≠C=Φ(I)∈Z(A)。注意到A的素性蕴涵A的扩展中心C是一个域且Z(A)⊆C([13]).因此C在C中可逆。

现对任意A∈A,令Ψ(A)=C-1Φ(A).显然Ψ2:M2(Α)→M2(C-1Α)仍是双边保k-交换性的双射,且满足

Ψ(I)=I,Ψ(0)=0

(1)

断言3Ψ是可加的。

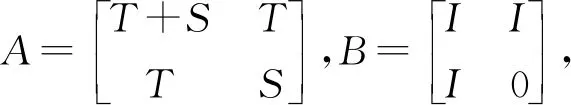
因此

(2)

其中

考虑系数α4。直接计算可得

显然α4≠0。也注意到等式(2)蕴涵α4(T+S)+α5T+α6S=0。利用T,S的任意性得

α5=α6=-α4≠0

(3)

现在对等式(2)利用Ψ2的保k-交换性以及等式(1),可得

因此,α4Ψ(T+S)+α5Ψ(T)+α6Ψ(S)=0.该式结合(3) 式得到Ψ(T+S)=Ψ(T)+Ψ(S)对任意的T,S∈A都成立。故Ψ是可加的。

由Ψ的可加性和Ψ(0)=0即得

Ψ(-T)=-Ψ(T)对所有的T∈Α都成立。

(4)

断言4Ψ是可乘的。

因而Ψ(TS)=Ψ(T)Ψ(S)对任意T,S∈A均成立,即Ψ是可乘的。

现在,Ψ的可乘性与可加性蕴涵其值域C-1A是一个环。因此C-2=C-1I·C-1I∈C-1A,即存在T∈A使得C-2=C-1T。进而有C-1=T∈A，故Ψ是A上的环自同构,且满足Φ=CΨ。

证毕。

由定理1的证明可得下面的推论成立。

推论1令A是数域上含单位元I的代数,k>1是一个整数。假设Φ:A→A是保单位元的满射,且满足Φ(0)=0，则下列表述等价:

(1)Φ双边完全保k-交换性。

(2)Φ2双边保k-交换性。

(3)Φ是环同构。

2 主要结果的应用

本节将给出第一节中主要结果的几个应用。

假设B(H)是复Hilbert空间H上全体有界线性算子构成的代数。称M是von Neumann代数,如果M是B(H)的一个C*-子代数,并且满足双换位子性质M″=M,其中

M′={T∈B(H):TA=AT,∀A∈M}

且M″=(M′)′。进一步地,若M的中心Z(M)=M∩M′=CI,则称M是因子。

注意到每个因子von Neumann代数都是素的。因此,应用定理1到因子von Neumann代数上,可得下面的推论。

推论2 令M是因子von Neumann代数,k>1是一个整数。假设Φ:M→M是满射。则下列表述等价:

(1)Φ双边完全保k-交换性。

(2)Φ2双边保k-交换性。

(3)存在非零复数c和M上的环自同构Ψ使得Φ=cΨ。

令X是Banach空间。回忆称A是标准算子代数,如果A是包含B(X)中全体有限秩算子和单位元I的B(X)的子代数。显然,A也是素代数,且其中心是FI。此外,由文献[15]可知,标准算子代数上的环同构具有形式A|→TAT-1,其中T:X→X是有界线性双射算子或者是共轭有界线性双射算子。

这样,对标准算子代数应用定理1,可得下面推论。

推论3令X是数域F上的Banach空间且A是X上的标准算子代数。假设Φ:A→A是满射，则下列表述等价:

(1)Φ双边完全保k-交换性。

(2)Φ2双边保k-交换性。

(3)存在非零数c,有界线性双射算子或共轭有界线性双射算子T:X→X使得Φ(A)=cTAT-1对所有A∈A成立。

特别地,对于矩阵代数,利用文献[9,推论3.7],可得下面推论。

推论4 令Mn是n×n矩阵全体构成的代数,k>1是一个整数。假设Φ:Mn→Mn是满射，则下列表述等价:

(1)Φ双边完全保k-交换性。

(2)Φ2双边保k-交换性。

(3)存在非零数c,数域F上的环同构τ与可逆矩阵T∈Mn使得Φ(A)=cTAτT-1对所有A∈Mn都成立,其中对于A=(aij)∈Mn,Aτ=(τ(aij))。