隐函数逻辑方程
吴金鹏
(山东省聊城大学材料科学与工程学院 252000)
一、隐函数逻辑关系
1.隐函数逻辑关系-与
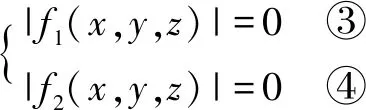
由⑤式可以看出,要使方程等式成立,当且仅当,f1(x,y,z)=0且f2(x,y,z)=0,即⑤式的取值必须同时满足f1(x,y,z)=0以及f2(x,y,z)=0.因此,⑤式的隐函数图象表示为①,②在坐标系中相交的部分.综上所述,方程⑤为隐函数逻辑关系-与.
例1推导三维空间中直线的隐函数方程.

③+④得F(x,y,z)=|A1x+B1y+C1z+D1|+|A2x+B2y+C2z+D2|=0.该方程为所需推导的三维空间中直线的隐函数方程.
当多个隐函数图象重叠时,所得图象的方程为组成该方程的隐函数的公共部分.
2.隐函数逻辑关系-或
以三元隐函数方程为例,f1(x,y,z)=0①或f2(x,y,z)=0②,若①,②为某一隐函数方程的解,则原方程为f(x,y,z)=f1(x,y,z)·f2(x,y,z)=0,方程的两解的图象在空间中互不干涉.在同一个坐标系中,两个隐函数按照自己原来的图象,依次在坐标系中.例如一个圆可以分解为两个半圆.因此,隐函数相乘为隐函数图象在空间中的叠加,所得的一个隐函数的取范围等于组成它的隐函数取值范围的和.于是f1(x,y,z)=0,f2(x,y,z)=0,f3(x,y,z)=0,…,fn(x,y,z)=0在坐标系中的叠加方程为F(x,y,z)=f1(x,y,z)·f2(x,y,z)·f3(x,y,z)·…·fn(x,y,z)=0③,③式为三元隐函数逻辑关系-或.
二、隐函数逻辑方程的梯度计算
1.隐函数逻辑方程-与的梯度计算
对于F(x,y,z)=|f1(x,y,z)|+|f2(x,y,z)|=0,由于所求得的几何图形的方程为三维空间的直线方程,因此其法向量有无数多个.此时,我们只能通过向量积运算出直线的特征向量,进而求得以该向量为法向量的平面的梯度.▽F(x,y,z)=▽f1(x,y,z)×▽f2(x,y,z).
2.隐函数逻辑方程-或的梯度计算
对于f(x,y,z)=f1(x,y,z)·f2(x,y,z)=0,可参考乘积的导数计算,于是有▽f(x,y,z)=f1(x,y,z)·▽f2(x,y,z)+f2(x,y,z)·▽f1(x,y,z)=0.
三、非等式之间的逻辑关系
非等式之间也存在两种逻辑关系,如x>5和x>4,它们在空间中的图象也具有逻辑关系.若x>5和x>4之间的逻辑关系为与时,空间中的图象表现为x>4;当x>5和x>4之间的逻辑关系为或时,空间中的图象表现为x>5.但非等式之间的逻辑关系或,与不能通过隐函数逻辑方程直接表示,因此将非等式化为等式是实现方程逻辑运算的一种选择.
1.非等式的隐函数表示

2.推导隐函数逻辑非,异或
设空间中的三元隐函数分别为,f1(x,y,z)=0,f2(x,y,z)=0.由隐函数逻辑关系-与可得F(x,y,z)=|f1(x,y,z)|+|f2(x,y,z)|=0为两隐函数的重叠部分,F(x,y,z)≠0为F(x,y,z)=0在空间R3的对立.