基于ADAMS的折臂式高空作业车展开作业稳定性分析*

王昭君，何雪浤*，周振东，谢里阳

(1.东北大学 航空动力装备振动及控制教育部重点实验室，辽宁 沈阳 110819；2.江苏东迈重工机械有限公司，江苏 昆山 215334)

0 引 言

稳定性是高空作业车辆的一个基本安全性能指标[1]。在工程实际中，因高空作业车展开过程中，发生失稳而引发的倾翻事故不仅会损坏作业车本身，也会危及工作人员的生命安全。对于折臂式高空作业车，将工作平台伸展至指定作业位置的过程中，整机的质心位置不断变化。质心在水平面的投影落入稳定区域外侧时，作业车就有发生倾覆的危险。因此，对高空作业车的展开作业稳定性进行校核至关重要。同时，在操作过程中，选取更加安全稳定的展开方式与作业顺序，也可以减小倾翻事故发生的可能性。

对高空作业车稳定性的研究已经取得很多有价值的研究成果，主要涉及作业车的整机抗倾覆稳定性、动态稳定性、结构稳定性等方面的研究。

对于静态下的抗倾覆稳定性的研究：高旭宏等[2]通过各轮胎承载的载荷特性曲线，计算出了整车的稳定性安全系数；S Palani等[3]基于力分析和重心分析方法，对自行式作业车在极限位置的稳定性进行了研究。

对于动态稳定性的研究：王君文[4]利用理论公式，计算出了极限位置下的路缘石动态稳定性安全系数；夏林焱[5]基于仿真得到了臂架结构的动态特性曲线，并分析了臂架的平稳性是否满足要求。

对于局部稳定性的分析：张珂等[6]在有限元分析软件ANSYS中，创建了起升机构的参数化模型，并对其进行了线性和非线性屈曲分析，证明了起升机构在工作状态下不会出现失稳现象。

对于影响高空作业车稳定性因素的研究：王富亮等[7]分析了转台的安装位置、支腿的横向跨距与作业臂的质量等参数对稳定性的影响；周根兵和崔金一[8]通过编程得到了不同的组合状态与任意的作业臂变幅角度下，高空作业平台稳定性安全系数；王翠英等[9]对工况变化时影响稳定性的负载和力的力矩变化进行了分析，得到了所受负载和力对稳定性的影响因子，该研究对高空作业平台的稳定性设计及应用工况起到了很好的指导作用。

以上关于起升机构稳定性的研究中，有关臂架结构伸展过程中的失稳判据与研究方法较少。基于此，本文以重力法作为研究的基本方法，利用ADAMS软件建立整车的动力学模型，对臂架结构由极限回缩状态至极限伸展状态的全行程动作进行仿真；同时分析不同展开方式及作业顺序对稳定性的影响。

1 高空作业车展开仿真过程的实现

折臂式高空作业车主要由折叠臂变幅机构、伸缩臂变幅机构、小臂伸长机构、飞臂变幅机构和调平机构等机构组成。本研究采用SolidWorks软件建立整车的装配体三维模型。

1.1 作业车结构模型及工作过程

A45折臂式高空作业车结构模型如图1所示。

图1 A45折臂式高空作业车结构模型A-底盘；B-转台；C-下臂；D-下拉杆；E-折叠臂变幅油缸；F-上拉杆；G-上臂；H-伸缩臂变幅油缸；I-伸缩臂；J-小臂；K-小臂伸长油缸；L-飞臂变幅油缸；M-飞臂；N-工作平台

折臂式高空作业车的工作过程如下：

(1)折叠臂变幅油缸E带动下拉杆D、下臂C、上臂G和上拉杆F同步运动，实现对臂架整体的升降功能；(2)伸缩臂变幅油缸H实现对伸缩臂I的升降功能；(3)小臂伸长油缸K实现对小臂J的伸缩功能；(4)飞臂变幅油缸L实现对飞臂M的翻转功能，及工作平台N的升降功能。

本研究将整车的三维模型以Parasolid格式导入至ADAMS中，并在ADMAS中对模型的零件进行合并等操作，以减少计算量；随后在各个构件之间添加约束，限制相对运动；经虚拟样机模型检验得知，系统没有冗余约束，证明模型定义基本正确。最后对折叠臂变幅油缸E、伸缩臂变幅油缸H、小臂伸长油缸K和飞臂变幅油缸L这4处液压油缸进行驱动定义，驱动函数为STEP函数，运行时间为120 s。

1.2 仿真工况及展开方式

为了体现展开过程中整机质心可能出现的极限空间位置，仿真中主要考察两种极限作业工况：最大高度作业工况和最大水平延展作业工况。最大高度作业工况指工作平台伸展至最高极限位置，最大水平延展作业工况指工作平台伸展至最远极限位置。

两种极限作业工况如图2所示。

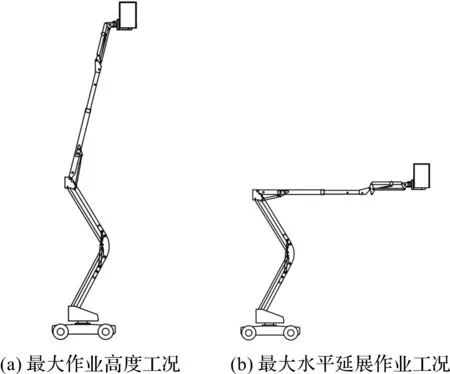
图2 两种极限作业工况

不同的展开方式对展开作业稳定性的影响不同，本次仿真针对上述两种工况选用工程实际中常用的两种展开方式进行校核，分别是同步展开和顺序展开。同步展开表示各个作业臂之间同时进行动作，顺序展开则表示各个作业臂之间依次进行动作。

2 高空作业车展开作业稳定性分析

2.1 质心轨迹求解程序

依照重力法原则[10]，从前支点到后倾翻线距离的80%为稳定区域，高空作业车的重心在水平面上的投影位置应不超过该稳定区域，即高空作业车在展开过程中，整机的质心轨迹在水平面上的投影始终落入稳定区域内，则展开作业稳定性满足要求。

对于本文选取的A45折臂式高空作业车，已知前后轴倾翻线之间的距离l为2 000 mm，在倾覆线中心点位置建立坐标系，倾覆线以内80%区域为稳定区域。

折臂式高空作业车倾覆线内稳定区域如图3所示。

图3 折臂式高空作业车倾覆线内稳定区域

在臂架结构展开过程中，若要保证整机的稳定性，整机质心的横向偏距最大值xmax不得大于稳定区域的界限值，即：

(1)

已知在ADAMS/VIEW的后处理中，仅能得到各个组成部件仿真后的质心坐标，但判定展开作业稳定性所需要的整机质心坐标并不能直接得到。因此，此处引入系统质心的求解公式。

质点系质心C在直角坐标系Oxyz中的坐标可以表示为：

(2)

式中：M—质点系的总质量；mi—质点系中质点的质量；xi—质点mi相对于直角坐标系Oxyz的坐标。

基于质心求解原理，即式(2)，编写质心轨迹求解程序，该程序可以计算并记录折臂式高空作业车展开过程中，整机质心坐标值的变化过程。

具体步骤为：首先建立系统状态变量和坐标设计变量，然后通过for循环对模型中的部件进行遍历，查找获取模型部件的总质量和质心x方向的坐标值，最后将该程序保存为后缀名为.cmd的文本文件[11]。

实现仿真后，导入并运行质心轨迹求解程序，在后处理中导出整机的质心坐标，以此分析并确定臂架结构展开过程中，是否会发生倾覆[12]。

2.2 最大高度作业工况及其稳定性分析

本研究对高空作业车臂架结构伸展至最高极限位置的过程进行仿真，展开方式分别为同步展开与顺序展开。导入质心轨迹求解程序，得到整机的质心坐标值，并在Matlab中进行质心横向偏离曲线的绘制。

伸展至最高极限位置过程中质心横向偏离轨迹如图4所示。

图4 伸展至最高极限位置过程中质心横向偏离轨迹

图4中，点A、B、C、D分别表示以顺序动作伸展至最高极限位置的过程中，折叠臂变幅油缸、伸缩臂变幅油缸、小臂伸长油缸和飞臂变幅油缸依次开始作用的时间。

由图4可知，在工作平台伸展至最高极限位置的过程中，展开方式为同步展开时，整机质心横向偏距最大值xmax1为578.22 mm；展开方式为顺序展开时，整机质心横向偏距最大值xmax2为468.16 mm。且有：xmax1<800 mm；xmax2<800 mm。

由此说明，高空作业车在以上述两种展开方式伸展至最高极限位置的过程中，质心在水平面上的投影始终落入稳定区域，即高空作业车没有发生倾覆的危险，整车具有良好的展开作业稳定性。

2.3 最大水平延展作业工况及其稳定性分析

本研究对高空作业车臂架结构伸展至最远极限位置的过程进行仿真，展开方式分别为同步展开与顺序展开。

伸展至最远极限位置过程中质心横向偏离曲线如图5所示。

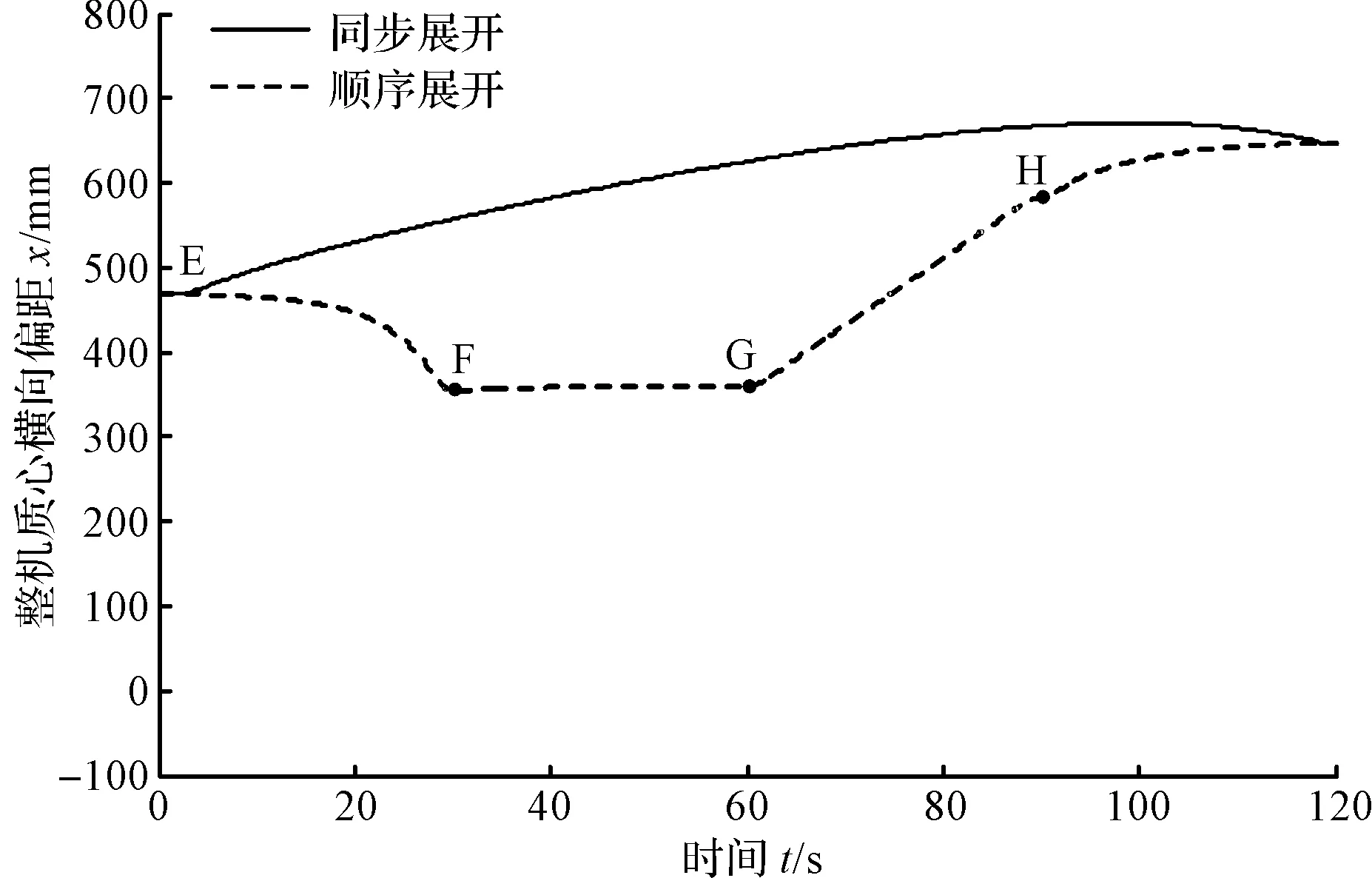
图5 伸展至最远极限位置过程中质心横向偏离曲线

图5中，点E、F、G、H分别表示以顺序展开方式伸展至最远极限位置的过程中，折叠臂变幅油缸、伸缩臂变幅油缸、小臂伸长油缸和飞臂变幅油缸依次开始作用的时间点。

由图5可知，工作平台伸展至最远极限位置的过程中，展开方式为同步展开时，整机质心横向偏距最大值xmax3为670.83 mm；展开方式为顺序展开时，整机质心横向偏距最大值xmax4为645.51 mm。且有：xmax3<800 mm；xmax4<800 mm。

由此说明，高空作业车在以顺序展开和同步展开方式伸展至最远极限位置的过程中，质心在水平面上的投影始终落入稳定区域，整车没有发生倾覆的危险，也具有良好的展开作业稳定性。

2.4 两种不同展开方式的对比

在2.2和2.3节中已经证明了在顺序展开与同步展开方式下，臂架结构伸展至极限位置过程中的稳定性满足作业要求，现分别以顺序和同步展开方式将工作平台伸展至最高和最远极限位置，以对比这两种展开方式下的质心横向偏离曲线。

顺序及同步展开至极限位置过程中质心横向偏离曲线如图6所示。

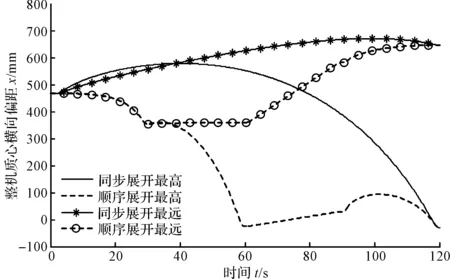
图6 顺序及同步展开至极限位置过程中质心横向偏离曲线

由图6可以看出，顺序展开方式下的质心横向偏移距离相对小于同步展开方式下的偏移距离；同时在顺序展开过程中，整机质心处在横向危险位置的时间比同步展开要少。

综上所述，相比于同步展开，以顺序展开的方式操作高空作业车会更安全，稳定性也更高。因此，在工程实际操作条件允许的前提下，工作人员应尽量避开同步展开作业方式，应选择以顺序展开的作业方式将作业平台伸展至工作位置。

3 基于作业顺序的稳定性分析

为了进一步提高高空作业车臂架展开过程中的安全性及稳定性，本节在顺序展开的基础上，探讨可以使展开过程更稳定的作业顺序。笔者选取两种情况进行研究分析：(1)自上而下与自下而上展开作业顺序，(2)先伸长后变幅与先变幅后伸长展开作业顺序。选取的工况为最大高度作业工况，限于篇幅原因，对仿真过程不再详述。

3.1 自上而下与自下而上展开作业顺序

笔者在高空作业车臂架结构伸展至最高极限位置的过程中，分别以自上而下和自下而上的展开作业顺序进行运动学仿真，后处理得到整机质心的横向偏离曲线。

自上而下与自下而上作业顺序下质心横向偏离曲线如图7所示。

图7 自上而下与自下而上作业顺序下质心横向偏离曲线

由图7可知，高空作业车臂架结构以自上而下的顺序展开时，整机质心横向偏距最大值xmax5为628.85 mm；臂架结构以自下而上的顺序展开时，整机质心横向偏距最大值xmax6为468.16 mm。且有：

xmax5<800 mm；xmax6<800 mm。

由此说明，高空作业车在以自上而下和自下而上的展开作业顺序伸展至最高极限位置的过程中，没有发生倾覆的危险，展开作业稳定性得以保证。

同时可以看出，相比于自上而下的展开作业顺序，自下而上展开作业过程中的质心横向偏移距离相对更小，且其处于横向危险位置的时间也较短，所以自下而上展开作业顺序更趋向于稳定。

综上所述，在工程实际中，自下而上展开作业顺序较安全，稳定性也更高。

3.2 先伸长后变幅与先变幅后伸长展开作业顺序

本研究通过调整驱动函数，在高空作业车臂架结构顺序伸展至最高极限位置的过程中，分别以先伸长后变幅和先变幅后伸长的作业顺序进行运动学仿真，绘制整机质心的横向偏离曲线。

先伸长后变幅与先变幅后伸长作业顺序下质心横向偏离曲线如图8所示。

图8 先伸长后变幅与先变幅后伸长作业顺序下质心横向偏离曲线

由图8可知，臂架结构先变幅后伸长时，整机质心横向偏距最大值xmax7为468.16 mm；臂架结构先伸长后变幅时，整机质心横向偏距最大值xmax8为693.90 mm。且有：xmax7<800 mm；xmax8<800 mm。

由此说明，高空作业车在以先伸长后变幅和先变幅后伸长的作业顺序伸展至最高极限位置的过程中，没有发生倾覆的危险，展开作业稳定性得以保证。

同时可以看出，相比于先伸长后变幅的展开作业顺序，先变幅后伸长展开作业过程中的质心横向偏移距离更小，且其处于横向危险位置的时间也较短，所以先变幅后伸长展开作业顺序更趋向于稳定。

综上所述，在工程实际中，先变幅后伸长的展开作业顺序较安全，稳定性也更高。

4 结束语

针对当前对于臂架结构伸展过程中的失稳判据与研究方法较少的现状，本文结合ADAMS软件，一方面提出了一种通过仿真与重力法相结合的方法，对作业臂的展开作业稳定性进行了分析，另一方面对比了不同的展开方式及作业顺序对稳定性的影响，有助于在工程实际操作中选取更加安全的执行方式。研究结论如下：

(1)A45折臂式高空作业车在以顺序和同步动作伸展到最高和最远极限位置的过程中，整机质心的横向偏距均小于800 mm，没有发生倾覆的危险，整车具有良好的展开作业稳定性。

(2)臂架结构伸展至极限位置的过程中，相比于同步展开，顺序展开方式具有更高的稳定性。

(3)以顺序展开方式伸展至最高极限位置的过程中，各作业臂以自上而下、先变幅后伸长的顺序动作时，整机具有更高的稳定性。