涪陵页岩气田集气干线积液规律研究*

中国石化重庆涪陵页岩气勘探开发有限公司

涪陵页岩气田位于山地丘陵地带，由于集气站内重力分离器气液分离效果差、管线温压变化大、起始管段气量低、管线起伏高差大等因素影响，天然气中携带的游离液和析出的饱和液易沉积在管线低点无法带出，降低了集气干线输气效率，增大了腐蚀风险[1-3]。目前气田主要采用放喷和清管等措施进行排液，既存在天然气浪费，又存在清管降产，影响气田生产任务完成。因此，有必要开展集气干线积液规律研究，建立管线临界携液流速及积液量计算方法，准确认识管线积液情况，有效保障集气干线安全、高效地运行。

1 倾斜管气液两相流动模拟

1.1 模型描述

通过对管道内气液两相流动仿真模拟，研究集输管道内的积液规律。涪陵页岩气田目前已建成70×108m3/a集输工程，集气干线规格主要有Φ 559 mm×10 mm、Φ 457 mm×10 mm、Φ 323 mm×10 mm、Φ353 mm×9 mm四种。

本次模拟采用规格为Φ457 mm×10 mm的管线，管线内径为437 mm，管线压力为5 MPa。考虑计算长度（1～10 m）内温度变化不大（小于1 ℃），可以忽略，不考虑流体相变，流体流动为不可压缩稳态流动。

采用Gambit软件绘制三维结构网格模型，管线入口端水平段长为2 m，出口端倾斜段长为6 m，弯管曲率半径为1.5D，对网格处理好边界形状，并且在流动参数变化大的弯管区域适当加密网格，如图1所示。

图1 管道模型建立与网格划分Fig.1 Pipeline model establishment and meshing

利用Fluent软件模拟管线内气液两相流动，其中两相流模型选择Eulerian模型，用以描述管道中液体的液滴态和液膜态；对于流动中有相混合或分离的流动，Eulerian模型能给出更精确的结果。气体和液体入口边界采用速度边界，出口边界采用压力出口，湍流模型选择RNGk-ε模型，用以处理高应变率及流线弯曲程度较大的流动。

1.2 模拟结果

设定入口速度为1 m/s，持液率为0.2，倾斜段角度为45°进行模拟，选取y=0截面进行分析，气体携带液体经过弯管进入倾斜管段时形成湍流（图2），造成气体动能损失，气体流速降低（图3），无法举升液体，造成液体回落（图4），滑脱损失增加，倾斜段压力梯度增加（图5）。

图2 湍流强度分布云图Fig.2 Distribution cloud chart of turbulence intensity

图3 速度分布云图Fig.3 Distribution cloud chart of velocity

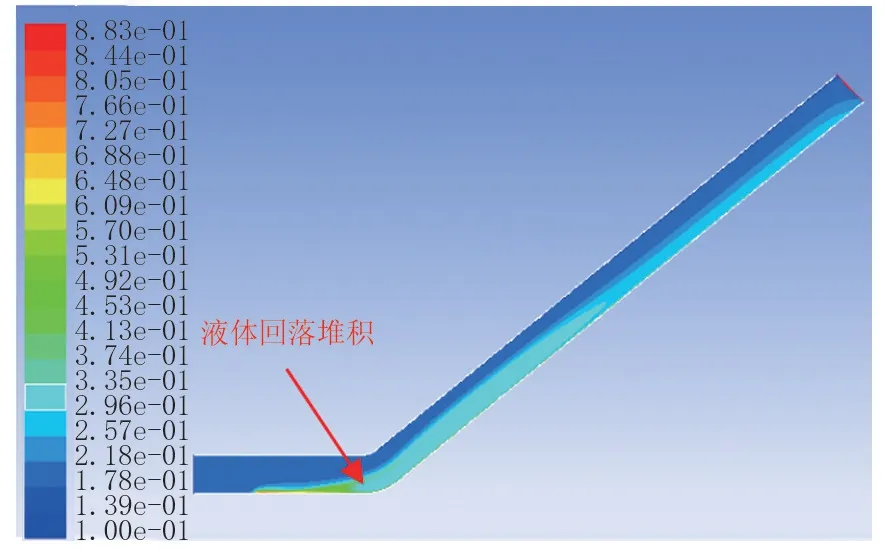
图4 含水率分布云图Fig.4 Distribution cloud chart of water content

图5 压力分布云图Fig.5 Distribution cloud chart of pressure

设定入口持液率为0.2，入口速度分别为0.5、1、2、3 m/s，倾斜管段角度分别为30°、45°、60°，模拟不同气体流速、不同倾斜角度时管道积液的规律，如表1、图6所示。当倾斜管角度一定时，气体流速越快，管道内的平均持液率越低，说明管道中滞留的液体越少；相同流速下，45°倾斜角携液能力最差，管道内平均持液率最高，管道内滞留的液体最多，说明45°倾斜角所需的临界携液流速最大。

表1 不同流速、不同角度倾斜管含水率分布对比Tab.1 Comparison of water content distribution in inclined pipes with different flow velocities and angles

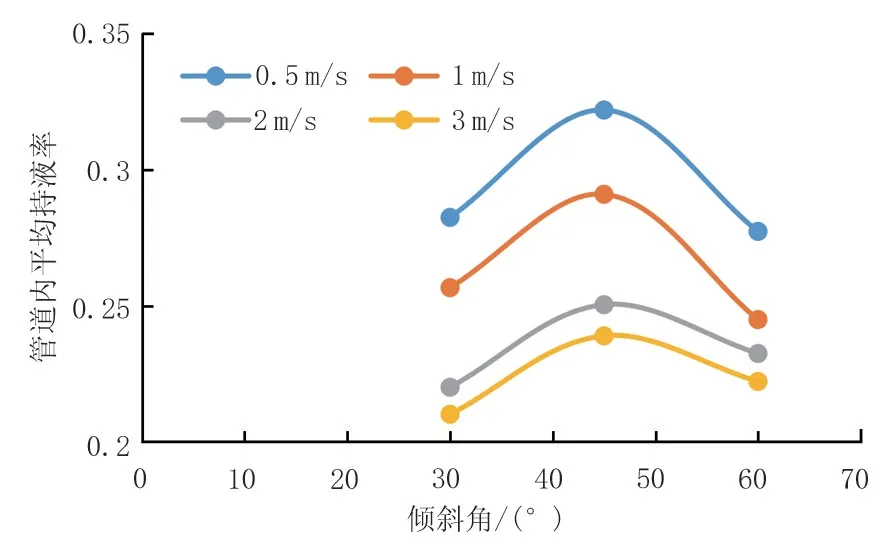
图6 不同倾斜角度、不同流速下管道内平均持液率对比Fig.6 Comparison of average liquid holdup in pipeline with different inclination angles and flow velocities

2 临界携液气量计算

目前主流的携液模型有两种：一种是基于液滴模型假设，认为排出气井积液所需的最低条件是使气流中最大液滴能连续向上运动；另一种是基于液膜模型假设，液膜模型认为液膜的反向流动是导致积液的主要原因[4]。根据模拟结果分析，当流速增大至临界携液流速以上，液体由扰动流逐渐向环状流转化，液体生成后，在向上移动的同时逐渐向管壁靠近，最终与管壁的液膜融合在一起，并不能稳定存在，因此认为倾斜管的液体主要以液膜形式被携带。

肖高棉等[5]认为液膜向上流动是由运动气流作用于气液界面产生的剪切力τi克服液体重力与管壁剪切力τw的结果，如图7所示。

图7 液膜受力分析示意图Fig.7 Schematic diagram of liquid film force analysis

当气液界面剪切力τi与液膜重力达到平衡时，液膜与管壁间剪切力τw趋于0，液膜厚度达到临界值δcr，液膜开始出现反向流动，此时的气体流速为倾斜管临界携液流速，根据受力分析

式中：τi为气液界面剪切力，N/m2；ρl为液体密度，kg/m3；g为重力加速度，m/s2；δcr为临界液膜厚度，m；θ为管段的倾斜角，（°）。

根据沿程阻力的概念，忽略液速的影响，气液界面产生的剪切力τi可用下式来计算

式中：fi为气液界面摩阻因数；ρg为气体密度，kg/m3；vg为气体流速，m/s。

fi可用Wallis[6]计算式求得

式中：D为管道内径，m。

综合（1）式和（2）式可获得临界携液流速表达式

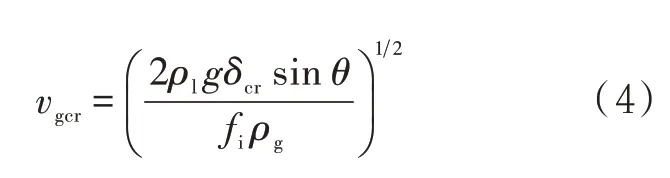
式中：vgcr为临界携液流速，m/s。

考虑倾斜管中液膜不均匀分布，PAZ[7]将圆管简化为正方形进行研究，如图8所示。根据实验观测的数据，认为小角度倾斜管（0～60°）中，管道底部液膜厚度明显大于管道顶部和边缘的液膜厚度，而对于大角度倾斜管（60°～90°），液膜在底部和管壁边缘更厚，在顶部较薄。

图8 倾斜管液膜分布Fig.8 Liquid film distribution in inclined tube

对于小角度模型，假设在方形管道的顶部和两边液膜均匀厚度为δfT，底部液膜厚度为δfB，PAZ[7]基于沿轴向单位长度上底部液膜的质量守恒，给出了δfT与δfB的关系式（5）以及δfT与持液率Hl的关系式（6）

式中：因数N的表达式[4]为

对于大角度倾斜管，管道侧面的液膜厚度与底部的液膜厚度相同，为δfB，管道顶部的液膜厚度为δfT，基于顶部液膜质量守恒关系，推导出大角度倾斜管液膜分布表达式为

持液率计算选用Beggs&Brill-Moody模型，在Beggs-Brill持液率修正模型中，引入了倾角修正系数ψ，表示倾斜管截面持液率与水平管截面持液率的比值[8]。

式中：Hl(θ)为倾角为θ时的截面持液率，无因次；Hl( 0 )为水平管截面持液率，无因次。

水平管截面持液率Hl( 0 )取决于体积含液率Rl和弗劳德数Fr。

式中：Ql为液相的质量流率，kg/s；Qg为气相的质量流率，kg/s；vm为气液混合物速度，m/s；a、b、c均为与流型有关的系数；C为常数。

将液膜分布方程与临界携液流速计算方程耦合计算可获得管道气体临界携液流速计算模型，该模型考虑液膜在周向上的不均匀分布。利用液膜分布模型计算最大液膜厚度，将其代入临界携液流速计算方程，即可计算临界气流速度。求解过程如下：

（1）给定气体流速初值vg0。

（2）利用vg0求出持液率Hl。

（3）将Hl代入液膜分布计算方程中，计算管道最大液膜厚度δf。

（4）将计算获得的δf代入临界携液流速方程获得vg1。

（5）将vg1与vg0比较，若在误差允许范围内，则vgcr=vg1为临界携液流速；否则令vg0=vg1，重复步骤（2）～（4），直到满足误差要求。

根据以上方法计算管线规格为Φ457 mm×10 mm的临界携液流速，管线输压为4 MPa时，管内气体临界携液流速随倾斜角的变化如图9所示。倾斜角为50°左右时所需的临界携液流速最大，携液最困难。

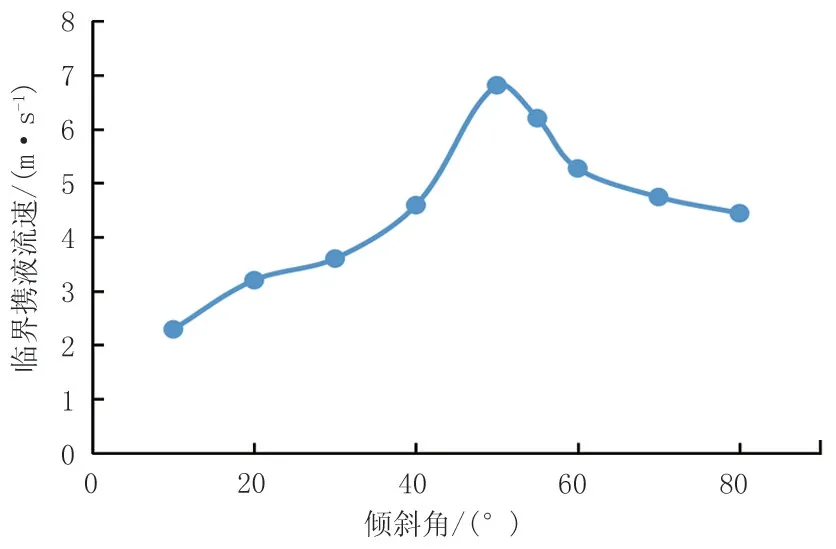
图9 不同倾斜角临界携液流速（ D=437 mm， p=4 MPa）Fig.9 Critical liquid-carrying velocity at different inclination angles ( D=437 mm， p=4 MPa)

3 集输管线积液量计算

天然气在流动过程中，一方面随着管道与周围环境之间的热交换，温度会降低，在一定的温度、压力条件下一部分液体会凝析出来，此时管路内形成气液两相流[9]；另一方面，对于产气量大、产水较高的集气站，可能因站内分离不彻底，导致气体携带部分液态水进入管网，这种情况下管线内气体携液量无法准确得知。积液管段积液量可通过沿程持液率计算[10]。

式中：QL为管线内总积液量，m3；L为管线长度，m；A为管线截面面积，m2。

当管道中液体流量无法获得时，持液率Hl很难准确计算。本文引入最优化算法，在已知单段管线进出口压力和输气量的前提下，利用遗传算法，以管线计算压差与实际压差误差最小为优化目标，拟合管线液体流量，从而获得积液管段积液量。计算流程如图10所示。

图10 积液量计算流程Fig.10 Calculating process of liquid loading volume

4 实例分析

涪陵页岩气田DN450集气干线A—H段全长15.2 km，管线规格为Φ457 mm×10 mm，位于山地丘陵地带，管道起伏较大，如图11所示。该段管线于12月9日开展清管作业，共清出积液95 m3。从各节点压力变化（图12）分析可知，清管后除末端节点压力有所升高外，其余节点压力均降低，整段管线压差减小。从集气干线各段输气量（图13）分析可知，清管后各段输气量均有所增加，G—H段输气量由390×104m3/d上升至440×104m3/d。

图11 A—H段管线沿程海拔Fig.11 A—H elevation along pipeline

通过集气干线临界携液气量模型及积液量计算模型对A—H段干线进行计算分析，获得各段管线临界携液气量变化曲线如图14所示。A—B段、C—D段存在明显的爬坡，所需携液气流速度较大。输气量无法达到临界携液气量时，产生积液如图15所示。C—D段清管前因输压较高，输气量低于临界携液气量，产生积液；清管后，排除了管线积液，降低了C、D节点输压，释放气井产能，管线输气量增加，提高了C—D段管线携液能力。A—H段清管前后积液量变化如图16所示，计算得到清管后排除积液101 m3，实际清管清出积液95 m3，证实了模型的有效性。

图12 各节点压力随时间的变化Fig.12 Variation of node pressures over time

图13 集气干线各段输气量随时间的变化Fig.13 Variation of gas flow with time in each section of gas gathering trunk line

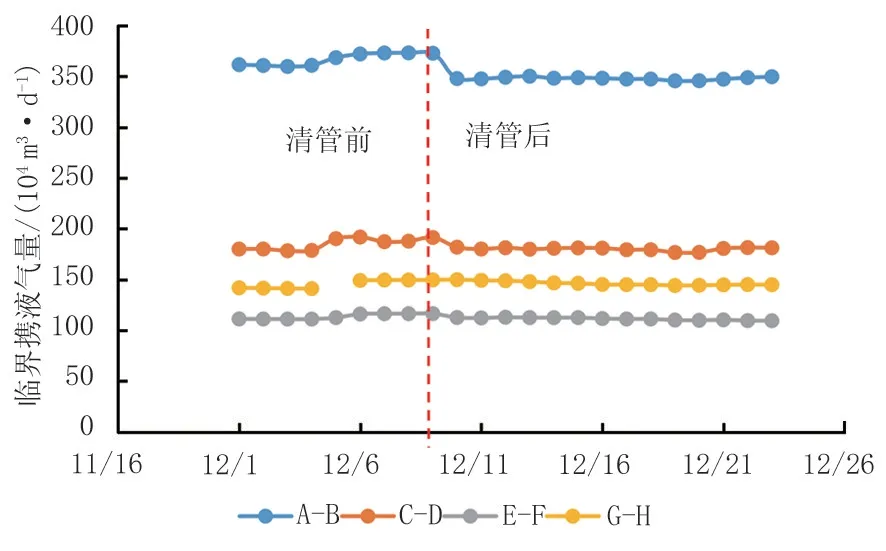
图14 各段管线临界携液气量对比Fig.14 Comparisons of critical liquid-carrying capacity of each section

图15 C—D段积液量分析Fig.15 Analysis of liquid loading volume in C—D section

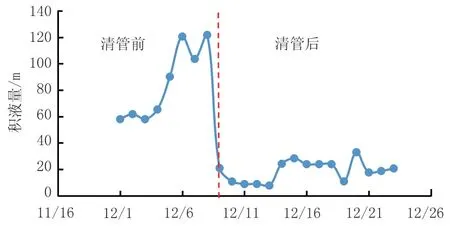
图16 A—H段干线清管前后积液量随时间的变化Fig.16 Liquid loading volume changes with time of A—H trunk line before and after pigging

5 结论与认识

（1）倾斜管段液膜的反向流动是导致积液的主要原因，倾斜角为50°左右时需要的临界携液流速最大。

（2）在基于液膜流动的临界携液流速模型的基础上引入遗传算法，推导的积液量计算方法适用于涪陵页岩气田集气干线。

（3）涪陵页岩气田A—H段干线积液主要发生在输气量较小、倾斜角较大的A—B段和C—D段，建议加强该段干线沿线集气站管理，通过管网输气量调控解决管线积液问题，延长集气干线清管周期。