基于人工鱼群优化的BP神经网络WiFi指纹室内定位方法

邓素,薛峰,余敏

(江西师范大学 计算机信息工程学院,江西 南昌 330022)

0 引 言

随着移动计算、无线定位等技术的迅速发展和普及,基于“位置的服务”(LBS)正向我们展现出广阔的市场应用前景．自美国在1996年通过著名的E911法案,美国联邦通信委员会强制要求各电信运营商开发出能够在紧急救援事件中为社会安全机构提供用户的位置信息,定位技术越来越被人们所关注．定位按照使用场景的不同可划分为室内定位和室外定位两大类．在室外,人们主要依靠全球定位系统(GPS)、格洛纳斯定位系统(GLONASS)、北斗卫星导航系统(BDS)来获取可靠、实时的位置信息．而进入室内,由于建筑物对卫星信号的遮蔽,全球卫星导航系统(GNSS)终端在室内或者建筑物密集的室外便很难获取到卫星信号,难以满足室内服务应用对定位精度的要求,因此GPS等定位系统并不适用于室内．所以为解决这个问题,科研人员将注意力转移到了无线传感网．相比于射频识别技术(RFID)、超声波、红外、超宽带(UWB)等需要依赖部署专用的硬件设施应用范围有限且成本昂贵的定位技术,无线WiFi定位技术凭借着其覆盖范围广、实现简单、部署难度低、无需额外成本等优点而被广泛运用．

无线室内定位算法主要可分为两大类:基于测距的定位和基于非测距的定位．基于测距的定位方法主要有到达时间(TOA)、到达时间差(TDOA)、到达角(AOA)等．基于非测距的定位方法主要是基于接收信号强度值,该方法可分为指纹匹配法和距离路径衰减模型法．室内指纹匹配定位技术因其非视距、定位精度高、受室内环境影响小、实现灵活等优点备受人们的关注．

近年来,关于WiFi无线定位方式的研究,张会清[1]提出了一种用BP神经网络来拟合室内无线信号的传播模型．邓胡滨[2]提出一种利用广义回归神经网络(GRNN)拟合室内信号强度指示(RSSI)值与距离值的映射关系,得到相应的定位模型方法．黄丰胜[3]通过分析在不同场景下基于RSSI指纹匹配法和位置估计法,验证了指纹匹配法具有更高的定位精度．李瑛等[4]提出了一种基于反向传播(BP)神经网络的室内定位模型,与基于信号衰减模型的定位算法测试对比后,结果表明利用BP神经网络进行室内定位能获得更好的定位精度,但此方法在进行BP神经网络的初始化训练时,由于神经网络参数值的随机选取,导致节点表现出个体差异,部分节点的定位精度始终较低．闫思锐[5]通过分析无线通信模型,针对室内无线信号传播模型中路径损耗指数和参数依据经验判断导致的定位误差太大问题,提出利用BP神经网络拟合RSSI-d非线性函数关系,大大降低了定位误差．但由于室内环境的复杂多样性,存在多径效应,会导致信号强度波动较大,传播模型距离估算不准确,进而定位精度受到了极大的影响[6]．针对以上问题,为提高无线网络室内定位的效果,本文将改进的人工鱼群优化算法和BP神经网络[7]WiFi指纹室内定位算法相结合,首先利用改进的人工鱼群优化算法对神经网络的权值和阈值参数进行优化[8-9],改善了人工神经网络的预测值易陷入局部最低等缺点．然后再将优化后的BP神经网络学习RSSI和两维位置信息间的非线性映射关系,可有效提高定位精度以及算法的收敛速度和可靠性．

1 室内定位算法原理

1.1 基于信号强度的测距模型

自由空间传播模型是指在发送端与接收端之间不存在障碍物的干扰且是在视距(LOS)状态下的接收信号模型[10]．是一种简单的无线电传播模型．依据无线通信原理,信号的接收功率与发射功率的关系可表示为:

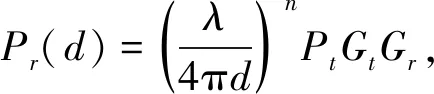
(1)

式中:Pt为信号源的发射功率；Gt、Gr分别为天线在发送和接收信号时的增益；λ为无线电信号波长；Pr(d)为接收端距发射端d处时的接收功率．一般情况下,用RSSI来推算距离时,可由经验路径模型得出,即:

RSSI(d)=A-10nlg(d),

(2)

式中:d为待测定位点的距离;A为距离信号发射源1 m处接收到的信号强度平均值的绝对值;n为路径损耗系数．

1.2 基于WiFi信号指纹(fingerprinting)的定位

WiFi信号除了以接收信号强度(RSS)传播模型为主的测距定位方法外,现运用更多的方法是通过指纹方式实现定位．指纹定位包括两个阶段:训练阶段(offline)和服务阶段(online)．训练阶段对数据进行采样,将收集的无线信号特征存入数据库．在服务阶段,使用数据库中的RSSI和当前的RSSI值进行对比和定位．确定性算法、概率性算法和人工神经网络算法是目前常用的待测定位点的估计方法．

在设计BP神经网络时,考虑到RSSI值易受环境影响,波动较大,若采用基于信号强度的测距模型来进行定位,由于其中距离是由RSSI推算出来的,在计算过程中将会丢失一些原始信息,而且一般情况下,室内通常存在噪声,所以本文将把RSSI平均值作为BP神经网络的输入,为减少数据采集过程中的误差,在采集RSSI数据值时采用高斯滤波进行处理,将待定位节点的坐标作为输出来进行BP神经网络训练,并建立如下函数关系:

φ(RSSI1,RSSI2,…,RSSIn)=(x,y),

(3)

其中,RSSIi,i∈(1,n)为目标定位节点接收来自各信标定位节点的的RSSI．

2 基于双隐层BP神经网络训练指纹定位模型

BP神经网络[11-12]是一种按误差逆传播算法训练的多层前馈网络,也是一种监督学习型人工神经网络,具有很强的非线性映射能力．常用于函数逼近、模式识别等预测学习领域．BP神经网络学习过程由信号的正向传播与误差的反向传播两个过程组成．典型的BP神经网络通常包括三层结构:输入层,隐含层,输出层．输入层神经元负责接收外界输入信息,并传递给隐含层,隐含层(可分为单隐层或多隐层)负责当完成信息加权聚合变换和正向传播处理后,通过输出层向外界输出处理结果．当实际输出值与期望输出值不符时,进入误差反向传播阶段．通过三层BP神经网络可以拟合任意的连续非线性曲线,但本文中坐标值与RSSI值之间的对应关系并不连续,属非线性关系．根据实验条件和相关定理及经验得知,本文选择使用四层神经网络．其中包括2个隐含层,1个输入层和1个输出层．第一层传递函数为sigmod函数,第二层传递函数为线性函数．模型如图1所示.

仅仅使用BP神经网络进行网络训练容易陷入局部极小化,且该网络的收敛速度慢,对初值和网络权重十分敏感．人工鱼群算法具备全局的寻优能力,能快速跳出局部极值点,另外还具有较快的收敛速度,对初始值要求不高的特点,本文将利用改进的人工鱼群算法来优化神经网络别的初始权值和阈值．完成神经网络的训练并改进其性能．

图1 BP神经网络模型结构

3 改进的人工鱼群算法优化BP神经网络参数

3.1 人工鱼群算法

人工鱼群算法是一种采用自上而下的新型的群智能寻优策略算法,是一种动物自治体优化方法．该算法通过单个个体的局部寻优,从而达到全局最优．其核心思想主要是通过初始化构造单条人工鱼模拟自然界中鱼群的觅食、聚群、追尾、随机、移动等行为,不断地进行自我迭代位置更新,先从局部进行搜索寻优,然后再在各自组织中进行消息传递,从而实现全局寻优．

在一片水域中,鱼总是能自行或者尾随其他鱼找到食物最多的地方．通过模拟鱼群的这种行为,可将人工鱼群算法分为四个行为:觅食行为、聚群行为、追尾行为、随机行为．假设当前人工鱼l的状态用状态向量表示为Xl=(x1,x2,x3,…,xn),Yi=φ(Xl)为人工鱼当前所在位置的食物浓度,Xl为待优化变量,即是Xl的适应度函数;δ为拥挤度因子,S为人工鱼移动步长,V为人工鱼的视野范围,n为视野内人工鱼数目.trynum为最大尝试次数,R为最大迭代次数．算法实现描述如下．

3.1.1 觅食行为

假设人工鱼当前状态为Xh,在其视野范围V内随机选择一个状态Xl,则有:

Xl=Xh+V·Rand(),

(4)

式中,Rand()为一个产生介于0～1之间的随机函数,V是视野范围,若Yl>Yh,则人工鱼按式(5)向前移动一步,否则,再重新选择随机状态Xl,判断是否满足前进条件,如此重复尝试达到trynum次后,若仍不符合条件,则按照式(6)随机移动一步．

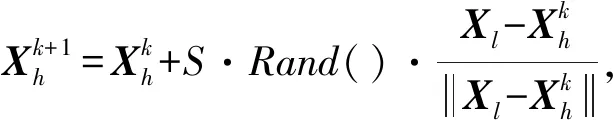
(5)

(6)

3.1.2 聚群行为

自然界中,鱼在游动过程中,为保证群体生存,躲避危害,会自然聚集成群．假设人工鱼当前状态为Xh,探索领域内伙伴数为n,中心位置为Xc,若Yc/n>δYh,表明中心位置食物较多且不拥挤,这时则向中心位置前进一步,否则执行觅食行为．

(7)

3.1.3 追尾行为

假设人工鱼m当前状态为Xm,Xz是视野范围内能找到的最好的位置,若Yz/n>δYm,表明伙伴Xz周围食物浓度高且不太拥挤．则按式(8)向前移动一步．

(8)

3.1.4 随机行为

人工鱼在视野中随机选择一个状态,然后朝该方向运动,它是觅食行为的一个缺省行为．

3.2 基于改进的人工鱼群算法的BP神经网络

基本的人工鱼群算法是存在缺陷的,算法的精度与人工鱼的步长S和视野范围V关系较大．常规的算法中,步长S是个定值,但是当步数逐渐增加时,算法收敛速度将会加速,当超过一个范围后,收敛速度又将会减慢,当S较小时,振幅较小,精度相对较高,当S较大时,振幅较大,精度较差．这将造成算法在前期收敛速度快,后期收敛速度缓慢,且会伴有震荡现象产生．因此,本文对该算法的步长S和视野V按照式(9)做了相应的改进．为尽量避免上述现象的发生,本文采用一种自适应步长的策略．

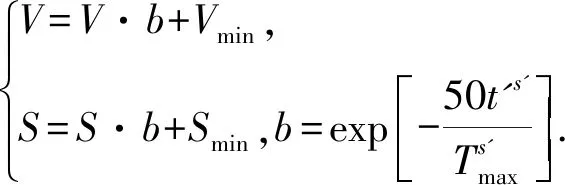
(9)

式中：b为误差迭代函数,表征迭代速度；Tmax为最大迭代次数；t'为当前迭代次数；s'为[1…60]的整数；S为步长；V为视野范围．

3.2.1 IAFSA优化的BP神经网络

改进的人工鱼群优化BP神经网络算法(IAFSA-BP)的主要核心思想是通过IAFSA找到BP神经网络的最优参数．人工鱼的位置Xl=(1,2,3,…，q)对应了BP神经网络的一组参数,q为搜索空间维数,对应BP神经网络的权值和阈值．笔者在本文中主要采用了双隐层神经网络,设输入层神经元个数为m,第一隐层神经元个数为g,第二隐层神经元个数为e,输出层神经元个数为f,则有:

q=m(g+1)+ge+(e+1)f.

(10)

人工鱼的一个状态值Xl表示一个神经网络的阈值和权值．使用IAFSA反复优化BP网络模型的参数组合,直到解的适应度不再发生改变．BP神经网络均方差误差函数为

(11)

式中：n为训练样本集维数；yi为网络实际输出；ξ为输出节点数量；hk为目标输出；F的倒数为人工鱼所处环境的食物浓度．从上述模型中,本文设置V=2.0,S=0.2,拥挤度因子δ=0.618,N=10,trynum=50,R=300,Vmin=0.01,Smin=0.002,Tmax=500,根据经验参考公式设置BP神经网络第一隐层神经元数为N2=8,第二隐层神经元数为N3=4,输入层节点数为5,输出层节点数为2,网络模型结构为4-8-4-2．流程图如图2所示.

图2 IAFSA-BP室内定位算法流程图

4 方案设计与分析

4.1 实验环境

本文的实验环境在江西师范大学先骕楼七楼3705工作室,试验区域面积为10 m×10 m,并且按照1.0 m×1.0 m的规格将试验区域划分为100个小网格,无线AP型号采用TP-Link TL-WR885N,现场共布设4个AP终端设备,AP距离地面高度为1.5 m．定位区域平面示意图如图3所示,移动采集终端设备为华为mate10pro,共采集80个采样点,在每个采样点采集20次RSSI值．并用高斯滤波处理去噪后再利用加权均值的方法求出RSSI平均值,与采样点的地理位置坐标一同构成集合{x,y,RSSI1,RSSI2,…,RSSIn}.

图3 定位实验平面区域图

4.2 实验分析

为验证本文定位算法的稳定性和有效性,本文运用基于粒子群优化的BP神经网络算法(PSO-BPNN),BP神经网络算法(BPNN),以及本文提出的IAFSA-BPNN无线WiFi指纹定位算法进行训练和实验,模型训练的数据均为在工作室实验区域统一采集的数据．本文采用留出法将数据集划分为两部分,一部分作为训练集,另一部分作为测试集．并将神经网络的输出位置值与原参考点进行比较,统计其定位误差,表1为使用各算法得到的定位性能统计表．

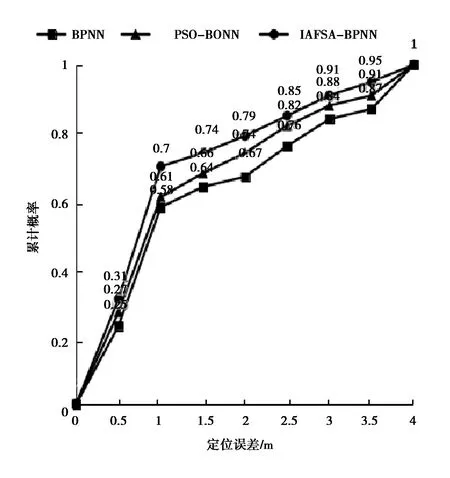
图4 三种方法定位性能对比

通过图4可看出,本文提出的人工鱼群优化的双隐层BP神经网络WiFi指纹室内定位算法在0～1 m,1～2 m的定位误差比PSO-BPNN,BPNN的误差概率均要高,分别为70%和9%,在2 m内的误差累积概率可达79%,充分说明了IAFSA-BPNN无线WiFi室内定位算法定位性能要优于其他两种定位算法,定位效果较好．表1示出了三种算法定位误差比较.

表1 三种算法定位误差比较

由表1误差对比可知,本文算法的平均定位误差为1.58 m,各定位误差结果均低于BPNN和PSO-BPNN算法,其中,平均定位误差的定位精度相比PSO-BPNN算法提高了19.4%,比BPNN算法提高了32.2%,这是由于本文通过改进的人工鱼群算法优化了BP神经网络的参数,建立了更优的定位模型．在室内定位领域中,基本能够满足对误差的要求．

5 结 论

本文在室内无线定位技术的基础上,针对传统的基于BP神经网络室内定位算法存在着定位精度低和收敛速度慢的问题,利用改进的人工鱼群算法优化BP神经网络模型的权值和阈值参数,有效避免了传统BP神经网络的预测值易陷入局部最优的缺点,同时BP神经网络的学习能力也得到一定的提高,最后,将其与室内定位应用场景相结合,实验分析结果也表明,本文提出的定位算法在2 m内的误差概率为79%,平均误差为1.58 m,相对于PSO-BPNN,BPNN算法,性能均较优,定位结果较稳定．室内定位性能得到了有效的改善．