综合EGM2008和移动曲面模型的GNSS高程拟合

吴寒,吴燕苹,邓明镜

(1. 重庆交通大学 土木工程学院,重庆 400074;2. 重庆工程职业技术学院,重庆 402260)

0 引 言

随着全球卫星导航系统(GNSS)技术的快速发展,GNSS高精度定位已广泛应用于工程建设,其中GNSS高程测量由于其不同于传统水准作业方式,极大地提高了高程测量效率．但是GNSS测量的高程为大地高,并不能直接应用于工程实际需要,如何将大地高转换为工程建设所需的正常高是一个重要研究内容,其关键在于高程异常的解算[1]．

目前,高程异常解算的方法主要有物理重力法和几何拟合法[2-3],几何拟合法不深入考虑异常值造成的各种因素,统一采用数学逼近方法进行解决,比较适用于小区域或地形平坦区域的工程项目,方法简单,应用广泛,但在地形起伏较大或大范围区域,仅使用几何拟合法不能满足实际需要．随着卫星重力测量的发展,利用卫星重力资料并结合地面重力数据获得的全球重力场模型的精度和分辨率在逐步提高,特别是EGM2008模型的公布,使得利用重力场模型进行GNSS高程转换的精度和可靠性获得了大幅度提升．但是单一的拟合方法仅在一定的区域范围和地形条件下适用,为提高高程拟合的适用性、可靠性和精度,本文综合利用EGM2008模型和移动曲面模型对GNSS高程进行拟合．

1 原理与方法

1.1 整体流程

首先将高程异常分为两个部分,第一部分是由重力场模型求得的高程异常,第二部分是剩余高程异常部分,具体为

ζ=ζEGM+ζRES，

(1)

式中:ζ为总的高程异常;ζEGM为利用EGM2008模型求解所得的高程异常值;ζRES为剩余高程异常值．

选择“移去-拟合-恢复”法求解高程异常,即根据少量已知水准点,利用EGM2008模型求得对应的高程异常ζEGM,然后结合已知的高程异常ζ求得剩余高程异常值ζRES．考虑到待定点高程异常受到周边区域影响,采用以待定点为中心建立剩余高程异常值的移动曲面模型,求出待定点的剩余高程异常值ζRES,再加上对应的ζEGM即可求出待定点的高程异常[4-5]．

1.2 EGM2008重力场模型求解高程异常

EGM2008重力场模型是美国国家地理空间情报局在充分利用地面重力、卫星测高、卫星重力等多种数据的基础上研制发布的2 190次球谐系数的全球超高阶地球重力场模型,该模型的基本格网分辨率为5′,地面数据覆盖率达83.8%,该模型能够精确表达高程异常的长波项．利用EGM2008重力场模型计算高程异常的计算公式

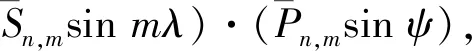
(2)

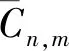
章传银等[6]对EGM2008地球重力场模型在中国大陆适用性进行分析,结果表明EGM2008模型具有很高的精度,在我国大陆的精度与全球范围内的精度相当,总体精度为20 cm,华东华中地区12 cm,华北地区达到9 cm,西部地区为24 cm．束蝉方等[7]进一步对EGM2008模型适用性分析认为将EGM2008模型和GPS结合代替低等级的水准测量是可行的,特别是对于长距离的跨障碍物的高程传递更为经济有效．荣敏等[8]利用中国854个GPS/水准点数据对EGM2008重力场模型的精度进行分析,由模型计算得到的大地水准面高与实测值之间存在明显的系统偏差．综合分析,仅使用EGM2008模型求解高程异常不能满足实际工程需要,还需对剩余的高程异常值进行处理．

1.3 剩余高程异常值的处理

在实际的工程应用中,高程拟合方法很多,当拟合区域地形平坦,范围较小时,使用二次曲面函数拟合方法就能满足一般工程需求,当地形起伏变大和拟合区域变大,二次曲面拟合函数已无法满足工程需求,而其他常用的模型如多面函数法、神经网络法等也存在计算复杂或结果随机等问题,综合考虑精度、可靠性和计算复杂性等因素,本文采用距离定权的移动曲面模型进行剩余高程异常值的处理,移动曲面模型既能很好地解决拟合面的整体性问题,抵偿部分系统偏差,同时考虑到待定点受到周边地形环境的影响情况,利用不同权重能更好地模拟待定点拟合面,适用面较广,灵活性较强,在GNSS高程转换中有着很好的优势[9-12]．具体处理方法如下．

以待定点为中心,建立剩余高程异常ζRES与对应已知点坐标(x,y)关系模型如式(3)．

ζRES=f(x,y)+ε，

(3)

式中:ε为两者的残差;f(x,y)为剩余高程异常的趋势面,常用的数学函数有曲面函数,平面函数,多项式曲线函数,在实际工程应用中,一般选择二次曲面拟合函数,其函数表达式为

f(x,y)=a0+a1x+a2y+a3x2+

a4y2+a5xy.

(4)

式(3)写成矩阵形式:

ζRES=AX+ε.

(5)

根据上述模型可知,测区已知点数量n≥6,为提高模型精度,参与模型解算的已知点可结合区域地形变化、区域大小、已知点分布和数据精度等诸多因素综合考虑．已知点与待定点的相关性一般采用距离定权方法[13-16],本文采用向径距离定权方式,即P=1/(r2+Δh2),Δh为已知点与待定点的高程差,距离r可以是选择两点之间的向量长度或两点的平面距离．

按最小二乘原理,即可求出六个参数a0、a1、a2、a3、a4、a5,由此可计算出待定点的剩余高程异常值．

1.4 几点说明

GNSS高程拟合精度除受到转换模型影响外,还受到诸多因素影响,在数据处理过程中应综合考虑．

1) 已知点的测量误差,如GNSS观测误差和水准测量误差．

2) 已知点的分布,相比曲线和曲面拟合等方法,尽管移动曲面拟合模型受点位分布的影响较小,但在实际工程中尽量保证足够的已知点分布于拟合区域范围内提高成果的可靠性．

3) 转换范围,从全国大范围来看,不同区域水准网本身也存在系统偏差,且差值各不相同,我国部分学者曾认为国家一等水准网在西部地区存在分米量级的系统偏差,有的甚至认为系统偏差超过0.5 m．因而数据处理前需对所在区域的水准网成果数据进行分析,对于采用不同水准网平差的区域或跨越不同省市地区的较大区域,可采用分区方式处理提高成果的精度和可靠性．

2 实验与分析

为验证本文方法的精度情况和适用范围,选取4个不同区域和地形环境的算例进行实验分析．

算例1:东西长约5 km,南北长约8 km,共有13个联测已知点(四等水准点),选取其中7个点作为参考点,6个点作为检核点,最高高程为326 m,最低高程为278 m,平均高程为314 m,地势平坦．

算例2:东西长约25 km,南北长约35 km,共有27个联测已知点(四等水准点),选取其中7个点作为参考点,20个点作为检核点,最高高程为508 m,最低高程为192 m,平均高程为312 m．

算例3:东西南北长约150,共有18个联测已知点(四等水准点),其平均间距为20,选取其中11个点作为参考点,7个点作为检核点,最高高程为1 501 m,最低高程为187 m,平均高程为704 m,地势起伏很大．

算例4:东西南北长约400 km,共有71个联测已知点(四等水准点),其平均间距为35 km,选取其中34个点作为参考点,37个点作为检核点,最高高程为1 548 m,最低高程为71 m,平均高程为527 m,地势起伏很大．

为了比较解算精度,以常用的二次曲面模型作比较,分别采用二次曲面模型(方法1)、移动曲面模型(方法2)、EGM2008模型和二次曲面模型组合(方法3)、EGM2008模型和移动曲面模型组合(方法4)4种方法进行计算,统计情况如表1所示．

表1中,RMSE为均方根误差,|ν|max为拟合残差绝对值最大值,从表1可知,在平坦和较小范围区域,采用4种方法的效果相当,随着拟合范围和地形起伏变大(如算例3和算例4),采用方法1和方法2已无法满足现实需求,由于EGM2008重力场模型能表达高程异常长波项,即使在大范围区域转换时也能有效地处理好高程异常系统偏差．因而,综合利用EGM2008模型的方法3和方法4表现出明显的优势．

表1 拟合精度比较mm

方法算例1RMSE|ν|max算例2RMSE|ν|max算例3RMSE|ν|max算例4RMSE|ν|max 方法12.43.314.826.3225.2364.5621.0847.7 方法22.53.415.935.9194.3208.3188.5539.8 方法33.44.66.818.535.156.066.2156.8 方法43.04.27.89.129.247.448.187.4

图1 检核点残差绝对值与四等水准限差/m

1) 方法4拟合中误差较方法3明显降低,精度改善38%．

2) 方法4和方法3在各点的拟合残差分布不一致,62%的检核点中方法4拟合残差小于方法3．

3) 方法4最大拟合残差为87.4 mm,方法3最大拟合残差为156.8 mm,按照四等几何水准的限差规范,方法4所有检核点无残差超限情况,方法3有4个点超限,方法4可靠性较好．

3 结束语

本文基于“移去-拟合-恢复”的思想,提出综合利用EGM2008模型的移动曲面模型高程拟合方法,该方法对已知点分布要求较低,计算简单,适用范围较广,可靠性高,该方法在实际工程项目尤其是大范围山区地形GNSS高程拟合中起到一定改进作用．