爬楼轮椅前腿机构的可靠度灵敏度分析

张琦 曹东兴 甘晓萌 范柳彬

摘要 针对爬楼轮椅的前腿机构，其运动精度的高低影响着爬楼轮椅整机的稳定性，运用封闭矢量法建立了前腿机构运动输入、输出模型，在同时考虑了杆件尺寸制造误差和运动副间隙误差的基础上，建立了轮腿式爬楼轮椅前腿机构输出角度可靠度、灵敏度模型，利用MATLAB编写程序对建立的数学模型进行仿真分析，得出了机构在不同运动副间隙情况下可靠度的变化规律和其在不同参数下可靠性灵敏度的变化规律，为后期提高前腿机构的运动精度设计提供理论依据。

关 键 词 爬楼轮椅前腿机构;尺寸制造误差;运动副间隙误差;可靠度;灵敏度

中圖分类号 TH789;TH112     文献标志码 A

0 引言

前腿机构作为轮腿式爬楼轮椅的前部，在轮椅上下楼梯和跨越障碍上起着至关重要的作用，前腿机构能否正常工作直接影响到爬楼轮椅的正常使用，为确保前腿机构在工作中能够按照要求达到预定的位姿，必须对其工作可靠性进行分析，由于在实际工作中，机构存在着尺寸加工误差、运动副间隙误差和输入误差等诸多因素都对机构运动精度可靠性有影响。国内外学者对此也进行了很多研究。例如文献[1-2]分析了运动副间隙对机构可靠性的影响;文献[3]对凸轮机构的运动精度仿真进行了分析;文献[4-6]探讨了曲柄滑块机构可靠性与灵敏度。目前对于机构运动精度的可靠性理论，大都研究机构运动精度模型的仿真，并考虑部分影响因素对机构可靠性灵敏度的设计。

本文同时考虑前腿机构的基本尺寸误差和运动副间隙误差两方面因素，将机构的运动精度模型与可靠性理论结合起来综合进行考虑，进而建立了运动精度可靠性及可靠性灵敏度计算的数学模型。

1 前腿机构精度问题描述

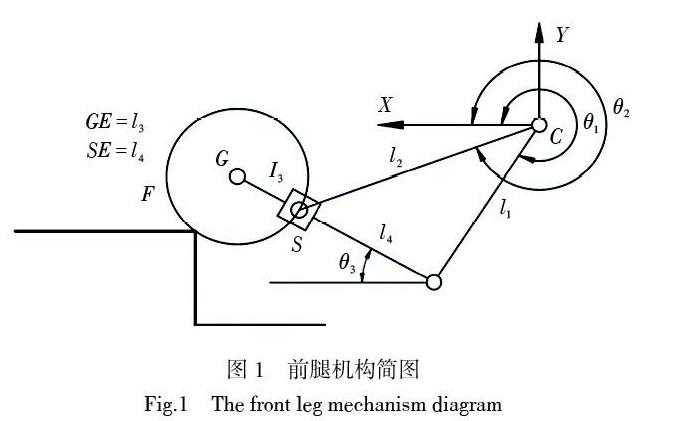
如图1所示，前腿机构通过铰链C与机架连接，杆l1和l2作为驱动杆，其中杆l1一端通过铰链C与机架连接，另一端通过铰链E与连杆l3连接;l2一端也是通过铰链C与机架连接，另一端通过铰链S与滑块连接，前腿末端装有F轮，通过铰链G与连杆L3连接，以上铰链均为转动副。

根据设计，当驱动杆l1和l2给一定的输入时，前腿机构的F轮和E轮会完成一定的动作，以辅助轮椅完成爬楼与越障等功能。但在实际工作中，在各个杆件加工误差、运动副间隙误差、输入误差等因素综合影响下，前腿机构F轮会与理想的位姿出现一定的偏差，严重影响爬楼轮椅整机的稳定性。

2 基本尺寸误差和运动副间隙对机构可靠度的影响

2.1 基本尺寸误差对机构可靠性的影响

机构的基本尺寸误差便是各杆件的几何长度误差，其主要来源于加工制造。本节便就连杆基本尺寸误差对前腿机构可靠性进行分析，并建立数学模型。

图1所示为轮腿式爬楼轮椅前腿机构简图，以输出角θ3为研究对象，即输出向量为Y = θ3，输入向量为：X = [θ1，θ2]，结构尺寸参数向量为：L = [l1，l2]，由式（1）可求得前腿机构输入和输出的函数关系

2.2 运动副原始间隙误差理论分析

运动副是由2个构件通过间隙配合而形成的活动联接，所以运动副存在着的正常运动需要一定的运动副间隙，运动副过小会使机构运动不灵活，而运动副过大会使机构的运动精度大大降低，加大运动副的冲击，增加构件的惯性应力和应变，除此之外由于机构装配不合理、生产制造有误差以及运动副长期磨损等也会造成机构运动副间隙存在误差;过大的运动副间隙会使机构产生噪声和机械效率降低，因此运动副间隙误差的研究是非常必要的;如图1所示轮腿式爬楼轮椅前腿机构存在着转动副和移动副，下面分别对其进行分析。

2.2.1 转动副间隙误差模型分析

文献[7]中提出了有效杆长的理论和误差圆内铰链的销轴中心随记分布的特点，并建立了可靠性分析的模型。由图2所示的运动副有效杆长模型知有效杆长和实际杆长之间关系为

2.2.2 移动副间隙误差模型分析

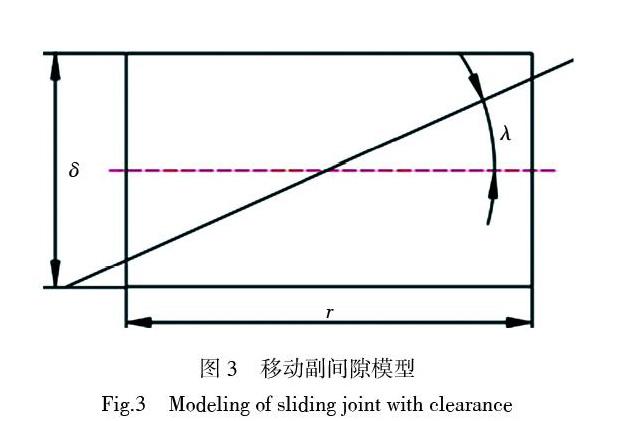
移动副约束着两杆之间的夹角，如图1所示由于其移动副间隙的存在，杆l3会绕着滑块上的一点发生微小的转动，导致机构的输出角也会发生微小的改变。故建立如图3所示的移动副间隙模型，r为滑块的长度;d为杆l3的直径大小;δ为移动副间隙大小;λ杆l3为绕滑块转动的微小偏转角，则由几何关系得

2.3 基本尺寸误差和运动副间隙误差对机构可靠性的共同影响

根据上述理论及其分析，基本尺寸误差、运动副间隙误差这2个因素都对机构运动精度产生一定的影响，下面结合基本尺寸误差分析和运动副间隙误差分析这2种理论，建立了同时考虑基本尺寸误差、运动副间隙误差这2种因素下的爬楼轮椅前腿机构运动精度可靠性及可靠性灵敏度的数学模型。其具体分析过程如下。

由式（6）可得，将考虑运动副间隙的有效杆长R替换实际杆长，则有

由式（8）可知前腿机构各个杆件考虑运动副间隙的有效长度和实际长度的均值相同，即E（Ri） = E（li），且由式（13）知在考虑移动副间隙误差情况下也不会影响输出角误差的均值，因此，爬楼轮椅前腿机构同时考虑杆件制造尺寸误差和运动副间隙误差时机构输出误差的均值和只考虑杆件制造尺寸误差的均值是一样的。但此时的方差变为

经过上述分析可知，现可计算同时考虑机构基本误差及运动副间隙误差2种因素影响下的前腿机构运动精度可靠度数学模型，另外也可对其运动精度可靠性灵敏度进行计算分析。

3 建立前腿机构运动精度可靠性数学模型

3.1 机构运动精度可靠性函数的建立

机构的运动精度是决定其能否正常工作的重要指标之一，要想使一个机构能够正常的工作，其输出的误差值必须满足该机构运动精度的要求;由于各构件的尺寸误差和运动副间隙都为随机变量且符合正态分布，因此对于前腿机构输出角度的可靠度R就是实际输出角度误差ε小于允许输出角度误差的概率，即