基于广义梯度矢量流模型图像分割算法的研究

王晨霞 于明

摘要 梯度矢量流模型（GVF）是引导主动轮廓模型形变的有效外力，但不能分割细长凹陷区域，因此提出广义梯度矢量流（GGVF）模型。GGVF模型将GVF模型中的常数系数替换为两个变化的权重函数，虽然拥有较好的细长凹陷收敛能力，但仍然在进入复杂凹陷、保护弱边缘、抵抗噪音方面存在局限性。为了解决这些问题，在GGVF模型的基础上做了3点改进：1）在构建边缘图时引入双边滤波器用于平滑噪音;2）用散度算子替代拉普拉斯算子实现更好的凹陷收敛能力;3）添加方向约束函数用于保护弱边缘。实验结果表明，该算法具有较好的性能，且相对于传统GGVF模型，召回率提高15.6%，F1值提高8.7%。

关 键 词 图像分割;主动轮廓模型;梯度矢量流模型;散度算子;双边滤波

中图分类号 TP391     文献标志码 A

主动轮廓模型，即Snake算法，自1987年被Kass等[1]提出后，就被广泛应用于图像分割领域。它将平面中曲线向目标物体的演化转化为极小化能量泛函的过程。该能量泛函可被分为内部能量和外部能量两部分，内部能量用来约束曲线的形状，外部能量则可以吸引曲线向目标边界移动。传统Snake模型中，外力来源于图像梯度，这种外力场捕捉范围很小，因此必须将初始轮廓的位置设置在目标附近时才能使其收敛到正确位置，而对于凹陷区域，这种外力场也无能为力。1998年，Xu等[2]提出梯度矢量流主动轮廓模型（GVF Snake），把图像边缘处的梯度矢量向周围进行扩散，在同质区域产生一缓慢变化的外力场，扩大捕获范围的同时在一定程度上也能抑制噪声的影响。尽管GVF Snake 模型相对传统Snake模型做了很大的改善，但是仍然存在着一些缺陷，例如难以进入细长凹陷区域，存在弱边缘泄露问题，对椒盐噪声比较敏感。因此，许多专家学者们纷纷针对梯度矢量流（GVF）模型中存在的缺陷提出改进方法[3-12]。例如，文献[3]提出广义梯度矢量流（GGVF）模型，该模型采用两个变化的权重函数分别作用于梯度矢量流模型的平滑项和保真项，使得修改后的GGVF模型可以自适应地平衡两者的扩散程度，改善了模型的细长凹陷收敛能力。文献[4]提出成分归一化的广义梯度矢量流（CNGGVF）模型，该模型用成分归一化的方法替代传统矢量归一化的方法，在GGVF模型的基础上进一步改善了模型深度凹陷收敛的能力。文献[7]提出导向滤波梯度矢量流（GFGVF）模型，该模型通过改写边缘图和权重函数，进一步改善了模型的边缘保护能力。

在本文中，提出一个基于传统GGVF的改进模型，旨在改善模型的整体功能，包括噪声鲁棒性、深度凹陷收敛性能和弱边缘保护性能。本文的主要贡献包括以下几个方面。

1）引入双边滤波器用以构建新的边缘图。双边滤波可以同时具有保持边缘、降噪平滑的作用.这在一定程度上解决了边缘泄漏弱的问题。因此，双边滤波具有更好的滤波效果。

2）用散度算子去替代拉普拉斯算子。这样可以改变梯度矢量从边缘区域到同质区域的扩散方式，继而可以改善新模型对凹陷区域的收敛性能。

3）添加方向约束函数。这样可以使得边缘处的扩散是沿垂直于梯度的方向进行而不是跨越边缘方向，因此弱边缘可以得以有效保留。

1 Snake，GVF和GGVF模型

1.1 Snake模型

1987年Kass等[1]首次提出Snake模型，它实际上是描述一个连续的闭合曲线[c（s）=（x（s），y（s））]，[s∈[0，1]]，在图像空间域中的演化过程可以用最小化以下能量函数来表示：

1.2 GVF Snake模型

为了克服传统Snake模型的两个关键性局限，Xu等[2]提出GVF模型，用来替代传统Snake模型的外力，它可以表示为一个向量场[v（x，y）=[u（x，y），v（x，y）]]，通过极小化如下能量泛函得到：

GGVF模型具有自适应扩散的能力，在式（7）中，第一项为平滑项，主要作用在同质区域，具有各向同性的平滑效果。第二项為数据项，主要作用在边缘区域附近，使得到的力场尽可能接近图像梯度矢量。参数[k]的作用与GVF模型中[μ]的作用类似。

2 新模型的提出

2.1 引入双边滤波器构造新的边缘图

在实际应用中，为了减少噪音的干扰，往往会对原图进行滤波处理。传统的滤波器，如高斯滤波会在平滑噪音的同时将边缘信息也模糊掉。而文献[13]提出的双边滤波器通过结合距离差异权重和灰度值差异权重很好地解决了这一问题，式（10）、式（11）给出了双边滤波的操作过程，[Iq]为输入图像，[Ibf]为滤波后图像。

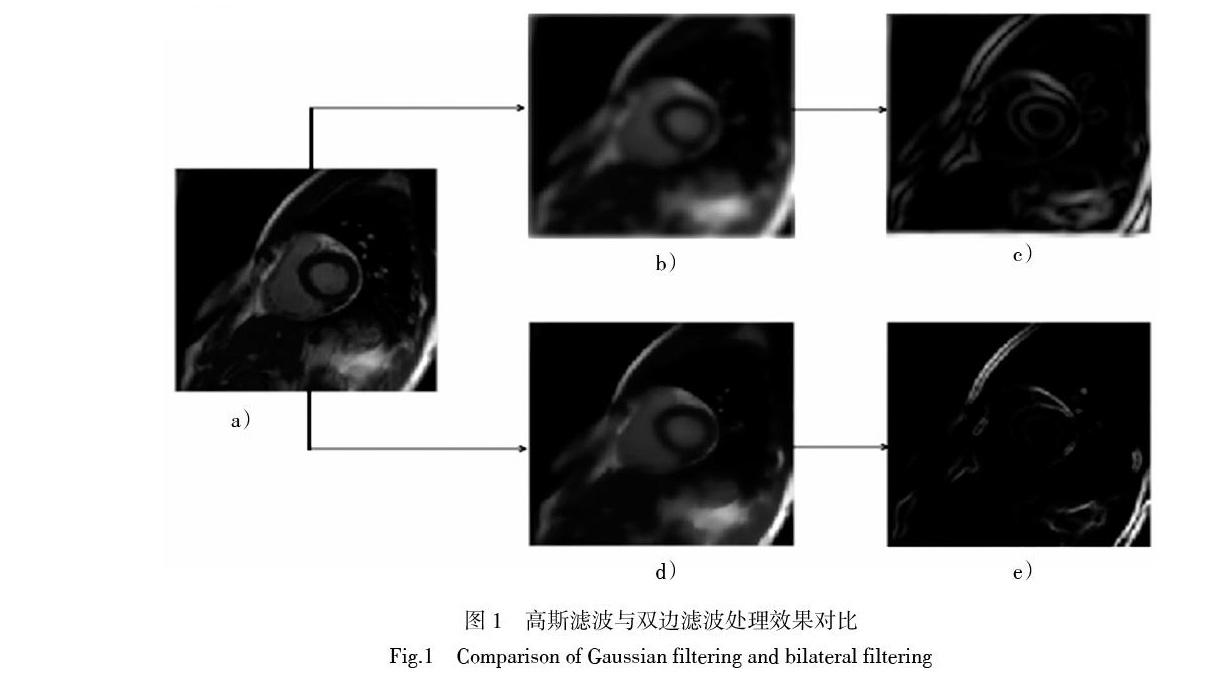
式中：[σs]为空域高斯函数的标准差;[σr]为值域高斯函数的标准差。在同质区域，[Ip-Iq]的值变化很小，对应的值域权重接近于1，此时空域权重起主要作用，相当于直接对此区域进行高斯模糊。在边缘区域，[Ip-Iq]会有较大的差异，此时值域权重会下降，从而导致此处整个核函数的分布的下降，而保持了边缘的细节信息。在此基础上，新的边缘图可以通过[e（x，y）=    I（x，y）bf]得到。图1给出了分别经过高斯滤波和双边滤波处理的效果，其中图1a）为输入图像，图1 b）和d）分别为经过高斯滤波和双边滤波处理后的输出图像， 图1c）和e）分别为对应 图1b）和d）得到的边缘图。如图1所示，输入图像经过高斯滤波处理后，噪音可以被平滑，但是边缘图中的边缘信息也被模糊了。然而在经过双边滤波器处理之后，边缘图中的边缘仍然清晰可辨。

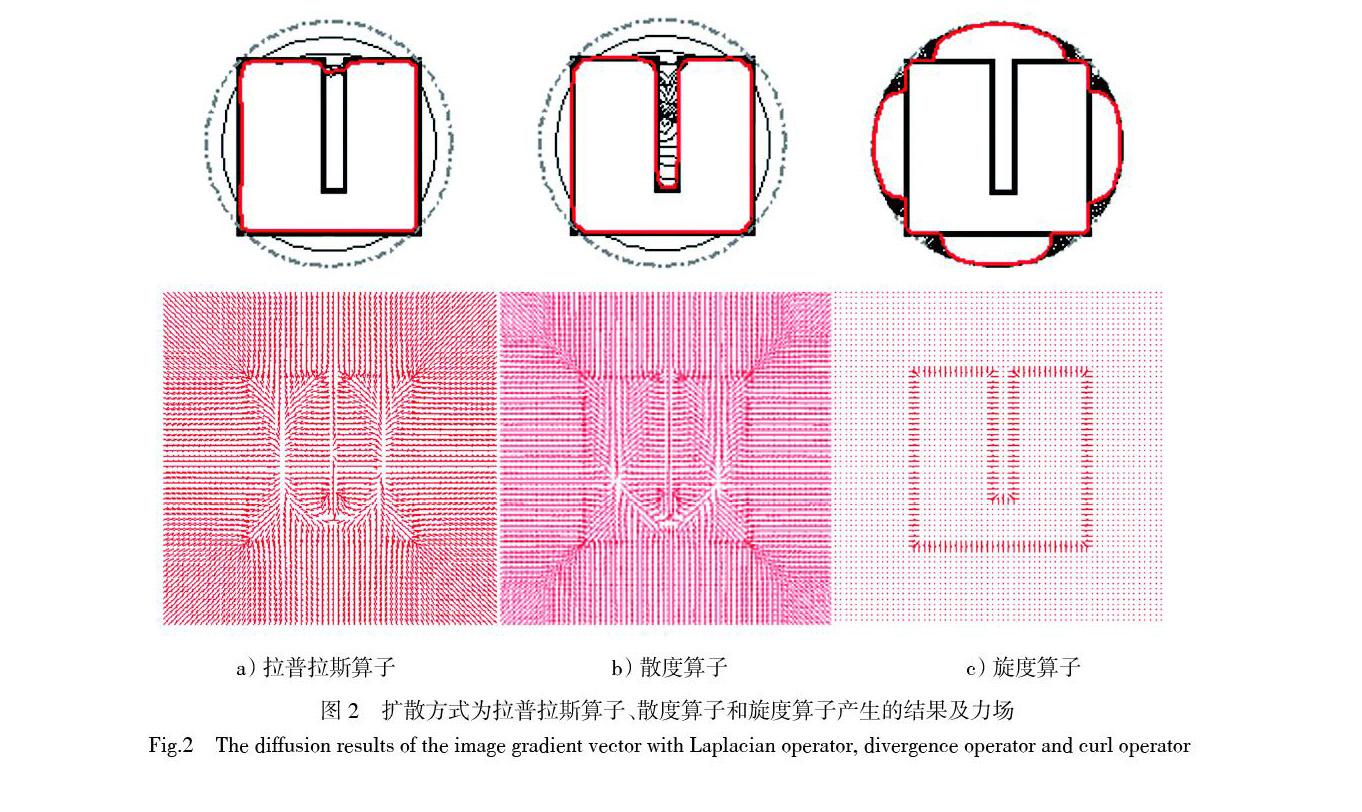
2.2 用散度算子替代拉普拉斯算子

由第1.2节分析可知，GVF模型中边缘梯度矢量的扩散主要依赖于平滑项中的拉普拉斯算子。根据亥姆霍兹定理，任意矢量场可以分解为无散量和无旋量。因此，拉普拉斯算子的能量函数可以被拆分为

算法性能的主观评价具有一定的局限性，为了进一步评估算法分割的准确性，本文采用精确率（Precision）、召回率（Recall）和F1值对实验结果进行客观评价，分别定义为

式中：[Mseg]和[Gseg]分别表示算法分割得到的对象區域和真实轮廓包含的对象区域。当上述3种度量均为1时，表示由算法得到的对象区域与标准对象区域完全重合，更详细的信息可见文献[16-18]。在表1中，给出GVF、GGVF、NGVF、CNGGVF、GFGVF和新模型分割5副医学图像得到结果的定量评价值，并计算出每个模型关于5副医学图像分割结果的平均指标。仔细观察表中数据，可以得到以下结论：1）在所有医学图像中，新模型具有最高的F1值;2）最后一列的平均评价指标表明新模型具有最高的召回率和F1值;3）与传统GGVF模型相比，新模型增加了约15.6%的召回率和8.7%的F1值。因此，从客观评价角度分析，本文提出的方法能够更准确地分割医学图像中的目标区域。

4 结语

基于传统GGVF模型在进入复杂凹陷，保护弱边缘，抵抗噪音方面存在的局限，提出了一种新的主动轮廓外力，它结合使用了双边滤波器，散度算子和方向约束函数。为了评价所提出模型的性能，将其与GVF、GGVF、NGVF、CNGGVF和GFGVF模型进行了比较。人工合成图像的实验结果表明，该模型在噪声鲁棒性，深度凹陷收敛性能和弱边缘保护方面优于传统模型。另外，新模型还被用于医学图像分割，并且定量和定性的实验结果显示其相对于其他传统模型具有更准确的分割结果。

参考文献：

[1]    KASS M，WITKIN A，TERZOPOULOS D. Snakes：Active contour models[J]. International Journal of Computer Vision，1988，1（4）：321-331.

[2]    XU C，PRINCE J L. Gradient vector flow：a new external force for snakes[C]// IEEE Computer Society Conference on Computer Vision and Pattern Recognition（CVPR）. San Juan，Puerto Rico，1997：66-71.

[3]    XU C Y，PRINCE J L. Generalized gradient vector flow external forces for active contours[J]. Signal Processing，1998，71（2）：131-139.

[4]    QIN L M，ZHU C，ZHAO Y，et al. Generalized gradient vector flow for snakes：new observations，analysis，and improvement[J]. IEEE Transactions on Circuits and Systems for Video Technology，2013，23（5）：883-897.

[5]    祝世平，高瑞东. 基于自适应扩散梯度矢量流的图像分割算法[J]. 光电子·激光，2015（12）：2409-2416.

[6]    张静林，高红，马宝英. 一种改进的梯度矢量流Snake侧脑室分割算法[J]. 中国医学物理学杂志，2015，32（5）：711-716.

[7]    ZHAO F，ZHAO J，ZHAO W D，et al. Guide filter-based gradient vector flow module for infrared image segmentation[J]. Applied Optics，2015，54（33）：9809-9817.

[8]    ANANTH C，KARTHIKA S，SINGH S. Graph Cutting Tumor Images[J]. Social Science Electronic Publishing，2017，4（3）：309-314.

[9]    邹北骥，张思剑，朱承璋. 彩色眼底图像视盘自动定位与分割[J]. 光学 精密工程，2015，23（4）：1187-1195.

[10]  REN D W，ZUO W，ZHAO X F，et al. Fast gradient vector flow computation based on augmented Lagrangian method[J]. Pattern Recognition Letters，2013，34（2）：219-225.

[11]  NAKHMANI A，TANNENBAUM A. Self-crossing detection and location for parametric active contours[J]. IEEE Transactions on Image Processing，2012，21（7）：3150-3156.

[12]  GUO Q，SUN S F，REN X H，et al. Frequency-tuned active contour model[J]. Neurocomputing，2018，275：2307-2316.

[13]  TOMASI C，MANDUCHI R. Bilateral filtering for gray and color images[C]//Sixth International Conference on Computer Vision （IEEE Cat. No. 98CH36271），Bombay，India. Narosa Publishing House，1998：839-846.

[14]  LI C M，LIU J D，FOX M D. Segmentation of external force field for automatic initialization and splitting of snakes[J]. Pattern Recognition，2005，38（11）：1947-1960.

[15]  LI Q，DENG T Q，XIE W. Active contours driven by divergence of gradient vector flow[J]. Signal Processing，2016，120（3）：185-199.

[16]  FERGANI K，LUI D，SCHARFENBERGER C，et al. Hybrid structural and texture distinctiveness vector field convolution for region segmentation[J]. Computer Vision and Image Understanding，2014，125：85-96.

[17]  ESTRADA F J，JEPSON A D. Benchmarking image segmentation algorithms[J]. International Journal of Computer Vision，2009，85（2）：167-181.

[18]  ZHU S P，BU X Y，ZHOU Q. A novel edge preserving active contour model using guided filter and harmonic surface function for infrared image segmentation[J]. IEEE Access，2018，6：5493-5510.

[責任编辑 田 丰]