探讨新课标下高中数学的最值问题

杨文娟

(江苏省徐州市郑集高级中学 221100)

高中数学新课标比较重视学习者能力的提高，包括发现、提出、分析和解决问题的能力，因此在讲解最值问题时，应在新课标的框架下，结合具体例题，为学习者讲解求解对折的方法与技巧，提高其解答该种数学题型的能力，不断提高学生的数学学习成绩.

一、回归教材，夯实基础

新课标下，提高学习者解答高中数学最值问题的能力需牢固掌握基础知识，以灵活应用，提高解题正确率，因此授课中，应引导学习者回归教材，脚踏实地，准确记忆相关数学公式，并加深理解.一方面，为学习者深入细致的讲解与最值相关的数学知识点，如函数单调性、三角函数的有界性、以及均值不等式知识，使其认识到在讨论最值问题时应注重定义域，以及均值不等式等号成立的条件.另一方面，为使学习者确实夯实基础，应注重为学习者讲解基础题型，使其认真把握解答最值问题的细节，充分挖掘隐含条件，养成良好的解题习惯.

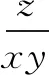
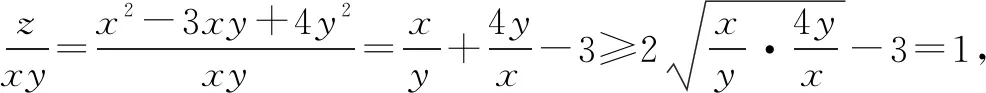
该题目涉及的知识点较多，包括基本不等式以及二次函数知识，从中也可以看出夯实基础的重要性，因此，授课中引导学习者不要好高骛远，搞清楚基础知识的来龙去脉，为其灵活、正确应用奠定基础.

二、传授方法，拓展思维

最值问题题型复杂多变，解题方法多种多样.针对部分题型，只有选择正确的方法，才能迅速高效的得到正确答案，因此授课中应注重为学习者讲解解题方法，积极拓展其解题思维.一方面，求解最值问题常用的方法有：函数法、导数法，以及均值不等式法，授课中应围绕具体例题，为学习者讲解这些方法的具体应用，并讲解这些方法的应用技巧，不断提高应用水平.另一方面，结合以往授课经验，注重创设较为新颖的问题情境，不断拓展学习者的解题思维，给其以后解答类似问题，带来良好启发.

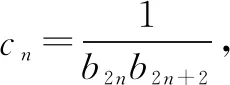
通过该题目的讲解，进一步巩固了学习者已学的数列裂项求和知识，给求解数列最值问题指明了思路，即，在解答数列最大值最小值问题时，应充分理解数列与函数之间的关系，借助函数的单调性求解.

三、加强训练，提高技能

求解高中数学最值问题具有较强的技巧性，对学习者解题的灵活性要求较高，因此为提高学习者的解题能力，应做好日常的解题训练，使学习者在训练中知识得以巩固，思维的灵活性可以提高.具体可从以下两个方面进行突破：一方面，做好训练课时安排，结合具体题型，用心筛选训练试题，积极开展专题训练活动.在训练中要求学习者，独立思考，认真回顾所学，积极谨慎地解答，提高解题技能.另一方面，鼓励学习者反思解题过程，思考推理是否严密，做好解题过程优化.同时，鼓励其进行一题多解，即，结合所学的解题方法，看能否找到更为简便的解题途径，促进最值问题解题技能的提高.

例3已知函数f(x)=-x3+ax2-4在x=2处取得极值，若m，n∈[-1，1]，则f(m)+f′(n)的最小值是____.

认真审题可知，该函数为一元三次函数，因此在求解最值时，需首先考虑采用导数法求解.根据所学的导数知识，分别求解出f(m)、f′(n)的最小值，然后使两者相加即可.由函数在x=2取得极值不难求出a=3.则f′(x)=-3x2+6x，令f′(x)=0，可知x=0或x=2.当x<0时，f′(x)<0；当00；当x>2时，f′(x)<0.因此，m∈[-1，1]时，f(m)的最小值为f(0)=-4.又因为f′(n)=-3n2+6n，在[-1，1]上单调递增，因此，f′(n)的最小值为f′(-1)=-9.综上可知，f(m)+f′(n)的最小值=-4-9=-13.

通过该题目的训练，能很好地提高学习者解答最值问题的灵活性，能够根据题设条件，认真联系所学，及时寻找解题突破口，避免在解题中走弯路，实现解题效率的提高.

综上所述，新课标下，为提高高中数学最值问题的教学质量，提高学习者解答该题型的能力，授课中既要引导学习者重视教材内容，切实夯实基础知识，又要总结与传授相关的解题方法，使学习者在解题中少走弯路.同时，注重优选经典题型，对学习者进行专题训练，使其在训练中灵活应用所学，实现解题技能的提升.