利用对称轴确定磁偏转圆心
亢小宁
(陕西省榆林府谷中学 719400)
案例(2013新课标Ⅰ卷)如图1所示,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外.一电荷量为q(q>0),质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为R/2.已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( ).
A.qBR/2mB.qBR/mC. 3qBR/2mD.2qBR/m
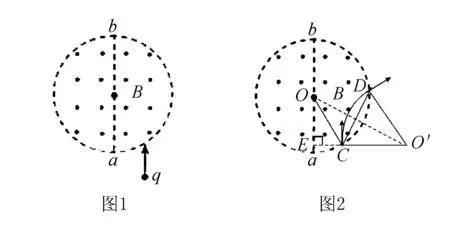
解析粒子从C点射入,过C作速度方向的垂线CE,再过磁场圆圆心作一条直线与垂线CE成30°,此时交点O′为粒子轨迹圆的圆心,然后以O′为圆心画轨迹,如图2所示,可以看出OO′为轨迹对称轴,把圆心角平分,圆心角等于速度偏转角,即∠CO′D=60°,对称轴平分圆心角,又CE=R/2,则∠COE=30°,∠COO′ =∠CO′O= 30°,CO′ =CO,即r=R.再根据洛仑兹力提供向心力有,qvB=mv2/R解得v=qBR/m,所以B选项正确.
常见的此类题还有不少题目,均可尝试此解法.
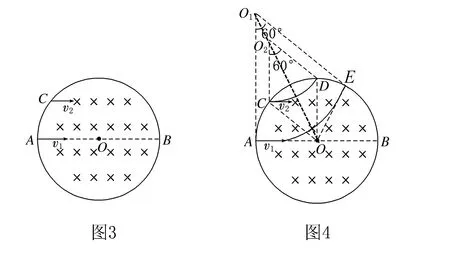
活学活用1(2018·资阳模拟)如图3所示,半径为R的圆形区域内存在垂直于纸面向里的匀强磁场,一带正电粒子以速度v1从A点沿直径AOB方向射入磁场,经过时间t1射出磁场.另一相同的带电粒子以速度v2从距离直径AOB的距离为R/2的C点,平行于直径AOB方向射入磁场,经过时间t2射出磁场.两种情况下,粒子射出磁场时的速度方向与初速度方向间的夹角均为60°.不计粒子受到的重力,则( ).
C.t1=t2D.t1>t2
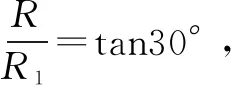
活学活用2如图5所示,圆形区域内有垂直于纸面的匀强磁场(图中未画出),O为圆心,P为边界上的一点.相同的带电粒子a、b(不计重力)先后从P点射入磁场,粒子a正对圆心射入,速度方向改变60°后离开磁场,粒子b射入磁场时的速度方向与粒子a射入时的速度方向成60°角,已知它们离开磁场的位置相同.下列说法正确的是( ).
A.a、b两粒子的速度大小之比va∶vb=1∶2
B.a、b两粒子在磁场中运动的时间之比ta∶tb=1∶3
C.a、b两粒子在磁场中运动的半径之比ra∶rb=1∶2
D.a、b两粒子在磁场中运动的轨迹长度之比sa∶sb=2∶3
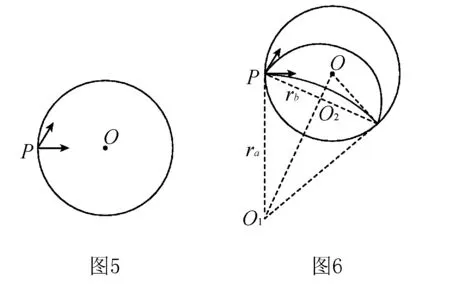
解析粒子a从P点射入,过P作速度方向的垂线PM,再过磁场圆圆心作一条直线与垂线PM成30°,此时交点O1为粒子轨迹圆的圆心,然后以O1为圆心画轨迹,可以看出OO1为轨迹对称轴,把圆心角平分,圆心角等于速度偏转角,对称轴平分圆心角,则∠PO1O=30°;粒子b从P点射入,过P作速度方向的垂线PN,再过磁场圆圆心作一条直线与垂线PN成30°,此时交点O2为粒子轨迹圆的圆心,然后以O2为圆心画轨迹,带电粒子a、b在磁场中运动的轨迹,如图6所示,根据几何关系可知,a、b两粒子运动的轨迹半径之比ra∶rb=2∶1,选项C错误;由r=mv/Bq可得,a、b两粒子的速度大小之比va∶vb=2∶1,选项A错误;a、b两粒子在磁场中运动的轨迹对应的圆心角之比为1∶3,根据T=2πm/Bq,t=θT/2π可得,a、b两粒子在磁场中运动的时间之比ta∶tb=1∶3,选项B正确;根据运动的轨迹长度s=vt可得,a、b两粒子在磁场中运动的轨迹长度之比sa∶sb=2∶3,选项D正确.
“带电粒子在磁场中的运动”是高中物理的重难点,其难度主要在于“几何关系”的确定,包括圆心、角度、长度等.上述类型问题在参考资料的讲解中,对“几何关系”的说明一带而过,不能帮助学生准确定圆心突破难点.通过以上分析可以看到,“对称轴法”的构建可以帮助学生迅速准确的找到轨迹圆圆心,使几何图形规范,便于观察分析,快速找到边角关系,进而顺利解决问题.

