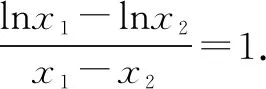极值偏移构造函数 对数平均更显威力
廖国达
(广东省梅县东山中学 514017)
在函数、导数、不等式交汇处命题,毫无疑问,这是历年高考题中的必选动作,此类问题有恒成立问题、存在性问题、零点问题、极值问题、证明不等式等问题,解决这类问题的常见的方法有:数形结合、分类讨论、分类参数、函数隐性零点以及等价转化等数学方法,在此特别值得关注的是构造模型函数或用对数平均不等式解决极值偏移问题的方法,相信你阅读后一定能对极值点偏移问题有全面的认识,此后再见必能从容不迫、游刃有余.
一、问题呈现
已知f(x)=ex-ax(x∈R)(e为自然对数的底数).
(1)讨论f(x)的单调性;
(2)若f(x)有两个零点x1,x2,求a的取值范围;
(3)在(1)的条件下,求证:x1+x2<2lna;
(4)在(1)的条件下,求证:x1·x2<(lna)2(a>e)
(5)问在(1)的条件下,求证:x1+x2>2.
二、初告战捷——求导、零点存在定理
第一二问题符合平时的考题入口宽、易上手,不难得出答案:第一问求出函数的导数,通过讨论a的范围,分别令f′(x)>0求得x的范围,可得函数f(x)的增区间,f′(x)<0,求得x的范围,可得函数f(x)的减区间;第二问由(1)知,当a≤0时,f(x)在R上为增函数,f(x)不合题意;当a>0时,f(x) 的递增区间为(lna,+∞),递减区间为(-∞,lna),只需f(x)min=f(lna)<0,即可解得a的取值范围为a>e.
三、程氏三斧——极值点偏移解题套路
第三问由所证结论可知这是f(x)的极值点偏移问题,由下面三步来完成:
第一步:由(2),当a>e时,若f(x)有两个零点x1,x2,且f(x)在(lna,+∞)上递增,(-∞,lna)上递减,依题意,f(x1)=f(x2)=0,不妨设x1 第二步:构造函数F(x)=f(x)-f(2x0-x)(x 则F(x) 的递增区间为(-∞,x0),F(x) 注2:复合函数求导:f(2x0-x)的导数为-f′(2x0-x). 第三步:f(x2)=f(x1) 第四问由所证结论可知这是f(x)的极值点偏移问题,由下面三步来完成: 第一步:由(2),当a>e时,若f(x)有两个零点x1,x2,且f(x)在(lna,+∞)上递增,(-∞,lna)上递减,依题意,f(x1)=f(x2)=0,不妨设x1 加强问题:问题(4)加强为在(2)的条件下,求证:x1·x2<1<(lna)2(a>e). 第一步:由(2),当a>e时,若f(x)有两个零点x1,x2,且f(x)在(lna,+∞)上递增,(-∞,lna)上递减,依题意,f(x1)=f(x2)=0,不妨设x1 第一步:g(x)在(-∞,0)上单调减,在(0,1)上单调减,在(1,+∞)上递增,g(x)的正负符号与x的符号相同,x→-∞,g(x)→0-; x→0-,g(x)→-∞;x→0+,g(x)→+∞;x→+∞,g(x)→+∞; g(x1)=g(x2)=a,不妨设0 移动平台上机械手的三维模型如图1所示,它是所有关节均为旋转副的五自由度关节机械臂。按照修补程序中手端的动作顺序,关节1、2、3的运动保证手端准确定位,关节4、5的运动确定手端的俯仰角度,完成修补前准备工作。 再次回到题设条件:f(x)=0⟺ex=ax(a>e)⟺x=lna+lnx⟺x-lnx=lna. 记函数h(x)=x-lnx,则有h(x1)=h(x2)=lna.接下来我们选取函数h(x)再解两问. 思路分析f(x)=0⟺ex=ax(a>e)⟺x=lna+lnx(a>e).x1=lna+lnx1,x2=lna+lnx2, 最后附一道对称型偏移问题,有兴趣的读者可以尝试解题:若关于x的方程xlnx=m有两个不相等实数解x1,x2.四、见山非山——套路通法受阻
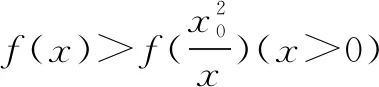
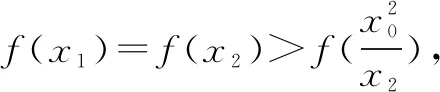

五、山重水复——加强不等式引路
六、秘境探幽——重新构造函数
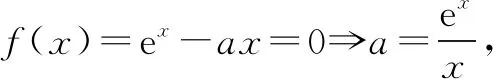
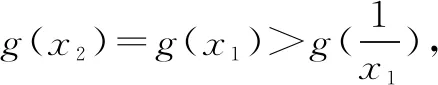
七、顺势而上——柳暗花明显思路
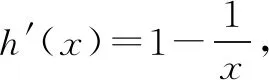
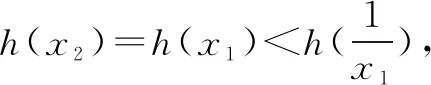
八、拾级而上——对数平均简洁至美