堆芯补水箱地震易损性分析

鄂万江，玉 宇，王鹏飞，彭礼韬

(1.华北电力大学 核科学与工程学院，北京 102206；2.非能动核能安全技术北京市重点实验室，北京 102206)

日本福岛核电站事故之后，人们意识到外部事件对核电站潜在的巨大威胁，通过各种方法来提高核电站抵御外部灾害的能力。地震作为主要的外部事件之一，具有极大的不确定性和随机性，通常采用抗震裕度评价(SMA)和地震概率安全评价(PSA)方法进行核电厂的地震安全评价[1]。对构筑物、设备进行易损性分析是其中的一个重要步骤。堆芯补水箱(CMT)是AP1000核电站非能动堆芯冷却系统的重要组成设备，通过有限元软件ANSYS建立其三维有限元模型，采用模态分析方法以获得CMT正常运行工况下的自振频率和振型，作为动力时程分析的基础，采用时程分析法可较为真实准确地模拟其地震响应。通过设备易损性计算模型，计算CMT的相关易损性参数。由于地震易损性分析中涉及大量关于结构、设备以及分析方法的相关变量，本文通过对易损性分析过程中所涉及的变量在分析过程中可能产生的误差即随机性对数标准差βR和不确定性对数标准差βU进行敏感性分析，以获得关键参量误差对地震易损性以及高置信度低失效概率(HCLPF)值的影响。

1 易损性分析方法

1.1 易损性分析数学模型

如果给定了结构或设备在地震下的失效模式，那么其地震易损性定义为在给定的地震动参数(峰值地面加速度或不同频率下的谱加速度)下的条件失效概率[2]。核电站设备的易损性模型常使用双对数正态分布，这种分布很好地模拟了结构和部件的真实易损性分布，且在数学上能方便地分析其概率分布[1]。当确定了描述抗震能力的随机性抗震能力中值Am和对数标准差βR，即可计算在不同运动水平条件下的失效概率。

对于特定失效方式，其地面加速度容量可由中值地面加速度容量Am和两个随机变量[3]表示：

A=AmeReU

(1)

式中：A为构件的抗震能力，m/s2；eR和eU为中值为1的随机变量，分别表示中值所固有的随机性和不确定性。

在该模型中，假设eR和eU服从对数正态分布，其对数标准差分别为βR和βU。在每个加速度处，f将被表示成为一个主观概率密度函数，在给定峰值加速度a条件下，构件的条件失效概率f0[3]为：

(2)

式中：Q为主观概率(置信度)，通过该值可得到1组易损性曲线；φ为标准正态累积分布函数，φ-1为正态累计分布函数的反函数。

均值易损性曲线通过组合变量标准差βC来描述，将βC代入上式即可获得设备的均值易损性分布，其中[3]：

(3)

高置信度低失效概率(HCLPF)值是指在具有95%置信度的易损性曲线上，对应具有5%失效概率的抗震能力值[2]，其值越高，表明设备抗震能力越强，计算式[3]为：

HCLPF=Ame-1.645(βR+βU)

(4)

1.2 设备易损性计算方法

设备易损性评价的目的是要给出设备在特定失效模式下的中值抗震能力、随机性、不确定性以及设备的HCLPF能力[4]。引入安全因子作为中间参数，能方便计算易损性参数，其定义为结构实际抗震能力与其在安全停堆地震下的响应的比值。对于设备，其安全因子F由容量因子FC、结构响应因子FSR、设备响应因子FER复合而成，其表达式[5]为：

F=FCFSRFER

(5)

容量因子FC表征设备不再执行其抗震设计级别下预期功能时的加速度与设计地震水平加速度的比值，设备的FC可通过下式[5]计算：

FC=FμFS

(6)

式中：Fμ为非弹性能量吸收因子(延性因子)，为延性比μ的函数，延性因子描述了在地震的作用下设备进入塑性会吸收一部分能量从而保持其功能的能力[6]；FS为极限强度(或失去功能对应的强度)与在SSE作用下的应力的比值。计算FS时，非地震部分的应力要扣除，表达式[5]为：

(7)

式中：S为特定失效模式下结构单元的强度，Pa；PN为正常运行载荷(自重载荷、运行温度等)引起的应力，Pa；PT为总应力(即SSE、正常运行载荷作用下应力总和)，Pa。

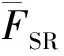
(8)

(9)

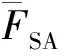
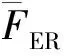
(10)

(11)

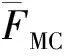
抗震能力中值Am、中值安全因子Fm和ASSE之间的关系[5]如下：

Am=FmASSE

(12)

2 CMT动力学分析

2.1 模态分析

AP1000核电站CMT是带有半球形上下封头的立式圆柱形碳钢容器并且内衬为不锈钢。在正常运行期间，CMT完全充满硼水，其压力通过冷管段压力平衡管线维持与反应堆冷却剂系统(RCS)相同的压力，为15.9MPa，由于CMT无保温或加热功能，因此，硼水的温度与安全壳环境温度相同[7]。图1为CMT几何模型及1/2结构有限元模型。

图1 CMT几何模型及1/2结构有限元模型Fig.1 Geometric model and 1/2 structural finite element model of CMT

由于CMT中完全充满硼水，采用附加质量法来模拟水对箱体的作用。在ANSYS中对CMT进行模态分析，以获得其结构的固有频率和主振型，了解结构的振动特性，通过扩展提取CMT前6阶模态。表1列出了前6阶模态振型对应的频率。从表1可发现，1阶频率为其固有频率。

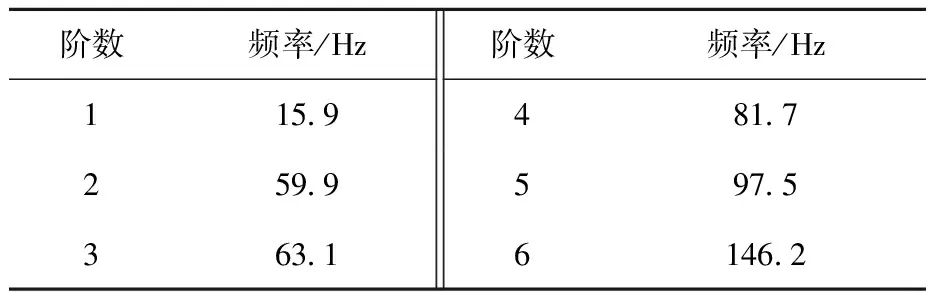
表1 CMT前6阶模态振型对应的频率Table 1 Frequencies corresponding to the first six modes of CMT

2.2 动力时程分析

结构在地震载荷作用下的响应有3种分析方法：等效静力法、反应谱法和时程法[8]。等效静力方法计算简便，计算速度较快，但忽略了结构自身的振动特性；反应谱法则是基于模态分析的结果，采用折算加速度作为地震力的特征进行计算，具备一般性，较为合理；与反应谱法相比，时程法采用逐步积分的方法对动力方程直接积分，可求解结构在地震过程中任一瞬时的位移、速度、加速度和应力等，虽然计算时间相对较长，但能真实准确模拟地震响应，计算结果更准确。

对设备的地震时程分析一般是先进行系统的抗震分析，得到主要楼层的反应谱和加速度谱，然后将楼层反应谱作为楼层震动的输入条件，再对所在楼层的设备进行抗震分析。图2a为CMT所在位置楼层谱，根据楼层谱生成时间历程曲线，如图2b所示。随后在ANSYS中通过动力时程分析，获得其在地震中所受的最大应力。

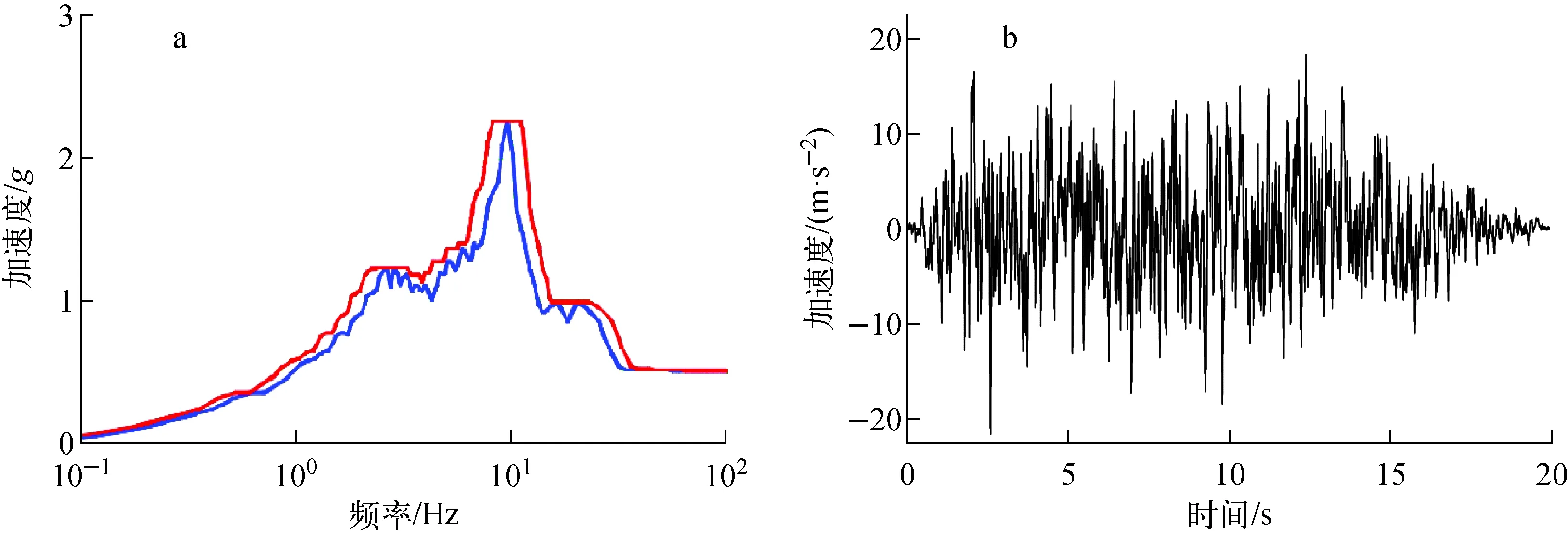
图2 楼层谱(a)和加速度时程(b)Fig.2 Floor spectrum (a) and acceleration time history (b)

3 易损性分析计算

3.1 失效模式

在核电厂中，安全相关设备的失效意味着不能执行其安全功能。设备的失效模式可分为3种：弹性功能失效、脆性失效和韧性失效[9]。弹性功能失效是指当构件受力低于屈服点时，预期功能的丧失，如容器壁和设备支撑处的弹性屈曲、风机叶片的过度变形和电气设备中发生颤振和跳闸等；脆性失效是指有很少或没有系统非弹性能量吸收能力的失效模式，如锚固螺栓失效、设备支撑焊接失效和安全销失效等，组件以脆性模式失效时的强度可用材料的极限强度来计算；韧性失效模式是指在失效时，结构系统能通过非弹性损耗，吸收大量的能量，组件以韧性模式失效时的强度用材料拉伸负荷的有效屈服强度计算[10]。

CMT上封头顶部为进口接管孔，接冷管段的压力平衡管线，下封头底部为出口接管，与压力管线容器直接注入管线相连。在容器底部安装着将容器静载荷及动载荷传递至地基处的8个支撑柱，均布于下封头上；每个支撑柱由支撑柱及底板组成，支撑柱焊接在下封头上[11]。CMT失效，即当需向RCS提供流量时，CMT无法提供足够补水。图3为地震情况下CMT支撑柱所受最大应力强度分布云图，从图3可看出，造成CMT失效的大应力强度主要分布在支撑柱与箱体焊接处，因此其失效可考虑为脆性失效，地震条件下楼层晃动，CMT支撑柱与箱体焊接处断裂，CMT侧翻，CMT出口接管处发生变形或破裂，无法及时向RCS提供足够流量。

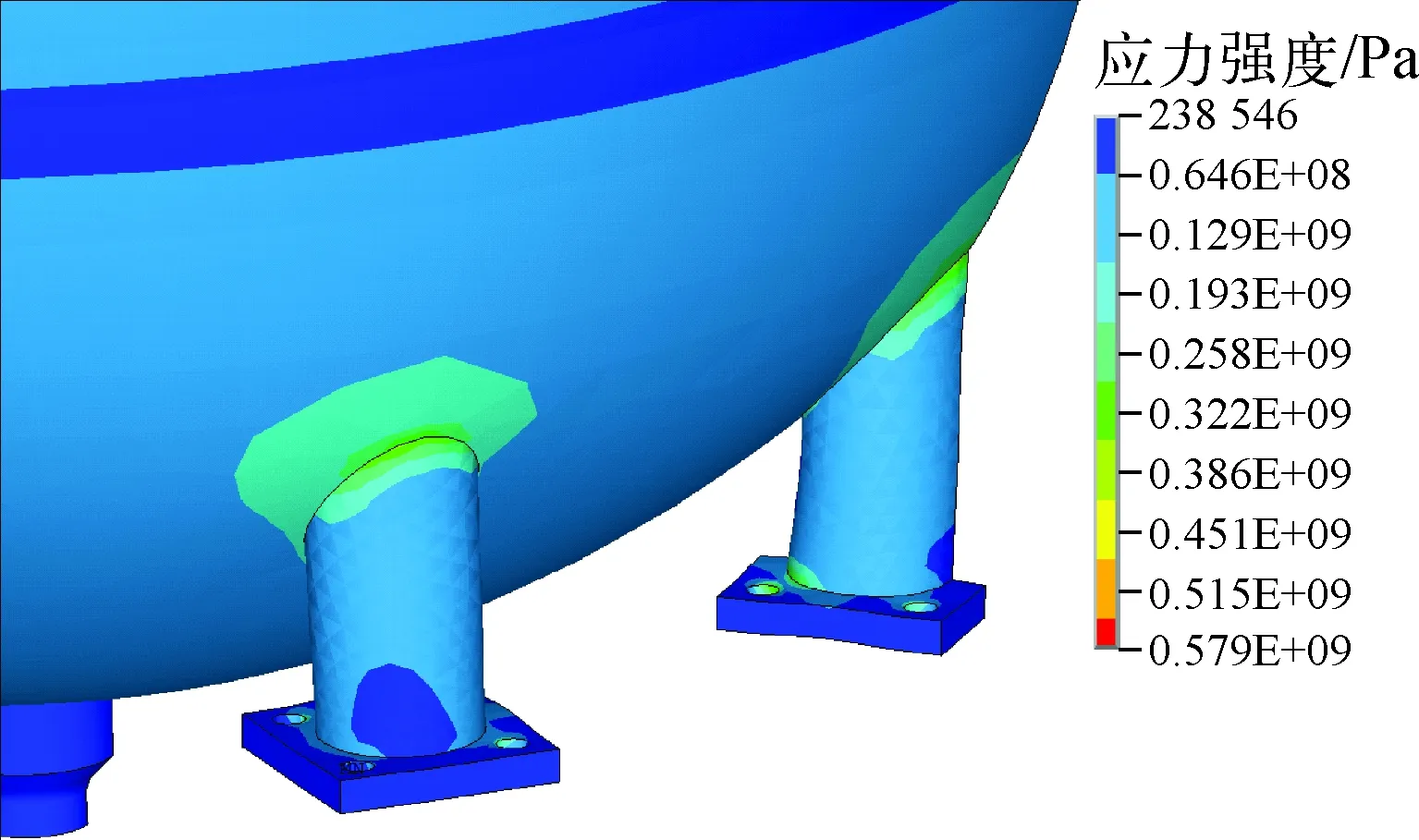
图3 CMT支撑柱应力强度分布云图Fig.3 Cloud map of stress strength distribution of CMT supporting column

3.2 容量因子FC

对于脆性和功能失效模式，中值延性因子假定为1.00，且随机性和不确定性对数标准差为0[7]。

综上，可得出CMT的FC=5.64、βU=0.11。

3.3 设备响应因子FER

在设备的易损性分析过程中，如果使用恰当的分析流程和准确的材料特性来分析设备的临界失效模式，那么中值量化方法因子FQM考虑为1.00，不确定性为0。CMT建模过程中使用真实尺寸及材料特性，则FQM= 1.00、βU= 0。

设备模型因子FM可用其模态频率和振型的不确定性来评估[10]。动力学分析应尽可能采用能准确表示设备强度、质量特性以及边界条件的模型。在建模过程中，对CMT的人孔盖位置进行了部分简化，则FM考虑为0.86。模态振型变化引起的βUM为0.05～0.15[10]，由于CMT结构较为简单，不确定性取下限值，即βUM=0.05。对于模态频率引起的不确定性βUf可由频率变化引起的反应谱值变化进行计算。频率变化范围通过下式[13]计算：

(13)

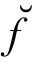
(14)

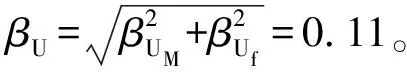
CMT结构较为简单，通过模态分析可知，其模态为单模简单振型。因此，模态组合因子FMC=1，文献[10]中βR推荐值为0.05～0.15，对于具有简单振型、单一模态的简单设备，FMC对应的随机性对数标准差取下限值，即βR=0.05。

在设备易损性分析中，2个水平地震分量和1个垂直地震分量用SRSS方法组合，即地震运动的3个分量中每个分量引起的同方向上的最大响应的平方和的平方根。这是一种以中值为中心的方法，则地震分量组合FECC=1，对应的βR为0.18[10]。

综上，FER=0.97，βU=0.14，βR=0.19。

3.4 结构响应因子FSR

谱形状因子FSA表示由于安全停堆地震谱和参考地震谱之间的差异而引起响应的变化。由于直接采用CMT所在位置的时程反应谱作为输入，则FSA=1。厂房对输入地震有放大和滤波作用，楼层反应谱一般变窄变高，其窄高处的频率与厂房主频相对应[7]，则安全壳主频为10 Hz。文献[7]给出了地震响应谱形状对应频率下βU为0.16，βR推荐值为0.18～0.22，本文βR取0.20。

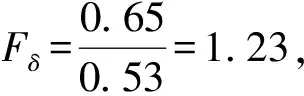
地震条件下构筑物地基上每点在任何时刻的运动均不同。像核电站这类大范围坚硬地基，其地震运动随着高频波穿过土壤/地基而不断衰减，衰减量可用地基尺寸与频率响应构成的函数来表示。通常将特定平面地基尺寸de=45.72 m(150英尺)作为参考值，用衰减因子来保守地表示地面运动不相干性[10]。表2列出de尺寸地基在不同谱频率下衰减因子Rde的推荐值[5]。

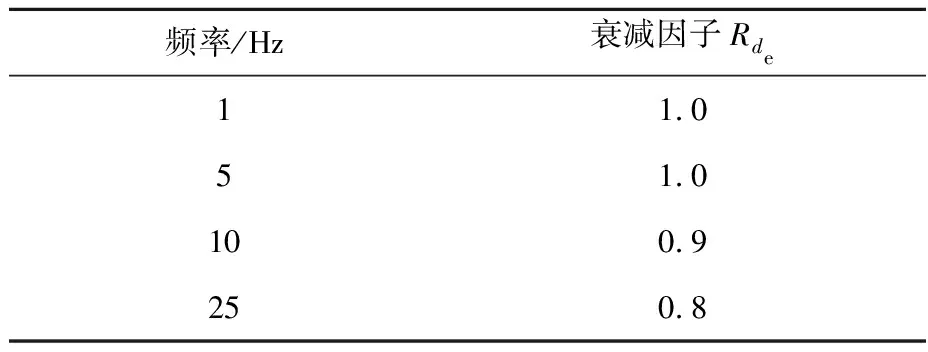
表2 de尺寸地基在不同谱频率下的衰减因子推荐值Table 2 Recommended reduction factor of de-size foundation for different frequencies

对于其他不同的地基平面尺寸d′e，衰减值1-RS可由特定地基平面尺寸de和衰减值1-Rde呈比例地外推获得[5]：

(15)

CMT所在安全壳的屏蔽结构外直径为44.20 m，可得地面运动不相干性FGMI=0.90，对应的βU=0.08。

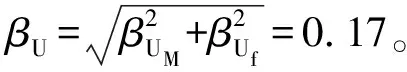
将安全壳模态组合因子FMC考虑为1，βR的取值范围为0.05～0.15[10]，对于具有多个重要模态的结构，采用保守性原则，βR取为0.15。

综上，FSR为1.11，相应的βU= 0.25、βR= 0.32。

3.5 CMT抗震能力计算

根据上述对响应因子的分析计算，可得CMT在韧性失效下的中值安全因子为6.07，对应的不确定性与随机性对数标准差分别为βU=0.31、βR=0.37。AP1000核电站的SSE强度为0.3g，则其抗震能力中值Am= 1.82g，由式(4)可得HCLPF值为0.59g。图4为CMT的易损性曲线。从图4可看出，其具有较强的抗震能力，在SSE强度0.3g下，其失效概率近似为0，由于均值曲线的标准差大于中值曲线标准差，使均值曲线具有更大不确定性，曲线更平坦，从而分布范围更广。

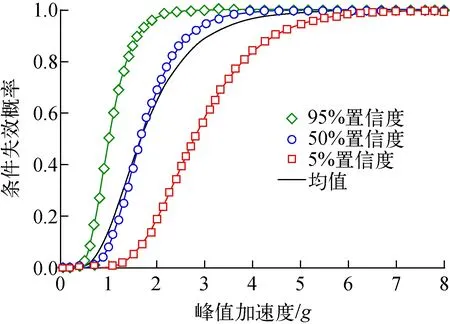
图4 CMT易损性曲线Fig.4 Fragility curve of CMT

3.6 敏感性分析

在易损性分析过程中，需对多个变量进行分析，每个变量均有随机性和不确定性误差。对CMT易损性分析过程中，部分变量是根据推荐范围值结合具体分析而取定的，但这又对结果分析有一定误差。表3列出在上述分析过程中根据范围值而取定的值。

由式(3)、(9)、(11)可知，对于具体的变量因子，均会由SRSS方法组合。因此本文考虑总体不确定性误差与随机性误差对易损性分析的影响。由表3可得随机性对数标准差βR的取值范围为0.33～0.41。

表3 根据范围值而取定的值Table 3 Value based on range value

根据βR的变化范围，绘制了如图5所示的3组CMT易损性曲线，其中虚线βR表示取下限值，实线表示取上述计算值，点线表示取上限值。从图5可看出，βR的变化对条件失效概率值的影响较小，即在分析过程中涉及到易损性参数的随机性误差，可根据范围值取定，简化分析。随着对数标准差值的增加，曲线逐渐平缓，结果不确定性变大。

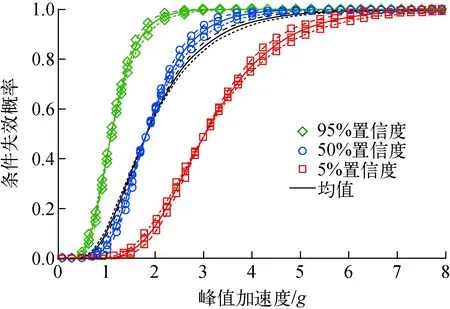
图5 不同βR误差下CMT易损性曲线Fig.5 CMT fragility curve under different βR errors

对于βR取值范围为0.33～0.41，CMT的HCLPF的取值范围为0.56g～0.64g，相对于计算值其相对偏差为-5.08%～8.47%。由式(4)可知，HCLPF值与βR呈反比，减小随机性误差，可提高结果的可靠性，但对结果影响较小。在AP1000概率安全分析报告中，采用确定论方法，基于适当的荷载组合得到的极限设计裕量，考虑CMT支撑结构脆性失效，得到CMT支撑结构的HCLPF值为0.54g[14]，其值略低于采用概率论计算的结果，这与确定论方法中采用大量保守性原则有关。

4 结论

CMT的HCLPF计算值为0.59g，高于核电站SSE强度0.3g，但在分析中若完全考虑保守性，其值为0.56g，也高于SSE下的，说明CMT具有良好的抗震性能。

随机性对数标准差βR对设备的条件失效概率和HCLPF值影响较小，可简化分析过程中对随机性误差的考虑，对结果的可靠性影响较小，使易损性分析更简洁。

在失效模式相同的情况下，CMT采用概率论计算的HCLPF值与采用确定论获取的HCLPF值结果相近，说明了两种方法对于分析设备抗震能力的可靠性。

本文分析了CMT在脆性失效模式下的条件失效概率以及HCLPF值，但对于部分设备可能存在多种贡献程度相近的失效模式使其失效，可针对多种失效模式共同作用做进一步研究。