GPU加速MOC输运计算性能分析研究

宋佩涛，张志俭，梁 亮，张 乾，赵 强

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

特征线方法(MOC)因其几何适应性和天然的并行能力，被广泛应用于反应堆物理数值计算，众多知名堆芯中子学程序均采用了MOC，如CRX[1]、DeCART[2]、nTRACER[3]、MPACT[4]、OpenMOC[5]和NECP-X[6]。但堆芯规模的MOC输运计算耗费大量的计算机资源和计算时间，因此有效的加速手段和高效并行算法是全堆芯MOC计算的重点研究方向。

近年来，图形处理器(GPU)在制造工艺、功耗等方面不断发展，借助英伟达(NVIDIA)推出的统一计算设备构架(CUDA)[7]，GPU功能也逐步从图像处理拓展到了科学计算领域。相比CPU，GPU兼顾通用性、效能和性能等多方面因素，具有更高的浮点运算能力和显存带宽。因此，GPU为加速全堆芯MOC计算提供了新方法和思路。

然而，目前采用GPU加速MOC中子输运计算的研究较少。国外Boyd等[8]、Tramm等[9]、Chio等[10]先后实现了GPU加速二维和三维MOC中子输运计算。国内韩宇[11]和郑勇[12]分别实现了GPU加速六角形几何MOC计算及模块化MOC计算。异构并行方面，张知竹[13]实现了基于多GPU系统的三维MOC计算。以上研究大多侧重于实现GPU对MOC的加速，而进一步的性能分析相对较少。

本文针对二维MOC输运计算，采用CUDA编程规范，实现基于NVIDIA GPU加速MOC计算的并行算法。

1 MOC输运计算

基于平源近似，省略能群标识，特征线形式的稳态多群中子输运方程为：

(1)

其中：φ(s)为中子角通量；Σt为总截面；s为中子穿行方向；Q为源项。

对于式(1)，在平源区内沿s进行积分可得：

(2)

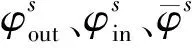
引入积分因子，对式(1)进行解析求解可得步特征线法：

(3)

其中，式(3)中指数项(1-e-Σtls)可通过指数函数和线性插值两种方式进行计算。

采用菱形差分[14]，式(2)中的平均角通量可表示为：

(4)

联立式(2)、(4)可得平均角通量：

(5)

实际计算中，有1组平行射线沿角度Ω穿过平源区n，引入角度离散p，采用数值积分，可求得平源区n的平均中子标通量：

(6)

其中：ωp为求积权重；dp为Ωp方向的射线间距。

2 算法实现

2.1 迭代流程

GPU加速MOC求解流程如图1所示，其基本思路是将计算密集的输运扫描部分移植到GPU并行计算，而计算参数准备和收敛判断等涉及计算流程控制以及逻辑性强的过程则在CPU进行。计算流程为：1) 在CPU进行计算初始化，生成截面、特征线等信息；2) 将计算所需的信息(截面信息、特征线信息等)从CPU一次性拷贝到GPU；3) 在GPU执行平源区源项计算、输运扫描和裂变率及通量残差计算；4) 将裂变率和通量残差从GPU拷贝到CPU；5) 在CPU计算keff，根据前后两次迭代的keff相对变化率和通量残差进行收敛判断。在CPU进行keff计算和收敛判断，相比在GPU进行此过程，多了1个数据拷贝过程(过程4)，该数据拷贝过程时间占比较小(<计算总时间的0.1%)，因此对程序整体效率影响较小。本文之所以在CPU进行keff计算和收敛判断，是为了便于后续研究中多CPU和多GPU异构并行的实现。在多GPU异构并行中，各GPU只负责一部分输运计算任务，全局keff的求解和收敛判断，则需CPU将各GPU求得的裂变率和局部通量残差收集后在CPU进行。

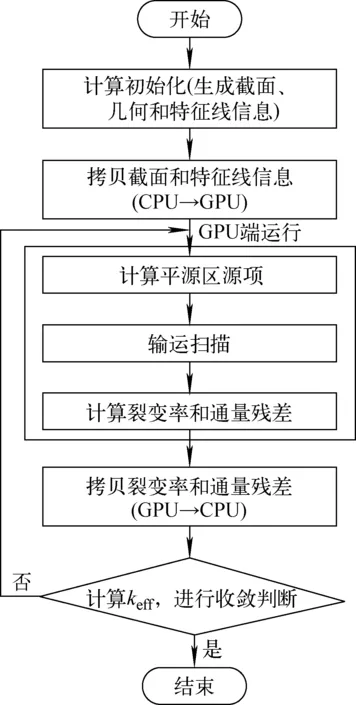
图1 GPU加速MOC求解流程Fig.1 Flow diagram of MOC on GPU

输运扫描部分为整个求解流程的重点，本文采用Jacobi MOC扫描算法进行输运求解，即在输运扫描前更新所有空间区域和所有能群的散射源项和裂变源项，而在单次输运扫描过程中，源项不进行更新。考虑到MOC计算在特征线和能群层次的并行特性，本文所采用的并行策略为特征线加能群并行方式，即单个GPU线程负责单条特征线的单个能群的相关计算。

在CUDA中，将CPU端调用、GPU端执行的函数称为核函数，核函数在GPU线程上执行。GPU线程以线程束形式参与计算，1个线程束中包含若干线程，同一线程束中的线程执行相同的指令。线程束的大小由硬件的计算能力版本决定，对于本文所采用的GPU，线程束大小为32，即32条线程组成1个线程束，执行相同的指令。本文所涉及的输运扫描过程在输运扫描核函数中进行。由于输运扫描计算在整个计算过程中最为耗时(时间占比90%以上)，因此输运扫描核函数的执行性能直接影响程序的整体效率，本文围绕输运扫描核函数的性能进行分析。

2.2 输运扫描核函数

输运扫描核函数负责源迭代过程中的输运扫描计算，其核心思想是将沿某方向贯穿整个求解区域的1条特征线的1个能群的计算任务分配给1个GPU线程，算法过程为：1) 为当前GPU线程分配计算任务，即根据当前线程ID(_tID)确定待求解的特征线ID(_trackID)和能群ID(_groupID)；2) 为当前GPU线程分配共享内存空间；3) 沿当前特征线进行输运扫描。GPU以线程束为单位进行计算，线程束的执行由线程束调度器自动分配，以保证硬件资源的充分利用。因此，开发人员应关注线程束内部的负载均衡。该算法将1条特征线、1个能群的相关计算分配给1个GPU线程。当1个线程束内部所有线程都在执行同一条特征线的不同能群的计算时，该线程束能保证负载均衡；当1个线程束内部涉及不同特征线的计算时，由于不同特征线中线段数量不同，此时就会引入负载不均衡。这种负载不均衡在当前算法下不可避免，但由于单个线程计算量本身较小，这种线程束内部的负载不均衡对整体计算效率的影响得到了一定程度的缓解。

输运扫描过程中，当前特征线段出/入射点间角通量的变化量采用步特征线法和菱形差分两种方法求解，而针对步特征线法中指数项的求解，分别采用指数函数计算和线性插值计算。

GPU同时提供了强大的单精度和双精度浮点运算能力。因此在输运扫描核函数的实现过程中，考虑了不同浮点运算精度对程序计算精度和效率的影响。结合GPU硬件特性，在输运扫描核函数实现过程中采用了如下几项处理方式。

1) 使用GPU共享内存存储角通量信息

输运扫描过程中，特征线段出射角通量随计算过程不断更新，对应角通量数组频繁的读/写操作。从硬件角度来讲，相比GPU显存，作为片上存储器的共享内存具有更高的访存带宽和更小的访存延迟。因此，将角通量数组存储在共享内存。

2) 采用不同精度进行原子操作

平源区特定能群的标通量按照数值积分过程由不同方向上特征线段的角通量加权求和获得，该过程涉及不同线程向同一全局内存地址写入数据。为保证数据写入的准确性，CUDA提供了读取-修改-写入的原子操作。原子操作定义为：不会被线程调度机制打断的操作。1个原子操作过程包括3部分：从某个地址读取数据；将该数据加某一特定值；将修改后的数据写回原地址。原子操作保证了上述3步操作过程不会被其他线程打断，即相关线程顺序访问同一内存地址。CUDA在双精度和单精度下均提供了原子操作功能，且不同浮点运算精度下访存带宽不同。因此可在整体采用双精度的情况下，采用单精度声明标通量数组scalarFlux[]，并在原子操作部分采用单精度，即采用混合精度进行计算。

3) 采用不同精度进行指数函数计算

对于步特征线-指数函数核函数，其计算过程中涉及指数函数计算。CUDA在双精度和单精度情况下提供了不同的指数函数。相对双精度，单精度指数函数计算更快，但精度略有损失。因此，在步特征线-指数函数核函数中，整体采用双精度计算时，指数函数可采用单精度计算，即采用混合精度方式计算。

本文针对菱形差分、步特征线-指数函数和步特征线-线性插值3种核函数，对应双精度、混合精度及单精度分别测试不同组合方式对程序计算精度和计算效率的影响。表1列出不同核函数和不同精度的组合说明。需要注意的是，为保证特征线信息的准确性，在特征线信息生成过程中采用双精度进行生成，而对于整体采用单精度的计算过程，特征线信息存储时采用单精度进行截断。

3 性能分析

NVIDIA提供了CUDA程序性能分析工具集，便于用户对GPU程序进行调试及性能分析。为量化当前程序对GPU硬件的使用程度并识别当前程序的性能瓶颈，本文借助nvprof性能分析工具，对3种输运扫描核函数在不同精度下的性能进行分析，性能分析指标列于表2。

分析线程束指令签发阻断原因可辅助识别程序的性能瓶颈。对于每个时钟周期，线程束调度器都会尝试向线程束签发1条指令，当线程束由于某种原因处于不可用状态时，指令签发则会被阻断。造成指令签发阻断的因素主要包括访存相关和执行相关。访存相关指待签发指令正在等待访存完成，造成签发阻断；执行相关指待签发指令正在等待前序指令执行完成，以提供待签发指令执行所需的参数，造成签发阻断。

4 数值计算

本文采用二维C5G7基准题[15]进行测试与分析，图2示出该基准题的1/4堆芯和燃料组件布置。整个计算区域在x和y方向分别被划分为51个栅元，每个栅元采用如图3所示的网格划分。每个象限选择14个方位角和3个极角，使用Tabuchi-Yamamoto极角求积组。

表2 性能分析指标Table 2 Metrics for performance analysis

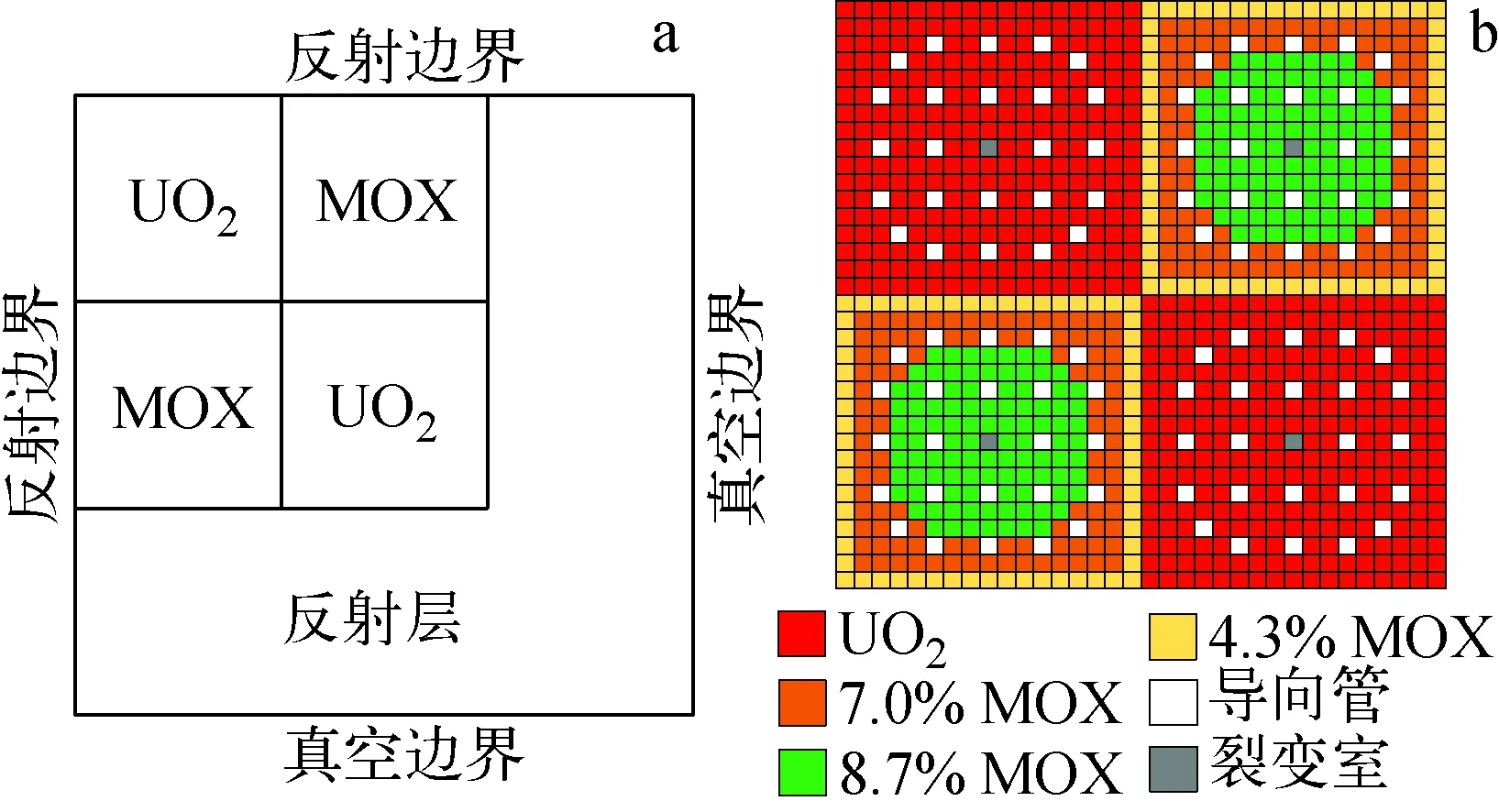
图2 二维C5G7基准题1/4堆芯布置(a)和燃料组件布置(b)Fig.2 Core configuration (a) and fuel pin composition (b) for 2D C5G7 benchmark problem

keff和通量收敛准则分别设置为10-6和10-5。计算平台采用多核工作站，硬件及相关参数列于表3。

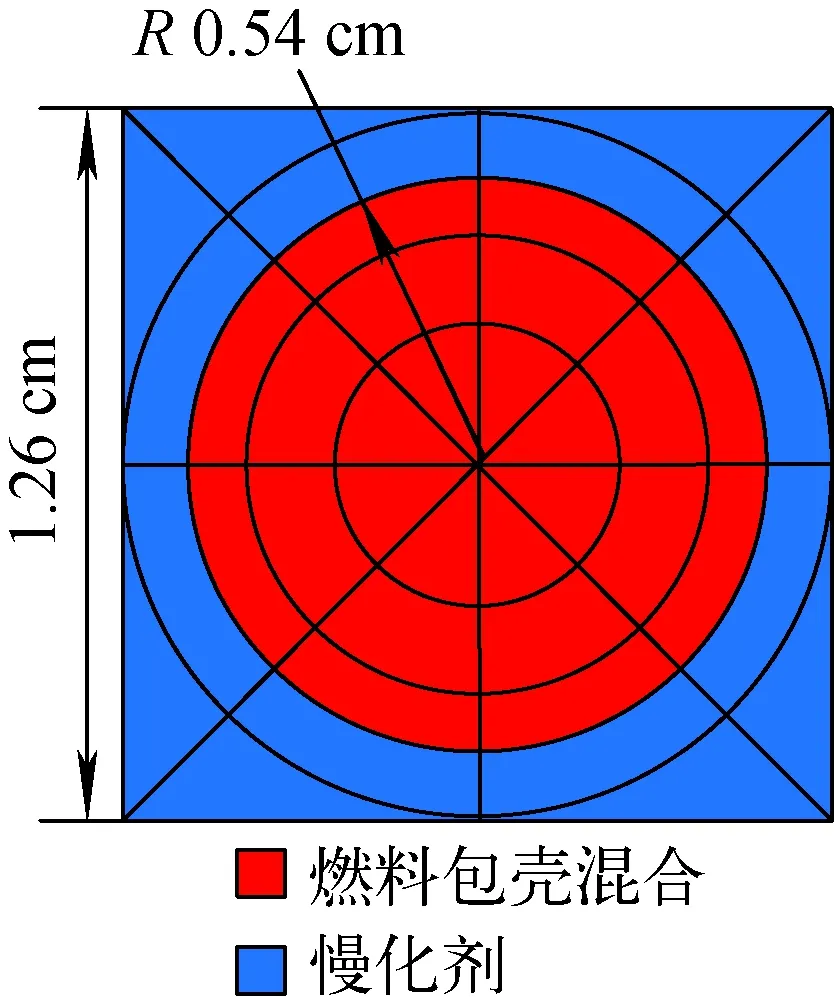
图3 栅元组成及网格划分Fig.3 Fuel pin layout and mesh

表3 计算平台参数Table 3 Parameter of computing platform

4.1 计算精度和效率测试

不同测试情况下，keff、栅元功率及组件功率误差列于表4，参考解来源于MCNP。表4中，MAX Error为最大棒功率相对误差，AVG Error为平均棒功率相对误差，RMS Error为棒功率均方根误差，MRE Error为平均相对误差。对于菱形差分和步特征线法，由于方法不同，keff计算结果相差约8 pcm。由表4可见：本征值和功率分布误差均在合理范围内；采用混合精度和单精度浮点运算，相对于同等计算条件下的双精度浮点运算结果，由于精度损失引入的误差较小，均低于收敛准则。可见，对于二维C5G7基准题，在输运求解部分，不同的浮点运算精度均能满足计算精度要求。

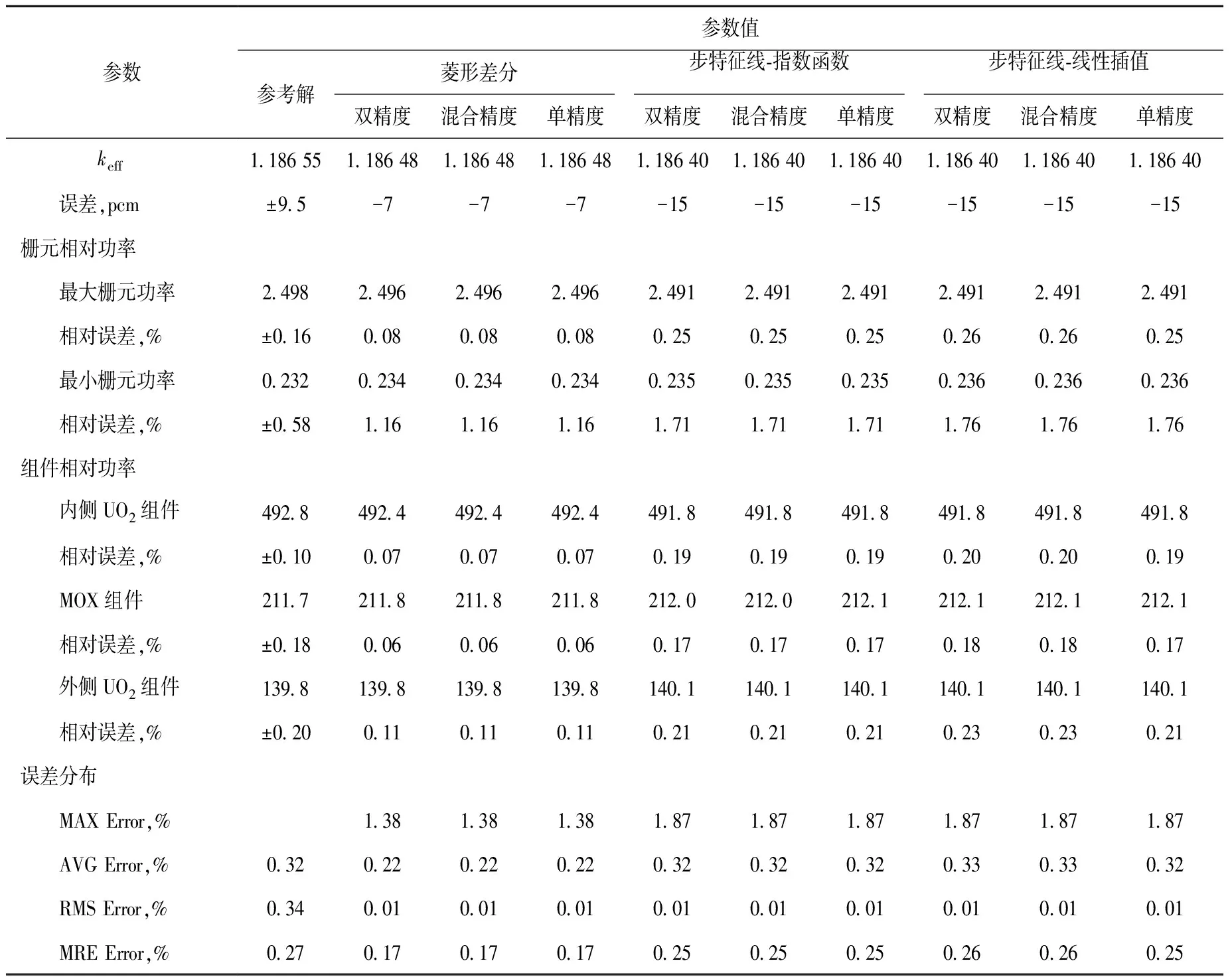
表4 二维C5G7基准题特征值及功率分布的结果Table 4 Result of eigenvalue and power distributions for 2D C5G7 benchmark problem

4.2 输运扫描核函数性能分析

本文分析了3种类型输运扫描核函数在3种浮点运算精度下的性能特点，识别了GPU硬件使用程度及程序的性能瓶颈。

1) 计算效率分析

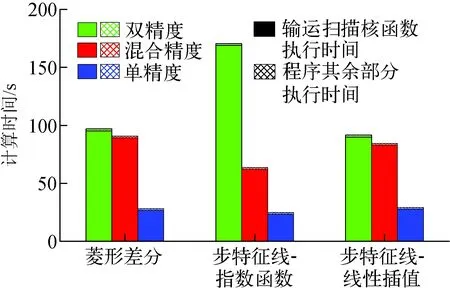
图4 二维C5G7基准题计算时间Fig.4 Runtime of 2D C5G7 benchmark problem

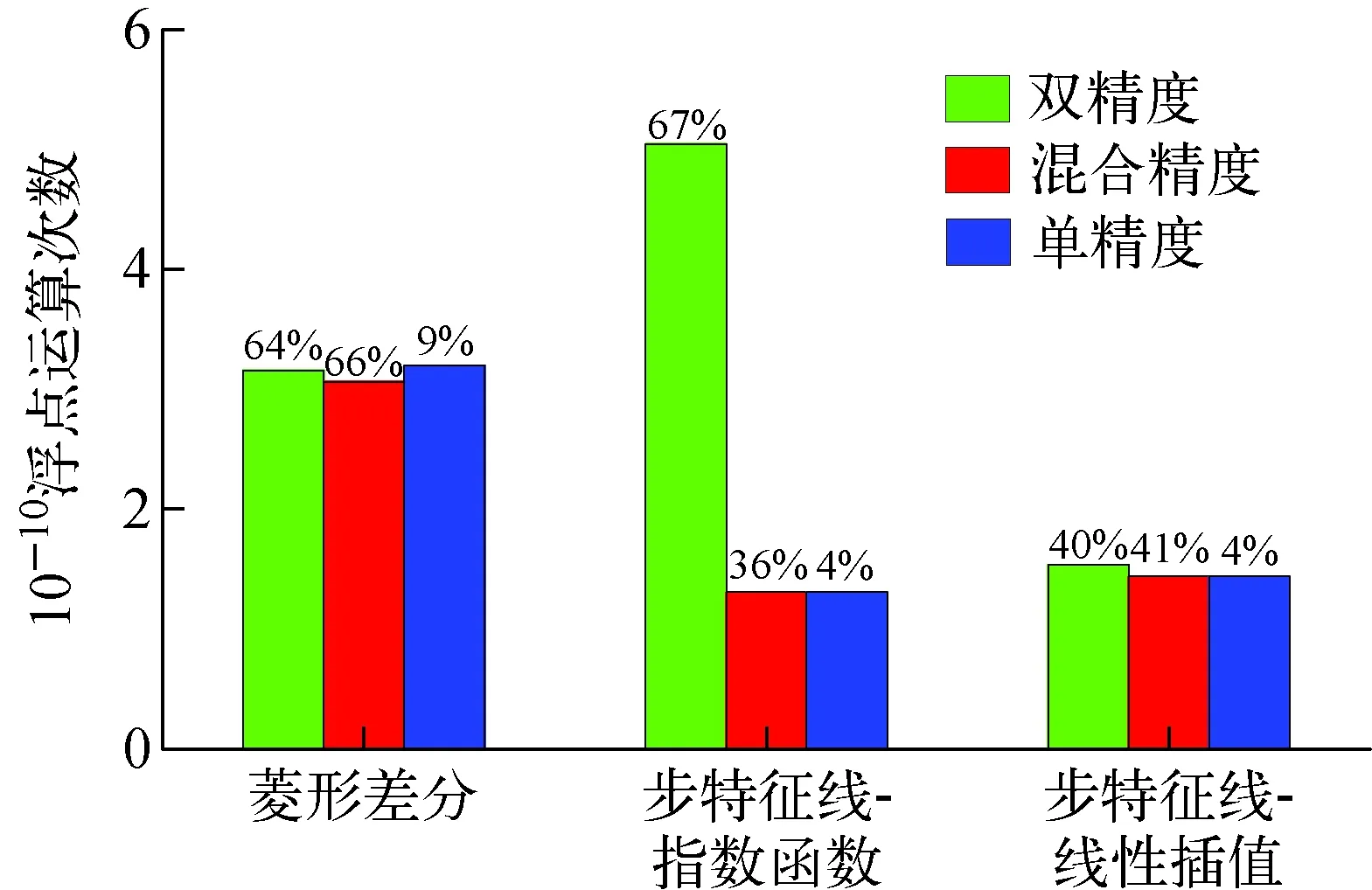
图5 二维C5G7基准题浮点运算次数及浮点运算效率Fig.5 Count and efficiency of floating octal point for 2D C5G7 benchmark problem

图4示出程序整体计算时间，包括输运扫描核函数执行时间和程序其余部分执行时间，其中输运扫描核函数占到总计算时间的90%以上。图5示出程序浮点运算次数和浮点运算效率，其中柱状图表示浮点运算次数，其顶部数据表示浮点运算效率。图6示出L1和L2缓存命中率。

图6 二维C5G7基准题L1和L2缓存命中率Fig.6 L1 and L2 cache hit rates for 2D C5G7 benchmark problem

在双精度情况下，由图4可知，菱形差分和步特征线-线性插值计算效率相当，而步特征线-指数函数计算最为耗时。这是由于在双精度情况下，步特征线-指数函数中指数函数的计算具有较大的浮点运算量，因此，在如图5所示浮点运算量中，步特征线-指数函数在双精度情况下的浮点运算量要明显多于其他核函数。在双精度情况下，步特征线-线性插值性能最优。

在混合精度情况下，输运扫描核函数中标通量数据的读/写操作(其中写为原子操作)均在单精度下完成，图5所示的浮点运算次数相对于双精度情况有所下降；同时，由于单精度访存操作具有更高的访存效率，因此相较于双精度情况，L1和L2缓存命中率均有所提升(图6)。运算量的减少和缓存命中率的提升共同导致了计算效率的提升，因此在图4中可看到混合精度情况下的计算时间相比双精度计算有所下降。此外，造成步特征线-指数函数性能明显提升的另一关键因素是单精度形式指数函数的使用，这使得浮点运算次数大幅下降(图6)，从而导致了计算效率的提升。结果表明：在混合精度情况下，相对于双精度计算，引入单精度标通量数据读/写操作的加速效果约为1.07倍；而在步特征线-指数函数中引入单精度指数函数计算的加速效果较为明显，约为2.6倍。在混合精度情况下，步特征线-指数函数性能最优。

在单精度情况下，3种核函数的计算效率相对于双精度和混合精度情况有显著提升，步特征线-指数函数效率优于另外两种核函数。

2) 性能瓶颈分析

输运扫描核函数在不同精度下表现出不同的性能瓶颈。图7示出硬件浮点运算单元利用率及访存效率，图8示出造成线程束指令签发阻断的原因。

图7 二维C5G7基准题浮点运算单元利用率及访存效率Fig.7 Arithmetic function unit utilization and DRAM efficiency for 2D C5G7 benchmark problem

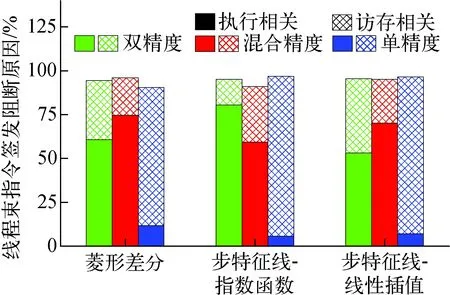
图8 二维C5G7基准题线程束指令签发阻断原因Fig.8 Warp issue stall reason of 2D C5G7 benchmark problem

在双精度和混合精度情况下，如图7所示，硬件双精度浮点运算单元利用率均达到100%。结合图8可知，60%以上的线程束指令签发阻断由执行相关因素引起，即待签发指令多数情况下在等待前序指令执行完成。同时分析图5所示的浮点运算效率可知，在双精度和混合精度情况下，3种类型核函数均达到了较高的双精度浮点运算效率(其中步特征线-指数函数在混合精度情况下效率较低，约36%)。因此，核函数在双精度和混合精度情况下表现为指令密集型，密集的指令操作是其性能瓶颈。

在单精度情况下，由于本文使用的GPU具有强大的单精度浮点运算能力(单/双精度峰值浮点运算能力之比为32∶1)，更大的单精度指令吞吐量导致了更高的计算效率。但程序的单精度浮点运算效率不足硬件峰值的10%(图5)，同时图7所示的硬件单精度浮点运算单元利用率不足40%，因此，密集的指令不再是制约程序性能的瓶颈。分析图8可知，单精度情况下造成线程束指令签发阻断的主要因素为访存相关(约90%)，而图7所示的访存效率尚未达到15%，可见制约程序性能的并不是访存带宽，而是访存延迟。

若以浮点运算效率(实际达到的硬件峰值计算能力的百分比)衡量GPU硬件利用率，则如图5所示，输运扫描核函数在双精度和混合精度情况下具有较高的硬件利用率(36%～67%)，在单精度情况下硬件利用率较低(4%～9%)。

3) GPU对CPU加速效果分析

为对比GPU相对CPU计算的加速效果，表5列出采用不同类型核函数及不同浮点运算精度情况下，单CPU线程和单GPU的总计算时间对比，同时给出了相同计算条件下单GPU对单CPU线程的加速效果。从加速效果看，双精度和单精度情况下，单GPU对单CPU线程加速效果分别达到35倍和100倍以上。

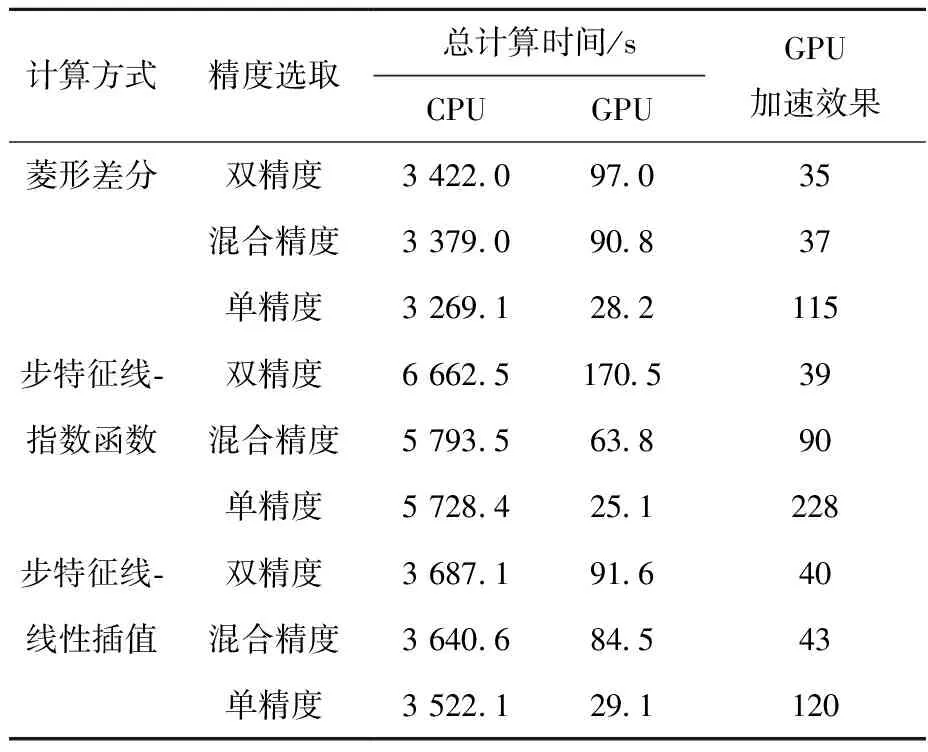
表5 不同类型核函数及浮点运算精度下的计算时间Table 5 Runtime under different kernel functions and floating-point precisions

本文实现了单CPU绑定单GPU，将计算密集的输运扫描部分移植到GPU进行并行计算，计算流程控制等逻辑相关工作仍在CPU进行。在计算过程中，由CPU进程绑定GPU，控制GPU进行相关计算，GPU以独立的加速单元形式存在，输运扫描过程完全在GPU独立执行。当涉及多个GPU并行时，这种由CPU进程绑定GPU，控制GPU进行相关计算的基本模式不会改变。且在多GPU并行时，各GPU的计算理应相互独立，所涉及的耦合部分则通过与GPU绑定的CPU进程来完成。各GPU所执行的计算任务仍为局部问题的输运扫描计算，因此，本文涉及的针对GPU的算法和相关性能分析在多GPU并行计算中仍适用。

5 结论与展望

本文实现了基于GPU的二维MOC并行算法，结果表明：程序具有良好的计算精度，不同的浮点运算精度均能保证二维C5G7基准题在输运求解方面的精度要求；采用双精度运算时，步特征线-线性插值计算性能最优；采用混合精度和单精度运算时，步特征线-指数函数计算性能最优。双精度及混合精度情况下，输运扫描核函数性能瓶颈在于密集的指令运算；而在单精度情况下，输运扫描核函数性能主要受访存延迟的影响。从加速效果来看，双精度和单精度浮点运算情况下，单GPU对单CPU线程加速效果分别达到了35倍和100倍以上。本文涉及的算法及相关结论可推广到多GPU并行计算，未来可侧重基于大规模CPUs-GPUs异构系统的并行算法研究。