舵机故障影响分析及容错控制研究*

杨云刚，赵军民,2,刘钧圣,2,王 琨,王齐双

(1 西安现代控制技术研究所, 西安 710065; 2 西北工业大学, 西安 710072)

0 引言

舵机是控制系统的执行机构,是导弹实现精确制导、快速机动的关键[1]。一旦舵机出现故障,导弹必然偏离正常的飞行轨迹,无法完成既定的攻击任务。因此,对舵机进行容错控制[2]具有十分重要的工程意义,是提高导弹姿态控制系统工作可靠性的重要手段[3]。容错控制分为硬件冗余容错控制和解析冗余容错控制,硬件冗余容错控制需要增加系统硬件成本、体积和重量,对导弹作战性能造成负面影响[4];通过重构控制律解析冗余容错控制,从而使导弹按原先正常轨迹飞行。

文中以某型空地导弹为研究背景,研究分析了“X”型布局的舵机故障对导弹控制性能的影响,并分别针对1片舵机故障和2片舵机故障情况提出容错控制算法。该算法能在舵机故障时对正常舵机指令重新分配,补偿故障舵机带来的干扰,从而维持导弹正常有控飞行,直至命中目标。

1 舵机故障影响分析

1.1 舵指令分配模型

以“X-X”型布局的倾斜稳定导弹为研究对象,控制系统生成俯仰、偏航、滚转三通道控制指令,并按一定的分配关系转换为4片舵机的舵指令,舵面偏转实现导弹三轴姿态控制。如图1所示,从弹尾向前看,4片舵机后缘向上偏转为正,产生正的控制指令。

图1 舵偏角正向偏转示意图

根据极性定义,俯仰、偏航、滚转三通道控制指令与4片舵指令的转换关系为:

(1)

其中,δx、δy、δz分别为滚转、偏航和俯仰控制指令,δ1、δ2、δ3、δ4分别为4片舵机控制指令。

根据上述方程特点,获得三通道控制指令后,4片舵指令可有无穷多种组合。因此,采用Moore-Penrose 伪逆法[5-7],求得其最小范数解,即:

(2)

1.2 舵机故障检测

工程应用中常将舵机简化为一个二阶模型[8],当通过数学模型计算得到的舵偏与实际舵反馈误差大于一定阈值时,认为舵机出现故障,则有:

(3)

其中,K为比例系数;τ为时间常数;δi为第i片舵机对应的舵指令;fδi为第i片舵机对应的舵反馈;k为经验系数,一般取0.1～0.2。

1.3 舵机故障影响分析

不失一般性,以1舵卡死为例,若不采取容错控制算法,则控制系统实际得到的三通道等效舵偏为:

(4)

式中:δ′x、δ′y、δ′z为控制系统实际三通道等效舵偏,δx、δy、δz为控制系统需要的三通道等效舵偏。由式(4)可知,当一片舵机故障时,该舵偏在俯仰、偏航、滚转三通道均叠加了干扰力矩,力矩大小与故障时舵偏及应分配的舵指令相关。若不采取容错控制措施,则导弹不能按预定控制规律正常飞行,最终脱靶,甚至失控落地，造成安全事故。

同理,以1舵、2舵两片舵机卡死为例,若不采取容错控制算法,则控制系统实际得到的三通道等效舵偏为:

(5)

由此可见,当出现舵机故障时,若不采取容错控制措施,按原有控制律进行制导飞行,则故障舵偏会在三通道均产生干扰力矩,影响导弹姿态控制和正常飞行。

2 容错控制研究

文中容错控制策略基本思想为:实时采集舵反馈,与理论计算的舵偏比较,在线进行舵机故障检测。若舵机工作正常,则按式(2)分配律进行舵指令分解,若舵机出现故障,则按下文容错控制算法进行舵指令分配,补偿故障舵偏引起的干扰力矩,从而维持导弹正常飞行。

将现有16级机械设计专业2016学年的成绩总表，与系部上交的2017学年第一学期成绩合并到一起。具体步骤如下：16机械设计成绩总表中新增2017学年第一学期的科目名称顺序与班级上交的成绩表科目顺序一致，在N2单元格中输入“=VLOOKUP(B2,'[16机械设计与制造班.xlsx]16机械设计'!B6:J39,3,0)”即可得到机械设计基础科目的成绩，依次类推，分别可得到互换性与技术测量、现代企业管理、心理健康教育、电工电子技术和应用文写作的成绩。

2.1 单片舵机故障时容错算法设计与分析

不失一般性,以1舵卡死为例,当故障出现时,以故障舵偏为约束,则有

(6)

由于det(A1)≠0 ,对式(6)求逆可得:

(7)

结合式(2),由式(7)得到容错控制算法如式(8):

(8)

其他舵机中任意一片出现故障时,同理可得类似结果。观察式(8)可知,当1片舵机出现故障时,新的分配律保持故障舵机指令不变,同时将故障舵机产生的干扰分解到其他3个正常舵机上。将式(8)代入式(1),易知:

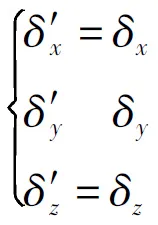
(9)

对比式(9)与式(4),按上述容错控制算法分配的舵指令执行,故障舵机给三通道等效舵偏产生的干扰力矩消失,导弹综合控制效果保持不变,可继续正常飞行命中目标。

2.2 两片舵机故障时容错算法设计与分析

不失一般性,以1舵、2舵两片舵机卡死为例,进行容错控制算法设计。由于未知数数量少于约束条件数量,此时方程已无解,即仅靠两片舵机工作无法完成三通道控制,因此只能对约束条件进行取舍。

暂不考虑滚转通道控制,以故障舵偏为约束,则有:

(10)

通过求逆可得:

(11)

同理暂不考虑偏航通道控制,以故障舵偏为约束,可得:

(12)

综合考虑导弹控制性能,结合式(11)和式(12),可得1舵、2舵卡死时的容错控制算法为:

(13)

式中,k1,k2为经验系数,满足k1+k2=1。当其他舵机中任意2片出现故障时,同理可得类似结果。新的分配律保持故障舵机指令不变,同时将故障舵机产生的干扰分解到其他3个正常舵机上。将式(13)代入式(1),易知:

(14)

对比式(14)与式(5),按上述容错控制算法分配的舵指令执行,补偿了故障舵机在俯仰通道产生的干扰力矩,而滚转和偏航通道存在一定干扰。由于俯仰通道控制效果保持不变,因此,即使上述算法无法保障导弹按原轨迹飞行,但若故障出现在弹道末端,依然可控制导弹俯冲接近甚至命中目标。

3 仿真验证

以某型空地导弹攻击地面横向运动目标为例,导弹发射后先爬升,达到预定弹道高度后平飞,接近目标时转入比例导引,俯冲攻击命中目标。

首先假设导弹发射后40 s时1舵出现故障,卡死在1.6°位置。如图2所示,导弹转入比例导引,弹道开始下压后,如果不采取容错控制措施,导弹按照原控制律进行飞行,则姿态角出现较大扰动,最终脱靶量达到8.3 m,无法完成毁伤目标的目的。采取文中容错控制算法后,其余舵机完全补偿了1舵故障产生的干扰力矩,导弹姿态角与原正常飞行时一致,导弹脱靶量为0.07 m,命中目标。仿真计算结果与理论分析相符。

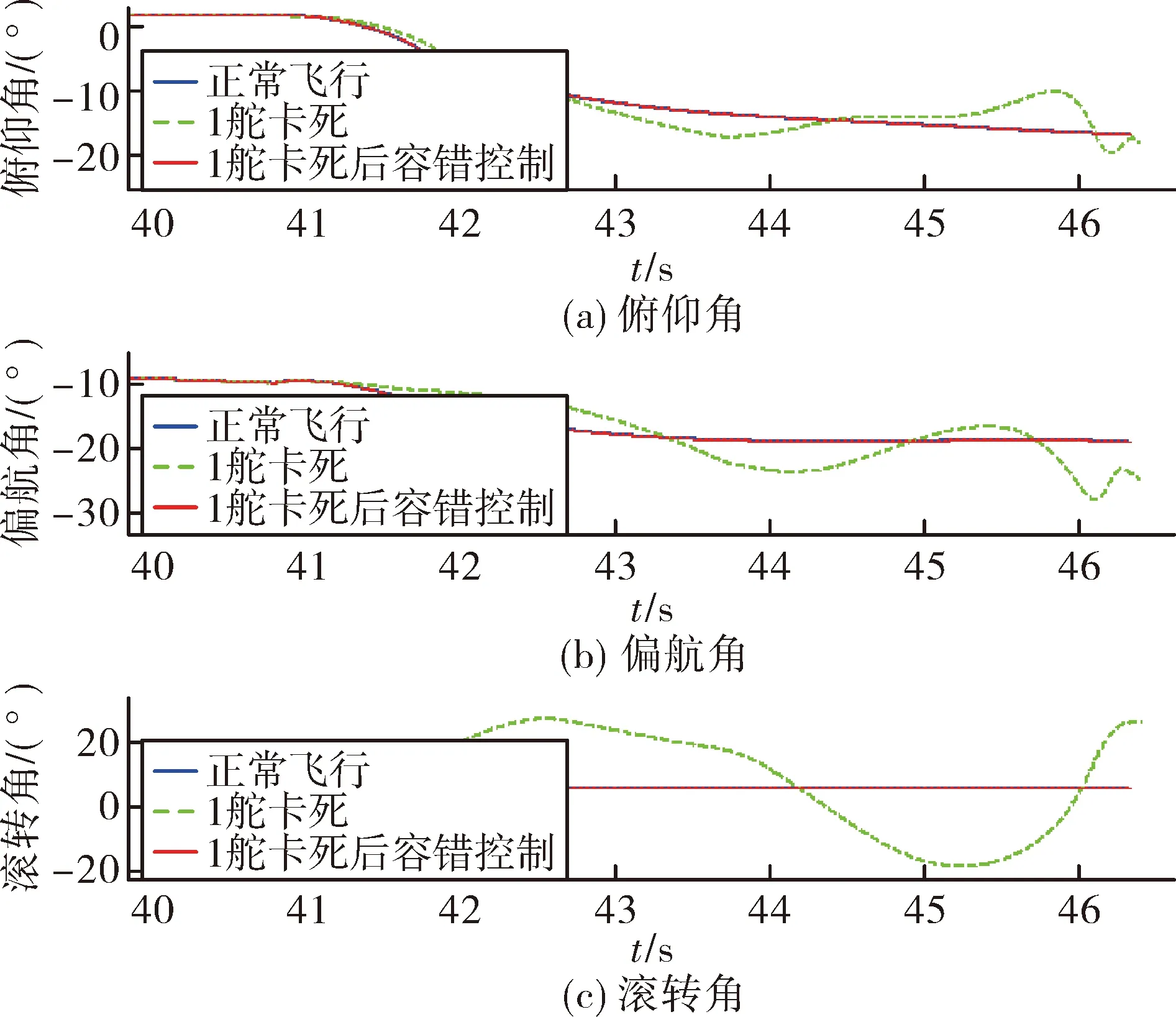
图2 1片舵机故障情况导弹姿态角对比

其次假设导弹末制导段飞行到44 s时1舵、2舵同时出现故障,分别卡死在-0.2°和1.1°位置。如图3所示,如果不采取容错控制措施,导弹按照原控制律进行飞行,则俯仰、偏航、滚转三通道均受到干扰力矩影响,导弹失控远远偏离正常姿态,最终脱靶量达到2.3 m。采取文中容错控制算法后,虽然无法完全消除故障舵机产生的干扰,但影响量值明显降低,导弹姿态接近正常轨迹,最终脱靶量0.7 m,命中目标。仿真计算结果与理论分析相符。

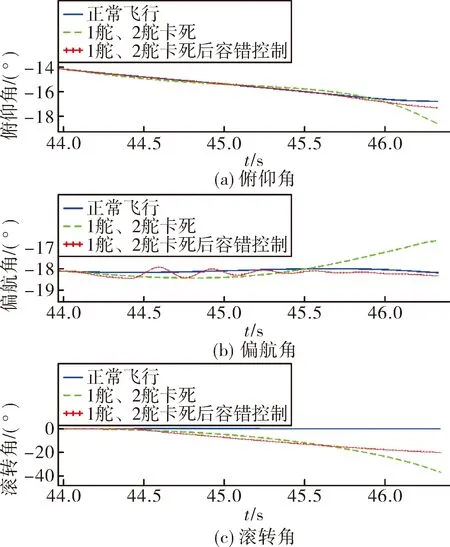
图3 2片舵机故障情况导弹姿态角对比

4 结论

以某型空地导弹为背景,采用Moore-Penrose 伪逆法建立了“X”型布局舵机舵指令分配模型,研究分析了舵机故障对导弹飞行的影响机理,提出针对1片舵机故障的容错控制算法和针对2片舵机故障的容错控制算法,仿真计算结果验证了算法的有效性。文中的研究对于提高导弹系统工作可靠性具有工程应用价值。