面向宏观基本图的多模式交通路网分区算法

傅 惠，王叶飞，陈赛飞

(1.广东工业大学 机电工程学院，广东 广州 510006；2.澳门科技大学 系统工程研究所，澳门特别行政区 999078)

多模式宏观基本图是以宏观基本图(macroscopic fundamental diagram，MFD)[1]为基础，通过宏观交通流参数反映路网内社会车和公交车总体运行性能的基本工具。主要体现社会车流、公交车流在不同密度(或累计车辆数)组合情况下，对网络整体车流量或客流量的影响关系。多模式宏观基本图研究的意义在于，从子区视角而非路口视角进行交通流规律分析，降低了对全路网交通要素检测数据完备性的要求，更利于实现对大规模路网交通特性的整体性认识。比如，可通过估测到的区域平均速度、密度或流量等参数，来刻画该区域的宏观交通流规律。与此同时，通过多模式宏观基本图揭示的不同交通模式组成比例对路网总体性能的影响，有可能为现实多模式交通流的集成控制提供一条可行路径。目前学术界对公交车与社会车之间的作用关系，无论从微观还是宏观层面的研究都不够深入。这使得在社会车流交通控制研究中对公交车的干扰影响考虑不足，而忽略社会车流影响的城市公交调度效果也受到明显制约。有关多模式宏观基本图形的理论研究，目前主要集中在其存在性、影响因素、拟合方法等方面。比如，文献[2-3]研究实际路网中不同模式交通流的运行特征和总体表现；文献[4-5]侧重不同路段多模式交通流的分布对整体性能的影响。相关应用研究，如文献[6-7]通过边界收费和停车收费的控制手段，使得区域路网运行效率更高。

MFD研究的经验表明，通过有效分区获得匀质子区从而估计得到子区相应低散射MFD图形(包括抛物线形、三角形、梯形等形状)，是MFD从理论研究转向实际应用的基本前提。文献[8]提出当区域路网中路段的速度(或密度)方差较大时，宏观基本图形会出现高散射和磁滞环(hysteresis loop)现象，这意味着为得到理想低散射的宏观基本图，需将路网中的路段按其速度(或密度)聚集成多个方差较小的区域。多模式路网分区研究尚未见诸文献，归纳其分区原则应具备以下特征：1) 子区内各路段之间应保持联通；2) 子区内多模式交通流均匀性较强，如最小化子区内路段不同模式速度(或密度)的方差。3) 子区规模及其形状尽可能地有利于交通控制与管理。基于类似原则，文献[9]根据单模式MFD理论提出“初始分区-子区合并-边界调整”的三步法，在初始化步骤利用谱方法对子区进行初步划分，再利用考虑邻接区域相似度的合并算法合并子区，最后根据区域形状对边界路段进行调整。需要说明的是，该算法在初始分区和子区合并步骤中，仅考虑邻接路段和邻接子区的方差关系，易导致将不同拥堵程度的路段划分在同一子区。另外，该算法只考虑社会车流的速度(或密度)，不适用于多模式交通路网分区。

为此，本文提出面向多模式MFD的交通网络分区算法，构造用于多模式交通流异质性度量的计算公式，以深圳交通网络为例，对初始化子区算法、子区合并算法、整体分区算法与以往算法进行对比测试。在此基础上，利用多检测器数据融合对子区路网中的多模式MFD进行了实证研究。

1 算法介绍

1.1 算法框架

本文提出的多模式交通路网分区方法，具体包含初始子区划分算法、多子区合并算法和子区边界调整算法，整体算法流程如图1所示。算法参数输入包括：初始分区数NR、最终分区数MR、路段集合XL、路段公交车速度集合VB、路段社会车速度集合VC。

1) 利用区域生长算法(region seeds growing, 简称RSG算法)[10]与综合评价法(technique for order preference by similarity to an ideal solution, 简称TOPSIS)[11]进行子区初始划分，子区中心的位置和数量分别根据XL和MR确定。在区域生长过程中，以社会车速度方差、公交车速度方差和路段到子区中心的距离作为评价指标，依次选取每步的最优路段放入区域中，直到区域所有的路段都有所属的区域，详见2.2节。

2) 利用遗传算法与TOPSIS算法相结合将初始化子区逐步合并为NR个区域。算法中的交叉、变异操作根据初始化子区的邻接关系进行设计；在评价染色体适应度时，以各染色体与正理想解的距离作为虚拟适应度，其中的正理想解在每一步的迭代过程中不断更新，详见2.3节。

3) 识别在区域边界且与本区域只有较少路段相连的路段k，尝试调整该路段的所属区域，如果调整结果比原先结果优则保留调整结果。边界调整算法将重复迭代调整边界路段所属分区，直至分区性能指标不再改善为止。

1.2 基于RSG+TOPSIS算法的初始子区划分

路网分区，本质上是根据路段的特定交通流属性对路段进行合理聚类。对于大规模路网涉及到的路段数量庞大，路段组合可能性空间巨大造成算法复杂度较高。为合理控制合并算法的可行解空间，降低分区算法总体计算量，本文采用RSG+TOPSIS算法进行初始子区划分。该算法既考虑路段邻接关系，也考虑路段与初始子区的整体关系，更为重要的是综合评价法能兼顾两种交通模式的分区性能指标。

RSG算法作为图像分割技术的一种，最早用于集合相似性像素以构成区域。其算法过程如下。1)在每个需要分割的区域中利用K-means算法得到的聚类中心作为生长的中心；2) 将种子像素邻域中与种子有相似性质的像素合并到种子像素所在区域，并作为新像素；3) 以新像素继续向四周生长，直到所有满足条件的像素都被包含起来。由于这种思想与多模式网络分区思想(将具有相似特性的路段集合起来构成路网子区)一致，因此，本文采用RSG算法进行初始子区划分。

图1 多模式交通路网分区算法流程Figure 1 Partitioning algorithm for multi-mode road network

在初始子区划分过程中，需要同时考虑社会车速度方差、公交车速度方差以及子区形状。由于3个指标的数值范围与单位均不相同，因此，简单的加权相加难以凑效。为此，利用TOPSIS算法检测优化目标与最优解、最劣解的距离来评价方案的总体效果。子区初始划分过程分为3个步骤。

1) 根据路段的地理位置利用K-means算法，确定初始化子区的聚类中心。其公式如下

其中，cennr为第nr个子区的聚类中心路段，XL为所有路段集合，NR是初始化子区的数目，SRnr是第nr个子区的路段集合。

2) 选取任一子区nr，识别该子区的邻接路段，作为备选路段集合。其公式如下

其中，SAnr为nr子区的备选路段集合，Adl为识别边界路段的函数。

3) 计算备选路段集合SAnr中各路段的多模式速度方差乘积和到聚类中心的距离，利用TOPSIS算法选取最优路段放入SRnr集合中，其规范决策矩阵构造如下

其中，Mnr矩阵为备选路段集合的规范决策矩阵，和是子区SRnr的社会车速度集合和公交车速度集合，和是备选路段k的社会车速度和公交车速度，dis为计算路段k到聚类中心cennr的距离。

在此基础上，构造加权规范矩阵并计算各路段到正理想解与负理想解的距离。

其中，smkj是加权规范矩阵，wj是j属性的权重，min(Mjnr)和max(Mjnr)分别是j属性的正理想解和负理想解，和分别是第k个路段到正理想解和负理想解的距离。

根据各路段的综合评价指数，选取综合指数最优的路段k*，并将其放入路段集合SRnr，计算公式如下

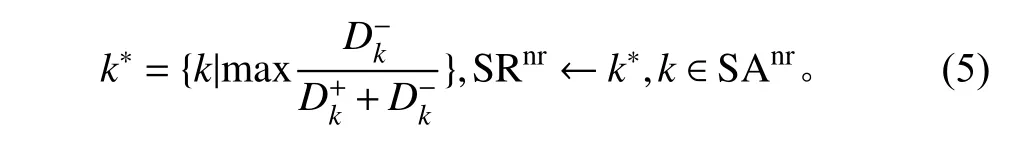
根据以上迭代策略，每次选取一个路段加入到子区SRnr中，直至所有路段皆有所属子区。

1.3 基于GA+TOPSIS算法的子区合并

根据初始化子区结果，以最小化2种模式速度方差为目标，在保证同一区域内的子区地理上相邻的前提下，优化子区之间的组合方式，具体目标函数为：其中，和分别是区域mr路段的社会车速度和公交车速度集合，和分别是区域mr中社会车路段数和公交车路段数。

对于多目标优化问题，通常将其转化为单目标，或求解Pareto最优解集。对于转化为单目标的方法，通常是将多个目标根据重要程度进行加权[12]。若涉及到各目标值取值范围及量纲不同的问题，各目标值权重的确定往往十分困难。对于求解Pareto最优解集的方法，通常使用NSGA或NSGA II算法[13]，根据排序规则从中挑选出折中解或较优解。其不足之处如下。

1) 计算复杂度高。NSGA和NSGA II算法的计算复杂度分别为O(mN3)和O(mN2)，2种算法复杂度高的原因在于每一步的迭代优化都需要进行非支配排序。

2) 搜索效率低下。所得Pareto最优解集中，各个最优解之间无法进行优劣比较，其特点为在无法改进任何目标函数的同时不削弱至少一个其他目标函数，这样的搜索策略是无方向性的。若公平考虑各目标，则解集中带有偏向性的解均为无用解。

3) 可能陷入局部最优。由于Pareto解集是离散的，因此，可能会错过给定排序规则的最优解。特别地，对于本文这种可行解较多组合问题，非支配解的搜索是相当困难的。

针对以上不足，本文在多目标优化中利用了综合评价与遗传算法相结合的方法，得到该排序规则下的最优子区组合方式。基本思想如下。1) 随机产生规模为N的初始种群，计算种群中个体的多模式指标并更新最优解和正负理想解；2) 以各染色体到正理想解的距离作为虚拟适应度，并以此复制染色体；3) 基于子区的邻接关系进行遗传算法的选择、交叉、变异操作；4) 依此类推，直到满足程序结束的条件。

从计算复杂度角度看，假设目标函数个数为m、种群数为P、种群规模为N，NSGA算法需计算各种群的m个目标值，再通过冒泡排序法遍历整个种群对种群分级，其算法复杂度为O(mN3)。NSGA II为NSGA的改进算法，需要计算种群中支配个体p的个体数和被个体p支配的个体集合，该部分算法复杂度为O(mN2)；在排序部分应用快速非支配排序算法，其复杂度为O(N2)，因此，整个算法的计算复杂度为O(mN2)+O(N2)=O(mN2)。采用本文所提出的算法，1) 计算个体p的m个目标函数值，该部分复杂度为O(mN)；2) 根据种群P的各目标函数值确定各目标函数的最优解和最劣解，该部分复杂度为O(mN)；3) 根据各目标的最优解和最劣解计算个体p到正负理想解的距离，该部分复杂度为O(mN)。因此，整个算法的复杂度为O(mN)+O(mN)+O(mN)=O(mN)，有效降低了原有多目标算法的复杂度，相应实验见2.3节。

2 分区算法综合性能评估

算法测试包括3部分：初始化算法测试、合并算法测试、总体分区算法测试。其测试内容如下表1所示。

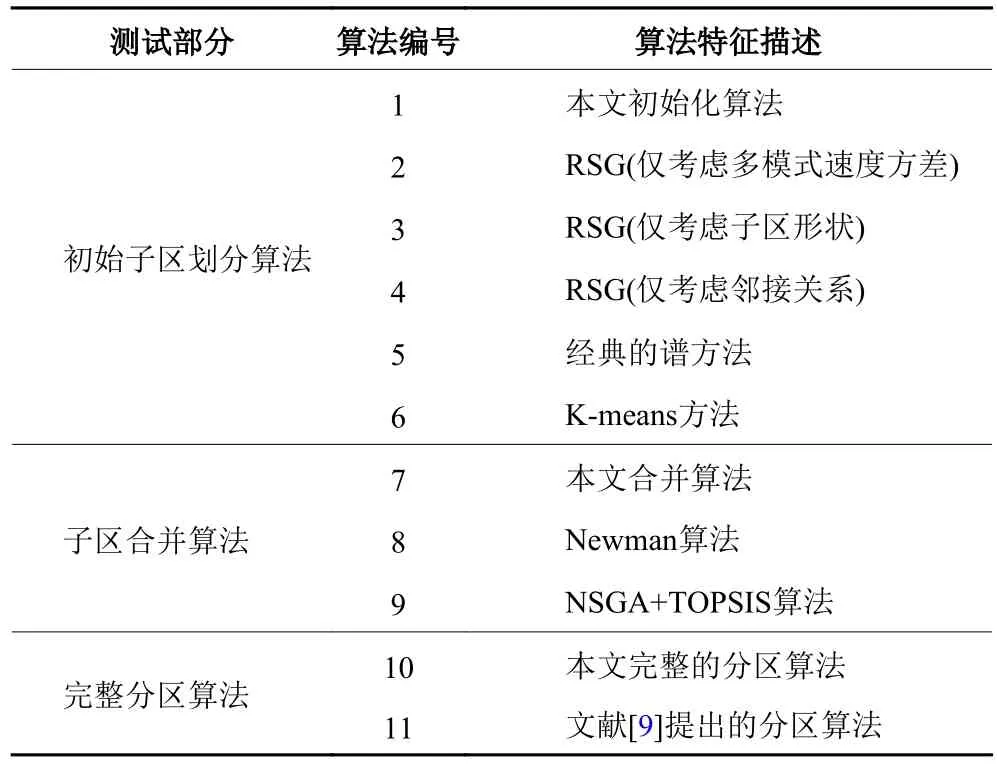
表1 算法测试实验设计Table 1 Algorithm test experiment design

2.1 分区性能评价指标

本文利用文献[9]所提出的两个评价指标(路段速度的加权总方差TV和子区之间的相似性指标NS)对不同分区结果进行评估。

以区域路段数作为权重计算分区路段速度的加权总方差TV，以评估该聚类算法的性能。

由于TV值是衡量算法整体性能的指标，并没有考虑区域之间的相似性。因此，增加另一个表示子区之间的相似性指标。

其中，uA和uB分别为区域A、区域B的速度均值。

由此可得到所有区域的平均相似性计算公式

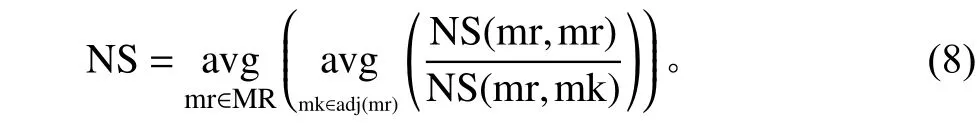
其中，mk为区域mr的邻接区域。

NS值越小，意味着各区域与其邻接区域的相似度越低，区域与区域之间的速度差异越大。区域之间相似度越低，意味着更容易识别速度较慢的拥堵区域和速度较快的通畅区域，得到离散度更低的多模式MFD图形，用于子区之间的边界控制，实现子区之间的交通流均衡控制。

2.2 初始子区划分算法测试

给定初始子区个数为6，利用6种算法分别对深圳罗湖区路网进行初始化。本文提出5个分区性能指标，利用TOPSIS方法对6种算法分区情况进行综合评价。表2所示结果表明，本文所提出的算法1初始化算法较优，其原因在于：1) 算法1相比较单模式RSG算法可以兼顾双模式性能指标；2) 算法1相较于算法5(谱方法)考虑了路段与区域的整体关系；3) 算法1相较于K-means算法考虑了路段的邻接关系。

2.3 子区合并算法测试

合并算法中各参数取值为：种群数量500、迭代次数300、交叉概率0.5、变异概率0.3，运算设备采用win10系统，AMD Ryzen 3 PRO 1300处理器(并行计算16线程)，8G内存。合并算法测试分为2部分：证明考虑子区整体方差关系的必要性(根据算法7与算法8的对比)；证明将排序规则带入多目标遗传的优化算法，要优于传统多目标优化方法(根据算法7与算法9的对比)。

图2表示在3种不同初始子区数量情况下，采用不同分区算法得到的2种交通流路网分区质量。如图2所示初始子区数越多，则分区结果质量越高，但也意味着组合方式越多。总体而言，算法7所得到的分区质量优于算法8，且这一优势随着子区数目的增加而更为明显。通过2种算法在不同子区数的比较可以看出，考虑区域内所有子区的方差在子区合并处理中十分必要。

传统多目标优化中，先利用NSGA算法求解Pareto最优解集，再建立排序规则选取最优解。本文算法的不同之处在于以排序规则建立虚拟适应度，以此进行优化计算。图3(a)表示2种方法在种群数2

000、迭代300次时的20次计算结果。可以看出，算法7多次迭代得到的最优解，基本到达了与算法9求解的Pareto端面，并且由于算法9方案Pareto最优解集的离散性，导致了利用TOPSIS算法得到的最优解很不稳定，其最优解的分布相对于算法7更为分散。说明本文算法在解迭代过程的稳定性上，优于传统多目标优化算法。

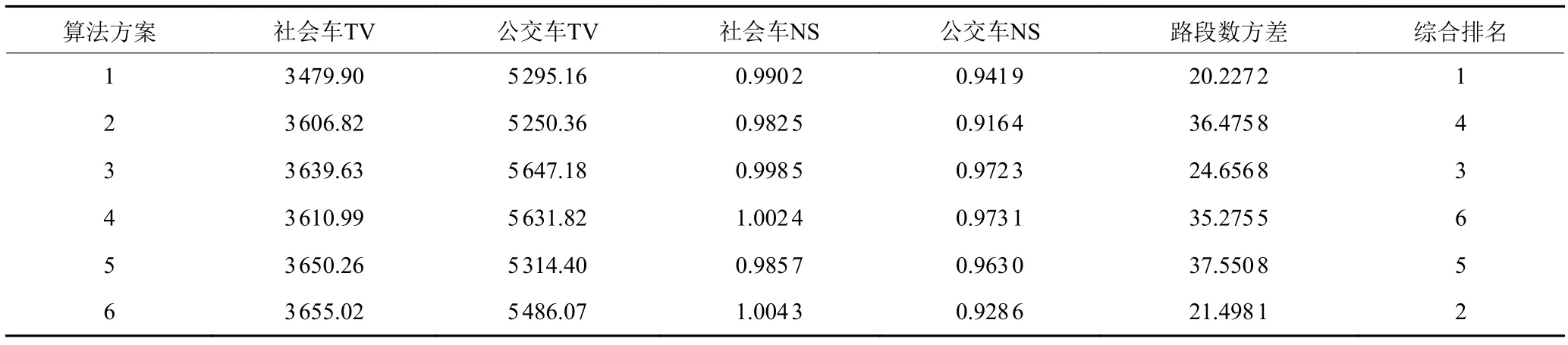
表2 初始化分区算法指标对比Table 2 Performance comparison for initialized partitioning algorithm

根据图3(b)，算法7的综合评价指数高于算法9，由此说明，算法7得到的最优解更接近2个优化目标的正理想解。图3(c)表明，算法7的计算效率明显胜于算法9，且耗时更加稳定。综上所述，本文算法在解的优良度、稳定性、计算效率上都明显胜于传统算法，可以高效处理多目标子区合并。

图2 考虑不同初始子区数的合并算法性能对比Figure 2 Comparison of merging algorithms 7 and 8

图3 基于算法7和9的分区性能指标对比Figure 3 Performances comparison using algorithms 7 and 9

2.4 整体多模式路网分区算法测试

本节利用算法10和11，分别对深圳市罗湖区路网进行分区测试。由于Ji等[9]的算法仅考虑单模式交通(社会车)，因此，在相似度矩阵构造过程中，考虑将路段的多模式速度进行加权分区。分区结果对比如图4所示，相应的性能指标对比如图5所示。

由图5(a)和(b)可知，对于从2～10个目标分区数的9种情形，算法10得到的社会车和公交车TV值全部优于算法11。由图5(c)和(d)可知，除了分区数为6、7、8的少数情形，算法10的社会车和公交车相似度指标基本优于算法11，说明算法10所得子区之间差异更为明显。

为确定最佳分区数，根据算法10得到的各分区数的社会车相似度和公交车相似度(如表3所示)，对于社会车来说，最佳分区数目为7个；对于公交车来说，则为5个。为同时考虑区域社会车和公交车的相似度，本文利用TOPSIS算法的综合评价指数(如表3所示)确定最优分区数量，因此，选取5作为最优分区数目。

3 实际路网中的经验多模式MFD识别

为探究分区算法用于识别多模式MFD的有效性，本文利用深圳市2016年5月24～26日的出租车GPS、固定检测器和公交车进出站数据，进行分析计算。具体包括13000辆出租车每隔1～30 s的GPS信息，数据量约为3000万条/d；53个道路断面的固定检测器流量数据，数据量约为800万条/d；578条公交线路的8 350辆公交车进出站记录，数据量约为500万条/d。

通常认为较为完整的子区多模式MFD图形，应包含路网出现单模式或多模式交通流量存在显著下降的情形，即区域社会车或公交车存在较为严重的拥堵情况。因此，根据图6所示分区结果，本文重点关注平均速度较低的子区3。该子区位于深圳福田区内，其中所包含的香蜜湖立交是连接深圳东西两侧的交通枢纽，与之连接的香蜜湖路是深圳市通勤日晚高峰最拥堵路段，该区域公交专用道占比约为26%。

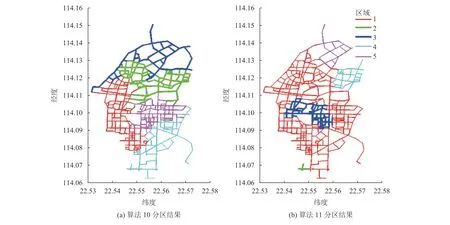
图4 算法10和11分区结果Figure 4 Partition results using algorithms 10 and 11

图5 算法10、11对比结果Figure 5 Comparison of algorithm 10 and 11

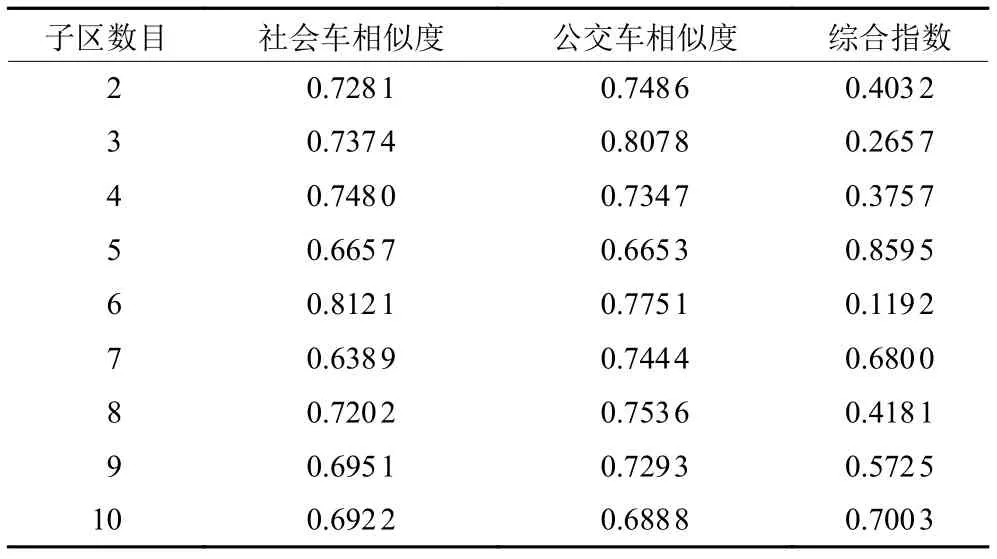
表3 算法10相似度指标Table 3 Similarity indices of algorithm 10

图7(a)中社会车的关键密度(区域流量最大时的车流密度)约为60 veh/km，此时社会车最高流量值约为1200 veh/h。随着车流密度继续增加至90 veh/km时，流量下降到1000 veh/h，意味着社会车已出现较为明显的拥堵，需要采取一定的交通控制手段以保证区域内车辆密度不再增加。图7(b)中公交车的关键密度约为4 veh/km，此时公交车最大流量值接近60 veh/h；随着公交车数量的继续增加，当公交车车辆密度达到5 veh/km时，流量下降至40 veh/km。需要说明的是，公交车MFD图形出现下降部分，并不意味着公交车的拥堵是由于公交车数量过多所导致，因为6 veh/km的公交车密度不足以使公交车产生拥堵。其拥堵的原因，更应该是社会车密度的增加，挤占了公交车的运行空间。这正是进行社会车与公交车交互关系研究的初衷，其中，多模式MFD是解释此交互关系的一种参考工具。

图6 深圳路网分区结果Figure 6 Partitioning result of Shenzhen road network

图7 子区3宏观基本图Figure 7 MFDs of subregion 3

多模式MFD分为车流MFD和乘客流MFD两类，两种MFD的横纵坐标均为社会车密度和公交车密度。车流MFD图形展示多模式路网中的所有车辆流量，其背景颜色代表两者车流量加权之和，颜色越深代表车流越高；乘客流MFD展示多模式路网中的所有乘客流量，小汽车乘客数通过车均载客系数进行折算，公交车通过实际刷卡数据推算得出车载乘客数，图形中的颜色深浅代表路网乘客流总数。

根据图8(a)可以看出，在车流最大时，社会车和公交车密度分别为80 veh/km和2～3 veh/km，但此时尚未达到最大乘客服务能力。由于公交车平均载客量更大，当图8(b)中的乘客流最大时，社会车和公交车密度分别为20 veh/km和3.0～4.5 veh/km，其公交车比例多于图8(a)。综上可得出以下结论：1) 在后续的交通控制研究中，可根据该多模式MFD，对给定区域内的社会车数量和公交车数量进行集成控制；2) 社会车和公交车的区域MFD难以识别到较为均匀的严重拥堵情况，由于拥堵时常存在方向性，可对区域内的路段分方向识别多模式MFD图形。

图8 区域3多模式MFD图形Figure 8 Multi-mode MFDs of subregion 3

4 结语

针对实际路网中多模式交通流并存的情况，提出考虑社会车速度与公交车速度的多模式大规模路网分区算法。相较于传统分区算法，本文算法考虑了路段与区域的整体方差关系和路网的多模式属性，并且在子区合并处理过程中提出TOPSIS与GA相结合的技术方案。利用深圳市路网和实际交通数据的分区实验证明：1) 本文所提出的初始化子区算法和合并子区算法的指标总体上优于传统分区算法；2) 整体算法的分区质量(TV)相比较已有分区算法的结果有大幅度提升；3) 根据本文分区结果和多源数据的处理结果，识别并证实了多模式MFD存在于现实路网中。