FSAE赛车整车建模及操纵稳定性仿真

张志亮，朱建军

（太原理工大学机械工程学院，山西 太原 030000）

1 引言

FSAE 系列赛事由 SAE（SocietyofAutomobileEngineering，美国汽车工程学会）主办，目的在于挑战世界各地大学生团队设想、设计、制造小型方程式赛车的能力[1]。该赛事自2010年引入中国后，很快受到国内高校的欢迎。由于大赛要求赛车的设计周期为1年，在这么短的周期内已不能采用传统设计开发的方法，而基于ADAMS/Car的整车虚拟样机仿真技术开始迅速的被国内外高校所采用，可以使研发人员在研发之初对整车进行虚拟仿真优化，达到缩短周期、降低成本的目的。由于赛车一般在高速工况下行驶，所以对整车的操纵稳定性要求比较苛刻，国内外学者对FSAE赛车的操纵稳定性也做了许多研究[2-5]。在国内参赛的高校中，FSAE赛车大多使用的是双横臂独立悬架，而使用的是自主设计的多连杆独立悬架，并创建了FSAE赛车整车模型，对多连杆独立悬架进行优化设计，建立优化前后两种车型，通过转向盘转角阶跃输入和虚拟蛇形穿越仿真试验对优化前后两种车型的操纵稳定性进行评价，对提升整车的操纵稳定性提供了参考，两种悬架结构简图，如图1、图2所示。

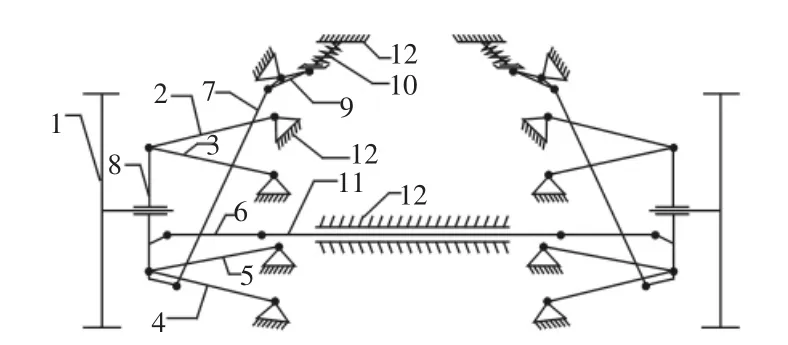
图1 双横臂独立悬架结构简图Fig.1 The Double Wishbone Independent Suspension Structure Diagram

图2 多连杆独立悬架结构简图Fig.2 The Multi-Link Independent Suspension Structure Diagram

2 整车模型建立

ADAMS/Car中模型的建立采用自下而上的方法，整个模型的建立需要三个阶段：模板文件-子系统文件-装配文件。ADAMS/Car建模最大的特点是不用考虑部件的几何形状，只需要正确建立各个部件的拓扑关系即可，但是为了模型的直观性，应尽可能将部件的几何体与实际相符。ADAMS/Car整车装配模型应包含前后悬架子系统、前后轮胎子系统、转向子系统、车身子系统、动力总成以及制动子系统。首先需要将各个子系统进行物理学抽象处理，然后根据CAD三维模型、实车测量数据、计算数据以及厂家提供的相关参数建立各子系统的模板文件，并创建通讯器将所有子系统连接通讯，最后将各个子系统与整车试验台组装，完成整车模型装配[6-7]。

2.1 悬架子系统建立

悬架包括前后上控制臂、前后下控制臂、转向节、推杆、转向横拉杆、摇臂、弹簧、减震器。各个部件的硬点坐标通过CATIA模型测量获得，部件之间通过相应的运动副连接，弹簧与减震器的参数通过厂家提供的参数分别建立属性文件。创建好的前悬架模型，如图3所示。

图3 前悬架子系统模型Fig.3 Front Suspension Subsystem Model

2.2 转向子系统建立

FSAE赛车采用的是无助力系统的机械式齿轮齿条转向系统，转向系统中各部件的硬点坐标同样通过CATIA三维模型测得，转向系统的相关参数通过定义参数变量来实现。

2.3 轮胎子系统建立

轮胎作为赛车与地面之间的直接接触部件，对于整车的操纵稳定性有着非常重要的作用。由于轮胎特性非常复杂，要想建立完全相同的物理模型较为困难，因此，一般都将轮胎用一组数学模型来表现。文中FSAE赛车采用的是ADAMS/Car中的pac89魔术轮胎模型[8]。建立轮胎属性文件时只需要将使用的HOOSIER轮胎的相关参数在pac89轮胎模型的属性文件中修改即可。

2.4 动力总成及制动系统建立

动力系统在ADAMS/Car中的功能是提供车轮驱动转矩，所以不需要按实际机械结构详细建模，而是将发动机、变速器、离合器三个功能集中在一个模板中，使用函数模拟实现各部分的功能。发动机特性曲面参数由外部属性文件提供，变速器档位由样条控制，发动机与离合器由一个状态方程完成。制动系统是一个简化的制动系模板，制动钳和制动盘通过输入通讯器分别与转向节与车轮相连，制动力由两者之间的一个单作用力矩定义。

2.5 整车模型装配

通过上述创建好的各个子系统，在ADAMS/Car中通过通讯器进行通讯，完成整车模型装配。装配好的整车模型，如图4所示。

图4 整车虚拟样机Fig.4 Vehicle Virtual Prototype

3 悬架系统优化

悬架作为轮胎和车身之间的传力部件，对整车的操纵稳定性有着非常重要的作用。为了改善FSAE赛车的整车操纵稳定性，就必须改善悬架的运动特性。

3.1 前悬架运动特性优化仿真

根据上述所建立的前悬架和转向子系统，通过通讯器与悬架试验台进行连接，建立前悬架与转向系统模型。在仿真之前，应将悬架的主销参数设定好，根据创建的前悬架与转向虚拟样机进行双轮同向激振仿真试验，因大赛规则要求车轮上下跳动量应大于一英寸（25.4mm），故设定其上下跳动量为（±30）mm。

应用ADAMS/Insight模块对悬架双轮同向激振仿真试验进行多目标优化。首先运行一次双轮同向激振仿真试验，然后依据结果进行DOE目标参数的设定，目标参数选择优化中的最大绝对值，将设定的目标参数在ADAMS/Insight模块进行输出，并进行设计变量及其约束条件的设定，选择优化分析方法对目标参数进行优化[9]。文中选取的目标参数是前束角、外倾角、内倾角及后倾角。考虑到轮辋的空间限制，以及转向立柱的加工难度，悬架控制臂的外硬点坐标不宜变动，设计变量选择上下控制臂及横拉杆的内硬点的Y、Z坐标，由于其他部件的定位及考虑到整车的布置，硬点坐标不能变化太大，范围选择（±10）mm。设计规范分别选择试验设计响应面，交互式和全因子法，执行1024次迭代仿真。考虑到多目标优化之间的影响，通过ADAMS/Insight模块里的Optimize模块进行多目标优化。优化分析方法选择平方和加权法，目标值设定为1024次迭代仿真中的最小值，由于四个参数对整车的操纵稳定性的影响程度相当，选择每个目标参数的加权系数为0.25[10]。运行之后得到优化前后各设计变量的硬点坐标，如表1所示。

表1 优化前后的各硬点坐标Tab.1 The Hard Point Coordinates Before and After Optimization

3.2 优化结果分析

根据优化后的硬点坐标更改悬架系统的硬点坐标，再次运行双轮同向激振仿真试验，得到优化前后的前束角、外倾角、内倾角、后倾角的变化曲线，如图5～图8所示。

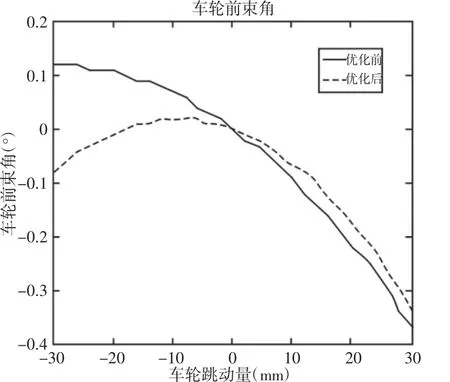
图5 前束角变化曲线Fig.5 The Changing Curve of the Toe Angle

图6 外倾角变化曲线Fig.6 The Changing Curve of the Camber Angle

由图5可知，在车轮跳动量（±30）mm行程内，优化后的前束角的变化范围为0.36°，较优化前的前束角变化范围0.49°减少了0.13°，优化效果不是很明显，但是前束角的变化范围已经很小，且前束角在车轮上跳过程中保持负值变化，故优化结果可以接受。

由图6可知，多连杆独立悬架优化前后外倾角的变化趋势保持不变，优化前在车轮上跳过程中最大为1.01°，下跳过程中最大为0.92°，外倾角的变化量为1.93°；优化后在车轮上跳过程中最大为0.53°，下跳过程中最大为0.44°，外倾角的变化量由之前的1.93°降为0.97°，优化效果非常显著。

图7 后倾角变化曲线Fig.7 The Changing Curve of the Caster Angle

由图7可知，多连杆独立悬架主销后倾角在车轮上跳极限达到最大值5.43°，下跳极限达到最小值1.79°，主销后倾角的变化量为3.64°，变化量很大，需要优化。经优化后主销后倾角保持原有变化趋势，最小值达到2.94°，最大值4.46°，变化量为1.52°，优化效果非常显著。由图8可知，多连杆独立悬架主销内倾角在上跳极限达到最大值8.31°，下跳极限达到最小值6.23°，后倾角的变化量为2.08°，需要优化。经优化后主销内倾角保持原有变化趋势，最小值达到6.63°，最大值为7.72°，变化量为1.09°，优化效果非常显著。

图8 内倾角变化曲线Fig.8 The Changing Curve of the Kingpin Inclination Angle

4 整车操纵稳定性仿真

4.1 转向盘转角阶跃输入仿真

参照国标GB/T 6323-2014[11]，给方向盘一个转角阶跃形式的角度输入，通过横摆角速度评价汽车的瞬态响应。首先让赛车在给定的初速度下匀速直线行驶达到一个稳定状态，然后突然输入一个方向盘转角，转角的输入时间应在0.2s以内。转角输入后保持一段时间使赛车转向行驶，直至其达到另一个稳定状态。文中赛车最高车速为120km/h，按照国标的要求，试验车速应取赛车最高车速的70%且四舍五入为10的整数倍，故试验车速应选择80km/h。输入的方向盘转角应使赛车达到稳态时的侧向加速度为（1～3）m/s2，通过多次仿真试验得到赛车达到稳态时的侧向加速度为2m/s2的方向盘转角。通过ADAMS/Car中开环转向仿真试验下的Step Steer仿真试验进行仿真，输入初始条件后运行仿真得到优化前后车型的仿真结果，如图9所示。

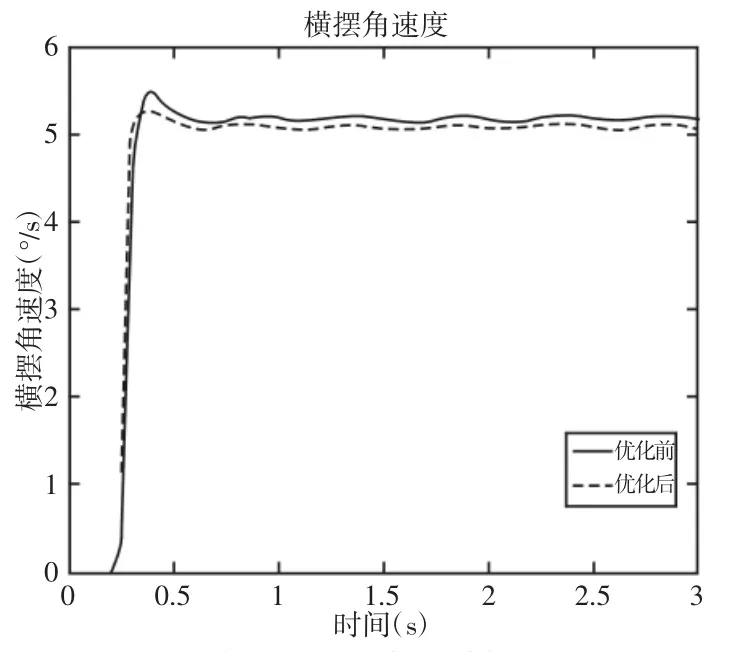
图9 优化前后整车的瞬态响应Fig.9 The Vehicle Transient Response Before and After Optimization

根据图9可得优化前后两种车型的转向盘转角阶跃输入仿真的评价指标，如表2所示。转向盘转角阶跃输入试验的评价计分值NJ由公式（1）计算：

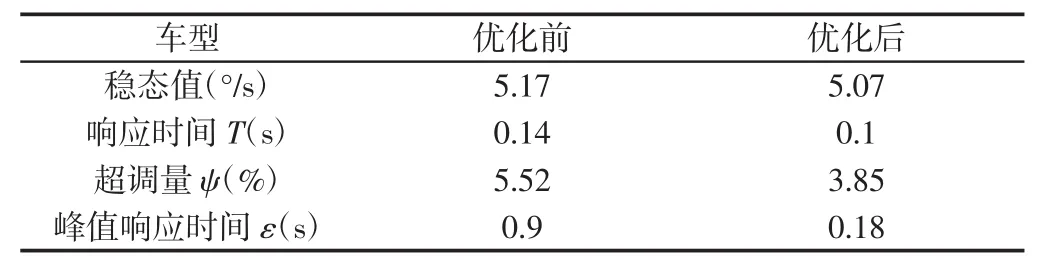
表2 优化前后角阶跃输入仿真评价指标Tab.2 The Evaluation Index of the Step Steer Test Before and After Optimization

式中：NJ—转向盘转角阶跃输入试验的评价计分值；T、T60、T100—横摆角速度响应时间及其上下限值。

表3 优化前后转向盘角阶跃输入仿真试验综合评价计分值Tab.3 Comprehensive Evaluation Score of the Step Steer Test Before and After Optimization

当赛车的最大速度不大于120km/h时，T60取0.2s，T100取0.06s。由公式可计算出优化前后两种车型转向盘转角阶跃输入仿真试验综合评价计分值NJ，如表3所示。由表3可知，优化前后的综合评价得分都大于国标规定的70分，且优化后较优化前有明显提升，优化效果显著。

4.2 虚拟蛇形穿越仿真试验

参照国标GB/T 6323-2014的试验方法，使赛车在一定长度的标杆之间进行蛇形穿越，通过赛车蛇形穿越过程中的横摆角速度、转向盘转角等进行评价。

由于ADAMS/car标准模板中没有蛇形穿越的行驶路径和驾驶控制文件，需要通过ADAMS/car中的事件发生器按照国标要求编写蛇形穿越的行驶路径和驾驶控制文件，之后通过ADAMS/car中的驱动控制文件仿真模块按照不同的初始速度进行蛇形穿越仿真试验。根据比赛中速度的统计结果依次进行了初速度为（10～18）m/s2的9次仿真试验，仿真时首先让赛车直线行驶，直至其达到初始速度的稳定状态后，然后开始蛇形穿越仿真试验。通过对优化前后两种车型进行虚拟蛇形穿越仿真试验得到结果，如图10～图11所示。

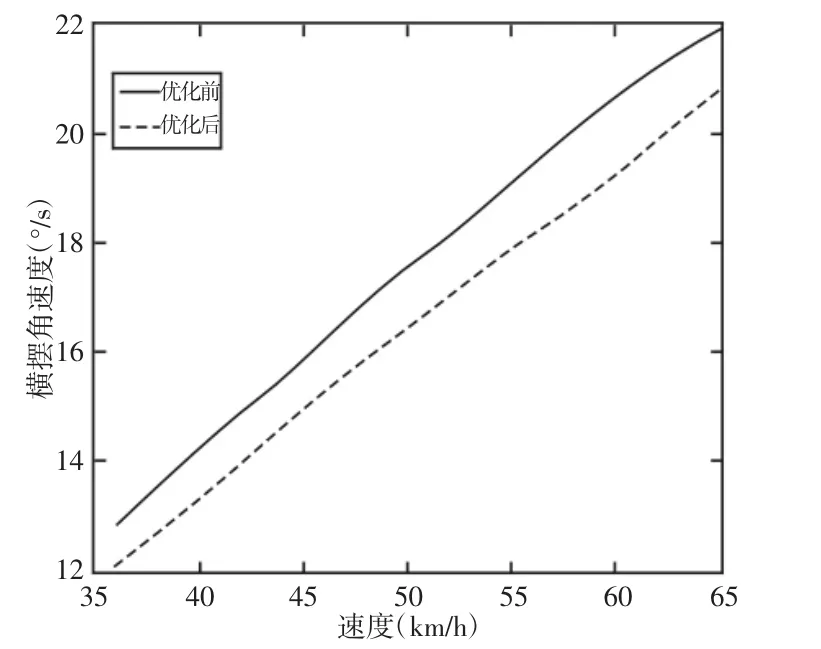
图10 优化前后平均横摆角速度随车速的变化曲线Fig.10 The Changing Curve of Average Yaw Rate with the Speed

图11 优化前后平均转向盘转角随车速的变化曲线Fig.11 The Changing Curve of Average Steering Wheel Angle with the Speed

按照QC/T480-1999[12]对蛇形仿真试验进行评价。平均横摆角速度峰值评价计分值Nr由式（2）计算。

式中：Nr—平均横摆角速度峰值评价计分值；r、r60、r100—初始速度为65km/h时，汽车平均横摆角速度峰值及其上下限值。平均转向盘转角峰值评价计分值Nθ由式（3）计算。

式中：N兹—平均转向盘转角峰值评价计分值；兹、兹60、兹100—初始速度为65km/h时，汽车平均转向盘转角峰值及其上下限值。虚拟蛇形穿越试验的评价计分值Ns由式（4）计算：

式中：Ns—虚拟蛇形穿越试验的评价计分值。

表4 优化前后虚拟蛇形穿越仿真试验综合评价计分值Tab.4 Comprehensive Evaluation Score of the Fish Hook Test Before and After Optimization

根据图 10～图 11和标准 QC/T480-1999由式（2）～式（4）可计算出优化前后转向盘转角阶跃输入试验综合评价计分值，如表4所示。由表4可知，优化前后两种车型虚拟蛇形穿越仿真试验的综合评价计分值都大于国标规定的60分，且优化后较优化前有所提升。

5 结论

（1）基于自主设计的多连杆独立悬架创建了FSAE赛车各个子系统与整车虚拟样机。

（2）以多连杆独立悬架的主销内倾角、主销后倾角、外倾角、前束角为优化目标，运用ADAMS/Insight模块对设计变量做了灵敏度分析，并进行了多目标优化分析，优化后悬架的主销内倾角、主销后倾角、外倾角、前束角变化范围明显减小。主销内倾角、主销后倾角变化范围的减小可以使赛车转向时的回正力矩保持在一个适中的范围内，可以提高车手对赛车的操控性；外倾角、前束角变化范围的减小可以保证赛车稳定的直线行驶，有利于提升赛车的行驶稳定性。

（3）通过对优化前后两种车型进行整车转向盘转角阶跃输入与虚拟蛇形穿越仿真试验，并对整车操纵稳定性进行评价。得出优化前后两种车型转向盘转角阶跃输入仿真试验得分分别为77分、88分，虚拟蛇形穿越仿真试验得分分别为82.1分、84.3分。由此可知，通过对多连杆悬架的优化达到了整车操纵稳定性的提高，对整车操纵稳定的提升提供了参考。