变刚度横置板簧式悬架系统设计研究

王孝鹏

（1.三明学院机电工程学院，福建 三明 365004；2.机械现代设计制造技术福建省高校工程研究中心，福建 三明 365004）

1 引言

FSAE赛车的设计关注的重点是整车的操控稳定性，操稳性对整车的底盘要求较高。纵观国内近些年赛事，绝大多数FSAE赛车前后悬架均采用推杆式双横臂悬架，有少数车辆采用双横臂悬架。推杆式悬架与双横臂臂悬架对于整车稳定的提升均有改善作用，但推杆式悬架最大的缺点是安装时需要占用较大的车身空间。FSAE赛车驱动采用中置后驱模式，发动机、传动系统、车身附属装置及悬架系统均布置在后轮附近空间，集成度较高，同时导致整车质心后移，稳定性变差；针对此问题提出横置板簧悬架模型设计，旨在去掉推杆及螺旋弹簧部件，减少空间占用，同时车轮及非簧载质量减轻，固有频率提升，车辆振动减小；横置板簧悬架研究文献较少，文献[1]指出横置板簧实际上为单侧弹力连杆，对悬架系统的静动力学都存在影响，对改善悬架系统的侧向与纵向特性有明显作用，但并没有系统考虑整车弯道行驶模式下其特性；文献[2-3]采用仿真与实验结合的方式验证了横置板簧悬架四轮定位参数随车轮的变化状态，指出轮距，外倾角与前束角变化理想，占用空间小，结构紧凑等优点，但文献也没有从整车角度去衡量横置板簧悬架的特性；横置板簧即起到螺旋弹簧作用同时又起到横向拉杆作用[4-6]。在横置板簧悬架模型的基础上，通过改变板簧与车身的固定位置既可以改变板簧横向力臂，最终可以分段调节板簧的刚度特性，板簧两端与下控制臂连接，安装在悬架最底部，不占用空间，可以进步一步降低整车质心高度，对于提升操控稳定性极为有利。

2 横置板簧悬架

国内FSAE赛车前后悬架均为推杆式双A臂悬架模型，此悬架的优点是悬架空气动力学性能较好，阻尼效率高，缺点是悬架的整体质量增幅较大，占用较多的安装空间。FSAE赛车为中后置后轮驱动，后悬架附近需要安装发动机、变速器、传动机构及悬架等附属装置，系统部件布置空间小且后轴系偏中；针对此问题提出一种横置板簧悬架模型设计，增大后轴布置空间，降低车身质心，进一步提升整车稳定性。

2.1 变刚度板簧模型

变刚度板簧模型，如图1所示。钢板宽度为20mm，厚度为5毫米，长度为730mm；板簧长度中心线上设计出9个孔，孔直径为5mm，此板簧有4种刚度：RP-5为板簧长度的中心，固定RP-5时，单侧臂RP-5与RP-1之间的刚度为A，单侧臂RP-5与RP-9之间的刚度为A；RP-4与RP-6关于RP-5对称，固定RP-4与RP-6时，单侧臂RP-4与RP-1之间的刚度为B，单侧臂RP-6与RP-9之间的刚度为B；RP-3与RP-7关于RP-5对称，固定RP-4与RP-6时，单侧臂RP-3与RP-1之间的刚度为C，单侧臂RP-7与RP-9之间的刚度为C；RP-2与RP-8关于RP-5对称，固定RP-2与RP-8时，单侧臂RP-2与RP-1之间的刚度为D，单侧臂RP-8与RP-9之间的刚度为D；RP-1与RP-9与下控制臂刚性固定连接。

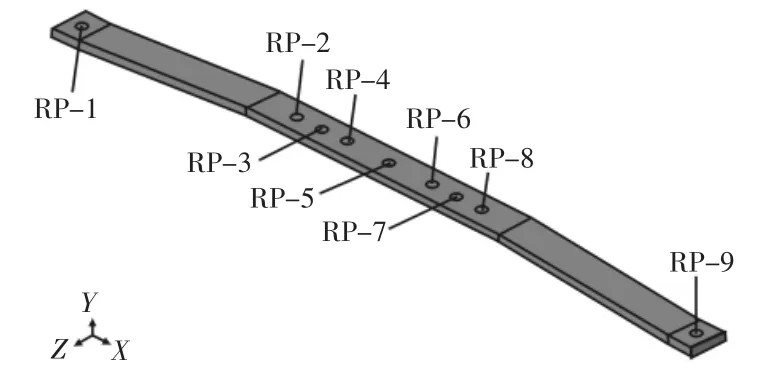
图1 变刚度板簧模型Fig.1 Variable Stiffness Leafspring Model

2.2 板簧模态

在ABAQUS软件中计算板簧前20阶模态并输出板簧中性模态文件MNF到ADAMS软件总构建横置板簧悬架模型。在RP-1至RP-9孔中分别建立MPC多点约束，输出模态中固定约束RP-1、RP-5、RP-9；网格划分为六面体，共2808个单元，单元类型C3D8R；计算并生成子数据块，其中，5、6、7阶模态，如图2～图4所示。

图2 五阶模态Fig.2 Fifth Order Mode

图3 六阶模态Fig.3 Sixth Order Mode

图4 七阶模态Fig.4 Seventh Order Mode

2.3 板簧刚度

板簧子数据块完成计算后通过转换命令生成板簧中性文件MNF，在ADAMS中导入中性文件添加约束、驱动计算板簧刚度，单侧臂刚度测试过程如下：RP-9处添加与Y轴平行的移动副，在移动副上添加驱动位移，每秒运动20mm，分别固定约束RP-5、RP-6、RP-7、RP-8 计算出刚度 A、B、C、D，如图5所示。刚度 A为26.10N/mm、刚度B为56.04N/mm、刚度C为107.54N/mm、刚度D为232.55N/mm。从计算结果可以看出，同一片钢板弹簧，通过改变力臂大小，刚度实现了约9倍范围内变化。

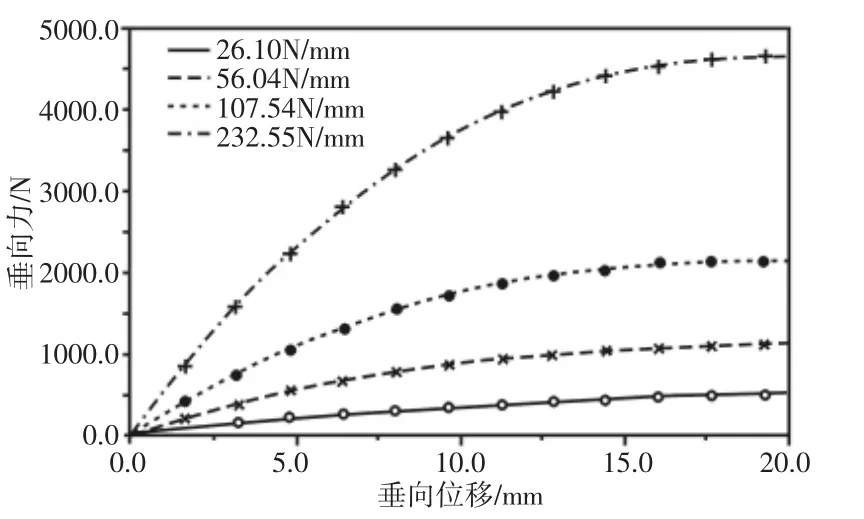
图5 板簧刚度Fig.5 Leafspring Stiffness

2.4 参数测试

前横置板簧悬架模型前束角设置为1°，车轮外倾设置为-5°，外倾角为负且角度较大有利于提升整车稳定性；对前横置板簧悬架模型进行同向车轮激振实验，车轮跳动距离为50mm，计算出推杆式双横臂悬架与横置板簧悬架的前束角变化范围分别为（-1.17～2.85）；（-1.30～2.75）；车轮外倾角变化范围分别为（-2.53～-7.83）；（-2.57～-7.90）；主销内倾角变化范围分别为（12.66～17.97）；（12.70～18.04）；主销后倾角变化范围分别为（0.0049～0.0843）；（-0.01～6.8e-5）；从计算结果可以看出：前束角、外倾角、内倾角曲线重合度较高，主销后倾角变化角度小，但相对变化范围较大，变化趋势，如图6所示。横置板簧悬架模型后倾角在车轮跳动中变化范围不大，性能相对推杆式双横臂悬架有所提升。

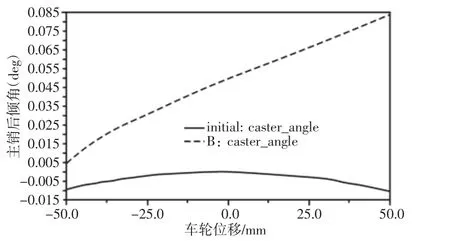
图6 主销后倾角Fig.6 Kingpin Back Angle

3 定常半径弯道仿真

用前后横置板簧悬架模型完成FSAE整车模型建立，如图7所示。整车共196个自由度。前后横置板簧均有A、B、C、D四种刚度，通过前后悬架刚度组合共有16组刚度可调，刚度组合，如表1所示。表中：G1—前轴悬架板簧刚度；G2—后轴板簧刚度。板簧刚度C、D相对于刚度A大很多，接近于刚性连接，同时由于后悬架刚度相对于前悬架刚度一般会略大或者相同，在表1刚度组合表中，具有实际研究意义的刚度组合为AA、BA、BB、CC、DD；如果变刚度板簧的刚度增量变化较小，表中16中刚度组合均具有研究意义。AA、BA、BB、CC、DD五种刚度组合组合中，AA组合整车静平衡发散，原因在于后悬架板簧刚度为A时变形量过大导致，BA、BB两种刚度组合计算结果相近，说明后轴刚度对整车稳定性具有主导作用，因此选取BB、CC、DD三种刚度组合与采用推杆式悬架FSAE整车进行对比分析。对整车进行定常值半径转弯仿真，相同工况下测试整车横摆角速度，侧向加速度稳定性参数，车辆转向半径为15m，初始速度为10km/h，最终速度为50km/h，发动机变速器均为为3档工况，运行时间10s。

图7 横置板簧整车模型Fig.7 Horizontal Plate Spring Vehicle Model

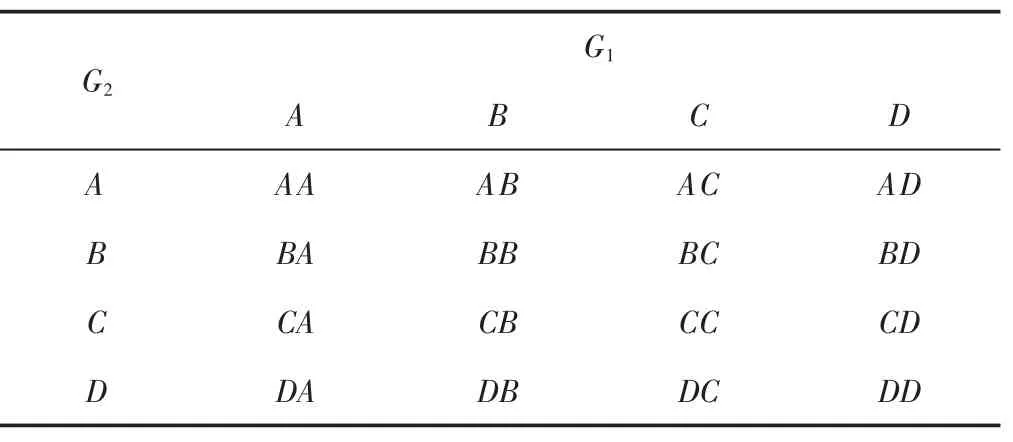
表1 刚度组合表Tab.1 Stiffness Combination Table

图8 车身高度Fig.8 Body Height

图10 侧向加速度Fig.10 Lateral Acceleration

图形中initial曲线表示推杆式双横臂悬架FSAE整车模型计算结果。图8中看以看出，推杆式双横臂悬架整车模型车身高度为348.17mm，采用横置板簧悬架后整车的车身高均有降低，，BB刚度组合后车身高度为302.75mm，降低45.42mm；CC组合后车身高度为310.88mm，降低37.29mm；采用DD组合后车身高度为314.37mm，降低33.8mm；横摆角的速度变化曲线，如图9所示。initial为29.39deg/s；BB刚度组合最大值为24.50deg/s，性能提升16.64%；CC刚度组合最大值为26.65deg/s，性能提升9.32%；DD刚度组合最大值为27.48deg/s，性能提升6.50%；侧向加速度，如图10所示。initial为（-0.40）mm/s2；BB 刚度组合最大值为（-0.28）mm/s2，性能提升30.00%；CC刚度组合最大值为（-0.33）mm/s2，性能提升17.50%；DD刚度组合最大值为（-0.35）mm/s2，性能提升12.50%。

4 板簧优化

通过定值半径转弯计算，采用横置板簧悬架的整车稳定性均具有提升，其中BB刚度组合的整车性能最佳。但BB、CC刚度组合在实验初始都伴有较大的震荡现象，针对此问题对板簧进行继续优化。

4.1 板簧衬套

针对实验初期存在的震荡现象，当刚度组合为BB时，在板簧孔RP-4、RP-6与RP-1、RP-9处添加柔性衬套；当刚度组合为CC时，在板簧孔RP-3、RP-7与RP-1、RP-9处添加柔性衬套；刚度组合为CC时添加衬套，如图11所示。

图11 横置板簧衬套Fig.11 Transverse Leafspring Bushing

对优化后的横置板簧悬架整车模型进行计算，当刚度组合为CC时，图12中显示整车实验初期震荡现象改善明显，同时稳定性指标参数进一步提升，其中横摆角度最大值降低为25.44deg/s，性能相对添加衬套前提升4.54%，相对于推杆式双横臂悬架提升13.44%；侧向加速度最大降低为（-0.30）mm/s2，性能相对添加衬套前提升9.10%，相对于推杆式双横臂悬架提升25.00%；当刚度组合为BB时，图13中显示整车稳定性指标参数进一步提升，其中横摆角度最大值降低为18.99deg/s，性能相对添加衬套前提升22.49%，相对于推杆式双横臂悬架提升35.39%；侧向加速度最大降低为（-0.17）mm/s2，性能相对添加衬套前提升39.29%，相对于推杆式双横臂悬架提升57.50%；车身高度降低为266.99mm，相对于推杆式悬架整车模型整车降低81.18mm。

图12 稳定性参数/CCFig.12 Stability Parameter/CC

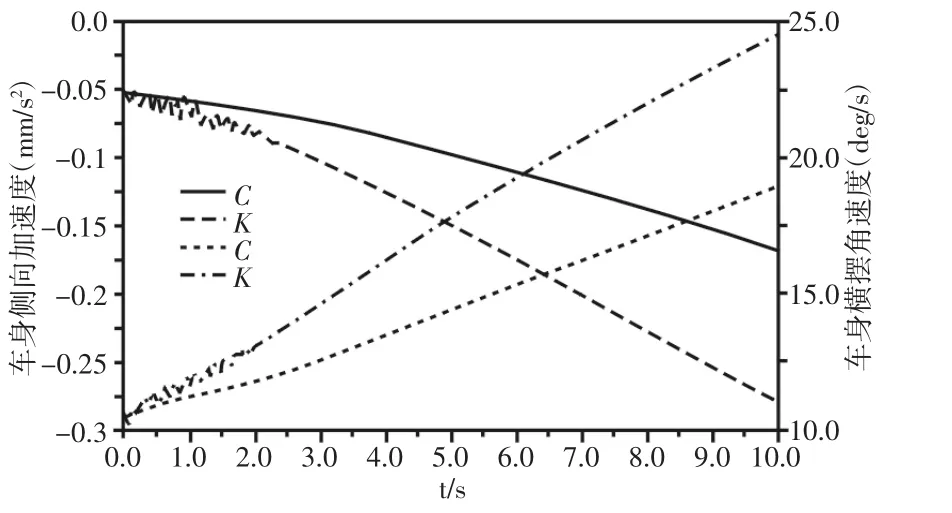
图13 稳定性参数/BBFig.13 Stability Parameter/BB

4.2 板簧轻量化

对FSAE赛车右后轮处板簧与下控制臂连接点测量受力，如图14所示。

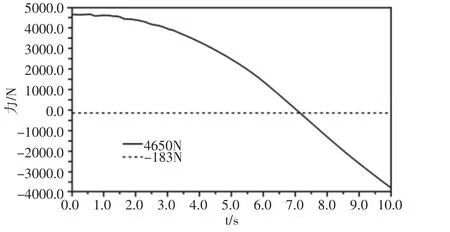
图14 右后轮RP-1点受力Fig.14 Right Rear Wheel RP-1 Point Force

其中，侧向力最大为4650N，垂向力为183N；板簧纵向力微小可以忽略，从计算结果可以看出横置板簧主要承受侧向力与垂向力，其作用相当于在悬架上增加了一根横向拉杆同时起到弹簧作用，这也是采用横置板簧悬架整车模型弯道模式下侧向加速度参数大幅降低的最主要原因，整车纵向力主要由悬架上下控制臂承受。横置板簧材料：60Si2Mn，弹性模量：2.06E5兆帕，泊桑比：0.29，密度：7.74E-9吨每立方毫米；抗拉强度1270兆帕。对板簧进行有限元分析，单侧臂应力变化，如图15所示。最大应力为449.7兆帕，最大应变为28.3mm。图中颜色区域承受应力较小，远小于抗拉强度，对此区域进行拓扑优化；创建拓扑优化任务，确定目标函数，使应变能最小化；创建约束条件，约束RP-1与RP-9与参考点Y方向绝对值，使最大化位移不超过28mm；约束体积为初始体积的80%；约束选择优化区域前需要先对板簧进行切割，冻结板簧边缘区域，防止优化过程中出现板簧几何体不连续现象；提交计算后循环计算30次，输出优化后的拓扑模型，如图16所示。

图15 单侧板簧应力Fig.15 One-Sided Leafspring Stress

图16 板簧拓扑几何模型Fig.16 Leafspring Topology Geometry Model

图17 优化后单侧板簧应力Fig.17 Optimized One-Sided Leaf Spring Stress

图18 优化后板簧刚度Fig.18 Optimized Leafspring Stiffness

在拓扑优化几何模型的基础上理想化板簧单侧几何体[7-10]，如图17所示。对优化后的板簧再次进行分析，约束与载荷条件相同，计算结果显示最大应力为555.90兆帕，最大应变为28.10mm，与优化之前对比最大应力增加，最大应变减小，最大应力依然小于抗拉强度，符合设计要求。优化前横置板簧质量为0.5957kg，优化后质量为0.4527kg，质量减少24.0%，优化效果较明显；对优化后的板簧进行刚度测试，计算显示优化后的板簧刚度为50.65N/mm，如图18所示。相对优化前刚度56.04N/mm有所减小；横置板簧替换后通过仿真实验计算整车稳定性参数，如图19所示。整车侧向加速度与横摆角速度分别为：0.1577mm/s2、18.32deg/s，性能相对优化前整车BB刚度组合提升：8.05%、4.58%，但运行过程中伴有微小震荡现象。

图19 优化后稳定性参数Fig.19 Optimized Stability Parameter

5 总结

（1）变刚度横置板簧可以实现弹簧刚度在9倍范围内变化，最小刚度为26.10N/mm，最大刚度为232.55N/mm，FSAE整车模型可以实现16种可变刚度组合底盘模型；（2）FSAE采用横置板簧后，相对于推杆式双横臂悬架整车车身高度均有所降低，侧向加速度、横摆角速度等稳定性参数均提升，其中BB刚度组合性能提升最为明显，分别为16.64%、30.00%；（3）横置板簧与下控制臂、车身连接处添加柔性衬套后，仿真初期震荡现象改善明显，同时整车稳定性指标进一步提升，车身高度总降低81.18mm；（4）板簧结构优化后，质量减少24%，FSAE整车稳定性继续改善，但伴有震荡现象。