考虑啮合刚度时变性的齿轮传递误差计算

谭学飞，鲁文佳，张义民，赵燕辉

（1.东北大学机械工程与自动化学院，辽宁 沈阳 110819；2.沈阳化工大学机械工程学院，辽宁 沈阳 110142）

1 引言

齿轮传动系统的激励因素主要包括电机扭矩和负载扭矩两大外部激励，同时受到啮合刚度、齿轮传递误差、啮合冲击等内部激励的影响。轮齿啮合刚度和传递误差对齿轮转子系统的振动特性和动力学性能产生不容忽视的巨大影响[1-2]。

齿轮传递误差是指从动齿轮实际啮合位置与理论齿廓无变形啮合位置的偏差，文献[3]指出齿轮传递误差与齿轮制造精度，安装精度和齿轮修形工艺有着密不可分的联系，文献[4]运用试验方法测量了齿轮静态传递误差和齿轮啮合刚度；文献[5]根据传递误差来源与影响因素，利用啮合轮齿几何关系建立了传递误差与不同影响参数的数学关系。国内外学者对啮合刚度和传递误差的关联性以及齿轮修形对传递误差的影响方面进行了相应研究，文献[6]采用有限元方法对齿轮轴所在的有限单元加载，外载作用于齿轮安装轴进而引起啮合齿轮副的相对变形和轮齿啮合误差的加剧；文献[7-10]均通过有限元法模拟轮齿啮合副的啮合作用，轮齿有限元接触加入了齿轮修型因素进而模拟其对齿轮传递误差的影响。文献[11-12]运用有限元方法分析轮齿修形和齿轮传递误差的关系，进而建立了考虑齿轮修形量的齿轮转子振动模型并研究了其对系统动态响应的影响。

由于齿轮传递误差的形成原因的复杂性，关于时变刚度和传递误差关联性的分析多通过有限元分析方法，建模过程复杂且缺乏通用性。为充分揭示两者的内在联系，同时考虑轮齿修形工艺对传递误差的影响，准确给出了齿顶修形量对齿轮啮合区的影响区间模型以及齿向修形模型，建立了考虑齿轮修形因素的基于时变啮合刚度的齿轮传递误差计算模型。

2 齿轮时变啮合刚度模型

2.1 直齿轮轮齿模型

直齿轮轮齿的端面是一个变截面悬臂梁，其模型，如图1所示。

图中：F—垂直于齿轮的作用力；h—啮合力作用位置处齿厚的一半；φ1—啮合力方向与齿厚方向的夹角；rb—基圆半径；d—轮齿在外力的作用下有效储存能量的长度，即啮合力作用点到齿根圆固定部分的距离，dx、2hx—微元截面的宽度与长度。

2.2 时变啮合刚度算法

轮齿在外载荷的作用下齿轮啮合副产生弹性变形进而形成赫兹接触能量、弯曲能量、剪切能量、径向压缩能量和存在于齿基的能量，可以通过能量法来计算刚度[13-15]。根据文献[1]可得齿轮副单齿啮合刚度K：

式中：Kh—赫兹接触刚度；Kbi—齿轮弯曲刚度；Ksi—齿轮剪切刚度；Kai—径向压缩刚度；Kfi—齿基刚度。

图1 直齿轮轮齿悬臂梁模型Fig.1 Cantilever Beam Model of Spur Gear Tooth

式中：E—材料的弹性模型；ν—材料泊松比；b—齿宽。

根据文献[16]可得到齿轮齿基刚度表达式（参数具体数值详见文献[16]）：

3 齿轮变刚度传递误差模型

3.1 变刚度传递误差计算方法

考虑齿轮的弹性变形，受力偏载和齿轮修形等因素，齿轮传递误差可以表示为[17]：

式中：e（t）—齿轮传递误差；pa（t）—齿顶修形；cm（t）—齿向修形；

bd（t）—齿轮弹性变形；ma（t）—啮合齿对的受力偏载变形。

基于这里研究重点，不考虑受力偏载的影响。

进而可以得到齿轮啮合产生的弹性变形：

由理论力学和弹性力学可知沿啮合线的啮合力F（t）可通过以下公式计算得出：

式中：rb—齿轮基圆半径；T（t）—齿轮的时变负载，在恒定扭矩情况可近似为常量；K（t）—齿轮的时变啮合刚度。

由式（1），式（9）可知，当已知负载T时，可求得齿轮弹性变形bd，进而由式（8）可知，当给定齿轮修形量即可得到基于时变刚度的周期性时变传递误差。并将齿轮传递误差以啮合频率进行傅里叶级数展开：

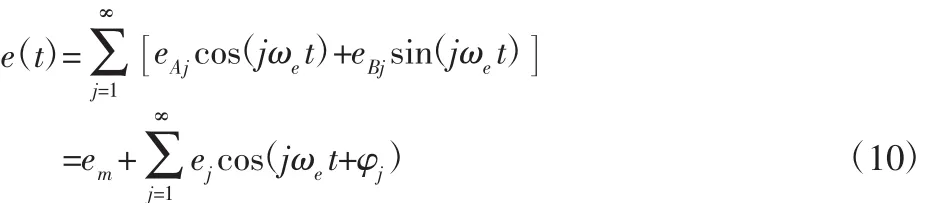
下面将给出齿顶修形量和齿向修形量计算模型。

3.2 齿顶修形误差计算模型

齿轮齿顶修形有多种修形曲线，拟采用如图2所示的直线修形方式，其表达式为：

式中：Ca—齿顶修形量；La—修形长度；x—变量表示不同齿廓位置的修形量。

图2 齿轮齿顶修形Fig.2 The Tooth Tip Modification of the Gear

根据齿轮的啮合方式可知，齿轮的啮合以主动轮的齿根推动从动轮的齿顶开始，以主动轮的齿顶与啮合线相交为止，分析可知齿顶部分参与齿轮啮合的啮入、啮出过程，而在齿轮转过一个基圆齿距的啮合过程，齿轮的啮入、啮出发生在双齿啮合区，即齿轮齿顶修形产生的修形误差发生于双齿啮合区的对称两端，对单齿啮合区没有影响。

重点介绍齿顶修形在双齿啮合区的影响区间，以确定齿顶修形误差在啮合周期的具体影响区间。根据图1几何关系可建立方程：

式中：γM—轮齿中心线与OM的夹角（M点为齿顶修形在齿廓的极限位置点）；ra—齿顶圆半径；αM—M点压力角；α—标准压力角；z—齿轮齿数。

啮合线单双齿啮合区的具体分布情况，如图3所示。图中：N1N2—理论啮合区；B1B2—实际啮合区；N1D和N2C—双齿啮合区；CD—单齿啮合区；B1M1和B2M2—齿顶修型在啮合线的影响区。

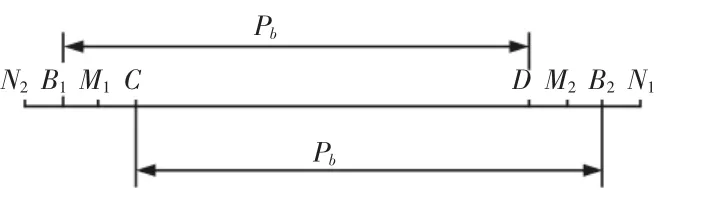
图3 啮合线上单双齿啮合区的分布Fig.3 Distribution of Single and Double Tooth Meshing Area on the Meshing line

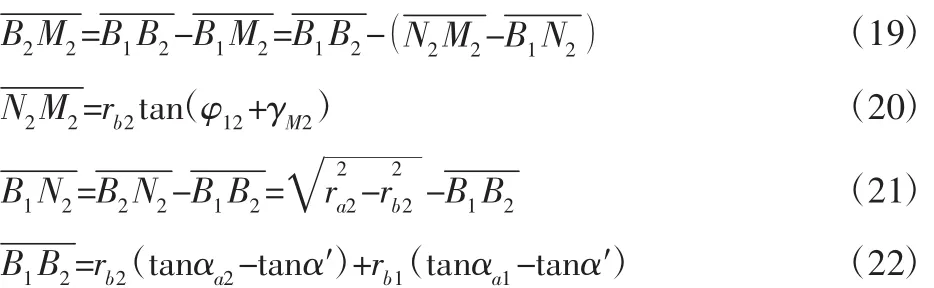
同理，可得双齿啮合区B1M1的长度。

式中：下角标 1，2—主从动轮；rb1、rb2—主从动轮基圆半径；αa1、αa2—主从动轮齿顶圆压力角；α′—啮合角。

3.3 齿向修形误差计算模型

齿轮的齿向修形采用抛物线修形方式，如图4所示。则齿向修形量cm可表示为：

式中：Cn—齿宽方向的最大鼓形量；B—齿宽；x—齿宽方向坐标。

图4 齿轮齿向修形Fig.4 The Tooth Shape Modification of the Gear

沿齿轮啮合方向的误差量在齿轮啮合过程中可近似为定值，其值可取cm的平均值表示：

4 案例分析

本例采用两个相同的齿轮啮合进行案例分析，采取的齿轮的参数如下：齿数z1=z2=46，模数m=7mm，压力角α=20°，齿宽b1=b2=21mm，弹性模量E=206GPa，泊松比ν=0.26，齿轮额定转速nz=1840r/min，齿顶修形量Ca=0.002mm，齿顶修形长度La1=La2=2mm，齿宽方向的最大鼓形量Cn1=Cn2=0.003mm。为了分析方便假设啮合齿对在恒定扭矩下运行。

利用采用的齿轮时变啮合刚度模型得到的直齿轮时变啮合刚度曲线，如图5所示。

基于齿轮变刚度传递误差模型可以得到周期性时变传递误差，理想误差模型和考虑轮齿修形的传递误差模型的对比曲线，如图6所示。图中可以看出理想传递误差是在单双齿啮合区阶跃式的周期性曲线，齿顶修形影响的是双齿啮合区的传递误差，对单齿啮合区没有影响，并且严格推导了齿顶修形在双齿啮合区的具体影响区间，针对算例模型齿顶修形长度为2mm时，双齿啮合区两侧26.8%为影响区（由于齿轮参数相同影响区对称）。齿向修形在啮合线方向对的传递误差的影响近似认为定值，因此啮合过程的误差变化是相同的。

图5 齿轮时变啮合刚度曲线Fig.5 Time Varying Meshing Stiffness of the Gear

图6 理想误差模型和考虑轮齿修形误差模型对比曲线Fig.6 Ideal Error Model and Comparison of Gear Modification Error Model

为了进一步验证提出的理论传递误差模型的准确性，与Munro等[3-4]通过试验测得的齿轮传递误差数据进行对比分析。Munro关于传递误差的试验通过测定周期性误差的啮合频率下的各级谐波的幅值与相角，并通过叠加原理得到试验条件下的齿轮传递误差曲线，相应的参数，如表1所示。为使理论与试验对比的准确性，采用试验参数进行模型建立和计算，同时通过式（10）将理论误差曲线展开成傅里叶级数的形式，基于精度要求仅展开至前3次谐波即可，理论传递误差曲线与试验曲线的对比情况，如图7所示。

理论曲线与试验曲线的最大相对误差为7.69%，理论曲线与试验曲线的吻合性良好，验证了基于时变啮合刚度为基础的齿轮传递误差模型的准确性，如图7所示。产生误差的原因主要是为了提高理论模型的通用性，理论模型考虑了齿轮的齿顶修形和齿向修形因素对齿轮传递误差的影响，而试验使用齿轮并未进行相应修形，因此理论曲线的误差范围偏大。但另一方面提高了理论模型的适用范围。

表1 试验条件下传递误差各级谐波幅值和相角参数Tab.1 The Amplitude and Phase Angle of the Transmission Error at all Levels Under the Test Condition

图7 理论传递误差曲线与试验曲线对比Fig.7 Theory Transmission Error Curve and Experimental Error Curve

5 结论

（1）建立了基于齿轮时变啮合刚度的传递误差计算模型，同时考虑了齿顶修型和齿向修形对传递误差的影响，并利用傅里叶级数展开得到了传递误差的主要谐波阶次便于与试验数据对比。

（2）分析啮合过程和原理，准确建立了齿顶修形对齿轮啮合区的影响区间模型；得到齿向修形的误差影响模型。

（3）结合具体案例得到周期性的齿轮传递误差曲线：齿顶修形长度为2mm时，双齿啮合区两侧26.8%为影响区；理论曲线与试验曲线对比，最大误差为7.69%，曲线的吻合性良好，验证了基于时变啮合刚度为基础的齿轮传递误差模型的准确性。