基于GA-BP和小波-SVM算法的风电场短期功率预测

3

(1.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043;2.天津市市政工程设计研究院，天津 300380；3.河北省分布式能源应用技术创新中心，河北 石家庄 050043)

0 引言

风力发电的功率预测和传统能源发电有着较大的不同，影响风功率的主要因素是天气预报的准确性，风速和风向的变化都可能导致风电场发电功率的变化[1]。这导致了风功率的准确预报有着一定的难度。

对于风电场功率预测，国内不少学者做了研究，李莉等[2]运用CFD流场理论对风速进行了预测，得到的风速数据与实际相比较有着较理想的效果。杨锡运等[3]基于相似数据并运用支持向量机的方法对风速进行短期预测，与实际较为贴近。周世琼等[4]运用自回归滑动平均模型对风速进行预测，较能反应实际风速情况。在功率预测上，黄俊生[5]运用支持向量机与小波变换的方法对风功率进行了有效预测，与实际风功率的误差较小。彭怀午等[6]和杨晓祥[7]分别用人工神经网络的方法对风电场发电功率进行了预测，得到了较为理想的效果。本文采用组合预测方法对风电场功率进行短期预测。

所收集的数据来自华北某风电场，具体包括历史功率数据和数值天气预报数据，数值天气预报数据包括风速、风向、温度和湿度4个因子。首先将收集到的数据经过预处理，剔除坏值点、保证完整性，然后再通过mapminmax函数进行归一化，消除因数据本身量纲等因素对输入向量所带来的影响，提高预测精度。然后将数据作为模型的输入，输入到小波-SVM网络，遗传神经网络模型之中，得到2种预测算法的预测结果。根据得到的预测结果，通过最大信息熵原理，求取各种算法的权重系数，将权重系数与对应的预测结果相乘得到最终预测结果，预测效果明显变好。

1 GA-BP网络预测模型

遗传算法是美国密歇根大学约翰.霍兰德(John Holland)教授提出的。该算法是在综合考虑了遗传与进化理论的成因之后，形成并行随机搜索最优化的方法。其将引入自然界的生存法则来作为寻优的尺度，通过对上一代种群的选择、交叉互换、变异来寻找适应度最好的个体，该个体较之前的个体具有良好的表现，可以较好地优化相应的系数。

遗传算法优化的BP神经网络主要包括3个部分，分别是初始化神经网络模型、相应系数的优化、神经网络的预测。根据输入与输出量的维度来判断输入节点数，输出节点数，并通过相应的经验来确定隐含层的节点数、将权重与阈值进行遗传算法的优化，最终得到适应度最好的个体、通过初始化后的网络和遗传算法优化后得到的个体对测试集数据进行预测并得到预测结果。

遗传算法优化的BP神经网络主要以下这5个部分进行预测得到适应度最好的个体。

(1)种群的初始化。每个个体的编码是根据输入层到隐含层之间的连接权重、阈值以及隐含层到输出层之间的权重与阈值组成的，根据网络的结构即可以唯一确定该网络。

(2)适应度函数。适应度函数(f)即通过网络上一步确定的权重与阈值进行下一步计算得出的预测值(Ok)与实际值(Yk)的绝对误差值

(1)

(3)选择。根据俄罗斯转盘赌的原理，按照误差比例的大小来绝对选择的概率

(2)

(4)交叉互换。按照个体的编码，采用蒙特卡洛方法对编码数列进行交叉互换

aij=aij(1-r)+aijr

(3)

式中,r=rand(0,1)。

(5)变异。按照生物学变异原理对编码上的数值进行一定的变异可能会使下一代种群中产生性质优良的个体，对于网络训练也可能会出现优良的权值与阈值，提高预测结果的精度。

(4)

式中,g为当前迭代次数；Gmax为最大进化代数；amax和amin分别为基因上下界[8-9]。

在运用前面算法介绍的基础之上，、对华北某风电场2017年06月01日～10日每隔15 min 取一个气象条件数值和功率数值进行发电功率的短期预测。为了提高神经网络预测的泛化能力，故将数据分成2个部分即06月01～08日作为数据的训练集，06月09日～06月10日为测试集。对网络所有数据都要进行归一化处理。训练完成之后，对数据进行反归一化处理，得到最终的预测数据，根据预测数据与实际数据比较结果，可以进行误差分析和不确定度分析。

首先将遗传神经网络初始化处理，网络的拓扑结构同BP神经网络的相同，权值可以达到60个，阈值为11个，遗传算法的个体编码长度为71个。同时设置种群规模为10，进化次数为50代，交叉互换的概率为0.3，变异的概率为0.1。将数据输入遗传神经网络，根据遗传算法的计算原理，将权重系数与阈值进行遗传变异操作， 最终得到适应度最好的一组权重系数与阈值的种群个体。将此个体带入测试集数据并与实际值做比较，训练过程与训练结果如图1、图2所示。

经过遗传神经网络的训练之后，均方根误差为3.810，决定系数为0.981，最大绝对误差为6.19，平均绝对误差为2.48，准确率为95.1%，合格率为95.8%。对单纯的BP神经网络而言，在最大绝对误差、均方根误差，决定系数与准确率上面有了较大的提升，在计算时间上比传统神经网络要快很多，且误差指标在传统神经网络的基础上稳中有升，是一种较好的、值得推广借鉴的预测方法。

图1 适应度曲线

图2 功率预测曲线

2 小波-SVM网络预测模型

2.1 小波-SVM原理

小波变换是一种对信号时间-尺度的分析方法，通过将信号在不同尺度进行细化分析，最终去除噪声信号的分析方法，有效地表现信号原始状态的一种标准形式。与经典的支持向量机原理不同，在对信号进行分解之后，通过采用合适的阈值，将信号中的噪声滤除后，输入到SVM训练模型之中，得到网络的预测输出。

小波-SVM模型主要由小波的分解，阈值的选择与滤波2个环节组成。

2.1.1 小波的分解

(5)

其重构公式为

(6)

在小波函数的选择上，本设计采用Daubechies小波，该小波没有显性表达式，但是其在时域上是有限支撑且其与整数位移正交归一，使该小波在风功率预测上面有着优异的性能。

2.1.2 阈值的选择与滤波

经过分解之后的小波信号存在着一定的噪音，应通过选择合适的阈值对噪音信号进行滤除。Donoho提出了VisuShrink方法，维数较大的情况下，该方法可以给出最优阈值，Donoho给出了证明在大量风险函数下可以获得近似理想的去噪效果。

(7)

式中,σn为噪声信号的标准差；N为信号长度[10-12]。

2.2 小波-SVM预测

将风速，风向，温度，湿度数据，运用Db8小波分解成3个低频分量和3个高频分量后，采取通用阈值法并设计相应滤波器去噪。后分别经过小波处理过的每个高频或低频分量输入到SVM训练模型中进行计算，通过网格搜索使c、g2个参数分别在-10到10之间步长为0.5搜索概略的c、g值后，再以步长为0.05精确搜索c、g值，最终得到最优的c、g值。如图3、图4是经过网格搜索得到c=1.802 5，g=0.341 51的最优c、g值以及等误差带为0.005的误差等高线图。

图3 SVR参数选择等高线图

图4 SVR参数选择3D图

将得到最优的c、g值输入到SVM训练模型之中，得到网络最后的预测值如图5和图6所示。

图5 训练集功率预测曲线

图6 测试集功率预测曲线

小波-SVM测试集的均方根误差为15.569，决定系数为0.967，最大绝对误差为6.45，平均绝对误差为2.59，准确率为94.8%，合格率为95.6%。通过预测结果发现经过小波变换后的数据比较圆滑，几乎没有毛刺和噪声信号，这是比支持向量机的预测效果好的地方。然而风速是一个具有较大随机性的量，小波变换滤波过后可能把短时间内的大风速量去除掉，这也是其误差系数都较SVM模型较低的原因之一。虽然小波-SVM在训练效果上逊色于SVM模型，但若是在网络输入出现一定的偏差，气象预报数据出现偏差时，小波-SVM可以将网络的噪声通过阈值信号去除，更好地还原风速以及天气情况下有着较好的适用情况。将上述2种方法的预测结果列于表1。

表1 GA-BP网络和小波-SVM预测结果

由预测结果分析得2种预测方法各有优点，小波-SVM算法的去噪效果更好，遗传神经网络的拟合效果更佳，所以决定系数更高。如果把2种方法进行组合各取其优点，那么预测效果一定会更好。本文采用最大信息熵原理的方法将2种算法组合，进行风电场短期功率预测。

3 基于最大信息熵原理组合预测模型

3.1 最大信息熵原理

最大信息熵原理是E.T.Jahnas提出的在对于只掌握未知分布数据的一部分特性时，而对这些分布最不确定、最随机的一种推断就是对数据的一种最准确的推断的思路衍变而来。对于离散序列，信息熵

(8)

式中，pi为每种预测方法的权重；n为预测方法的种类。所谓最大信息熵原理，就是要解出式(8)的一个最大值。根据E.T.Jahnas的理论证明，必须选择一种无偏估计才能满足信息熵的最大。所以式(8)有2个约束条件

(9)

式中,σi为等式的二阶中心距[13-15]在满足上述2个等式的条件下，求解出H(p)的最大值，p所对应的值即为每种预测方法的权重系数，将每种权重系数与对应的单一预测方法的值相乘再相加后即可得最终运用最大信息熵原理的组合预测数值。

组合预测结果如表2。

表2 组合预测结果

图7 功率预测曲线

组合预测结果的均方根误差为5.224，决定系数为0.993，最大绝对误差为4.42，平均绝对误差为2.33，准确率为95.9%，合格率为96.4%，将2种预测方法的优点进行组合预测，得到了更好的预测效果，可以作为最终预测结果来指导生产生活实践，为风电场的短期规划作出相应的调整。

根据上述算法计算出的预测值加载到新的工作区之中，根据目标函数与约束条件确定函数，运用Matlab内置的求解非线性函数来求解函数的最大值点。

运用上述函数计算得到组合预测的权重，根据权重系数得到最终的预测值如图7所示。

3.2 不确定度分析

对于每一时刻的风功率的确定数值，在实际情况中是有一些偏差存在导致有一些差别，所以对风功率系统做不确定度分析可以更好地指导风电场的发电功率。根据已经得到组合预测的风功率数值，将每一点的预测值与真实值做差值得到每一时刻的误差。画出上述误差值的概率密度曲线，运用假设检验的方法确定误差的分布规律，根据分布规律确定误差情况，确定不确定度。根据组合预测得到的预测值与实际功率的差值得到的误差值做概率密度函数，得到概率密度，对此概率密度曲线拟合得到表达式，求出上5%分位数和下5%分位数的数值，即可确定在显着性水平为10%的情况下，预测的不确定度水平。如图8是误差概率密度函数以及拟合出的曲线，图9为分布函数曲线，对分布函数曲线积分可知下5%分位数值为-3.19，上5%分位数为3.84，在10%的显着性水平之下，预测风电场发电功率的不确定度为[-3.19,3.84]。

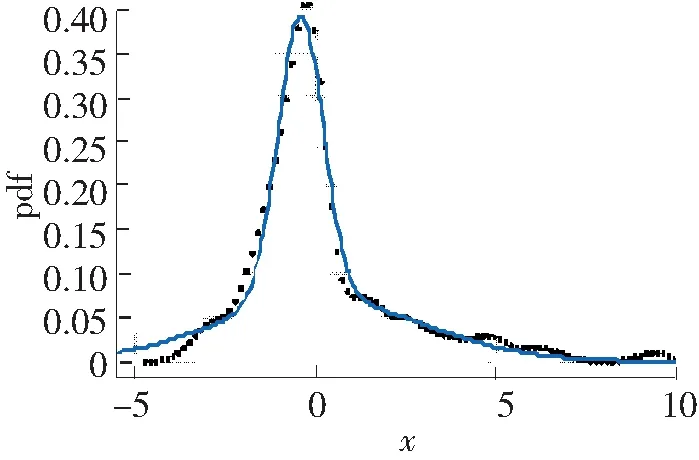
图8 误差概率密度曲线

图9 误差分布函数曲线

4 结束语

风电场功率预测是近些年学者们的研究热门话题。本文采用的是遗传算法优化的BP神经网络和小波-SVM模型对华北某风电场进行短期功率预测，该算法的仿真结果证明组合预测的精度要高于对应的2种单一预测模型的预测精度；该算法的实现需要历史数据的支持，所以不适用新建风电场的功率预测；该算法利用了数值天气预报数据的信息，所以整体预测效果和各点的预测效果都较好。该方法整体较简单，预测精度高，效率快，对计算机性能要求低，适用广泛。