一种谐振软切换方案的能量分析研究

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

0 引言

近年来，随着软开关技术的蓬勃发展，电力电子设备逐渐实现小型化，高频化[1]。为了使软开关技术达到新高度，国内外学者对其进行深入研究。其中，有关谐振软切换技术的研究是人们特别关注的问题之一，相继展开一系列研究并取得一定的进展。目前研究者对这类问题的研究大多采用传统的电路分析方法，如文献[2]和文献[3]中提及的谐振软开关电路工作模式，它的局限在于缺乏对电路整体性的分析，而且对电路中能量的转换过程没有涉及。针对这一情况，本文建立相关的数学模型，采用能量补充的方法，通过导通各开关管为电感和电容进行充电，从而维持振荡，可使开关管周期性地过零，实现开关管的软切换。根据电路结构介绍了环流的产生以及抑制环流的主要方法，以使电路的设计能最大化的实现软切换。采用的新型研究方法拓宽了对谐振软切换技术提供的研究手段，提高了这一技术的研究水平，为后续研究者提供一种新思路。

1 谐振型软开关逆变电路

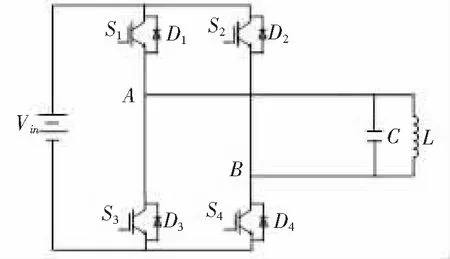
图1 并联谐振型逆变电路

谐振软开关逆变电路根据电感电容不同组合方式可分为串联谐振电路和并联谐振电路， 本文拓扑结构采用并联接法，如图 1 所示。

逆变电路结构由直流电压源，S1～S44个功率开关管(选用IGBT)构成全桥逆变网络，D1～D44个快恢复二极管，并联电感电容组成，该接法限流能力强，而且短路保护可靠性高。当电路正常工作时，需要设计开关顺序使开关管互补导通，驱动电路负责产生2组相反的驱动信号。S1和S4为一组，S2和S3为另一组。电路中，当S1和S4导通时，S2和S3截止，2组不能同时导通，要留有一定的死区时间。

直流电源加在2组互补导通的开关管上，将直流电逆变成为方波交流电，AB两端产生的正负交替的交流电经过并联LC谐振网络输出平滑的正弦波形。电感和电容中的能量在交换过程中会出现零点，此时切换开关将会实现ZVS。

2 能量补充模型

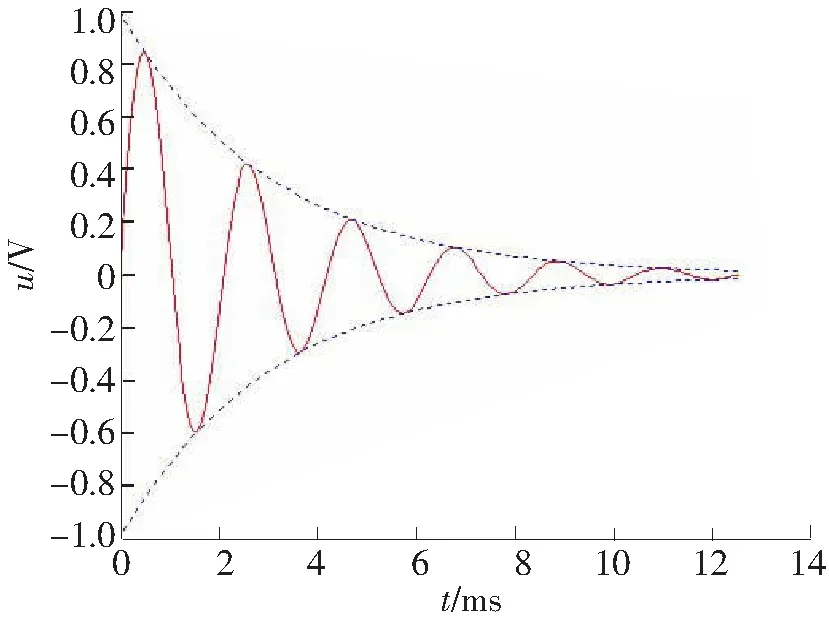
图2 电压随振荡衰减波形

考虑到实际电路中电阻的存在且品质因数Q值为一有限值，使得逆变桥两端电压vAB振荡为一衰减过程，并且最终稳定在零值。也就是说，此时vAB不能产生周期性的过零点，不能为软切换及时提供条件[4]。如图2所示，实线曲线反映谐振时电压u随时间t变化关系。

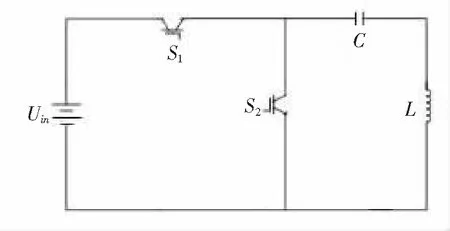
图3 能量补充电路模型

实际电路中，电阻是主要的耗能元件，将电源的有功功率(电能)转化为热能形式消耗掉[5]。而电感和电容是储能元件，电容中存储着电场能，电感中存储着磁场能，当电路受到激励时会产生振荡，并且逐渐衰减。这时电磁能与电场能相互转化，彼此交换能量，即电路总能量守恒。在谐振状态下稳定地存储在电路中的能量WS=0.5CU2，这个能量是在电路接通后由外电路提供的，此后会在短时间内产生振荡而消耗。只要外电路不断地提供有功功率，这个振荡过程就可以保持近似等幅变化。而在谐振状态下不再需要外部提供电能，因此，为了使电路能够工作在谐振状态下，人们提出能量补充电路。图3给出一种能量补充电路的拓扑结构。

由上面的分析可知一个网络在有剩余能量的时候，它会在其自然频率点上做自由振荡，而且幅值会逐渐减小，直至为零。图4、图5给出含有负载损耗时电路中电感和电容能量转化过程衰减变化曲线。如图4为三维变化曲线，图5为相轨迹曲线。

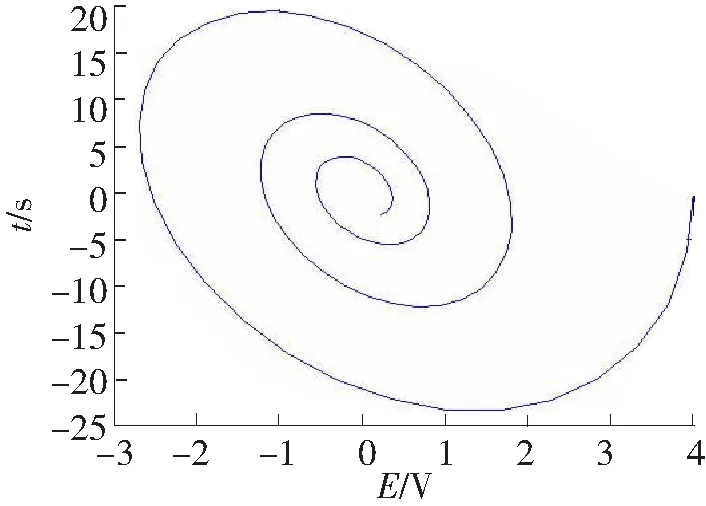
图4 能量变化三维图

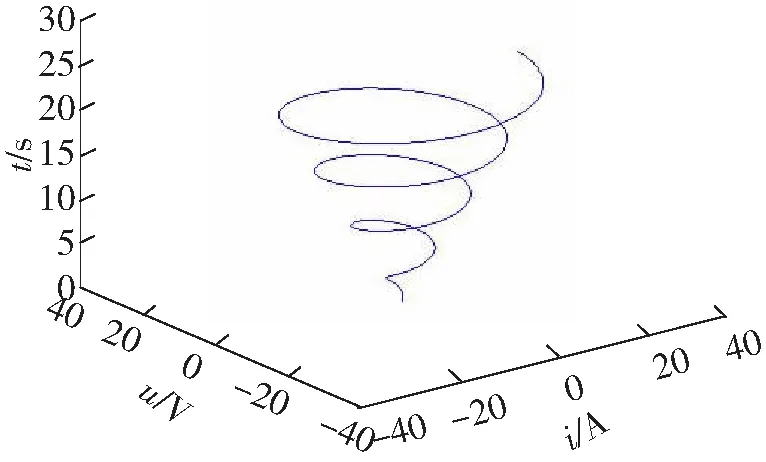
图5 能量变化相轨迹曲线

图3给出了一种能量补充电路的拓扑结构图。该电路工作模态为：

模态1：S2导通，S1关断；模态2：S1导通，S2关断。

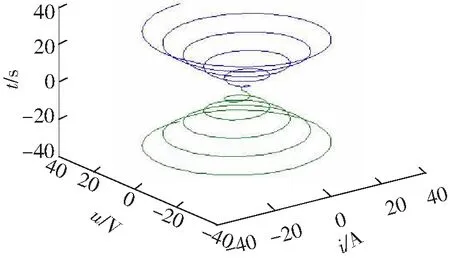
图6 能量补充电路

当运行在模态1时，电容C，电感L，开关管S2构成一回路，由于储能原件L、C的存在使电路在初始能量下做减幅振荡，振荡频率由L和C共同决定，直到能量消耗完毕。当运行在模态2时，电容C，电感L，开关管S1，电源Uin构成一回路(电流方向规定为电源正级流出为正方向)。此时，直流源的接入为谐振网络注入能量，从而弥补状态1中损失的能量。理论上完成一周期的能量补充。该设计如图6所示。图中上方表示初始能量衰减振荡过程，下方表示能量补充过程。

3 电路模型与能量分析

在模型建立之前假设：电容C为理想元件，不存在寄生成分；开关管均为理想器件，开合是瞬间完成的。本文仅研究正方向运行情况，该并联谐振电路等效电路模型如图7所示。图中r为谐振回路的等效电阻，C与L分别表示谐振电容和谐振电感，由基尔霍夫定律列写电路的KVL及KCL方程如下

图7 并联谐振电路等效电路模型

(1)

(2)

求得电容两端电压Vp的表达式

(3)

式中,id(0)为初始电流值。在其他条件不变的情况下，可得Vp的表达式

(4)

此时，初始相角θ为

(5)

计算出

(6)

带入式(3)，得出

(7)

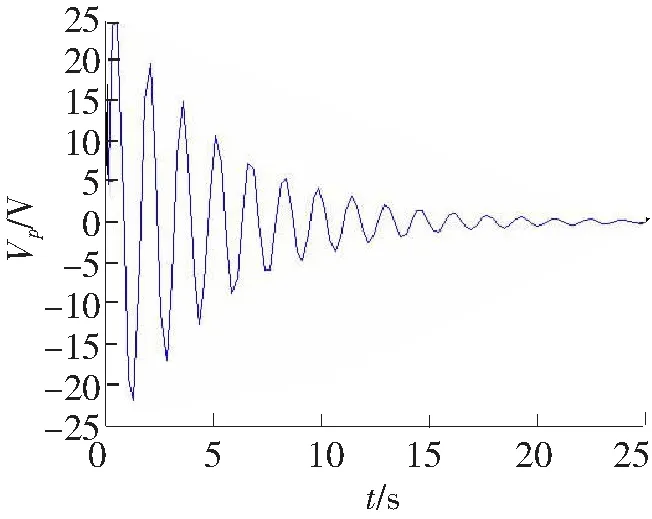
图8 电容电压振荡电压

由上述分析可知电路在理想情况下，谐振网络的等效阻抗r1为零。T为时间常数，电路在初始状态下相角θ=0，式(7)可表示为

(8)

用Matlab仿真软件绘制Vp随时间t变化曲线如图8所示。从仿真图可知电路在进行能量交换过程中，电容两端电压呈减幅振荡状态，且存在过零点。

4 能量补充环节

由上述分析可知能量在振荡的过程中不断衰减直至为零。如图9所示。曲线中纵轴表示能量，电压，电流变化，横轴表示时间变化。

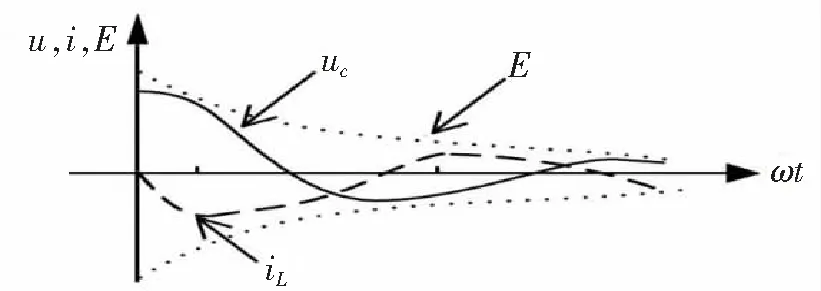
图9 能量，电压，电流变化曲线

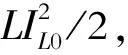
当LC谐振网络处于无损状态时，只要电感预充电电流最大临界值IL0等于此时刻流过负载的电流值I0，那么电容两端的电压就与无负载时相同，电容两端电压便会做正负交替的等幅振荡，理论上实现能量无损运动。所以，在实际设计中应满足IL0>I0,就可补充内阻损失掉的能量，且实现谐振软切换。

5 谐振型逆变器环流问题

5.1 环流的产生及危害

由上述分析可知，合理控制开关管通断可以为谐振槽注入能量，实现能量平衡以维持振荡。但在实际中，通过参考大量文献可知，使用该方法得到的谐振电容两端电压波形并非平滑的正弦波形，在过零点有明显的突变，这是因为在开关过程中有电流尖峰产生，即没有实现真正的零电压关断，在逆变回路中产生了环流。环流的存在对系统产生极大的影响，若环流过大，不但会使换流失败，而且会损坏开关管，使逆变“颠覆”。因此在设计电路时要先对环流进行分析。

环流的产生是由于硬切换引起的，目前导致非零切换的主要因素是频率的变化和开关管关断延时。关于频率的变化在文献[6]中有详细介绍，这里只分析开关管延时影响。导致开关管关断延时第一个原因是控制电路对谐振槽路采集信号时，由于驱动隔离的加入使得信号拾取时产生延时，时间为0.3～0.5 μs，二是开关管关断时产生的拖尾电流出现延时，为0.2～2.5 μs。本电路中，开关管关断如果不在谐振零点时会将电容短路掉，此时开关管中会有很大的电流流过，开关管会产生很大的di/dt，这将使开关管应力增大，从而影响电路的稳定运行。

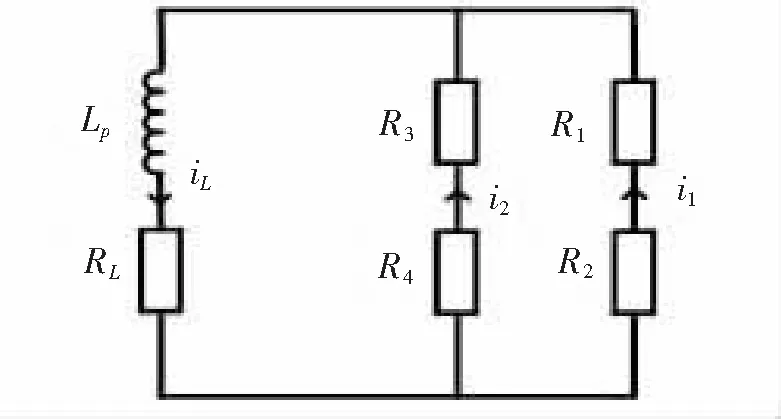
图10 等效电路图

5.2 环流仿真模型

当电路中存在环流时，电源和电容被短路，环流会在电感，续流二极管，等效电阻以及开关管中流动[7]。这里假设T1和T4延后关断，那么VD2和VD3会导通续流，图1等效电路如图10所示。图中，RL为电感内阻，R1为开关管T1内阻，R2为二极管VD2内阻，R3为二极管VD3内阻，R4为开关管T4内阻，T1和VD2的电流为i2，T4和VD3的电流为i2，电感电流为iL。由等效电路可知

(9)

列回路KVL方程

(10)

可得

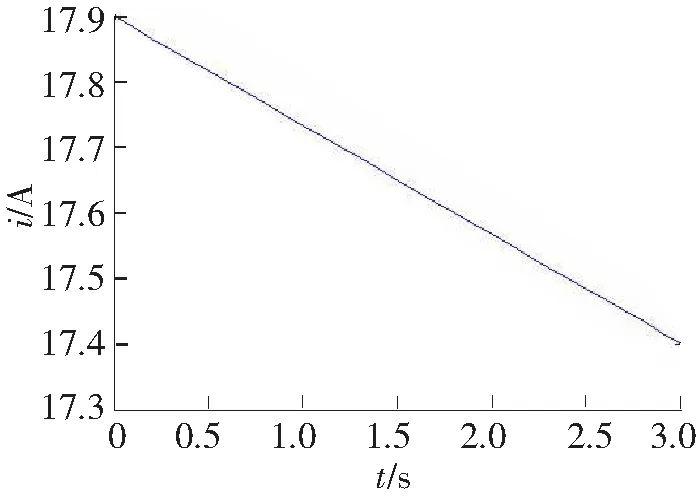
图11 开关管电流变化曲线

iL=i0e-(RL+Req)/Lpt

(11)

那么

i1=kiL

(12)

其中

(13)

对此环流模型进行Matlab仿真，仿真参数选取：R1=R2=R3=R4=0.001 Ω,RL=0.25 Ω,iL=30.8 μH,i0=36.2 A，可计算出等效电阻Req=0.001 Ω。仿真得开关管电流如图11所示。

由曲线可知，当电路中产生环流时，开关管中的电流约为17.9 A，而正常工作的电流约为2 A，即开关管中的电流将变化为正常工作时的8～9倍，对开关管产生极大的损害。所以，人们提出相关方法来抑制环流。

5.3 环流抑制方法

目前，环流抑制主要应用在电机的调速装置中，另外，也有学者研究不间断电源UPS中环流的产生和抑制，并取得一定成果。结合国内外学者的研究成果，总结出环流抑制的2种主要方法。一种是依靠主电路的结构去抑制，该方法是通过硬件设计去阻断环流通路，使之与主电路断开，可有效地解决回路环流问题。但该方法也有一定的弊端，使得电路硬件成本增加，且出现电流断续情况。另一种是通过软件编程去抑制环流的产生，该方法采用先进的控制策略，通过控制主电路主动抑制环流，是一种经济可靠的方法，本文采用该方法抑制环流的危害。可以通过控制信号相位补偿对驱动信号进行调节，即通过提前一角度θ开通开关管可对延时信号进行补偿，从而保证谐振回零时切换开关管，实现软开关,且环流危害降为最小。其中θ可由下式确定

θ=2πftd

(14)

θ的大小由开关频率和关断延时时间确定。

因此，只要检测出二极管续流时间就可求得环流时间。目前，信号处理器DSP功能强大，具有可靠的频率捕获能力，采用DSP可以方便且精确地求得环流持续时间[8]。在频率f和关断时间td都已知的情况下，带入公式(14)便可求得延时角，从而抑制环流。

6 结论

采用能量的观点分析了谐振变换电路的软切换过程，运用能量补充的方法对储能原件进行充电以维持振荡，使电路实现软开关，损耗降为最小。此外，还介绍了环流的危害和抑制措施，并搭建仿真模型对环流进行仿真。本文的分析思路基本可以克服传统方法对谐振电路分析的缺陷，在不改变拓扑结构的前提下，实现开关管的软化，极大地拓宽了对谐振软切换技术的研究手段。