汽车顶盖喷涂轨迹的优化

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

在经济迅速发展和消费者对汽车品质需求日益提高的整体环境下，市场对汽车的喷涂质量也日益重视。随着我国综合国力的提升和技术水平的提高，汽车喷涂水平迅速提高，汽车行业的各类先进工艺技术得到了广泛应用，喷涂质量也在不断改善。然而，由于汽车喷涂工艺过程的复杂性和特殊性，汽车喷涂质量始终是值得研究的课题。为了提升喷涂质量，降低喷涂过程中人为因素引起的喷涂误差，手工作业逐渐被机器喷涂所替代[1]。

自法国的SAMES公司研发出世界上第一套粉末静电喷涂设备后，静电喷涂技术由于其在喷涂效率、表面均匀度等方面表现突出，获得工业界的普遍认可。瑞士ABB 公司、日本三菱公司、德国杜尔公司等自动化设备生产商[2]，纷纷将专业的工业控制技术应用到喷涂设备。李发忠[3]利用点云逆向CAD重构技术将复杂表面模型简单化，为生成喷涂轨迹提供了依据。黎润伟[4]将复杂曲面进行三角划分，继而构建STL点集数据，实现喷涂轨迹规划。喷涂机器人轨迹规划正向着智能化方向发展。为实现对复杂工件的表面喷涂轨迹规划问题，本文利用Matlab编程，计算出涂料经过高速旋杯式静电雾化器[5]形成涂层时，涂层轨迹间的最优重叠距离，通过对喷涂轨迹[6]重叠距离的计算和对喷涂轨迹的优化，提高了喷涂质量和喷涂效率。

1 相邻轨迹间涂层重叠距离计算

汽车表面进行喷涂时，由于每次喷涂的直径有限，因此需要进行多次往复循环喷涂才能完成整体平面的喷涂工艺过程。在汽车喷涂过程中，涂料经过高速旋杯式静电雾化器到达汽车顶盖时，在离心作用和静电作用下[7]，涂料分子在各个方向上的运动速率不同，因此在喷涂表面涂层的厚度分布是不均匀的。在循环喷涂时，为了最大程度上实现整体涂层厚度的均匀性，需要将相邻喷涂轨迹进行重叠化。通过确定雾化器中心轨迹之间的距离，即可确定涂层重叠轨迹。

直角坐标系中表示的涂层厚度叠加俯视图，如图1所示，O为雾化器中心点在工件表面的垂直投影，雾化器运动方向与x轴平行，v为雾化器移动速度方向，R为涂料经雾化器在工件表面所形成喷涂轨迹的半径值，d为2次喷涂轨迹之间的重叠距离。根据β分布模型[8]，得到喷涂轨迹剖视图，如图2，f(r)为涂层厚度，涂层1表示雾化器沿x轴正方向运动时得到的涂层模型，涂层2表示雾化器与第一次喷涂轨迹重叠距离为d时沿x轴负方向运动时得到的涂层模型，涂层1与涂层2相交部分形成重叠轨迹，涂层厚度为涂层1厚度与涂层2厚度的叠加。

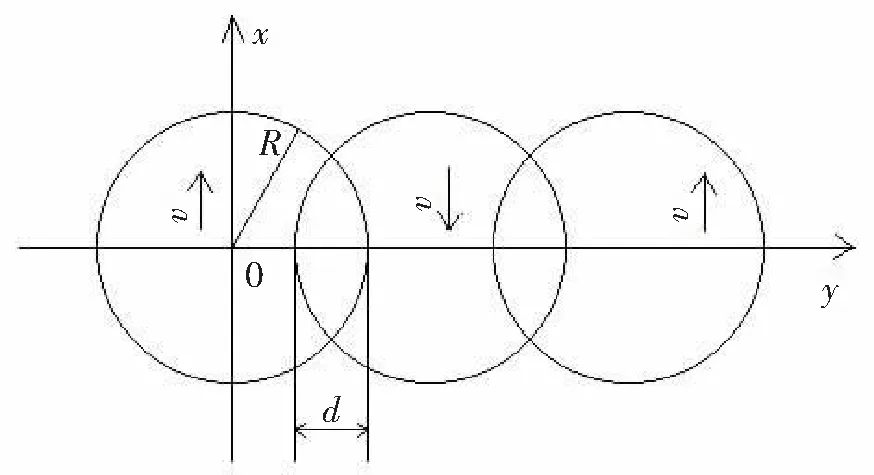
图1 涂层厚度叠加俯视图

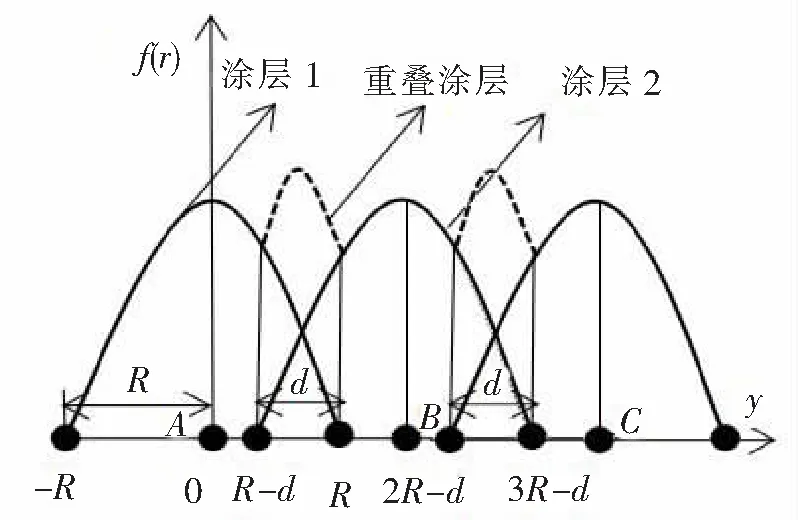
图2 喷涂轨迹剖视图

由于往复喷涂过程中，相邻喷涂轨迹之间的重叠距离均与涂层1和涂层2的叠加规律相同，因此只需对涂层1和涂层2中心点之间的涂层厚度进行研究即可[8]。当喷涂过程中往复运动速度均匀时，对涂层叠加后才能使涂层的均匀度达到更高，因此将喷涂过程中雾化器的移动速度设置为定常数。

若在喷涂过程中，雾化器与车身表面一直保持垂直状态，车身工件上任一点s处的坐标值为(x,y,z)，式(1)表示点s处的涂层厚度

(1)

式中，f1(x,y,z)为s点位于第一条喷涂轨迹时得到的涂层沉积厚度；f2(x,y,z)为s点位于第二条喷涂轨迹时得到的涂层沉积厚度；f3(x,y,z)为s点在第一条喷涂轨迹与第二条喷涂轨迹的重叠部分时得到的涂层沉积厚度。

根据文献[9]测厚仪测量实验平板上不同位置的涂层累积速率数据，式(2)表示y与F的关系

F=f(y)=k(R2-y2)

(2)

式中，k为喷涂厚度调整系数，可以根据实验数据进行调整；R为雾化器喷涂到工件表面的半径值；y为s点与雾化器中心点之间的距离，其值与t相关。

3条喷涂轨迹涂层沉积厚度平面方程

(3)

2 汽车表面喷涂轨迹优化模型的建立和求解

实际喷涂过程中，静电雾化器固定，涂料在静电力和离心力的双重作用下，呈现环形的分布状态。经过逆向工程重构CAD模型和点云模型切片算法[3]对圆环截面曲线进行离散化，得到离散点二维分布图。为方便计算，将离散点二维分布图优化为二次函数进行建模。

2.1 设计变量

喷涂质量由喷涂轨迹与涂层厚度决定。喷涂轨迹与喷涂路径、喷涂方向相关，涂层厚度与喷涂半径、喷涂轨迹间的重叠距离、雾化器移动速率相关。当涂料体积一定时，喷涂半径与涂层厚度成反比；喷涂轨迹间的重叠距离与涂层厚度成正比，喷枪移动速率与涂层厚度成反比。为了获得最优涂层厚度，需选择合适的喷涂半径、喷涂轨迹间的重叠距离和雾化器移动速率。

影响涂层厚度的因素是喷涂半径R、喷涂轨迹间的重叠距离d、雾化器移动速率v，当喷涂半径R和雾化器移动速率v确定后，只需优化喷涂轨迹间的重叠距离d，因此优化变量可确定为

X={d}

(4)

2.2 目标函数

保证涂层厚度合理的情况下，要求涂层厚度尽可能均匀，若以实际喷涂涂层厚度与理想喷涂涂层厚度的差值为目标函数，则存在正负差值相互抵消的情况，因此，在满足实际情况需要且尽量减少计算复杂性的基础上，取实际喷涂涂层最大厚度与最小厚度的差值进行优化，其中qmax(d)表示最大涂层厚度，qmin(d)表示最小涂层厚度，待优化的目标函数为

(5)

2.3 约束条件

从实际角度出发，当喷涂轨迹间的重叠距离大于R，为了达到更高的涂层厚度可以通过调整喷涂半径R和喷枪移动速率v，因此喷涂轨迹间的重叠距离在完全不重叠与重叠半径为喷涂半径R之间。喷涂轨迹间的重叠距离需满足以下条件

0≤d≤R

(6)

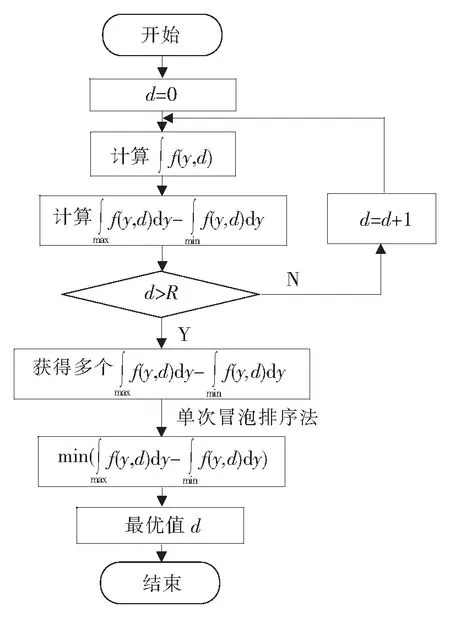
图3 喷涂轨迹重叠距离的优化流程图

2.4 计算最优重叠距离

采用单次冒泡法计算相邻轨迹间的最优重叠距离，涂层厚度与s点到雾化器中心点的距离y、重叠距离d相关，喷涂轨迹重叠距离的优化流程如图3所示。

假设雾化器与车体表面的距离为250 mm，雾化器喷涂形成的锥形涂层在车体表面形成的涂层半径R=40 cm，根据β型涂层沉积速率[7]得

(7)

在对喷涂轨迹之间的重叠距离进行优化时，先将喷涂重叠距离d的初始值设置为0，计算出各点处的涂层厚度和该喷涂重叠距离d下最大涂层厚度与最小涂层厚度差值，若喷涂重叠距离d的值不大于雾化器喷涂形成的涂层半径R，则将喷涂重叠距离d的值增加一个单位值(增加的单位值越小，计算出的最大最小涂层厚度差值越精确，选择的最优喷涂距离d的值越接近实际值)，为了便于分析，选取1作为每次重叠距离d的递增值，并继续计算该喷涂重叠距离d下的各点的涂层厚度和最大涂层厚度与最小涂层厚度差值，依次对d的值进行递增和循环计算，直至喷涂重叠距离d的值大于雾化器喷涂形成的涂层半径R，此时，基于冒泡排序法的原理，采用单次冒泡排序法对以上各喷涂重叠距离下得到的最大涂层厚度与最小涂层厚度差进行比较，将各相邻涂层厚度差值进行比较，较小者存放在后者位置，第一轮比较完毕，则最小值存放在末位置。末位置的涂层厚度差为最小涂层厚度差，该情况下得到的涂层即为最优涂层，且此时的喷涂重叠距离d为最优喷涂重叠距离。

2.5 重叠距离结果分析

根据对喷涂轨迹重叠距离的优化计算，得出当涂层半径为40.0 cm时，相邻轨迹间的重叠距离最优解为24.0 cm，此时涂层最大厚度与最小厚度的差值最小，涂层均匀度最高，汽车表面喷涂质量最好。

3 喷涂轨迹优化

3.1 汽车顶盖进行三角平面剖分

汽车喷涂表面主要由发动机盖总成、翼子板、车门总成、顶盖总成、行李舱隔板总成、行李箱盖总成、侧围总成、后围板总成组成。选取汽车顶盖总成部分为研究对象，进行喷涂轨迹规划。

在Pro_E中建立汽车车体CAD模型，由于车体顶盖曲面不规则，计算过程较为复杂，为了简化计算，在满足喷涂精度要求的情况下，参考典型的Delaunay算法思想[10]，对汽车顶盖进行网格节点初始化划分，在汽车顶盖曲面曲率变化较大的区域划分的节点较为密集，曲面曲率变化较小的区域划分的节点较为稀疏，经过计算和节点划分，车体顶盖曲面模型共划分得到40个曲面节点，汽车顶盖曲面节点CAD模型如图4所示。

将CAD曲面模型和划分得到的曲面节点以igs格式进行保存，并将曲面和点的保存文件导入逆向工程Imageware[11]软件，在Imageware中查看工件体积信息如图5，可获得工件在x、y、z轴的边界值。

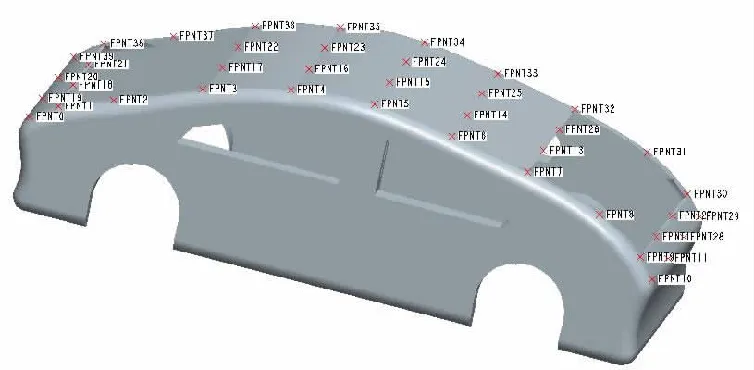
图4 汽车顶盖曲面节点CAD模型

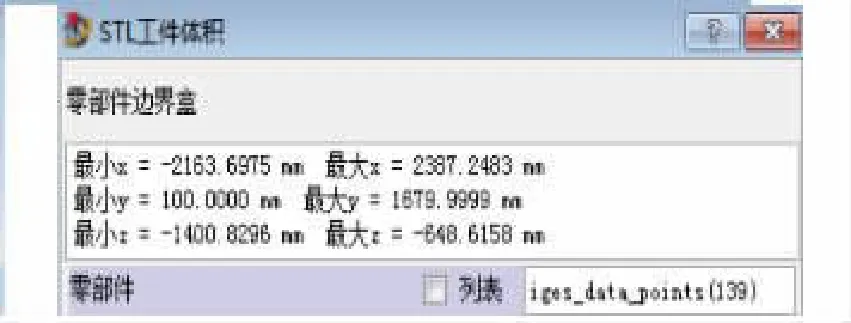
图5 汽车顶盖体积信息

如图6以汽车行业4视图的视图布局格式显示汽车模型信息和曲面的具体信息，4视图分别表示上视图、侧视图、前视图和轴测图，便于查看各曲面节点位置，获取各曲面节点的三维坐标值。

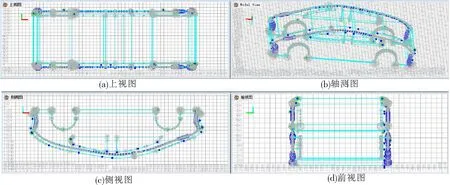
图6 汽车行业4视图显示汽车CAD模型

运用Matlab编程将曲面节点自动生成三角化离散多面体。利用三角网格模型代替曲面造型，简化求解计算出所需的曲面模型数据信息。为了便于分析和计算，将获取的曲面三维坐标值导入Matlab程序，通过三维坐标值绘制相互连接的三角面元，等效为车体顶盖曲面。Matlab实现三角剖分程序如下：

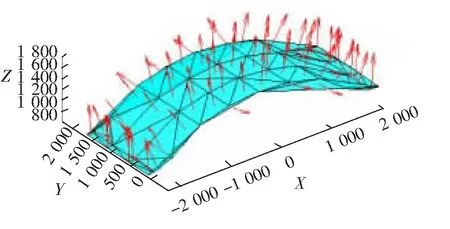
图7 车体顶盖曲面三角剖分模型

A=[-2 173.306 2, 103.958 2, 650.240 6,…];

x=A(:,1);y=A(:,2);z=A(:,3);%选取x,y,z矩阵

tri = delaunay(x,y); %三角网格划分

tr = TriRep(tri,[x,y,z]);

P = incenters(tr); %求每个三角面元的内接圆圆心

fn = faceNormals(tr); %求每个三角面元的法向量

trisurf(tri,x,y,z,'FaceColor', 'cyan', 'faceAlpha', 0.8); %画出曲面

axis equal;hold on;

quiver3(P(:,1),P(:,2),P(:,3),fn(:,1),fn(:,2),fn(:,3),1,'color','r');%画出法向量

车体顶盖曲面三角剖分模型如图7所示。

3.2 喷涂轨迹生成

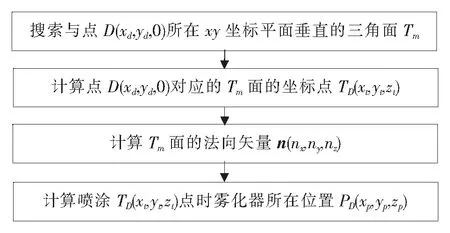
图8 雾化器位置坐标求解流程图

在三维坐标系中将车体顶盖曲面在xy平面进行投影，并对汽车顶盖投影进行网格划分。雾化器在汽车表面形成的涂层半径为40.0 cm时，相邻轨迹间的重叠距离最优解为24.0 cm，可确定相邻雾化器中心点喷涂距离为2R-d=56.0 cm。喷涂时间包括喷涂轨迹时间和转折点时间，为了尽量减少喷涂时间，提高喷涂效率，根据分片原理[9]，通过计算最小高度，减少喷涂轨迹的转折点。因此确x轴为喷涂主方向，y轴为喷涂转折方向。 根据以上规则，以车体顶盖在xy平面投影的中心点为对称中心，网格间距为56.0 cm进行网格划分，得到多个网格交叉节点。

根据xy平面的网格交叉节点求解汽车顶盖的三角剖分模型对应的坐标值。三角剖分模型对应的x、y坐标值与网格交叉节点的x、y坐标值一一对应，三角剖分模型z坐标值需根据所在离散三角平面进行计算，计算步骤如图8所示。

已知三角面的3点TD1(x1,y1,z1)、TD2(x2,y2,z2)、TD3(x3,y3,z3)确定三角面法向向量

(8)

由三角面的点TD1、法向量n，根据点法式确定三角面平面方程

nx(xi-x1)+ny(yj-y1)+nz(zk-z1)=0

(9)

三角平面上对应TD点的坐标

(10)

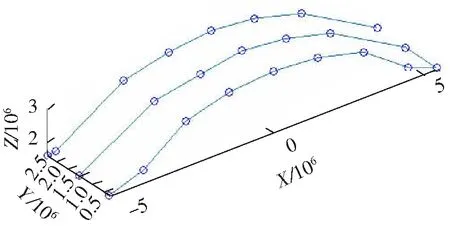
图9 汽车顶盖喷涂轨迹图

雾化器所在位置PD点的坐标

(11)

式中，h为雾化器与汽车表面的距离。

根据以上推导过程，绘制出车体顶盖喷涂轨迹图，如图9。

4 结论

(1)选取β分布函数，对涂层沉积厚度模型进行研究，计算出相邻轨迹间的最优重叠距离，最大程度上实现了汽车喷涂过程中涂层厚度的均匀性。

(2)以汽车顶盖为例，获取复杂曲面的喷涂轨迹，并完成对喷涂轨迹的规划，为进一步实现对复杂曲面的喷涂轨迹优化提供了理论基础和实践指导。