自适应滑模摩擦补偿在隔膜张力控制中的应用
王 韬,王恒升,周 君
(1.中南大学 机电工程学院,长沙410083;2.深圳市佳得设备有限公司,深圳518110)
隔膜是锂电池的关键内层组件之一。 隔膜分切机是将大卷径、宽幅的隔膜卷分切成小卷径、窄幅的隔膜卷的设备,隔膜张力是决定产品质量最关键的因素。 在此以隔膜放卷张力控制为背景,在放卷过程中,隔膜卷的卷径及惯量随时间变化,加之摩擦、轴辊布局等其它不确定因素的影响,使得放卷系统成为一种集多输入、多输出、非线性、强干扰等为一体的复杂机电系统。 针对隔膜分切机在放卷过程中,由于负载惯量的时变性与摩擦的不确定性导致张力波动大的问题,提出了自适应滑模摩擦补偿控制算法。
1 放卷轴动力学模型和摩擦模型
1.1 隔膜分切机放卷系统
隔膜分切机放卷系统的结构如图1 所示。 在放卷过程中,非线性极强且时变的摩擦力矩总是存在的。 根据放卷辊的动力学模型和工程经验有:为保证放卷张力稳定,需对放卷轴的摩擦进行实时补偿。
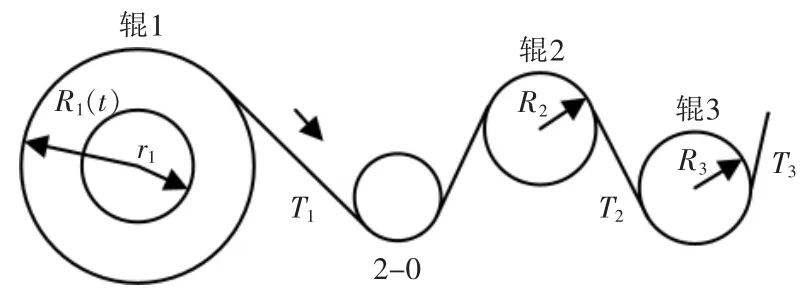
图1 隔膜分切机放卷系统Fig.1 Unwinding system of diaphragm slitter
为了减少摩擦对伺服运动系统的影响,学者们提出了多种控制和补偿方案,基于摩擦力矩模型的前馈控制方案是最直接的方法之一。 文献[1-2]对摩擦产生的机理进行了分析研究,提出了几种摩擦建模方法,并对模型的实际应用进行了分析。 摩擦模型有静态的和动态的,动态模型中最常用的是GMS模型和LuGre 模型。 文献[3]对GMS 模型的机理和应用进行了详细的描述。 针对摩擦模型的参数在系统运行时会动态变化,文献[4-5]采用基于LuGre 模型的自适应控制对摩擦力矩进行前馈控制,满足伺服运动系统的速度和位移跟踪精度。
对于负载惯量时变和摩擦不确定的问题,在此提出基于LuGre 模型的自适应滑模ASM 控制补偿算法。时变参数的自适应律由Lyapunov 函数推导得到, 为了防止时变参数出现过大甚至为负的现象,在此引入了自适应映射算法。
1.2 放卷轴动力学模型
在图1 中, 辊1 为伺服电机驱动的放卷辊,采用力矩控制模式;r1为套于辊1 的锂电池隔膜卷内径;R1为隔膜卷外径;辊2 为张力传感器辊,用于测量放卷隔膜张力; 辊3 为电机驱动的主速度辊,采用速度控制模式,产生隔膜传送基准速度。 由牛顿第二运动定律,放卷轴放卷时的动力学方程为
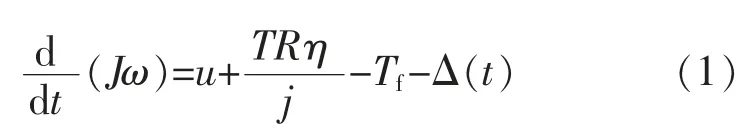
式中:J 为放卷轴的总转动惯量;ω 为放卷电机角速度;η 为传动机构传动效率;j 为传动比;u 为电机力矩;T 为放卷张力;R 为隔膜卷外径;Tf为放卷机构中的摩擦力矩;Δ(t)为包括外界干扰和模型不确定部分的总的不确定性,且设不确定性Δ 有界,可表示为
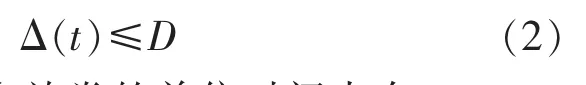
由文献[7]可知,在放卷的单位时间内有
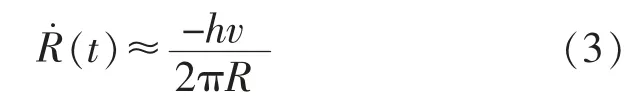
式中:h 为隔膜厚度;v 为放卷轴的线速度。
联立式(1)(3),得
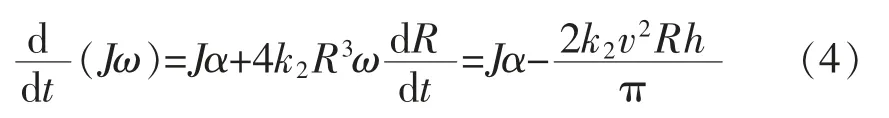
由于h 为μm 级,为便于计算,可略去式(4)最终结果的第2 项,简化后放卷轴在放卷时的动力学方程为
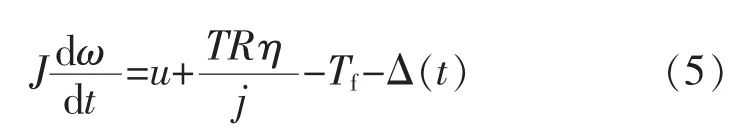
而放卷轴单独转动(即空载)时的动力学方程为

比较式(5)(6)可知,放卷轴放卷与空载的区别是有、无隔膜张力力矩的影响。 在此拟通过放卷辊的速度跟踪试验来验证摩擦补偿算法的有效性,并将该算法应用于隔膜放卷张力控制中,以提高张力控制精度。
1.3 摩擦模型及特性分析
对于式(6)中的Tf,采用广泛使用的动态模型——LuGre 模型,其表达式为
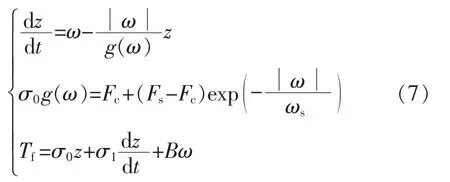
式中:z 为2 个接触面之间鬃毛的物理偏移量;ω 为角速度;σ0,σ1,B 分别为鬃毛刚性系数、阻尼系数和黏滞摩擦系数;Fc为库伦摩擦矩;Fs为静摩擦矩,且Fs>Fc;ωs为斯特里贝克速度。 根据ω 和ωs的大小,将摩擦分为2 种状态——黏附状态 (当|ω|<ωs)和滑动状态(当|ω|>ωs)。
由摩擦特性可知,当ω 较大,即纯滑动摩擦状态时,dz/dt≈0;当ω 较小且换向时,即在黏附状态时,dz/dt 存在较大值。 因此对于纯滑动摩擦状态,依据式(7),有
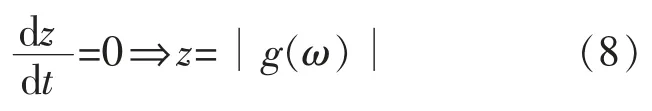
根据式(7)(8),滑动状态时,基于LuGre 模型的摩擦力矩为
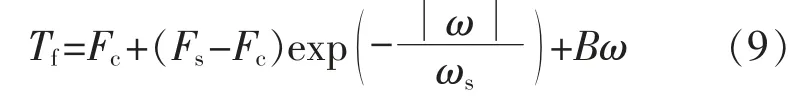
通常ωs都非常小,根据指数函数的性质,当ω较大时,式(9)右边的第2 项近似为零。 因此,滑动状态时LuGre 模型可近似为

2 自适应滑模摩擦补偿方案
2.1 补偿控制器的设计
根据张力的产生原理,放卷张力控制的本质即对放卷轴进行目标速度跟踪控制。 为此定义角度误差eθ和转速误差eω分别为

定义跟踪误差的线性滑模面为

式中:θd为给定角位置;θ 为实际角位置;ωd为给定
角速度;ω 为实际角速度;c>0。
实际工程中,可以将S 控制在一定范围δ 内。在此引入一个新的滑模面SΔ,定义为

其中
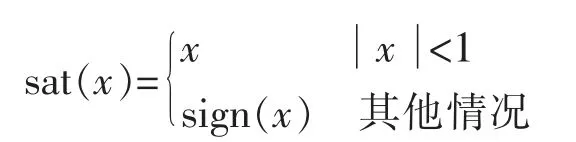
式中:sat(x)为饱和函数。 SΔ具有以下性质:
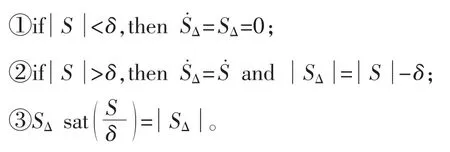
由SΔ的结构和定义可知δ 的大小直接决定了控制器的精度。
由式(6),得到放卷电机的驱动力矩为

因式中的J 和Tf不确定,由式(15)计算出的驱动力矩不能达到设计的速度要求。 为此,基于滑模控制策略所设计的控制律为
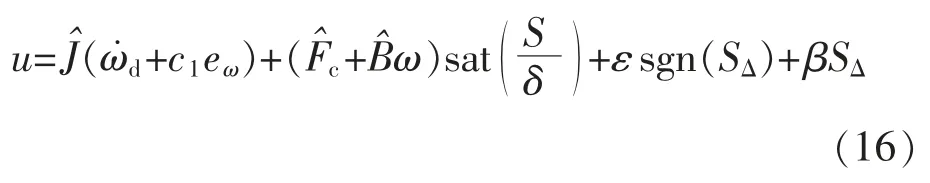
在理想情况下,当SΔ=0,此时由式(16)估计的惯量和摩擦力矩就应该是其真实值。 由式(16)得到控制系统的结构如图2 所示。
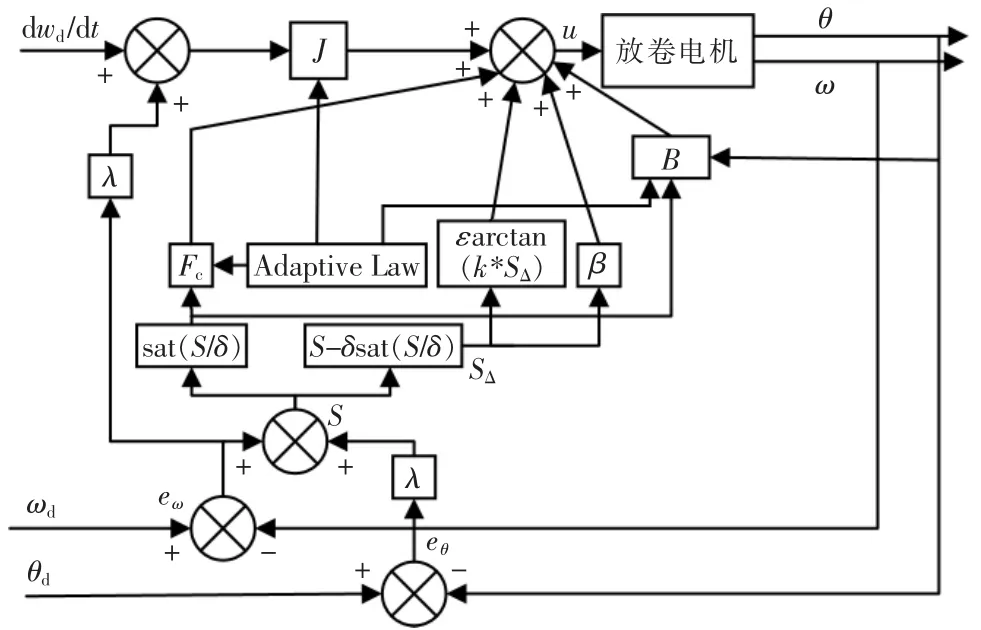
图2 自适应滑模摩擦补偿控制系统框图Fig.2 Block diagram of ASM friction compensation control system
2.2 系统稳定性分析
将控制律(16)和式(10)代入式(6),有
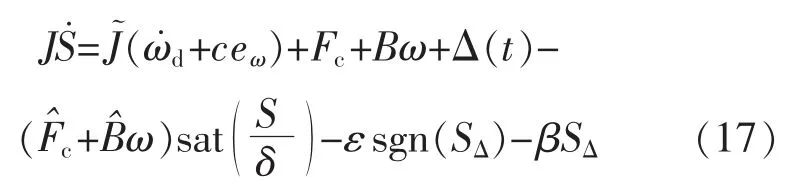
其中
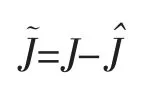
令
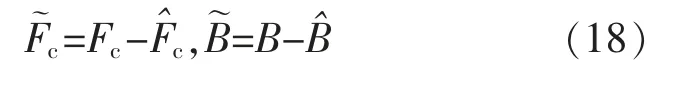
定义的Lyapunov 函数为
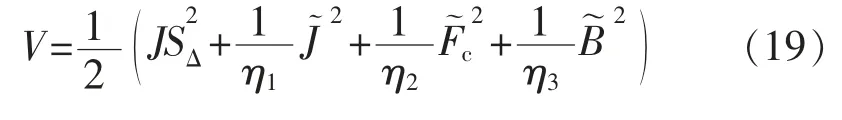
其中

式中:η1,η,η3为正增益。对式(19)求导,将式(17)代入,可得:
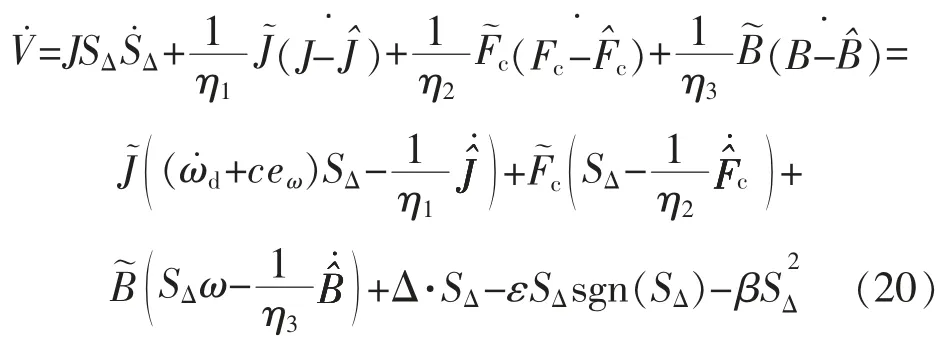
由式(20),可得J,Fc,B 的自适应律为
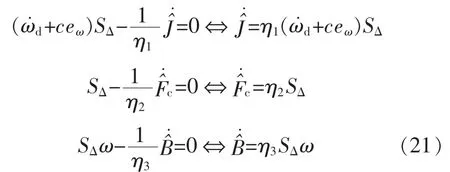
将自适应律(21)代入式(20),有

式中:ε,β 均为正常数,且ε>D。 综合符号函数的性质为
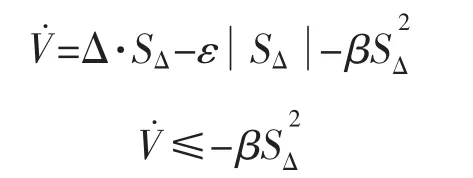
故


其中投影映射算法,Projξ(·)定义如下:
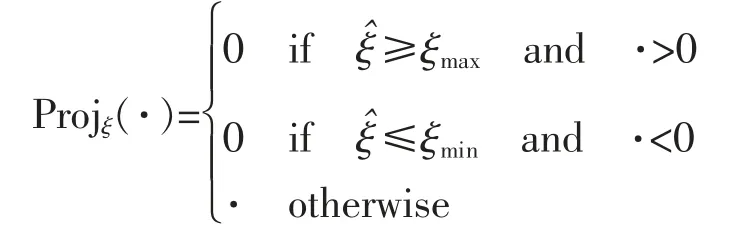
至此设计完成ASM 摩擦补偿控制器。
3 仿真
3.1 仿真设置
为验证所提出ASM 控制器能够正确估计出模型参数,并能够实现速度跟踪,在此进行了仿真。
单轴驱动的仿真采用式(6)给出的模型。 其中,伺服电机的力矩环假定为理想,即其传递函数为1;无扰动影响,仿真步长为0.0001 s;模型参数为J=0.0156,Fc=0.32,B=0.025,均取国际单位制。
转速给定设置为变加速曲线,即10+2sin(t),单位为rad/s;给定位置和给定加速度可以通过对给定速度进行积分和微分运算得到。
ASM 控制器的参数通过仿真调试,设定为c=5,β=10,ε=0.12,δ=0.01,η1=5,η2=20,η3=10。
需要在线估计的参数初值均设置为0。
3.2 仿真结果
仿真结果如图3 和图4 所示。 由图可见,转动惯量约在0.005 s 就收敛于真值,摩擦矩约在0.6 s达到其真值,系统很快正确地辨识出模型参数。
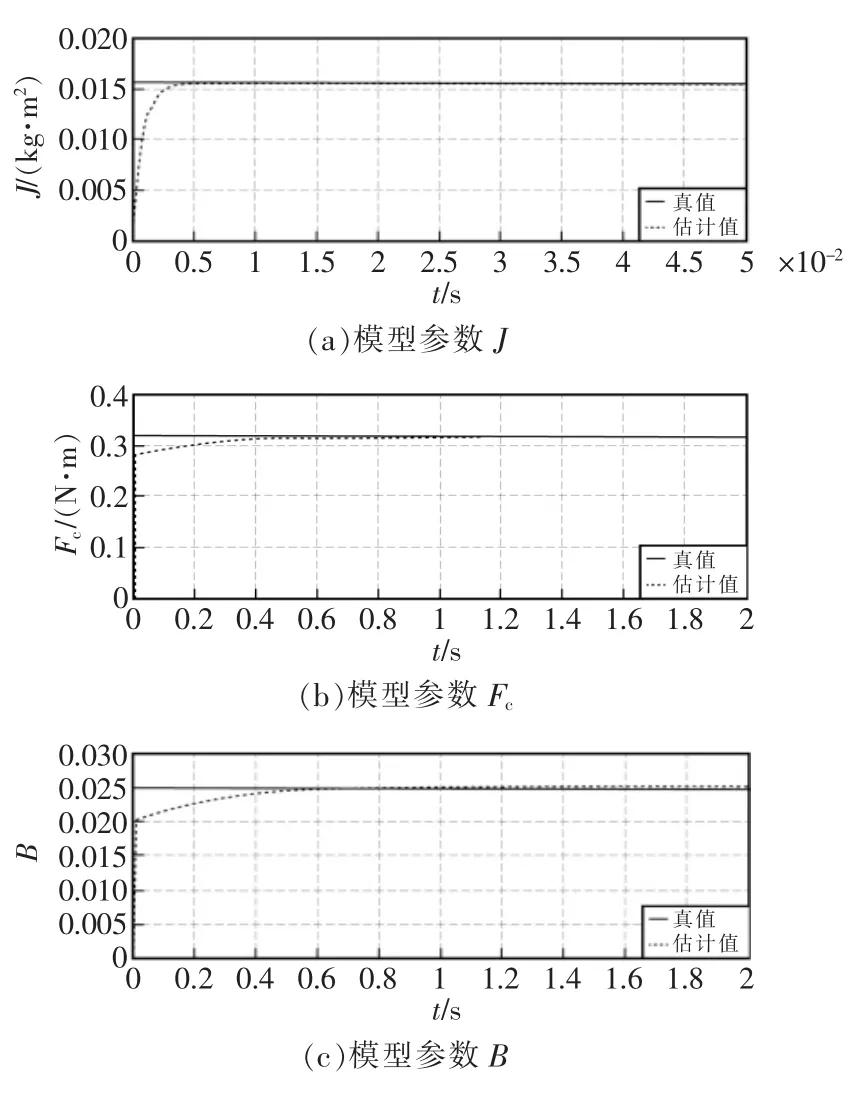
图3 模型参数估计曲线Fig.3 Model parameter estimation curve
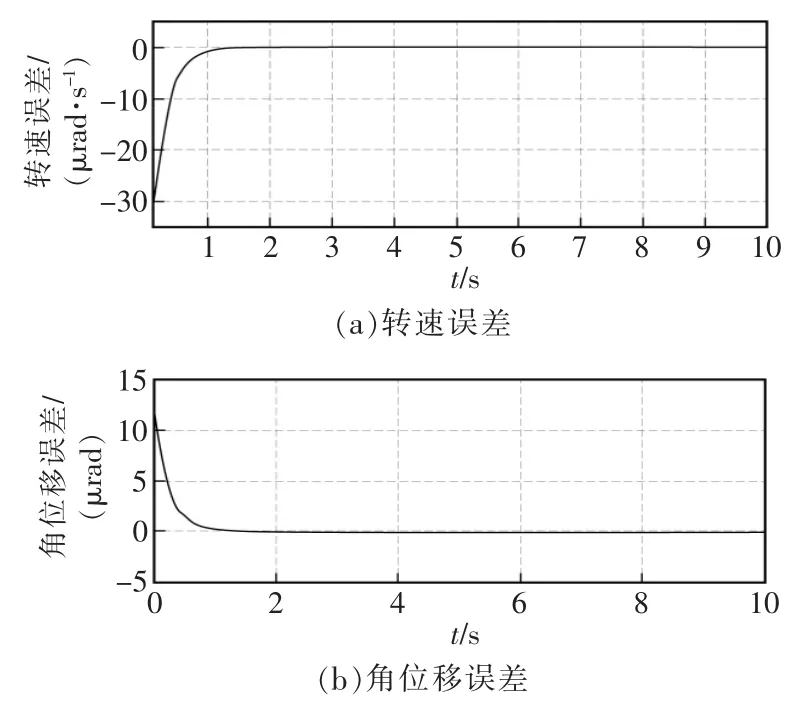
图4 ASM 控制跟踪误差Fig.4 Tracking error of ASM control
图4 为控制系统的转速、角位移的误差曲线,在模型参数估计值收敛后(约0.6 s),误差曲线趋近于0。
4 试验验证
试验分切机包括放卷轴和主驱动轴,采用被动式的表面收卷方式。试验分切机实物如图5 所示。2个驱动轴分别由倍福的伺服电机AM-8042 和AM8052 驱动, 控制器采用倍福的CX-3E80AE 型PLC。 程序扫描周期为1 ms。

图5 试验分切机实物Fig.5 Experimental slitting machine
4.1 速度跟踪试验
在ASM 控制器的速度跟踪试验中,对放卷电机用力矩控制模式。 设置
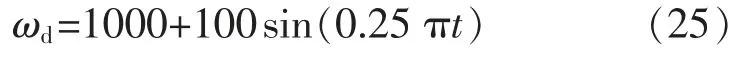
式中:ωd为目标转速,(°)/s。
ASM控制器的参数选取为c=20,β=0.15,ε=0.05,δ=3,η1=3×10-8,η2=2×10-5,η3=1.5×10-6。
为了降低系统的不确定性,放卷机构的转动惯量使用放卷恒速试验计算出的真实值为0.0125 kg·m2;为了加快系统的收敛,使用曲线拟合的方法识别出摩擦参数的初值,并将其估计值限定在给定区间内,其中Fc初值为0.2605 NM∈[0.2581,0.2635],B 的初值为0.006842∈[0.006593,0.007091]。 该试验原理在此不再赘述。
试验结果分析如下:
设置的目标转速与实际转速如图6 所示,发现ASM 控制能满足对目标转速跟踪的要求。 其中,超调量约为25%;调节时间约为4 s。这表明ASM 控制器的动态响应快速、平稳。
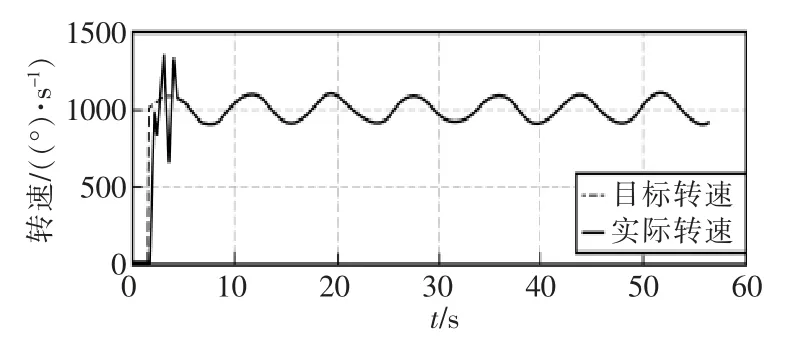
图6 ASM 控制和PD 控制下的速度跟踪情况Fig.6 Angular velocity tracking under ASM control and PD control
ASM 控制的角位移误差、 速度误差曲线如图7,8 所示。 由图7 可见,速度误差的均值为0,速度误差的稳态误差为±0.3 rad/s,其中系统的固定误差为±0.2 rad/s。 由图8 可见,ASM 控制的角位移稳态误差为±0.015 rad。 这表明ASM 控制器的稳态误差小、精度高。

图7 仿真转速误差Fig.7 Velocity error of simulation
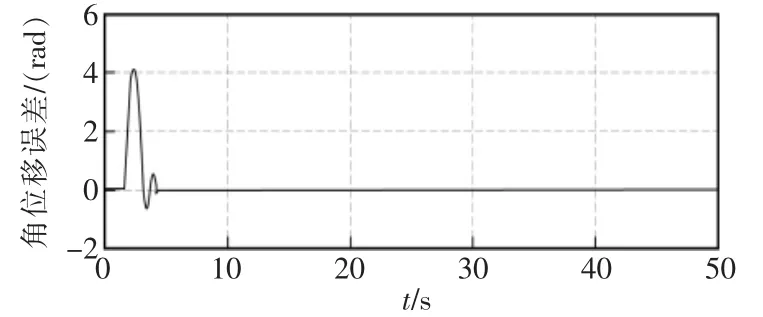
图8 仿真角位移误差Fig.8 Position error of simulation
在使用ASM 控制下的速度跟踪试验中,通过自适应律识别出的时变摩擦参数Fc和B 的变化曲线如图9 所示。
速度跟踪试验验证了所提出的ASM 控制器的控制性能和精度均能满足控制目标,同时也验证了该算法能快速识别变化的摩擦力矩,并进行有效地补偿。
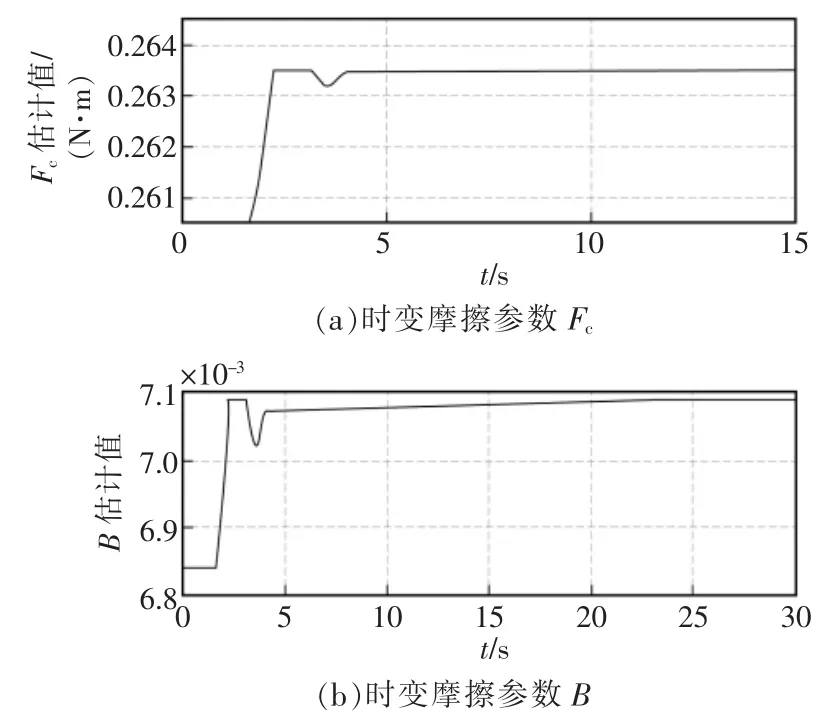
图9 摩擦参数估计值Fig.9 Estimations of friction parameters
4.2 张力控制试验
在隔膜放卷试验中,对PID+ASM 摩擦补偿和PID+静态摩擦补偿,这2 种摩擦补偿策略在分切机变速和匀速情况下放卷张力的控制效果进行了比较。隔膜放卷张力控制如图10 所示。试验所用参数见表1。
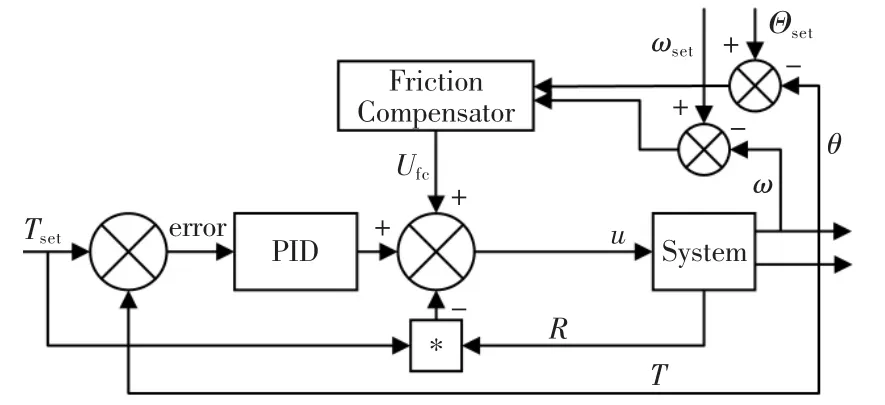
图10 PID+摩擦补偿张力控制系统框图Fig.10 Block diagram of PID+ASM tension control system
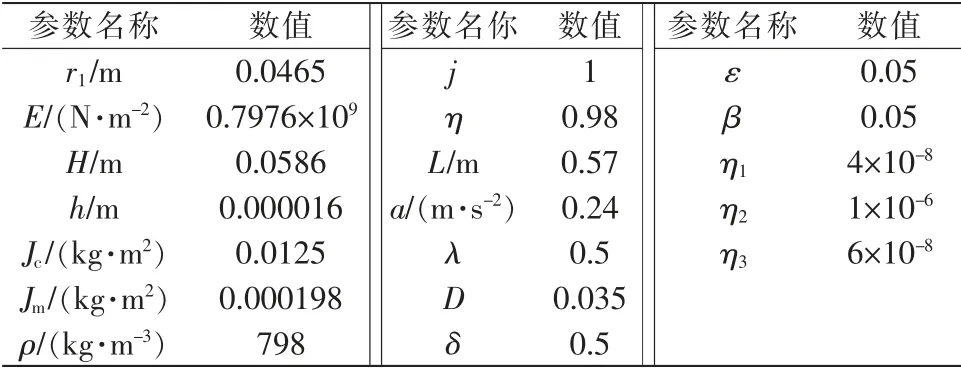
表1 张力控制试验用参数Tab.1 Parameters for tension control test
PID 控制器参数为KP=0.12,KI=0.1,KD=0.05。
在该试验中,分别测试了2 种摩擦补偿方案在相同期望张力Tset=4 N, 变速情况下放卷隔膜张力的控制效果,试验结果如图11,12 所示。
通过对试验结果进行分析可知,在分切机变速和匀速的整个运动过程中,采用ASM 摩擦补偿的张力控制效果都更为理想,其跟踪误差更小,约为±0.7 N,而采用静态摩擦补偿的跟踪误差约为±1.5 N; 而且前者在变速过程中的控制性能也更好,加减速过程中其张力波动很小,而后者的张力波动却很明显。

图11 PID+ASM 摩擦补偿的张力控制效果Fig.11 Tension under PID+ASM friction compensation

图12 PID+静态摩擦补偿的张力控制效果Fig.12 Tension under PID+Stati friction compensation
综合上述跟踪对比试验和放卷张力控制试验可知,所设计的ASM 摩擦补偿方案能有效地对变化的摩擦进行补偿,能明显提高隔膜张力控制精度。
5 结语
针对放卷机构中存在变化的摩擦力矩进而造成隔膜张力波动的现象,根据放卷轴的动力学模型和LuGre 摩擦模型,围绕摩擦力矩补偿问题提出了ASM 摩擦补偿方案。 采用Lyapunov 稳定性理论推导得出摩擦参数的自适应律,并进行了稳定性证明。为了防止时变参数过大或为负,根据实际情况对时变参数进行映射自适应算法修正。 仿真和试验都表明,所设计的ASM 摩擦补偿方案能实现摩擦力矩的有效补偿, 并且能显著地提高隔膜分切机的张力控制精度和稳定性。

