新型控制器在加热炉温度控制中的应用研究

辛海燕，陆清茹，2，王迷迷，黄 卉

（1.东南大学 成贤学院，南京210088；2.东南大学 毫米波国家重点实验室，南京210096）

加热炉是铸造、热处理中应用得最多的加热设备，也是最主要的能源消耗设备。 加热炉用来对材料进行分段加热和冷却等，其温度参数对材料的制备和生产有很大影响，温度控制精度和稳定度直接影响着锻件的性能和能源利用的效率。 有效地提高加热炉温度控制精度以及能源利用效率，增强企业竞争力，是铸造企业所面临的重要课题。

传统PID 控制器具有结构简单、 鲁棒性强、控制精度高等优点，故国内大多将PID 用于加热炉温度控制，但由于加热炉具有非线性、较大纯滞后和时间常数的特性，难以建立精确的数学模型，以致PID 控制在加热炉温度控制中的效果并不理想。Smith 预估控制器是传统的用于时滞系统分析的控制方法之一，但它预估控制器也依赖选取精确匹配的数学模型，这在实际生产过程中很难实现，而且当存在外部扰动时，模型不能很好地与被控对象匹配，不能消除闭环特征方程中的时滞项，响应系统的稳定性。 考虑到现有方法的缺点，在此对用于加热炉温度控制的新型控制器进行了研究。 该控制器结构简单，控制规律简便，只需要在一些预先指定的控制律中调整控制参数，就可以保证闭环性能和系统稳定性。

1 加热炉数学模型

根据文献、 实际测量数据和控制经验可知，加热炉传递函数为

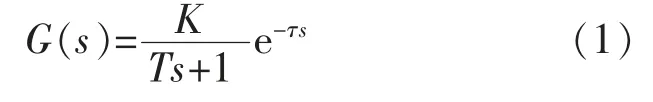
式中：K 为加热炉放大系数；T 为加热炉惯性时间常数；τ 为加热炉纯滞后时间。

在一定的可控硅导通角下，测定一组加热炉温度与时间的对应关系[1]。加热炉温度采样数据见表1。

表1 加热炉温度采样数据Tab.1 Temperature sampling data of heating furnace

将加热炉温度采样数据在MatLab 中进行曲线拟合[2-4]，可得加热炉的传递函数为

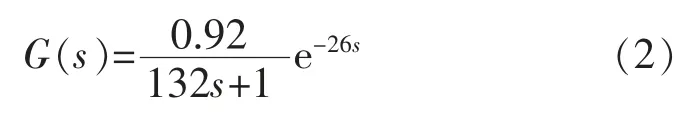
2 控制系统结构设计

在此所设计的典型控制系统结构如图1 所示。图中，Xr（s）为系统输入量；Xc（s）为系统输出量；G（s）为被控对象模型；Gf（s）为反馈通道控制器；D（s）为前馈通道控制器；Xd1（s）为系统输入扰动；Xd2（s）为系统输出扰动。 则，系统在输入量Xr（s）作用下的闭环传递函数为

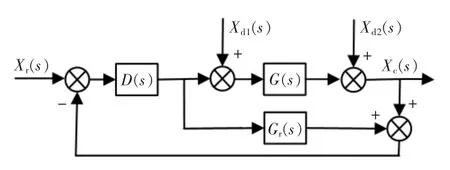
图1 控制系统结构Fig.1 Control system structure

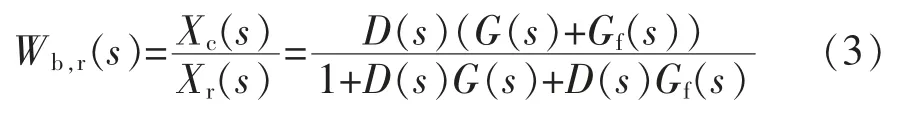
系统在输入扰动Xd1（s） 作用下的闭环传递函数为

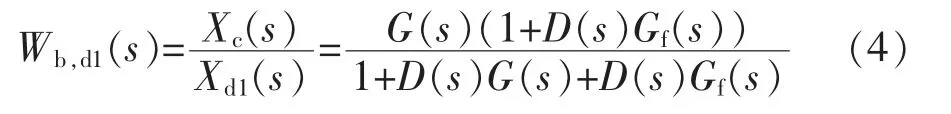
系统在输出扰动Xd2（s）作用下的闭环传递函数为

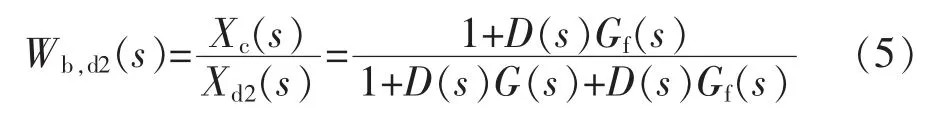
3 新型控制器设计

针对一阶纯滞后加热炉炉温控制系统， 在图1所示的系统结构中，前向通道控制器D（s）和反馈通道控制器Gf（s）可以分别设计为

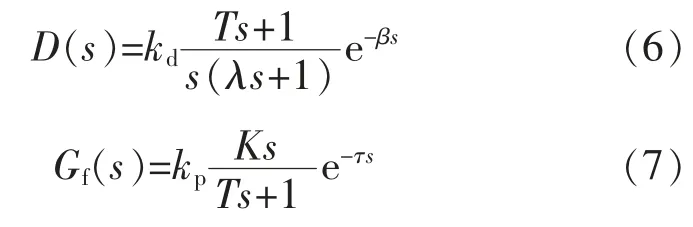
式中：β 为可调参数，当β<1，根据e 指数函数的泰勒级数展开式

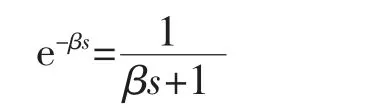
则前向通道控制器D（s）为[5]

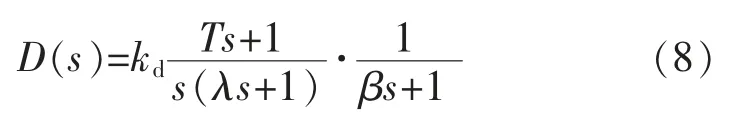
引理：考虑如图1 所示的系统结构，有

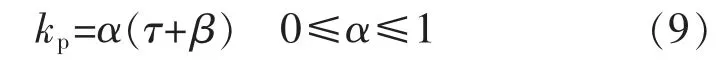
使

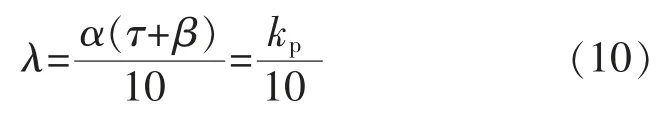
为保证闭环系统的稳定性，增益kd可以设为

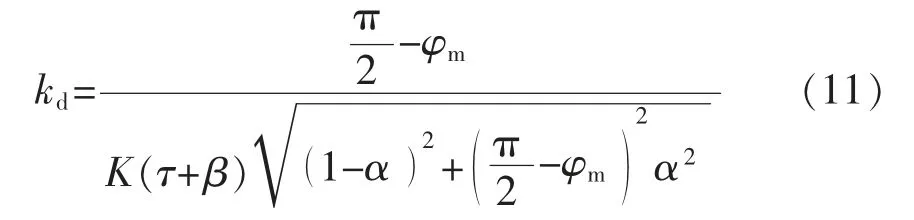
式中：φm为系统的相位裕度，且0≤α<1。 可以证明，当选择α=0.4，φm=64°时，闭环稳定性和鲁棒性均可满足。

这样，增益kd可简化为

此时，当给系统外加阶跃输入时，系统的响应如下：

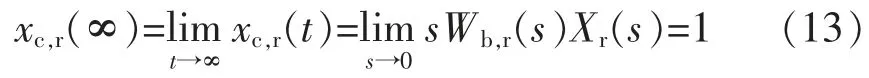
在阶跃输入扰动作用下的响应为

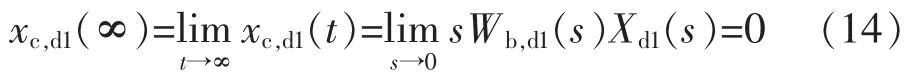
在阶跃输出扰动作用下的响应为

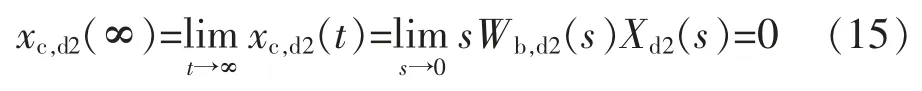
这表明，按照式（6）～式（12）所设计的控制器可以使系统具有良好的阶跃跟踪和抗阶跃扰动作用。

4 仿真结果

根据加热炉的数学模型

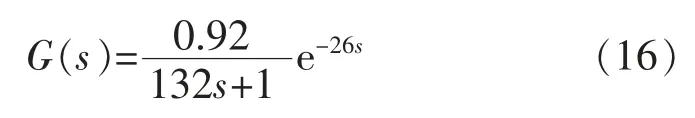
则有

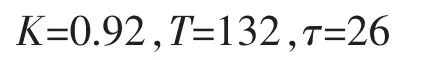
选取可调参数

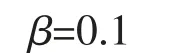
则有

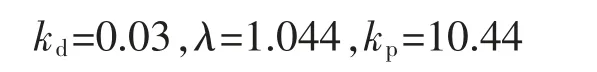
根据式（7）（8），前馈通道控制器D（s）和反馈通道控制器Gf（s）分别为

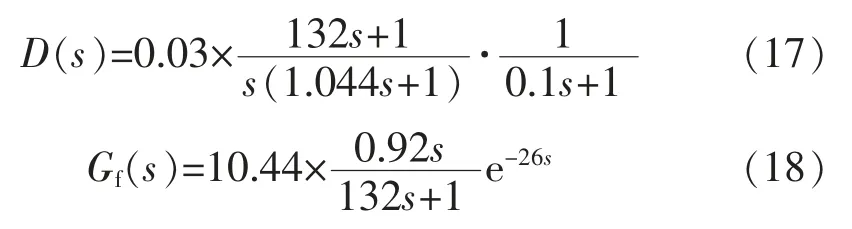
假定给定的加热炉温度为300 ℃，分别采用传统的Smith 控制方法和本文控制方法进行控制，仿真结果如图2 所示。

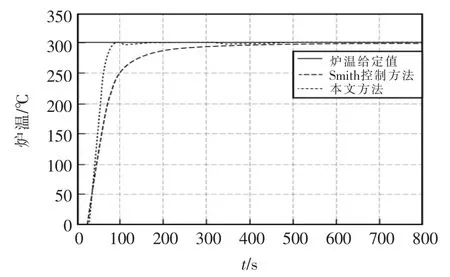
图2 本文方法和传统Smith 控制方法仿真结果Fig.2 Simulation results of this method and traditional Smith control method

由图可见，Smith 控制方法响应时间较长，本文方法具有良好的炉温阶跃跟踪特性。

在图2 时间响应的基础上，分别在系统响应时间为250 s 和400 s 时，加入阶跃扰动，系统响应结果如图3 所示。 由图可见，在阶跃扰动信号的作用下，与传统的Smith 控制方法相比，本文控制方法仍然具有较好的时间响应特性，而且可以有效地抑制阶跃干扰作用。

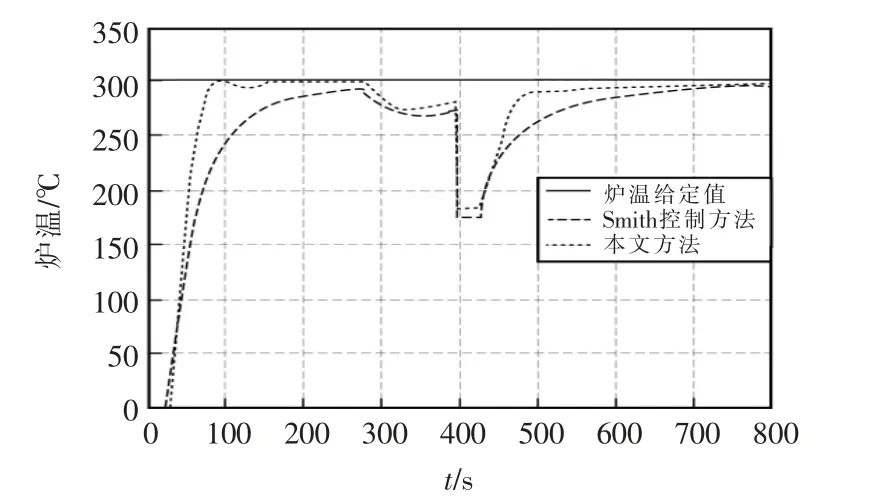
图3 在系统存在扰动时的控制结果Fig.3 Control results in case of system disturbance

若加热炉参数不确定，引起系统模型失配时，被控对象无法追踪原始的参考模型[6]。 当加热炉放大系数K=1.01，引起系统模型失配，控制结果如图4a 所示；当加热炉惯性时间常数T=120，引起系统模型失配，系统控制结果如图4b 所示；当加热炉纯滞后时间τ=30 s，引起系统模型失配，系统控制结果如图4c 所示；当K=1.01，T=120，τ=30 s，引起系统模型完全不匹配，控制结果如图4d 所示；当系统模型完全失配，且在响应时间为250 s 和400 s 时，仍加入阶跃扰动，系统控制结果如图4e 所示。

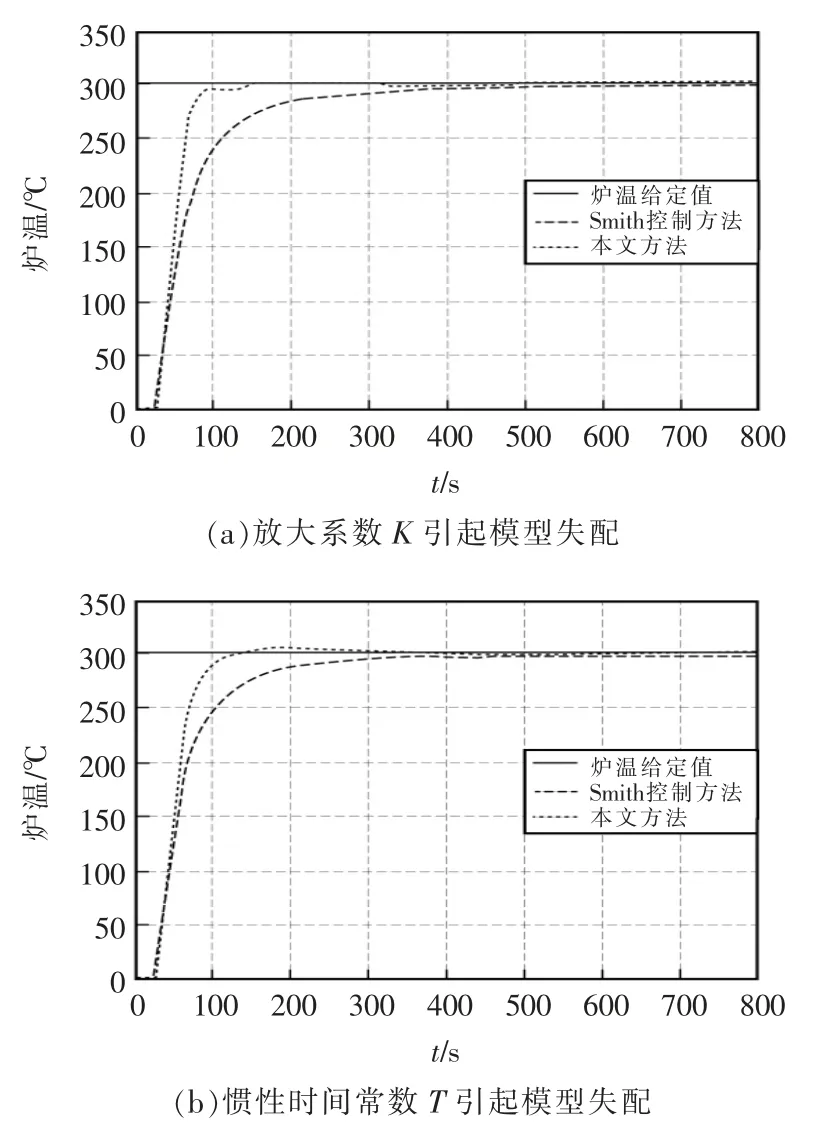
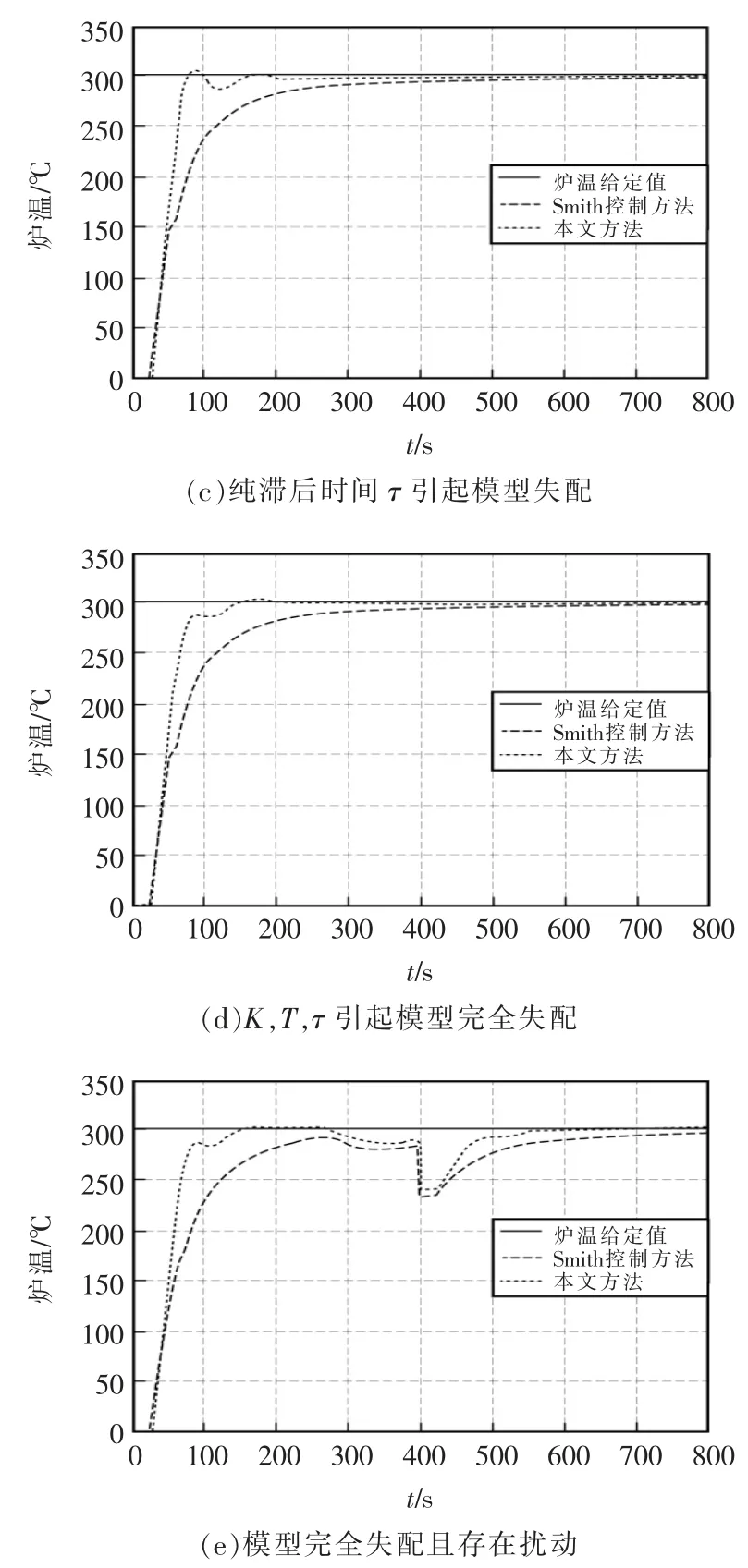
图4 引发模型失配的控制结果Fig.4 Control results of model mismatch

由图可见，当模型失配时，传统的Smith 控制虽然无超调，但系统响应仍然较慢。 当惯性时间常数T、纯滞后时间τ 引起模型失配时，本文方法虽出现了超调，但超调量较小，可以满足系统控制要求。 当模型完全失配，且存在扰动时，本文方法依然可以有效地抑制扰动的作用，从而跟踪阶跃输入。 从整个控制效果来看，本文控制效果优于Smith 控制效果。

5 工程应用效果

根据以上控制器结构搭建加热炉温度控制系统，采用西门子的S7-300 PLC 作为核心处理器，在泰安蔚蓝公司的金属基复合材料铸造生产线进行实际应用。 在此通过温度采集试验验证了所设计控制器的控制效果。 试验采用精密水银温度计对恒定温度场温度值进行标定[7]，在标定的温度值下，测得加热炉温度数据。 具体数据见表2。

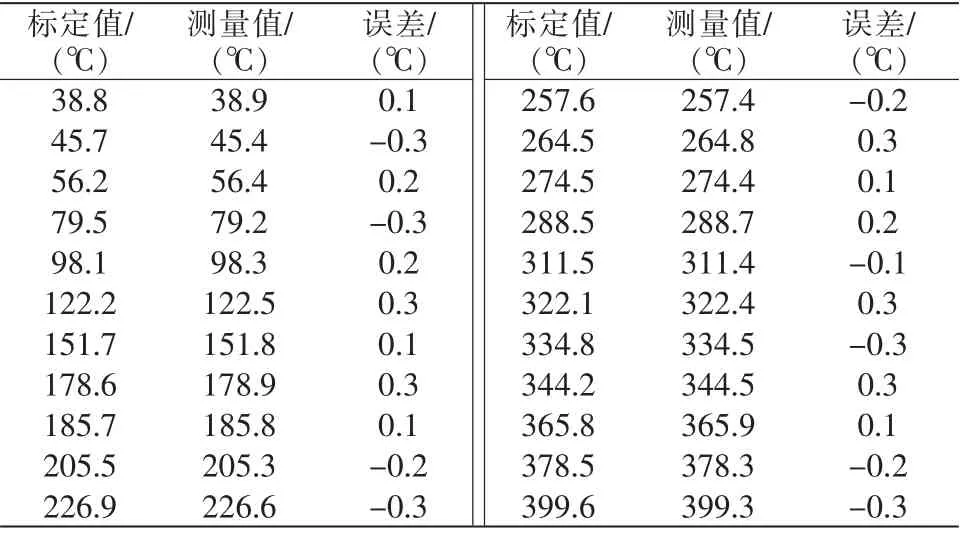
表2 加热炉温度采集试验数据Tab.2 Temperature collection test data of hot press furnace

由表可知，在0～400 ℃温度变化范围内，加热炉温度系统的测量误差为-0.3～0.3 ℃。 这表明加热炉系统在本文所设计的控制器控制作用下具有较好的控制作用，系统测量精度高。

6 结语

本文以铸造、热处理中应用最典型的加热设备加热炉为研究对象，针对加热炉本身的时滞特性设计控制系统结构及相应的控制器控制算法，并分别采用传统Smith 控制和本文控制方法进行对比研究，通过仿真表明，本文控制器算法在控制对象模型失配且存在扰动时，仍具有良好的阶跃跟踪和扰动抑制性能，控制效果明显优于传统的Smith 控制。且经过实际应用， 当温度在0～400 ℃时， 测量误差为-0.3～0.3 ℃，控制精度高，具有一定的应用价值。