架空输电线路脱冰跳跃模拟试验研究

白天明，曹咏弘，薛凯允，关学峰，高玉波

(中北大学 理学院，山西 太原 030051)

0 引 言

输电线路覆冰对电网的安全运行构成威胁，有时尽管覆冰没有破坏塔线体系，但不合理的脱冰方式可能使得导地线跳跃过高，导致导地线闪络跳闸，所以寻求合理的脱冰方式具有重要意义.前期已经通过有限元模拟给出了一个脱冰方案[1]，本文通过实验验证模拟方案的可靠性.

国内外学者针对输电线路覆冰及脱落进行了一系列研究，Jamaleddine等[2]在实验室建立了档距3.22 m的双档导线缩比模型并进行了试验，测量了导线最大跳跃高度，挂点拉力变化以及绝缘子的偏转.Roshan等[3]使用有限元软件ADINA模拟了双跨导线的覆冰脱落，得到了覆冰厚度、跨度、挂点高差对导线脱冰的影响；Morgan等[4]在五档的实际输电线路上通过施加集中荷载模拟覆冰进行试验；László E.Kollár等[5]在线缆上制备了湿雪进行了覆冰，研究了不同的环境条件、液态水含量和雪密度对脱落时间影响；在国内，李宏男[6]在实验室中建立了50 m孤立档的导线进行了导线的跳跃试验，测量了覆冰导线在不同工况下的导线端部张力和导线跨中跳跃高度，并使用有限元软件ANSYS进行了验证.杨文刚等[7]在实验室中模拟了单导线的脱冰状况，得到了不同工况下导线内张力的变化规律.王璋奇等[8]设计了一套新型的导线脱冰震荡模拟测试系统来研究导线脱冰振动，其具有精度高、自动化等优点.谢献忠等[9]设计了缩尺比为1∶20的2档塔线体系试验模型，对拉链式脱冰进行了模拟，得到了脱冰动荷系数和跳跃高度与脱冰工况的关系.姬昆鹏[10]将改进的冰脱落准则用于分析导线受到断裂冲击的情况，并与试验比较验证了方法的可靠性，证明冰脱落效应对导线的动态响应有显著作用.

总的来说，研究输电线路在脱冰响应方面主要有两种手段，有限元模拟和试验；其中试验方法也可以分为两种方法：现场实验和模型试验.

这几种方法各有优缺点，有限元软件模拟更加快捷，成本较低，但有限元模型的误差、算法的误差以及模拟所需的参数难以精确给出，使得模拟结果会有一定的偏差；模型试验，一般在实验室内进行，容易控制变量，可以得到较准确的试验数据，但是可信度低于现场实验.现场实验是在真实塔线结构上进行实验，由于缺乏合适的测试设备和方法，测试难度比较很大，但可信度比较高.

本文在临汾电力学校内的实际输电线路上进行了试验，使用质量块模拟覆冰，研究了不同工况、不同覆冰量的情况下，导线在脱冰过程中的力学响应特性，结果具有较大的参考价值，可以为理论和模拟工作提供参考.

1 试验设计

1.1 实验线路

实验线路为临汾电力学校内一档不通电的输电线路，两端输电塔详细信息如表1 所示.

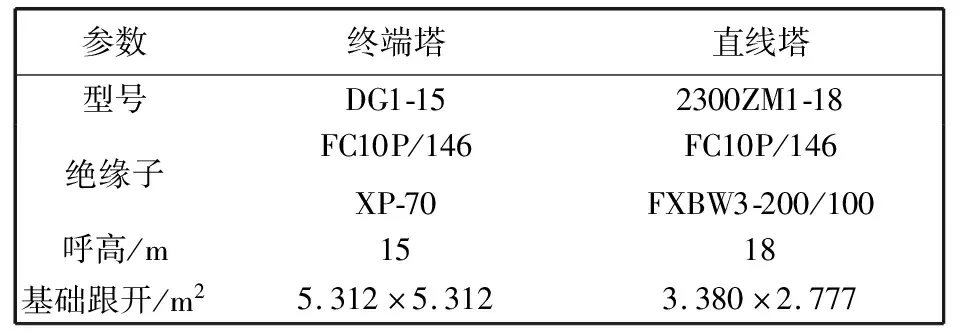
表1 输电塔详细信息

输电线为110 kV双分裂导线LGJ240/30，导线长69.53 m，双分裂导线间距40 cm，在下方导线上进行试验，参数如表2 所示.

表2 测试段导线具体参数

1.2 覆冰模拟系统

如图1 所示，脱冰模拟是通过按一定方式释放导线上悬挂的具有一定重量的质量块来完成.实验中在输电线路上均匀布置12个质量块共4组，挂点间距4.6 m.

图1 悬挂重物示意图

1.3 位移测试系统

位移通过拉线位移传感器进行测试，测点位于试验线路的中点，如图1 所示.测量装置及安装如图2 所示.

图2 测试系统

为了测量导线测点水平位移和垂直位移，在测点布置了两个拉线位移传感器，一个竖直向下，一个呈30°夹角斜向摆放，可以得到导线测点的水平位移和竖直位移.

1.4 覆冰脱落控制系统

各种脱冰工况是通过电磁铁控制重物按照一定时序脱落来实现的，控制系统如图3 所示，根据脱冰工况所需调整接线器接线方式来控制脱冰.

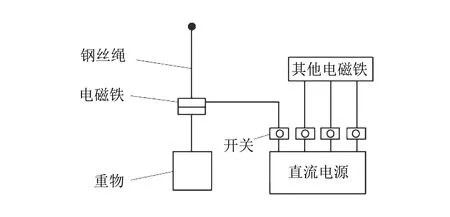
图3 控制系统

1.5 工况设置

为了研究不同工况下的动力学响应，设计了覆冰同时脱落、先两端后中间、先中间后两端、顺序脱落等7种覆冰脱落工况，如表3 所示.

表3 脱冰工况设置

2 测量和分析

实测了单个重物分别为2.5 kg，3.5 kg，5 kg的3种覆冰工况，共21种脱冰工况.

2.1 静力加载

图4 为单个重物为2.5 kg的覆冰工况，逐步顺次加载12个重物时测点的位移图.可以看出，随着载荷的增加，静载位移与载荷增加基本成正相关，导线的弧垂也与导线施加载荷成正相关.

图4 加载中导线测点位移时程曲线

2.2 脱冰响应

以工况1为例，不同载荷作用下的时程曲线如图5 所示.

图5 不同载荷下卸载导线测点位移曲线

由图5 可以看出，相同脱冰工况时，不同覆冰工况的脱冰响应规律类似，衰减时间相同，但是跳跃高度随载荷增加而增加，因此以下以单个重物为2.5 kg的覆冰工况为例来分析说明.

以工况1为例，其位移时程曲线如图6 所示.

图6 导线测点竖向位移和水平位移的比较

由图6 可以得到，导线的振动周期为1.85 s，脱冰后，导线首先做衰减振动，振幅不断减小，之后由于相邻档的导线振动影响，出现二次振动，振动衰减时间较长，大约为34 s，水平位移始终保持在较小的水平，主要是由于绝缘子串横向摆动引起的.

针对不同工况进行分析，得到不同工况的位移曲线，如图7 所示.

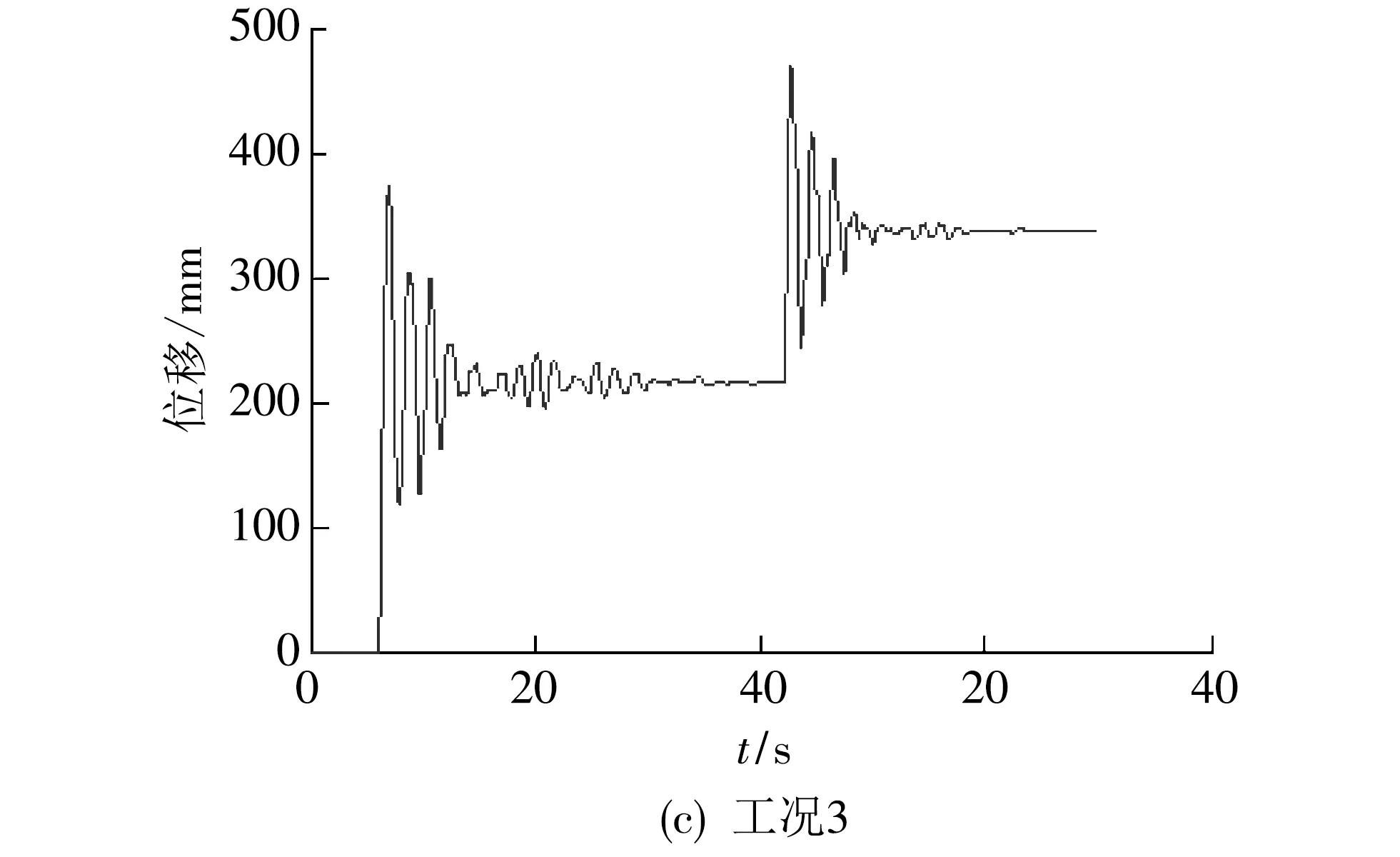
图7 不同卸载工况测点位移曲线

分析各种工况，得到每个脱冰工况下各个步骤的跳跃高度，如表4 所示.

表4 不同工况各个步骤测点最大位移

对比工况2和3，得到中间荷载先卸载比两端荷载先卸载具有更大的跳跃位移，因而更容易发生闪络事故，所以在实际脱冰时，需先考虑边缘脱冰，其次考虑中部脱冰；对比工况2和7，得到端部载荷的分步卸载有利于减小导线的跳跃高度；对比工况2和6，得到了中间荷载的分步卸载，同样减小了导线的跳跃高度；因此在实际脱冰中，档内脱冰，端部和中间段覆冰均需分步进行.

3 模拟部分

3.1 结果对比

在有限元软件ABAQUS中建立了单耐张段3塔4线塔线体系模型如图8 所示，对相关脱冰工况进行了模拟，图8 为一些工况模拟和实验工况的数据对比.

图8 塔线模型

图9 模拟和实验的数据对比

对比这两种工况，模拟数据的规律和实验基本相同，第一个波峰高度，也即最大脱冰跳跃高度基本一致，但模拟中周期为2 s，略大于实验数据，这是由于在模拟导线时采用了杆单元忽略了导线的弯曲刚度[11]所导致的.在档距增大的情况下，其影响会缩小[12].

该对比验证了实验方法以及模拟方法的可靠性.

3.2 质量块模拟覆冰的可靠性分析

对覆冰12.5 mm全脱的工况进行了模拟，对比质量块和均匀覆冰的两种荷载情况下的中点位移，如图10 所示.

图10 均匀覆冰和质量块载荷的中点位移比较

通过对比可以看到，曲线基本重合，所以使用质量块可以用于模拟均匀覆冰的情况.

3.3 覆冰量对跳跃高度的影响

实验中使用质量块虽然可以模拟不同覆冰量的覆冰[13]，但由于实际情况所限，只能采用几种荷载进行试验.为了更好地拟合数据，在有限元中模拟了更多不同荷载下全部脱冰工况的导线最大跳跃高度，结果如图11 所示.

图11 跳跃高度随覆冰量的变化曲线

通过拟合模拟数据得出

y=0.118x-0.001 84x2-0.026 1,

(1)

式中：y为全部脱冰工况的跳跃高度，m；x为覆冰量，mm.公式拟合残差平方和为0.003 37，与模拟拟合效果较好.结果表明，在档距固定的条件下，全部脱冰工况的脱冰跳跃高度和覆冰量之间为二次关系.

4 结 论

1)在实际的脱冰问题中，须先在端部分步脱冰，其次在中间分步脱冰，可以有效地减小跳跃高度.

2)不同负载情况，相同脱冰工况导线的脱冰响应规律基本相同，幅值成正相关，覆冰量越大，导线脱冰振动幅值越大，满足式(1).

3)模拟和试验的位移曲线规律相同，验证了模拟方法的正确性，为模拟工作提供了参考.