基于张量分解的间歇过程故障诊断方法
张晓玲, 曹玉苹, 邓晓刚
(1.中国石油大学 胜利学院, 山东 东营 257097;2.中国石油大学(华东) 控制科学与工程学院, 山东 青岛 266580)
1 前 言
间歇生产方式在现代工业界所占比重越来越高,其过程监控和故障诊断也引起广泛关注[1]。长期以来,过程监控的主流统计方法[2-5]如主元分析(principal component analysis, PCA)、偏最小二乘(partial least squares, PLS)、独立元分析(independent component analysis, ICA)、典型相关分析(canonical correlation analysis, CCA)等在应用于间歇过程故障诊断时,都是采用将三维多批次历史数据展开成二维的多向(multi-way)处理方法,即使针对间歇过程的不同特点涌现出一系列改进算法[6-14],也大都对数据进行展开处理,如按批次展开、按变量展开成二维矩阵的方式等。此类多向展开的处理方法将三维多批次数据中每一批次的二维矩阵展开变成向量看待,势必会破坏原有数据的相关性,导致部分信息的丢失和特征不完全提取。
近年来,一些基于张量的数据降维方法,如张量PCA (tensor PCA, TPCA)[15-16]、张量邻域保持嵌入算法(tensor neighborhood preserving embedding, TNPE)[17]等,使用张量模式的特征提取方法对张量形式的数据进行特征提取,保证了张量形式的特征空间不被破坏,张量分析逐渐在计算机视觉、图像处理、模式识别等领域成为研究热点[18]。本文借鉴以上方法中张量分析的思想,对间歇过程在线监控时,将三维数据的每一批次看作一个二阶张量,应用TPCA算法对三维数据直接提取特征信息,不破坏三维样本中每一批次的原始矩阵空间结构,并定义R2统计量和SPE统计量建立故障检测模型;另外,为能更及时检测出间歇过程中常出现的渐变故障(如间歇精馏过程中催化剂活性的缓慢变化、间歇反应釜换热器由于长时间使用结垢现象越来越严重而导致换热性能的逐渐下降),本文利用累积和控制图(cumulative sum,CUSUM)分析思想,将其应用于 TPCA算法中,提出累加和的张量主元分析(summed tensor principal component analysis, STPCA),将三维历史数据按一定的滑动窗口累加求和,累积历史信息,再做TPCA算法处理,建立故障检测模型,从而提高对渐变故障在初始出现阶段检测的灵敏度。
2 TPCA方法

可通过以下迭代方法实现式(1)中U、V的求解:
Step2:设置循环变量n初始值为1,进入循环迭代运算。
Step4:对CY1进行特征值分解得到特征值矩阵Λ和特征向量矩阵Vn+1,只选取前J'个最大的特征值组成,Vn+1则是由前J'个特征值对应的特征向量矩阵。
Step5:令Y2m=XmVn,求Y2的协方差阵
Step8:输出最终的U∈RK×K'、V∈RJ×J'。
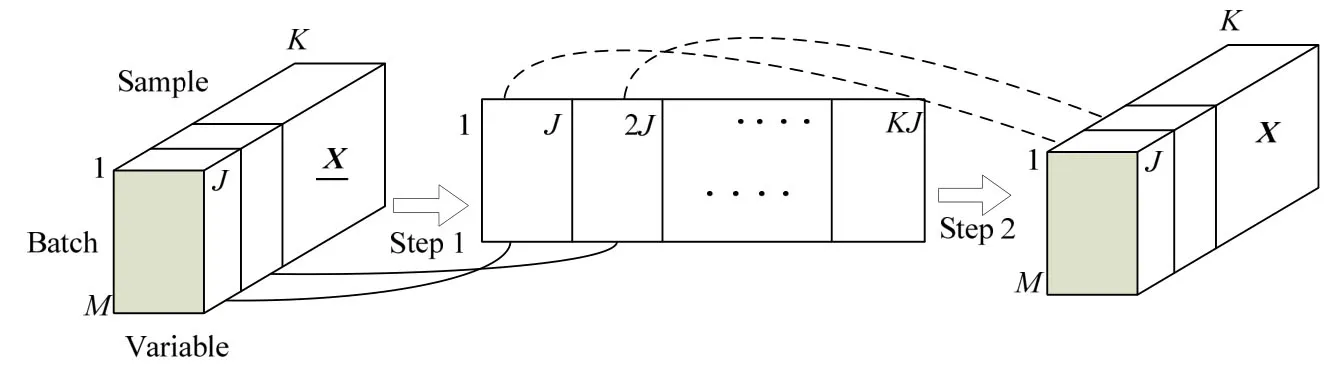
图1 三维数据预处理Fig.1 Schematic diagram of three-way dataset preprocessing
注意,TPCA变换处理的数据X是经过标准化处理的,其处理过程如图1所示,第1步将初始数据展开成大小为M×KJ的二维矩阵,沿着每列进行均值为0方差为1的归一化处理,第2步再恢复成三维结构数据X(M×K×J)。此处的展开仅用于数据的预处理,应用TPCA变换时使用的仍是三维矩阵X(M×K×J)。因此,预处理后的三维数据X(M×K×J)通过以上Step1~8的迭代算法获得U和V后,经过映射公式Ym=UTXmV,则可被投影到低维张量特征空间得到Y(M×K'×J' ) = {Ym∈K'×J',m= 1,2,… ,M}。
3 基于STPCA方法的间歇过程故障诊断
3.1 STPCA算法
各类间歇过程中的渐变故障很常见,渐变故障是某变量操作值缓慢偏离正常变化区间、不断累积的过程,故障初期变化量较小,很多故障检测方法对该类故障存在预报大大延迟的问题。为提高检测故障灵敏度,本文利用PAGE等[19]提出的累积和(CUSUM)控制图思想,提出一种基于累加和的张量主元分析算法(STPCA),将经过预处理后的正常批次数据X(M×K×J)按照每批次内滑动窗口大小进行历史信息的叠加,数据处理公式如下:
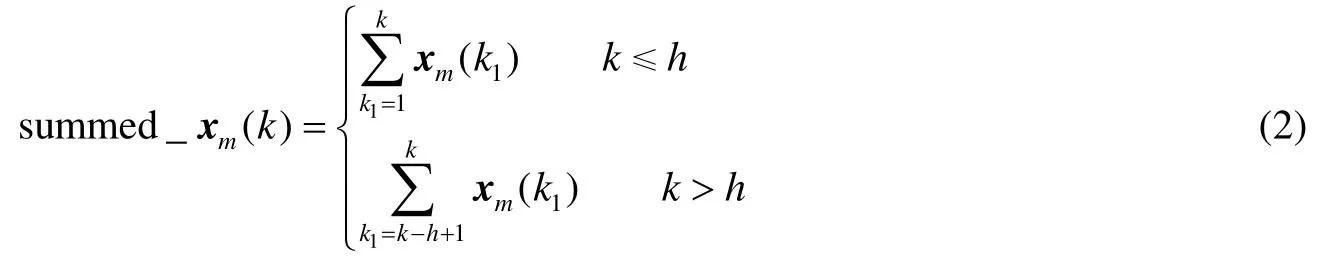
summed_xm(k)表示第m批次中按照式(2)累加和后的第k采样时刻观测值,h为累加求和的宽度,构成移动的滑动窗口,当k>h,每一时刻的数据值都由前h个多变量样本求和得到,从而得到求和后的summed_X(M×K×J) = { summed_Xm∈RK⊗RJ,m= 1 ,2,…,M},然后用第1节中TPCA算法对其进行特征提取,求得变换矩阵U和V,为下一步故障诊断打下基础。
3.2 基于STPCA算法的在线监控
在线监控过程主要包含2个阶段。
第1阶段:离线模型的建立
② 对X(M×K×J)按式(2)进行累加和处理,获得summed_X(M×K×J)。
③ 运用 TPCA算法,确定投影矩阵U∈RK×K'和V∈RJ×J',计算经过投影后的低维张量特征空间数据Y={Ym∈RK'⊗RJ',m= 1,2,… ,M} ,Ym是累加和处理后summed_Xm的低维投影,变换公式为:Ym=UT* s ummed_Xm*V。
④ 建立故障检测模型。
对基于TPCA和STPCA 2种算法的间歇过程故障检测,本文都采用 R2和SPE统计量。
R2是基于支持向量数据域描述(support vector domain description,SVDD)[20]方法建立的统计量,表示每批次Xm的投影Ym到特征空间中心的距离,其计算式如下[21]:

拉格朗日乘子iα通过下式的最大化问题求解[21]:

C为惩罚因子,可取1。
SPE统计量用来测量残差空间的变化。先通过U、V重构summed_Xm的估计值,得到残差矩阵从而得SPE统计量的计算式:

R2和SPE统计量皆可通过核密度估计法[22]确定各自95% 或99% 的置信限(也称控制限、阈值),在每个采样时刻k分别利用核密度估计法计算对应采样点所有批次统计量的阈值,因此可得到动态变化的控制限,当统计量超出各自控制限所判定的正常变化范围,则意味着故障的出现。
第2阶段:在线故障检测
①采集新批次第k采样时刻数据根据离线建模标准化处理时得到的均值和方差进行预处理。
②对预处理后的数据xnew,k按照式(2)进行累加求和处理,得到 s ummed_xnew,k。
③计算新的投影矩阵和残差:

其中uk表示矩阵U中的第k行向量。
④参考式(3)和(5)分别计算新的在线2R和SPE统计量,得到

并判断统计量是否偏离各自阈值,以确定间歇过程运行状况。
4 仿真结果分析
分批补料的盘尼西林发酵过程是典型的间歇式生产过程,本文基于BIROL等[23]开发的标准仿真软件Pensim 2.0产生的盘尼西林发酵数据进行在线监控算法仿真研究。本仿真由该软件在正常操作范围内对初始条件加入一定的微小偏移和适当噪声生成30批次数据作为训练样本,每批次含11个观测变量,反应时间相等,均为400 h,采样间隔为0.5 h,从而得到用于建立MPCA、TPCA、STPCA监控模型。另外,利用Pensim2.0产生6个故障批次,表1是3种跳变故障,表2是渐变类型故障。

表1 跳变故障Table 1 Step faults used for detection

表2 渐变故障Table 2 Gradual faults used for detection
建模时,3种方法都需要对数据进行标准化,不同的是,MPCA方法如图1中Step 1按批次展开成二维,按列作归一化处理,得到二维矩阵X(30×8800),即X(M×KJ),在此基础上建立MPCA模型。TPCA和STPCA算法则需将标准化后的二维矩阵X(30×8800)再按图1中Step 2还原成X(30× 8 00×11),在保持和不破坏原来每批次数据结构基础上建立各自的监控模型。因此,传统PCA算法会把每批次的数据Xm∈RK⊗RJ转换为向量xm∈RKJ看待,特征值分解的矩阵大小是KJ×KJ,基于张量的 TPCA方法其特征值分解的矩阵大小仅为K×K或J×J,在特征值分解计算复杂度上要更低。另外,STPCA相比TPCA方法在数据处理上多一步累加和处理,以增大对渐变故障检测的灵敏度。最后的监控模型所用到统计量也有差异:MPCA使用T2和SPE,TPCA和STPCA则运用本文定义的 R2和SPE统计量。

图2 基于MPCA方法的故障1检测结果Fig.2 Fault 1 detection results based on MPCA
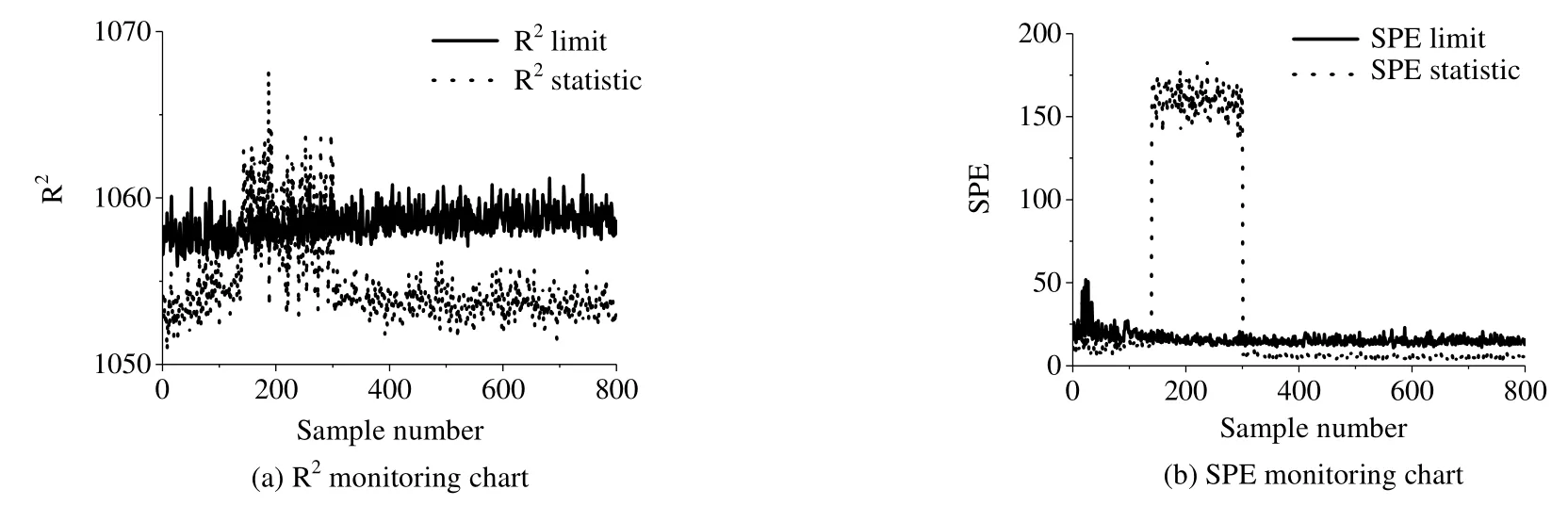
图3 基于TPCA方法的故障1检测结果Fig.3 Fault 1 detection results based on TPCA

图4 基于MPCA方法的故障2检测结果Fig.4 Fault 2 detection results based on MPCA
当新批次中出现故障 1、2、3跳变故障时,基于 MPCA的在线故障检测结果如图2、4、6所示,MPCA的SPE统计量能准确预报故障的发生(140~300采样点),但在非故障时段有较高误报,从图中可明显看到有多点超出控制限,特别是对故障3达到了5.12% 的误报率(见表3)。相对而言,图3、5、7所示TPCA故障检测结果中,SPE统计图既能准确检出故障,又具有较低误报率,由表3可见,对前两个故障的误报率为0,仅对故障3有约1.63% 的误报,但仍低于MPCA方法的结果。与SPE统计量相比,MPCA方法的T2统计图检测效果较差,只能对故障1有效,对故障2和3完全不敏感,无任何超限警报;反观TPCA方法的 R2统计图,在采样点140~300仅无法检测出故障3,能完全准确检测到故障2,对故障1仅有少量点的漏报。从误报率情况分析,TPCA的 R2统计量也优于MPCA的T2统计量。总体分析,TPCA两种统计图对3个故障的检出率高于 MPCA方法,且具有较低的误报率。可见,将利用张量分解直接处理三维数据的TPCA方法引入到间歇过程故障检测中,构造 R2和SPE统计量进行实时监控是可行并具有一定效果的。

表3 MPCA和TPCA方法的故障检测误报率对比Table 3 Comparison of false positive rates (FPR) by MPCA and TPCA
图5 基于TPCA方法的故障2检测结果Fig.5 Fault 2 detection results based on TPCA

图6 基于MPCA方法的故障3检测结果Fig.6 Fault 3 detection results based on MPCA

图7 基于TPCA方法的故障3检测结果Fig.7 Fault 3 detection results based on TPCA
为提高检测渐变故障的灵敏度,本文在TPCA基础上提出基于STPCA的间歇过程故障诊断方法,同样使用 R2和SPE统计图进行故障分析。仿真实验设置了表2所述3种故障,分别是通风速率、搅拌功率、底物流加速率从第200采样点以一定速度呈现斜坡变化,模拟间歇过程中可能出现的渐变类故障。图8到图13反映了MPCA、STPCA方法对3个故障批次的检测效果。
从图8、10和12所示结果观察,MPCA的T2和SPE统计量均在一定时刻越过阈值不断增加,表明渐变型故障的发生;同样,图9、11、13中STPCA方法的统计结果图也给出了故障警报。但明显的是,两种方法的SPE统计图比基于得分的T2和基于特征空间的 R2统计量趋于更灵敏,给出故障预报要早。为直观对比不同方法的检测效果优劣,本文通过表4列出两种方法各统计量所确定的故障出现时刻,并假设统计量连续8个采样点超过控制限则认定该采样时刻为故障检测点。对比SPE统计量,针对渐变故障4、5、6,STPCA分别领先MPCA方法9个、28个、30个采样点提前给出故障指示;STPCA的2R统计图检测故障的能力虽逊于SPE统计量,却仍比MPCA的2T统计量分别早117、336、56个采样时刻超出控制限。综合看来,两种方法检测渐变故障时,相对故障实际发生时刻都有或多或少的滞后,原因在于故障变量刚开始是缓慢变化的,偏离正常范围需要一定的时间间隔,只有当变量值渐渐漂移累积超出一定量后,监测系统才能判断过程出现了非正常的变化。但STPCA方法将历史批次数据进行叠加处理,放大故障变量的初始偏移,并在张量空间进行特征值分解、不破坏原有数据结构基础上得到监控统计量,结合以上结果图和表4,不难看出该方法能更早检测出渐变故障,体现该方法的优越性。
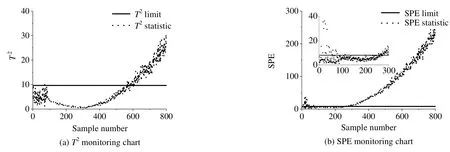
图8 基于MPCA方法的故障4检测结果Fig.8 Fault 4 detection results based on MPCA

图9 基于STPCA方法的故障4检测结果Fig.9 Fault 4 detection results based on STPCA

图10 基于MPCA方法的故障5检测结果Fig.10 Fault 5 detection results based on MPCA

图11 基于STPCA方法的故障5检测结果Fig.11 Fault 5 detection results based on STPCA

图12 基于MPCA方法的故障6检测结果Fig.12 Fault 6 detection results based on MPCA

图13 基于STPCA方法的故障6检测结果Fig.13 Fault 6 detection results based on STPCA

表4 MPCA和STPCA检出的故障发生采样点Table 4 Fault sampling points based on MPCA and STPCA
需要说明的是,STPCA方法更适用于渐变故障存在的场合,尤其是故障出现早期,通过CUSUM累积过程中的微小变化,提高对渐进、缓慢变化类故障初期较小故障偏移的检测。同时,该方法中累加求和宽度h的取值与检测效果关系密切,若h取值太小,利用 CUSUM 累积的历史信息不够丰富,对渐变故障出现初期检测准确率会较低,反之一味追求快速检测出故障而将h取得过大,会因带入部分噪声信息而增加误报率,导致故障检测效果下降。目前总体上,h大小的选择没有统一标准,多是根据经验或交叉验证方法确定。本文通过反复试验,选择适当的h值,既能提高对渐变故障的检出率,较早发出故障报警,又防止出现较高误报的情况。另外,STPCA算法在故障检测时,对新批次数据引入CUSUM的处理,不可避免会产生故障检测延时,因此,本方法并不适用于故障检测实时性要求较高的场合。
5 结 论
传统将三维数据变成二维的间歇过程故障诊断方法,破坏数据原有的空间结构和相关特性,必然会对过程监控效果产生不利影响。本文将基于张量分解的TPCA算法引入到间歇过程监控中,直接将三维数据作为张量目标进行运算,保留了数据完整性,定义2R 和SPE统计量建立故障检测模型。经仿真验证,基于TPCA的间歇过程故障诊断方法适合检测突变故障,检测效果较好。针对间歇过程中常发生的渐变故障,本文提出STPCA方法,通过对三维数据多个连续时刻的采样值求和,不断放大历史信息,同时又保证不破坏三维原始数据结构,因此在检测渐变类型故障的仿真实验中,STPCA方法有更好效果,提高故障检测灵敏度,相应降低了漏检率。
符号说明:


