平面波输入下海水-海床-结构动力相互作用分析1)

陈少林 孙 杰 柯小飞

(南京航空航天大学土木与机场工程系,南京 210016)

引言

随着我国海洋战略的实施,将要建造大量近海工程结构,如何保证近海工程结构在服役期的地震安全性是目前面临的重要科技问题.要保证近海工程结构的地震安全性,首先要对其在潜在地震作用下的反应进行准确的分析预测[1-9].目前,受水下振动台设备的限制,采用试验方法对海工结构的地震反应分析还很少.而在数值分析方面,其属于半无限域地震波散射问题(如图1 所示),涉及到海域场地自由场分析(为散射问题提供输入)、海水-饱和海床-结构间的相互耦合分析,以及半无限海域场地的人工边界条件,问题十分复杂.

图1 海洋工程结构地震反应分析示意图Fig.1 Seismic response analysis of marine engineering structure

其中,海水、饱和海床、结构间的流固耦合问题,若采用常规的流固耦合求解思路,须分别采用流体声波方程、饱和多孔介质方程和固体波动方程的求解器,各求解器在每一时步进行界面耦合,十分不便,目前还没有成熟方法和软件能高效地解决此问题.因此,发展一种海洋地震工程中海水-饱和海床-结构耦合分析的高效方法,考虑海床的非线性,揭示强震作用下海床液化失稳机理和海工结构的灾害模式十分必要.

对于海域场地非线性地震响应分析,可以采用等效线性化分析方法[10-11]或时域非线性分析方法[12-18].一般认为,等效线性化方法适合于弱非线性,对于强非线性,宜采用时域非线性分析方法.当采用时域非线性方法分析场地地震响应时,需要先进行水平成层场地的自由场分析,作为边界的输入.目前,一般采用传递矩阵方法[19-21]进行自由场分析,适合于线性或等效线性化情形,可以考虑地震波斜入射;也可采用有限元数值分析方法[22-24],根据Snell定律,将二维自由场分析一维化,采用数值方法实现一维分析,再根据视速度将一维波场外推至二维、三维,这种外推只适合于波速恒定的线性情形.因此,若采用数值方法求解非线性自由场,只能获得一维自由场,即垂直入射情形.在考虑饱和海床的非线性时,理论上,自由场计算也需采用与内域计算同样的本构,若与内域分析的本构不一致,对结果的影响值得讨论.

本文在海域场地自由场分析[20]和海洋地震工程流固耦合问题统一计算框架[25-26]的基础上,首先考虑饱和海床的非线性,分析海域场地的非线性反应特征,并讨论了采用线性自由场和非线性自由场对结果的影响.进一步分析了海域场地和海水-海床-结构体系在地震作用下的动力响应,对比了线性海床和非线性海床情形时响应的差异,为海洋工程结构的抗震设计提供理论基础和分析手段.

1 基本理论

如图2 所示,从场地中截取有限土体,采用八结点三维实体单元对其进行空间离散,整个计算区域的有限元节点可以分为两类:内节点与人工边界节点.内节点又分为一般内节点(包括自由表面节点)与不同介质交界面上的界面节点.场地介质为饱和多孔介质,海水、基岩均可视为饱和多孔介质的特殊情形.

图2 场地-结构相互作用分析模型示意图Fig.2 Site-structure interaction analysis model

1.1 一般内节点运动

对于饱和多孔介质,其固相平衡方程[27-28]

液相平衡方程

相容方程(考虑初始孔压和初始体应变为零时)

其中,Ls,Lw为微分算子矩阵,σ′为有效应力矢量,τ为平均孔压,P为孔隙水压,为固、液相的速度,为固、液相的加速度,ρs,ρw分别为固、液相的密度,β 为孔隙率,b=β2µ0/k0,k0为流体渗透系数,µ0为动黏度系数,Ew为流体的体变模量,es,ew分别为固相和液相的体应变.

以上方程当孔隙比β=1 时,可退化为理想流体方程;当孔隙比β=0 时,可退化为弹性波动方程.因此,流体、弹性固体、饱和多孔介质可统一由广义饱和多孔介质(0 ≤β ≤1)方程描述,仅是材料参数不同.因此,海域场地中地震波传播问题可由广义饱和多孔介质方程统一描述.

对方程(1)和(2)采用伽辽金方法离散,并考虑相容方程(3)及边界条件,可得任一结点i的运动平衡方程为[26]

其中,Msi,Mwi分别为固、液相质量;分别为固、液相本构力,本文采用Davidenkov 模型考虑固相的非线性,具体见1.4 节;分别为固、液相黏性阻力;分别为固、液相边界力,当节点i为一般内节点时,界面力为零.

对式(4a),(4b)进行时步积分,可得到一般内节点i的固、液相位移递推公式

1.2 界面节点运动

对于界面节点,如图2 中的j(k),根据文献[26],采用隔离体概念,对式(4a),(4b)进行时步积分得

其中,i=j,k

由式(6)、式(7),以及界面连续条件,经推导,可得

其中

1.3 人工边界节点运动

为了有效地模拟外行波穿过人工边界的运动状态,我们采用多次透射公式[29]

该局部人工边界条件具有普适性,与具体波动方程无关,可直接用于饱和多孔介质中的波动[30].分别将式(11)应用于广义饱和多孔介质的固相和液相位移,可得到边界点在p+1 时刻的散射波场位移,再叠加上边界点的自由场位移,即可得到边界点的固、液相总位移.

1.4 饱和土骨架非线性

在强震作用下,土体将进入非线性,本文采用三参数的Davidenkov 本构模型,通过对饱和土体固相剪切模量实时修正,可以较为有效地描述饱和土体的非线性动力特性[14-15].

由Martin 和Seed[18]提出的Davidenkov 本构模型骨架曲线的表达式为

式中,τ,γ 分别为剪应力、剪应变;Gmax为初始剪切模量;A,B,γ0可由土体动三轴实验数据进行拟合得到.

经Masing 法则修正后滞回曲线如图3 所示,依据Pyke 提出的“n倍法”,应力-应变滞回曲线服从下述关系

分别对式(13)、式(15)求导,可得到初始骨架曲线段、滞回曲线段的时变切线剪切模量

图3 不规则加卸载准则修正的Davidenkov 本构模型曲线Fig.3 Davidenkov mode modified by irregular loading and unloading criterion

式中参数(2nγ0)2B根据当前拐点及历史上最大(小)点确定.上述本构模型是依据实验室得到的主空间上的主剪切应力-主剪切应变曲线而建立的,通常假定该本构模型同样适合于复杂三维情形的主剪切应力-主剪切应变关系,因此将其用于三维计算分析时,需根据应变分量,求出主剪切应变,再根据式(16)和式(17)更新剪切模量.

2 算例分析

2.1 自由场对海域场地非线性响应的影响

考虑如图4 所示的三维海水-饱和土-基岩海域场地模型,整体尺寸为62 m×62 m×60 m,单元尺寸为1 m×1 m×1 m,各层介质参数如表1 所示.其中,饱和土层采用三参数的Davidenkov 非线性本构模型,参数A=1.1,B=0.2,γ0=0.000 4;海水层和基岩层考虑为线性.考虑SV 波垂直入射,输入如图5所示的单位脉冲,步距为0.000 2 s,步数为8000 步.

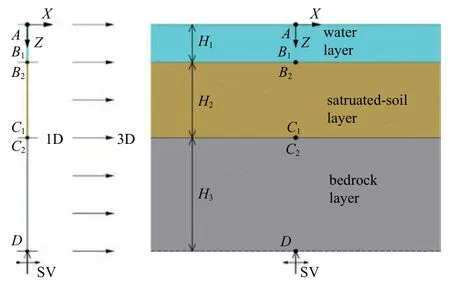
图4 海水-饱和土-基岩场地模型示意图Fig.4 Water-saturated soil-bedrock site model

表1 模型参数Table 1 Parameters of the model

图5 脉冲时程图Fig.5 Pulse time history

分别采用如下两种方案计算自由场:(1)方案I采用传递矩阵方法,得到线性自由场;(2)方案II 采用一维有限元方法,饱和土层采用Davidenkov 非线性本构模型,参数与三维模型相同,底边界采用透射边界,得到非线性自由场.将自由场作为输入,并在5个边界面(左、后、右、前、底)上施加透射边界,进行三维非线性海域场地分析.

理论上,本模型为水平成层场地,SV 波从底部垂直入射,忽略海水黏性,因此SV 波不能在海水层传播,海水层X向位移应为0.从图6(a)、图6(b)中可以看到,方案II 海水层表面A点X向位移为0,与理论相符;而方案I 中,A点X向位移明显,幅值量级与输入脉冲波相同,与理论不符.

图7 为方案II 中,一维与三维模型中饱和土层和基岩层各监控点(见图4)的响应,从图中可以看出,一维模型和三维模型的响应完全一致,验证了非线性自由场输入的可靠性.

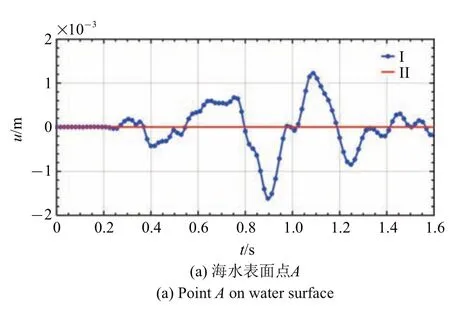
图6 方案I、II 海水层监控点X 向位移对比Fig.6 Comparison of X-direction displacement of water layer monitoring points in scheme I and II

图6 方案I、II 海水层监控点X 向位移对比(续)Fig.6 Comparison of X-direction displacement of water layer monitoring points in scheme I and II(continued)

图7 方案II 一维模型与三维模型X 向位移对比Fig.7 Comparison of X-direction displacement between 1D model and 3D model in scheme II

2.2 海域场地非线性响应特性分析

采用与2.1 节中相同的模型、脉冲输入,分别考虑饱和土层线性和非线性情形,分析饱和土层非线性对海域场地响应的影响.

对于线性情形,SV 波在场地中的传播过程如图8 所示,根据基岩层剪切波速c3和土层剪切波速c2估算各波峰到时,Δt3=H3/c3=0.075 0 s,Δt2=H2/c2=0.084 4 s.

图8 SV 波传播过程示意图Fig.8 Schematic diagram of SV wave propagation

根据文献[31-32],得SV 波垂直入射时,略去高阶项后,基岩层-饱和土层分界面上行波反射系数

其中波阻抗比ψ=ρ2c2/(ρ3c3),ρ2=ρs2(1 -β2),ρ3=ρs3,得R1=0.547.

上行波透射系数

得基岩分界面处透射系数为T1=1.547;基岩层-饱和土层分界面下行波反射系数

其中波阻抗比ψ′=ρ3c3/(ρ2c2),得R2=-0.547;下行波透射系数

得基岩分界面处透射系数为T2=0.453;类似地,得饱和土层-海水层分界面上行波反射系数为1.

表2 与表3 对波峰到时及幅值的实际值与理论值进行对比,结果误差较小,证明了线性情形模拟准确.

考虑饱和海床为非线性时,当SV 波传至饱和土层时,土骨架进入非线性状态,剪切模量G2减小,则剪切波速c2减小,因此波阻抗比ψ 减小,且0 ＜ψ ＜1,根据式(18)、式(19),反射系数R1增大,透射系数T1也增大,因此图9 中波峰2′,3′,4′峰值比线性情形的要大;图9(a)中波峰5′峰值本应随波峰3′峰值增大而增大,但由于饱和土层非线性阻尼效应的影响,峰值反而减小;同时,由于剪切波速c2减小,图9 中波峰5′,6′,7′,8′到时相比线性情形有延迟;另一方面,剪切波速c2减小,则ψ′增大,且ψ′＞1,根据式(21),基岩层-饱和土层交界面下行波透射系数T2减小,再加上饱和土层非线性的阻尼效应的影响,波峰6′,7′,8′峰值减小明显.

此外,对于饱和土层液相,黏性力与惯性力相比,占主导作用.因此,图9(b)和图9(d)中液相位移时程表现为明显的扩散过程.

2.3 场地-结构模型

考虑如图10 所示的三维场地-结构模型,场地尺寸为62 m×62 m×60 m,桩总长60 m,海水以上部分长10 m,截面尺寸为4 m×4 m,上部承台尺寸为6 m×6 m×6 m.单元尺寸为1 m×1 m×1 m.饱和土层分别按线性、非线性两种情形计算,场地、桩和承台参数见表1.输入图5 所示的的SV 脉冲波.

表2 波峰到时Table 2 Arrival time of wave crest

表3 波峰幅值Table 3 Amplitude of wave crest

图9 线性和非线性情形各监控点X 向位移对比Fig.9 Comparison of X-direction displacement of monitoring points in linear and nonlinear cases

图9 线性和非线性情形各监控点X 向位移对比(续)Fig.9 Comparison of X-direction displacement of monitoring points in linear and nonlinear cases(continued)

图10 三维场地-结构模型示意图Fig.10 3D site-structure model

由于桩与结构的存在,桩的运动会弓起海水的运动,从图11(a)和图11(b)中可以看到,海水层存在一定位移.

从图11(c)～图11(f)可以看出,相比线性情形,非线性情形饱和土层位移幅值要小,衰减更快;非线性情形基岩层位移主要是初始的入射波及其在基岩层-饱和土层界面的反射波,来自饱和土层的透射波幅值很小,原因与2.2 节中的分析相同.

从图11(g)～图11(j)可以看出,由于饱和土层位移影响,非线性情形承台顶部、桩上部位移幅值要比线性情形小.从图11(l)可以看出,由于基岩层位移影响,非线性情形桩底部0.3 s 后位移较小.

根据桩单元节点的位移,可以得到不同高度处桩水平截面上的剪力和弯矩,如图12 所示.从图中可看出,非线性饱和海床与线性饱和海床情形相比,沿桩身的最大剪力和最大弯矩整体上要小.无论是线性还是非线性情形,桩头的弯矩(-10 m 处)均较大,且在土层界面(10 m 和30 m 处)附近弯矩为极大值,桩端附近弯矩也较大.

本算例中饱和土层厚20 m,在饱和土层中间处水平截取一个平面,监控该截面不同时刻的孔压.图13 为饱和土层为非线性情形下,SV 波垂直入射时,不同时刻该截面的孔压云图.

考虑SV 波沿X–Z平面垂直入射时,主要反应为X方向,由于模型对称,则位移关于桩基X轴、Y轴对称分布.孔压值主要受速度散度变化的影响,孔压的分布关于桩基X轴对称,关于Y轴反对称分布,如图13 所示.经计算地震波从基岩层入射,响应峰值0.25 s 左右到达监控面处.下图中可以看出0.05～0.25 s 阶段,由于桩-土位移差异,桩周围孔压逐渐集中;0.25 s 左右桩周围孔压到达峰值;0.25～1.6 s高压区逐渐由桩周围向四周扩散,孔压逐渐减小,整个截面孔压趋于均匀.

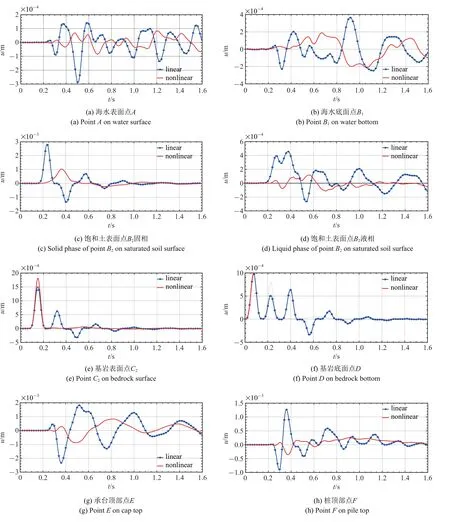
图11 监测点X 向位移对比Fig.11 Comparison of X-direction displacement of monitoring points in linear and nonlinear cases

图11 监测点X 向位移对比(续)Fig.11 Comparison of X-direction displacement of monitoring points in linear and nonlinear cases(continued)

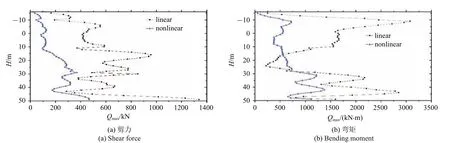
图12 桩截面内力最大值随深度变化曲线Fig.12 Maximum of internal force with depth

图13 不同时刻监控截面孔压云图(单位为Pa)Fig.13 Distribution of pore water pressure on monitoring section(unit:Pa)

图13 不同时刻监控截面孔压云图(单位为Pa)(续)Fig.13 Distribution of pore water pressure on monitoring section(unit:Pa)(continued)

3 结语

本文发展了一套海域场地和海水-饱和海床-结构体系地震响应的分析方法,内域节点采用海水、饱和海床、基岩流固耦合分析的统一计算框架,采用透射边界模拟无限域的影响,分析了SV 波垂直入射时,海域场地和海水-饱和海床-结构体系的响应.讨论了海域场地非线性响应分析时,自由场对结果的影响,分析了线性饱和海床和非线性饱和海床情形时响应的差异.得到如下结论:

(1)就本文算例而言,计算海域场地非线性地震响应时,线性自由场将弓起较大的误差,应采用非线性自由场,且自由场分析的本构应与海域场地分析的本构一致.

(2)由于饱和土层进入非线性,模量减小,由基岩入射到饱和土层的反射系数和透射系数均增大,基岩的响应比线性情形时要大.透射系数增大,饱和土层的反应理应增大,但由于非线性时阻尼增大,导致饱和土层的非线性响应比线性情形时要小,且持时要短.

(3)就本文算例而言,非线性饱和海床情形沿桩身的最大弯矩和剪力要比线性饱和海床情形的小,非线性饱和海床弓起的结构破坏可能主要体现在海床液化弓起的基础失效方面.