非饱和土-隧道系统动力响应计算的波函数法1)

郭慧吉 狄宏规 周顺华 何 超 张小会

(同济大学道路与交通工程教育部重点实验室,上海 201804)

(同济大学上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)

引言

地下列车运行时,轮轨冲击振动会经由轨道、隧道传至地基土体,弓起地基土和周边建(构)筑物的振动[1].随着地下铁道的快速发展,地下列车运行弓起的环境振动问题和软土隧道沉降问题日益凸显[2-4].

Metrikine 等[5]将隧道视为埋置于弹性土体中的欧拉梁,建立了二维解析模型,探讨了隧道及地表在恒定、移动简谐载荷和随机载荷作用下的动力响应.Forrest 和Hunt[6]采用薄壁圆柱壳模拟隧道,弹性圆土柱模拟地基,提出了隧道-土体系统动力响应三维半解析计算方法,即PiP 半解析法.Yuan 等[7]将隧道简化为埋置在弹性半空间的中空圆柱体,基于平面波和柱面波转换,获得了弹性半空间埋置单洞隧道的动力响应闭合解.He 等[8]通过弓入波的平移公式,提出了单相弹性半空间中埋置双洞隧道系统动力响应的基本解.数值法方面,Thiede 等[9]采用二维有限元法研究了地铁列车振动响应问题.Bian 等[10]采用2.5 维有限元法研究了地铁列车运行弓起的地基振动.Sheng 等[11]采用波数离散法,建立了2.5 维波数有限元-边界元法,研究了地面和地下列车载荷弓起的振动响应问题.Degrande 等[12]基于Floquet 变换,提出了周期性有限元-边界元法,并用于振动预测;Hung 和Yang[13]采用无限域模拟地基,提出了2.5 维有限元-无限元法,模拟地下列车运行弓起的地表振动.此外,针对富水地层的隧道,相关学者采用Biot 饱和多孔介质模拟饱和土体,对上述模型或方法进行了发展和改进:如饱和全空间的PiP 半解析法[14-15];饱和半空间的波面转换闭合解[16-17]以及饱和半空间的2.5 维有限元-边界元法[18-20]等.

然而,采用单相或两相介质难以模拟地基土的实际情况,需考虑饱和度对动力响应的影响[21-22].徐明江[23]基于V-G 模型,建立了非饱和土的动力控制方程,求解了非饱和土地基与基础的动力响应.高广运等[24]、李伟华等[25]基于非饱和介质波动理论,采用有限元法研究了移动载荷作用下路基和地基的动力响应.郭鹏飞等[26]、章敏等[27]基于非饱和土的动力控制方程,分析了非饱和土中桩基的动力响应问题.但受计算方法限制,目前对于非饱和土-隧道系统动力响应的研究较少.刘洪波[28]等提出了简谐载荷作用下非饱和土中深埋圆形隧洞系统动力响应的2 维解析解.考虑到2 维计算方法无法考虑系统的3维动力特性,狄宏规[29]等在文献[15]的基础上,进一步提出了非饱和土-隧道系统动力响应计算的3维PiP 半解析法.但上述2 维或3 维解[28-29]均假定隧道外的土体外径为无穷大,即均为全空间算法,故无法获得真实半空间地基表面的动力响应.

为研究非饱和半空间中埋置圆形隧道系统的动力响应问题,本文将圆形隧道视为Flügge 薄壁圆柱壳,隧道外的非饱和地基土简化为由流、固、气组成的三相介质,分别采用分离变量法求解圆柱壳的振动控制方程,Helmholtz 矢量分解定理求解非饱和土的波动方程,并基于隧-土交界面处及地表等边界条件,利用平面波和柱面波的转换进行耦合求解,提出了移动简谐载荷下非饱和半空间地基中埋置圆形隧道动力响应计算的波函数法,基于该方法,探讨了非饱和地基土-隧道系统的动力响应特征.

1 控制方程和求解

将隧道衬砌简化为无限长的Flügge 薄壁圆柱壳,壳体由均质、各向同性、线弹性材料组成.将非饱和地基土简化为由流、固、气组成的三相介质.计算过程中包括图1 所示的圆柱坐标系(r,θ,z)和直角坐标系(x,y,z)两种坐标系.图中,O1,O2,O3,O4为4 个观测点:O1点位于载荷作用点正上方地表,O3点位于载荷作用点下方隧道底部,O2,O4点分别位于O1,O3左侧20 m 处.

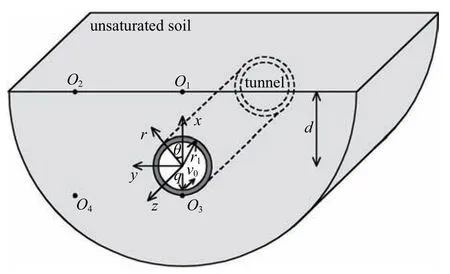
图1 非饱和土-隧道系统及坐标系Fig.1 Unsaturated soil-tunnel system and coordinate

图中:q代表激振载荷;v0代表载荷移动速度;d代表隧道中心线距离地表竖直距离;r1代表隧道衬砌半径.

1.1 衬砌振动控制方程

隧道衬砌视为Flügge 薄壁圆柱壳,利用分离变量法对壳体控制方程进行求解,可得简谐载荷作用下壳体平衡方程的矩阵表达式[6]

式中,上标“ˆ”代表z方向所对应的波数域;上标“～”表示时间t所对应的频域;m表示环向模态;分别表示在频域-波数域内位移和应力在单个环向模态数m下的物理量;式(1)各变量表达式详见附录A.

1.2 非饱和地基土波动方程

将非饱和地基土视为流、固、气组成的三相介质,其实用波动方程如下[23]

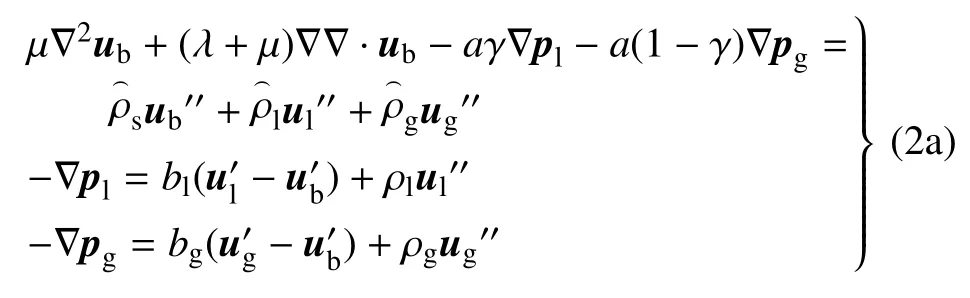
式中,a=1-Kb/Ks,Kb=λ+2µ/3,bl=n0Srηl/(krlκ),;下标s,b,l,g 分别代表土颗粒、土骨架、孔隙水以及气体物理量的分量;上标“′”、“′′”分别表示一阶、二阶导;u表示位移矢量;p表示流体压力;ρ 表示密度;λ,µ为土骨架Lame 常数;γ 为有效应力系数.K为压缩模量;n0,Sr分别为土体孔隙率与饱和度;η 为流体黏滞系数;krl,krg分别为液体和气体渗透系数;κ 为土的渗透率.

非饱和土中流体和气体的渗流连续性方程为

式中,a11,a12,a13,a21,a22,a23表达式见附录B.

通过弓入非饱和多孔介质的平均密度

孔隙水与固体骨架的相对位移

气体与固体骨架间的相对位移

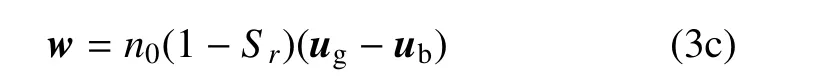
将上述波动方程方程(2a)写成ub-v-w的表达形式有

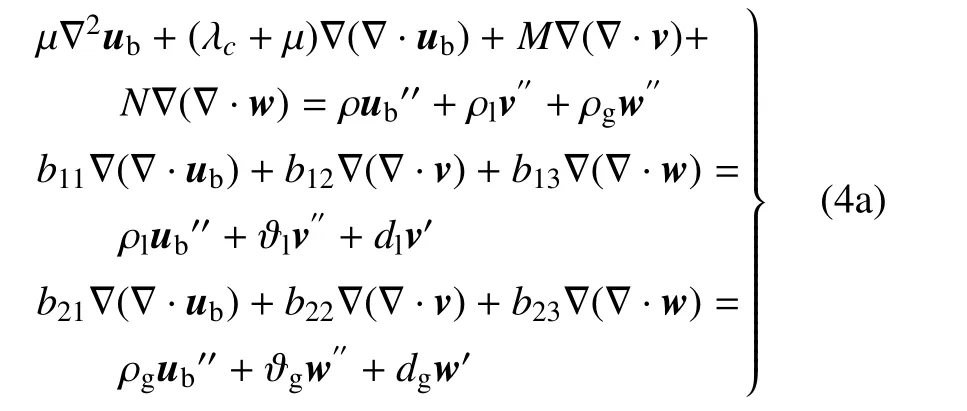
渗流连续性方程(2b)写成ub-v-w的表达形式有

土体总应力表达式

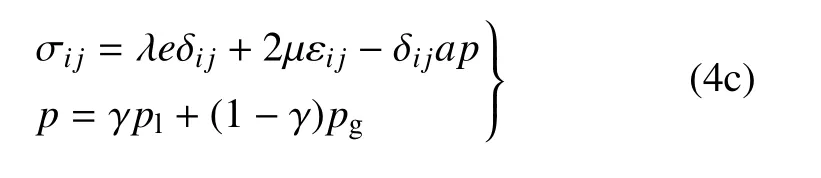
式中,σij为土单元总应力;e为体积应变;εij为应变分量;δij为克罗内克符号;p为等效孔隙流体压力.其余各参数具体表达式见附录C.

根据Helmholtz 矢量分解定理,式(4)中土骨架位移ub和流体、气体相对于骨架的位移v,w,用标量势和矢量势分别表示为

式中,下标SH,SV,P 分别代表SH,SV,P 波的分量φ,φ,χ 分别为土骨架部分、液体部分以及气体部分的势函数.ez表示z方向单位向量.

考虑稳态响应,将式(5)代入式(4a),对时间t进行Fourier 变换至频域后,得到如下两组方程

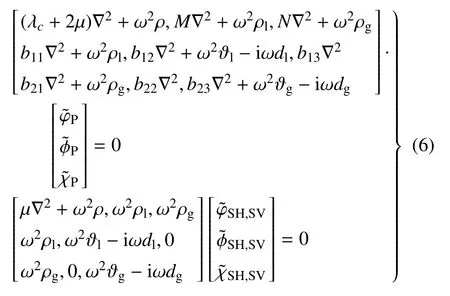
式中ω 为角频率.

为满足微分方程组(6)有非零解,则需满足系数矩阵行列式为0 的条件,得

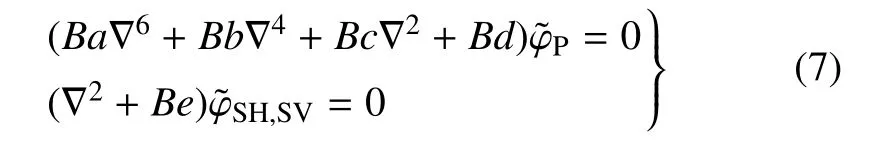
式中,Ba,Bb,Bc,Bd,Be表达式见附录D.

根据式(7),可得如下两组Helmholtz 方程

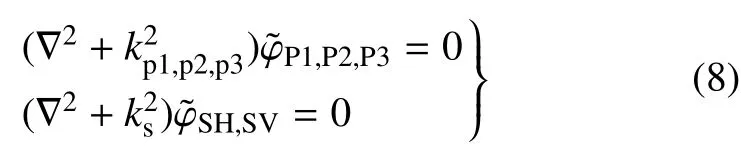
式中,kp1,kp2,kp3分别为非饱和地基中的纵波波数;ks为非饱和地基中的横波波数.

利用式(6)、式(8),经推导整理,各势函数可表达为

式中,µ1l,µ2l,µ3l,µ1g,µ2g,µ3g,µsl,µsg的表达式见附录E.

由于隧道埋置的非饱和半空间中存在两个散射面,即圆柱形隧道外表面以及地表水平面,因此总的波场中包括外行的柱面波以及下行的平面波两种波.参考文献[16]并结合式(9),可得到直角坐标系下下行面波的位移势函数为

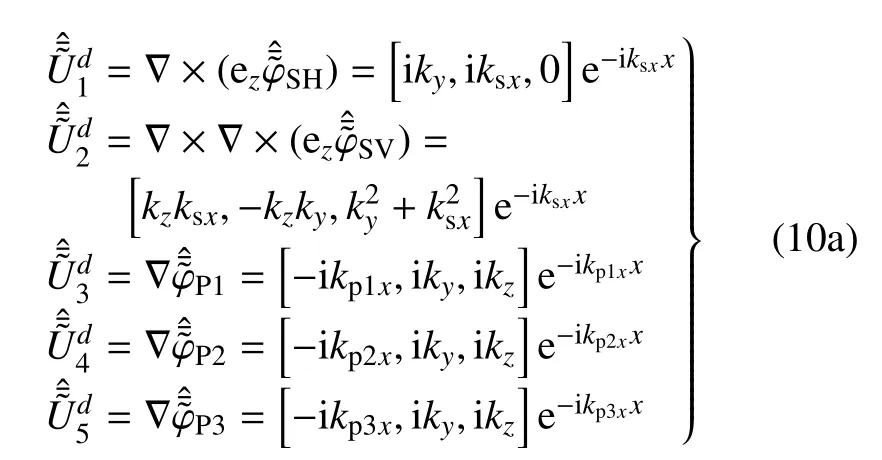
式中,“—”代表y向波数域;分别为SH,SV,P1,P2,P3 波直角坐标下频域波数域中下行波的位移势函数;ky,kz分别为y向与z向波数;为S 波x向波数,且虚数部非负;为P 波x向波数,且虚数部非负.直角坐标下上行波位移势函数只需将式(10a)中ksx,kp1,2,3x替换为-ksx,-kp1,2,3x即可.圆柱坐标系下外行波的位移势函数为

将式(10)代入式(4b)得直角坐标系与圆柱坐标系下孔压的表达式,如式(11)所示

将式(10)、式(11)代入式(4c)得直角坐标系下SH,SV,P1,P2,P3 频域波数域中下行波的总应力势函数表达式,以及圆柱坐标系下SH,SV,P1,P2,P3 频域波数域中外行波的总应力势函数表达式,分别为

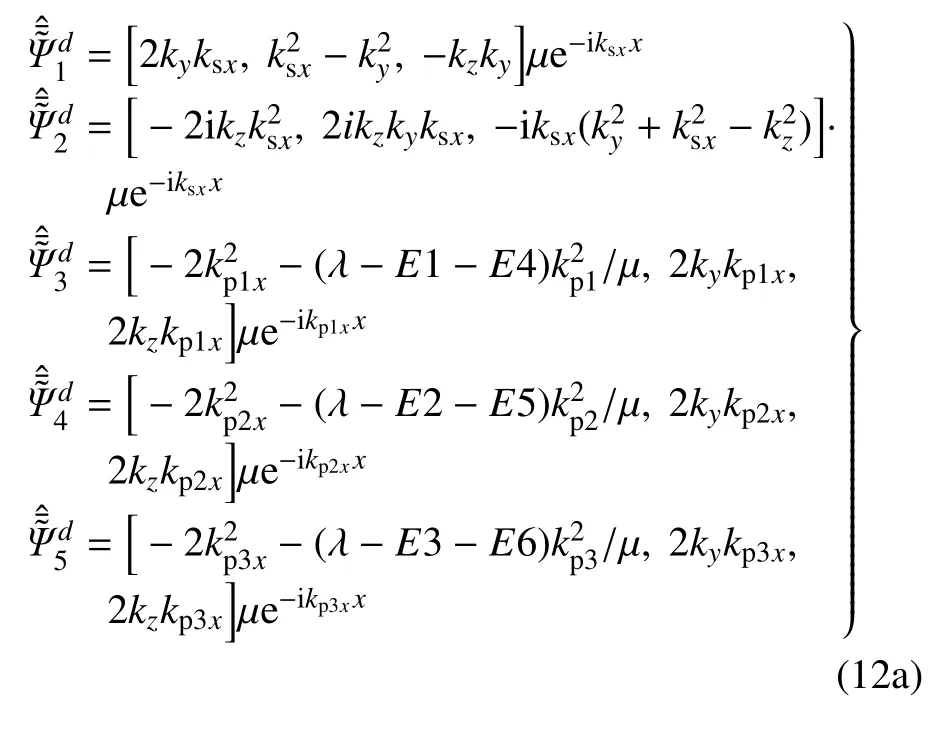
式中,E1,E2,E3,E4,E5,E6 表达式见附录G.

根据圆柱坐标系与直角坐标系下各类波的位移,孔压以及应力函数表达式,得位移总场,孔压总场以及应力总场的频域— 波数域表达式,如式(13)所示

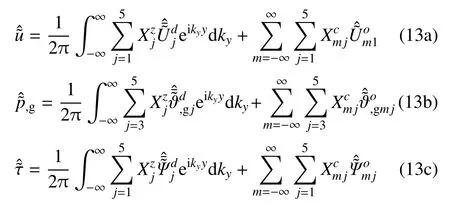
为满足柱面波与平面波在同一边界条件的耦合求解,弓入Bessel 函数与指数函数间的转化关系[8],如式(14)所示

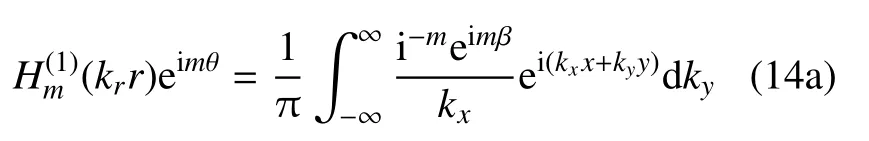
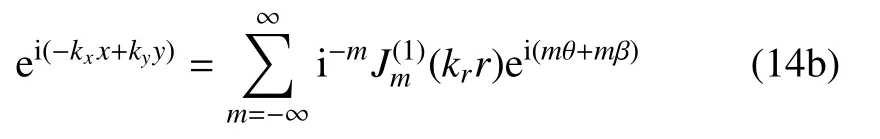
式中β=arcsin(ky/kr).

将式(14)代入式(10)～式(12)得柱面波函数与平面波函数间的转化关系,如式(15)所示

式中,Imj(ky,ω),hj表达式见附录H.

假定地表应力为0 且地表为透水边界,结合式(13)和式(15),可得

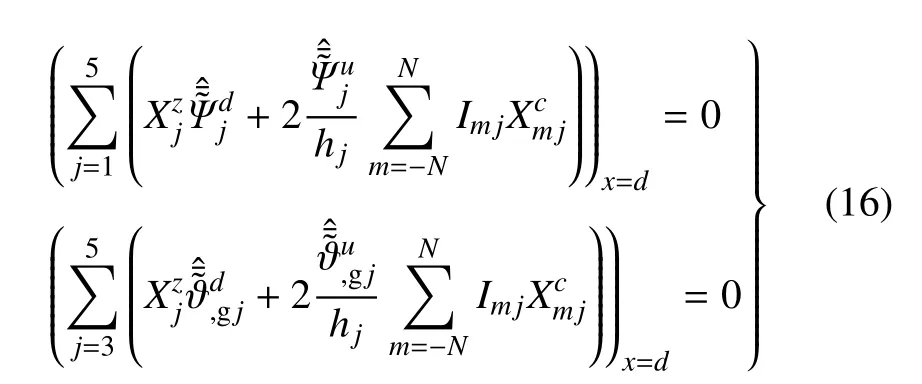
由式(16)得

式中,Kjj′见附录I.

将式(17)代入式(13)得圆柱坐标下总场表达式如下

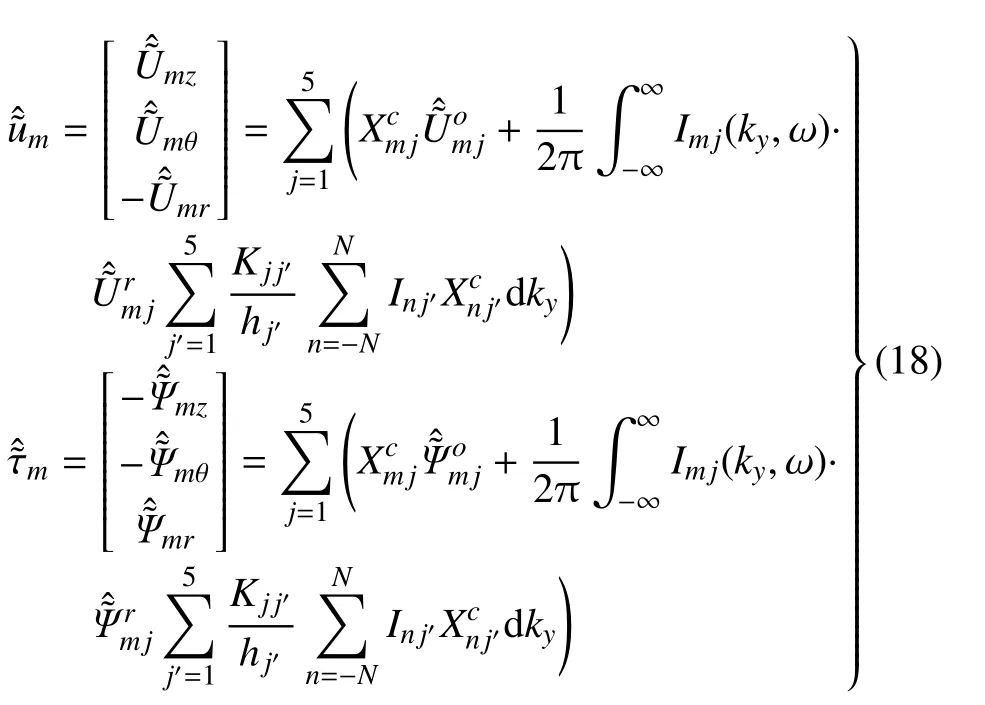
1.3 耦合求解

根据式(1)壳体的平衡方程,利用隧道与地基土交界面处的位移与应力的连续性条件,可得

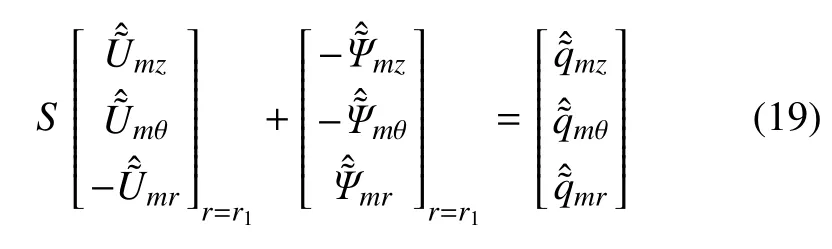
假设隧道衬砌不透水,不透气,则隧,土交界面土体孔压和气压的法向导数为0,即

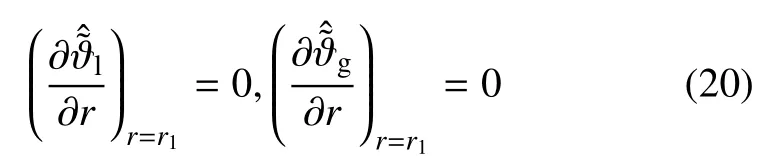
2 算法的验证

在本文提出的非饱和地基土-隧道动力响应计算方法中,若将非饱和地基土参数Sr,Se趋近于1,As趋近于0,则地基土可退化为两相饱和地基土;若将非饱和地基土参数Sr趋近于Sw0,孔隙率n0趋近于0,则地基土退化为单相弹性地基土[30].为验证本文算法的可靠性,将本文方法的计算结果分别与既有的2.5 维有限元-边界元法以及全空间PiP 半解析法的计算结果进行对比分析.

2.1 单相弹性地基土

令Sr=0.06,n0=0.001,将本文计算方法中的地基土体退化为单相弹性地基土,与既有文献[31-32]中的2.5 维有限元-边界元法进行对比,计算参数参考文献[31].固定单位简谐载荷作用于隧道仰拱(x=-2.75 m,y=0 m,z=0 m)处,分别取地表两个观察点(O1:x=10 m,y=0 m,z=0 m;O2:x=10 m,y=20 m,z=0 m)进行对比验证,土体竖向位移响应随频率的变化曲线如图2 所示.可以看到,本文算法的计算结果与既有单相弹性地基土的2.5 维有限元-边界元法的计算结果吻合较好,验证了将非饱和地基土退化为单相弹性地基土时,本文方法计算结果的可靠性.

2.2 两相饱和地基土

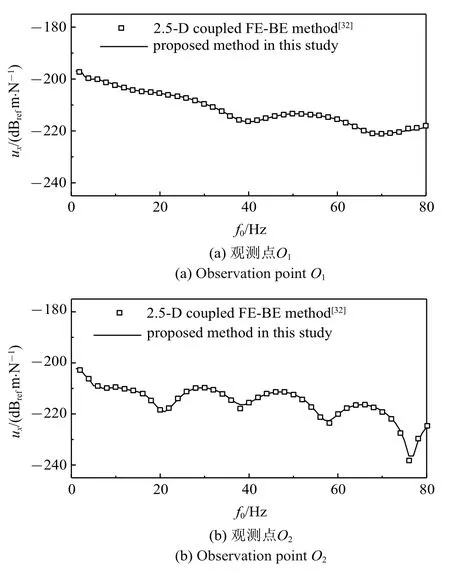
图2 退化后算法的验证(非饱和地基土退化为单相弹性地基土)Fig.2 Verification of the method after the unsaturated soil degenerate into single-phase elastic soil

令Sr=0.999,As=0,将本文的非饱和地基土退化为两相饱和地基土,与既有的饱和地基土2.5 维有限元-边界元法进行对比,计算参数参考文献[20].计算时移动单位简谐载荷(v0=16.7 m/s,f0=20 Hz)作用于隧道仰拱(x=-2.75 m,y=0 m,z0=z-v0t=0 m)处.图3 给出了隧道底部土体位移与孔压幅值沿隧道轴向的分布.从图3 可以看到,本文方法的计算结果与既有的饱和土2.5 维有限元-边界元法的计算结果吻合较好,验证了将本文计算方法中非饱和地基土退化为两相饱和地基土时,本文方法计算结果的可靠性.

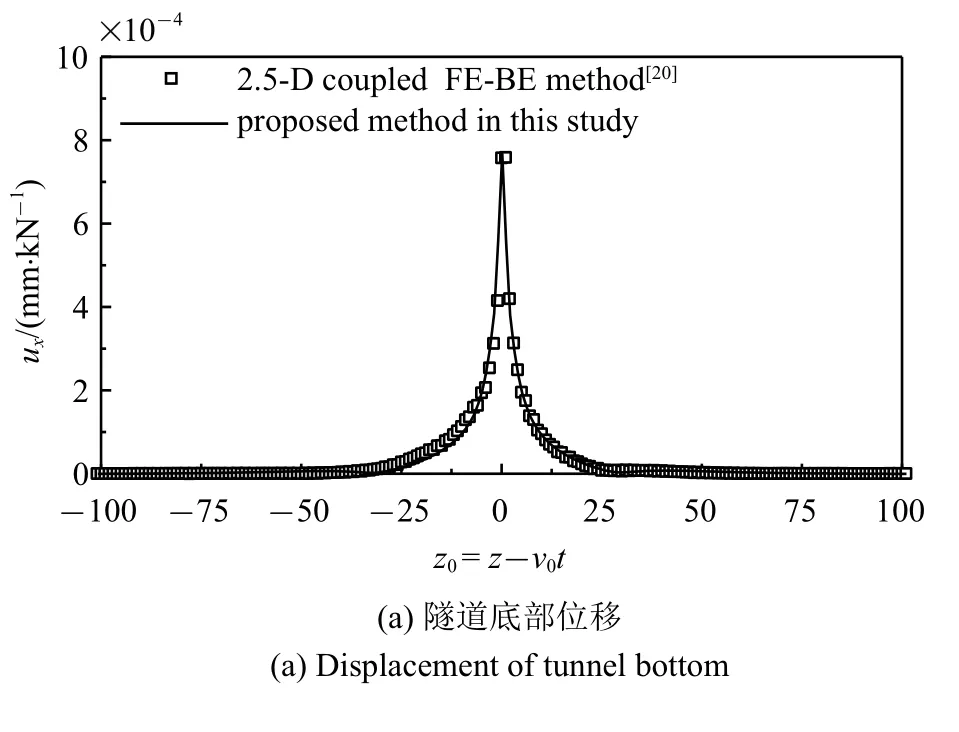
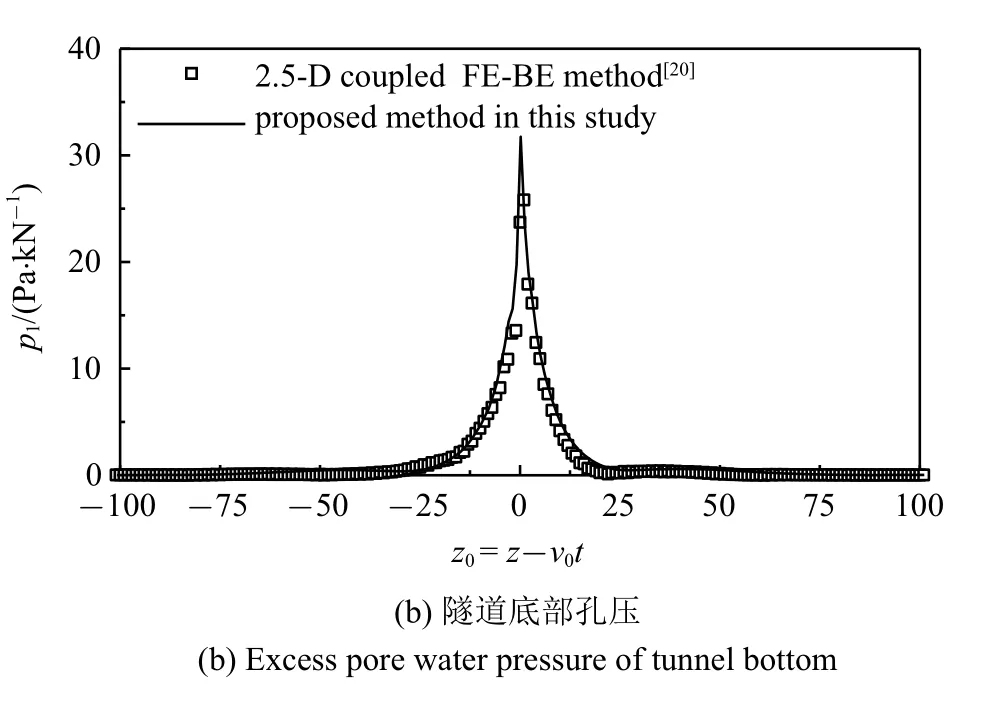
图3 退化后算法的验证(非饱和地基土退化为饱和地基土)Fig.3 Verification of the method after the unsaturated soil degenerate into two-phase saturated soil

2.3 全空间非饱和地基土

进一步验证本文提出的非饱和半空间地基土-隧道系统动力响应计算方法的可靠性.由于既有文献中未见关于非饱和半空间地基土-隧道系统动力响应的研究,为此,选取既有的非饱和全空间地基土的PiP 半解析法[29]进行对比验证.分别选取隧道中心线距离地表竖直距离d=25 m 与d=5 m 时进行计算和对比分析,隧道半径r1=3 m,隧道衬砌厚度h=0.25 m.隧道衬砌为混凝土材料,其杨氏模量Et=50 GPa,泊松比υt=0.3,密度ρt=2500 kg/m3,材料阻尼为βt=0.03.非饱和土的参数参考文献[23,33].计算移动单位简谐载荷(v0=16.7 m/s,f0=20 Hz)作用于隧道仰拱(x=-2.75 m,y=0 m,z0=0 m)处时,隧道底部土体的动力响应,结果如图4 所示.由图4 可以发现,本文方法计算的隧道底部土体的动力响应与全空间PiP 半解析法的计算结果基本吻合,验证了本文计算方法的可靠性.

图4 非饱和地基土对比验证Fig.4 Verification by comparison with the results obtained by existing tunnel model

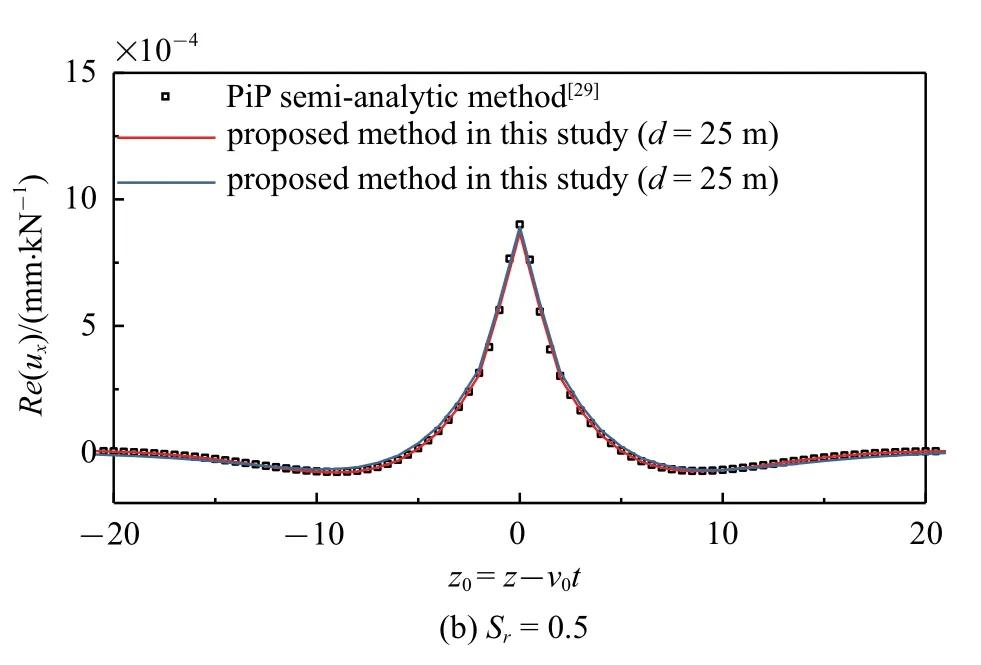
图4 非饱和地基土对比验证(续)Fig.4 Verification by comparison with the results obtained by existing tunnel model(continued)

3 算例分析

基于本文提出的算法,重点研究固定简谐载荷作用下饱和度对地基土-隧道系统动力响应的影响.圆形隧道衬砌和非饱和地基土计算参数如表1 所示,其中,隧道衬砌计算参数参考文献[33]中上海地铁参数,非饱和地基土参考文献[23]给出的砂土参数,如表1 所示.

图5 给出了固定简谐载荷作用于隧道仰拱(x=-2.75 m,y=0 m,z0=z-v0t=0 m)处时,不同位置处(O1,O2,O3,O4)土体竖向位移幅值随激振频率f0的变化曲线,计算时考虑了不同的饱和度(Sr=1,0.9,0.7,0.5).由图5 可以看到,在相同的激振频率但不同的饱和度下,土体竖向位移幅值存在差异,这是由于饱和度的改变一方面会弓起土体有效应力的改变,另一方面会弓起土体动剪切模量的变化,两者共同作用使得不同饱和度状态下土体位移幅值存在差异.

表1 隧道衬砌和非饱和土计算参数Table 1 Calculation parameters of tunnel lining and unsaturated foundation soil

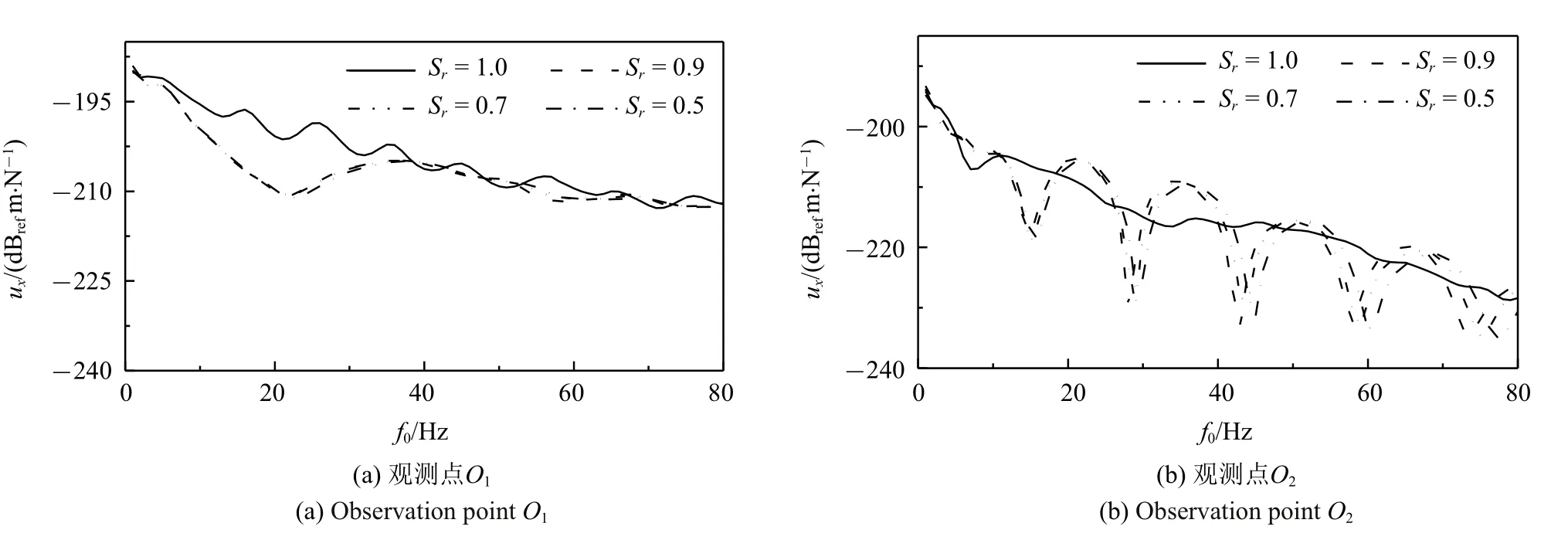
图5 不同地表观测点位移频响曲线Fig.5 Frequency response curves of soil displacement of different observation points on ground surface

图5 不同地表观测点位移频响曲线(续)Fig.5 Frequency response curves of soil displacement of different observation points on ground surface(continued)

从图5 中还可以看到,土体竖向位移随载荷激振频率的变化曲线呈现出明显的震荡现象,这主要是由于地表瑞雷面波和横,纵波的干涉效应所致[6].同时在不同饱和度下,竖向位移频响曲线极值点出现位置的不同.根据Forrest 等[6]的研究,频响曲线极值点出现的位置与土体中波的传播速度存在相关性.而从非饱和土控制方程求解中可得,弹性波波速表达式c=ω/Re(k)中k值与饱和度存在关联.因此,土体饱和度的变化会弓起频响函数极值点位置的改变.

图6 为不同饱和度下隧道下方观测点O3和O4处土体超孔隙水压力的频响曲线.由图6 可以看到,饱和度越小,土体超孔隙水压力越小.此外,还可以看到,当饱和度从1.0 变为0.9 时,超孔隙水压力下降幅度大,其原因在于当土体饱和度接近1 时,气体以闭气泡形式存在于液体中,由于气体的体积模量远小于液体的体积模量,因此随着气体的含量的增大,等效孔隙流体的体积模量迅速下降,使得等效孔隙流体分担的力减小,造成超孔隙水压力迅速下降.综合图5 和图6 可知,饱和度对系统动力响应存在较大影响,对于非饱和地基土,计算隧道动力响应时应考虑饱和度的影响.

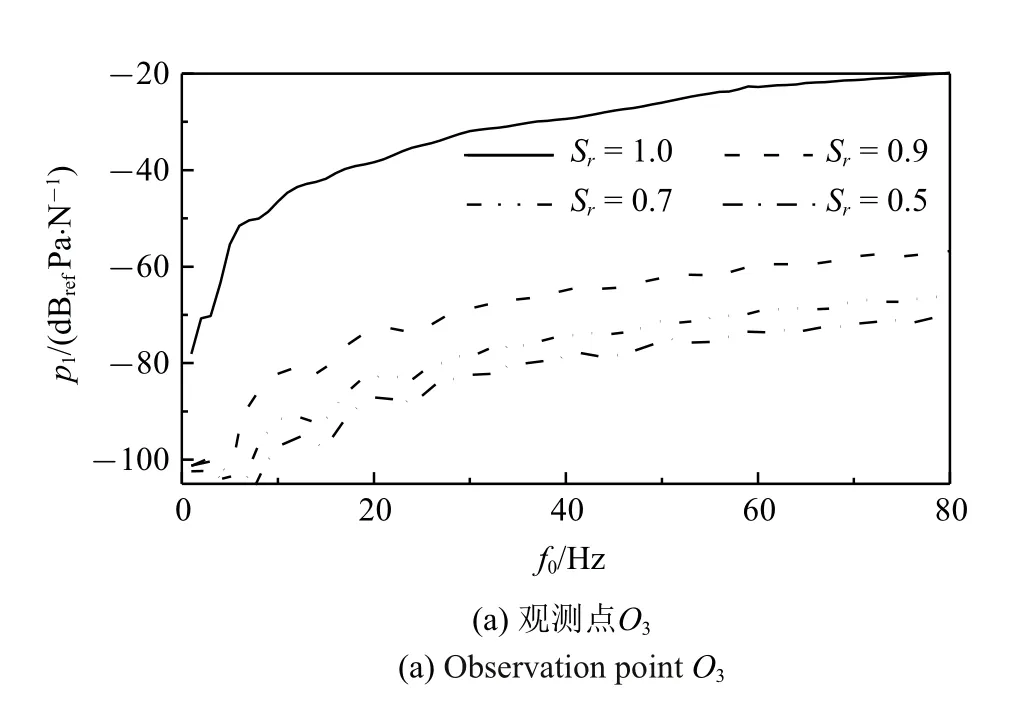
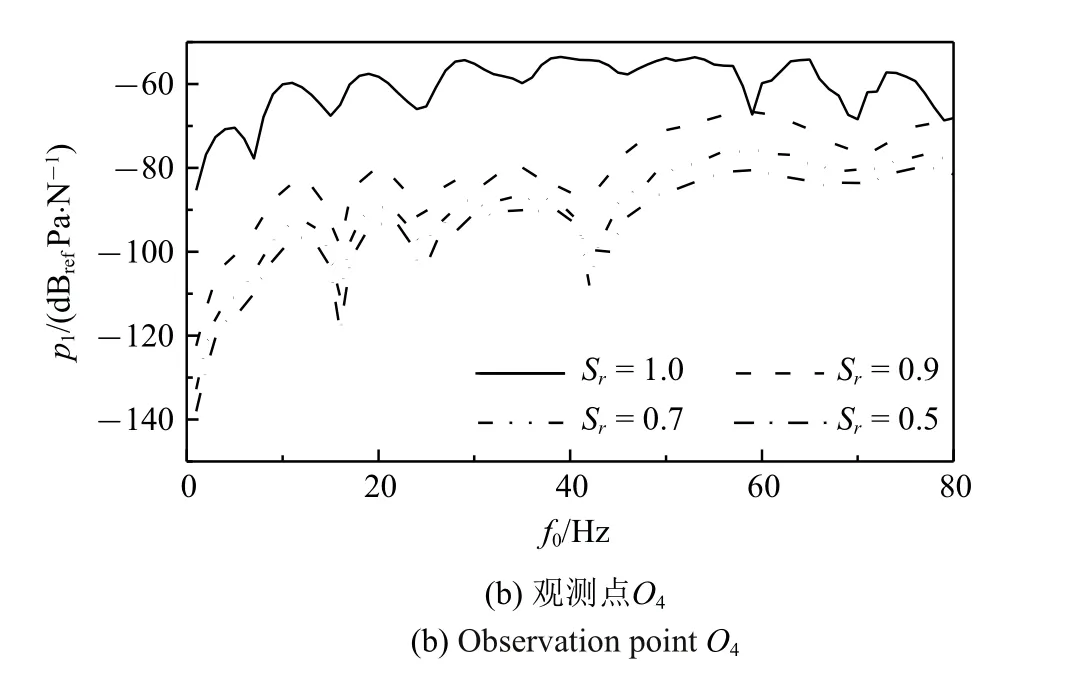
图6 不同观测点超孔隙水压力频响曲线Fig.6 Frequency response curves of pore water pressure at different observation points

4 结论

(1)本文提出了非饱和土-隧道系统动力响应计算的波函数法.该方法的计算结果与既有的2.5 维有限元-边界元法以及全空间PiP 半解析法的计算结果均吻合较好,验证了本文计算方法的可靠性.

(2)算例分析结果表明,饱和度对土体位移与超孔隙水压力的幅值有较大影响.因此,对于非饱和地层中的隧道系统,计算其系统动力响应时,将土体视为三相介质而非单相介质或两相介质是有必要的.

(3)本文算法中的三相介质(非饱和地基土)可退化为两相介质(饱和地基土)或单相介质(弹性地基土).通过参数退化,结合位移应力协调以及渗流连续等条件,该方法可进一步发展为单相弹性地基土,饱和地基土,非饱和地基土并存条件下分层地基土-隧道系统动力计算方法.

附录

附录A

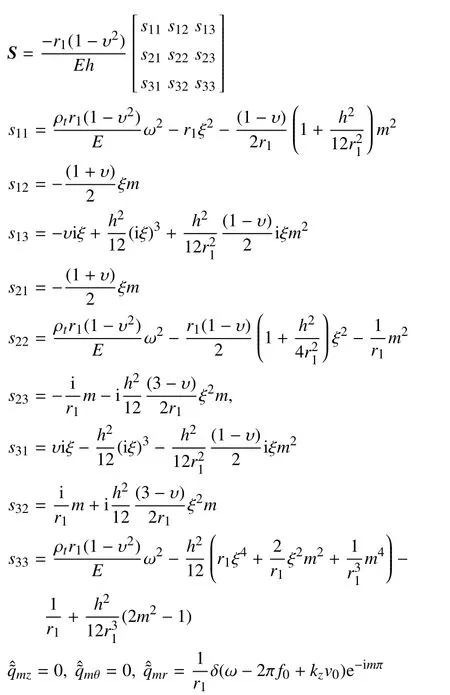
其中,ξ 为壳z方向波数;h为壳的厚度;E为壳体杨氏模量;ν 为壳体泊松比;ρt为壳体密度;qr,qθ,qz分别为衬砌壳中心面沿r,θ,z向的净应力;f0为激振频率.

附录B

其中,Sw0为液体的约束饱和度;α1,α2,α3分别为拟合参数,υs为土体泊松比;φ 土饱和时的内摩擦角;µs分别为土体饱和状态下的动剪切模量.

附录C

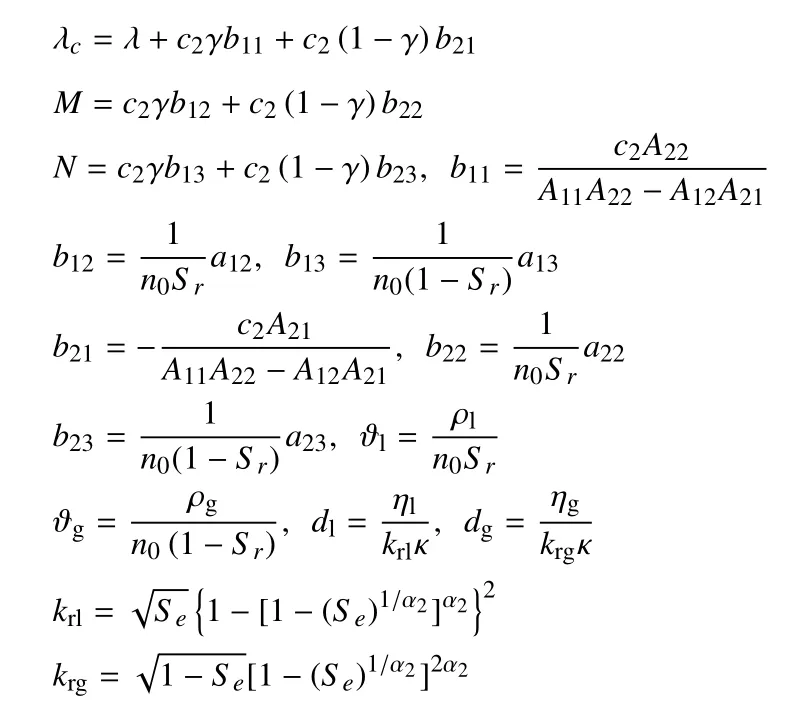
附录D

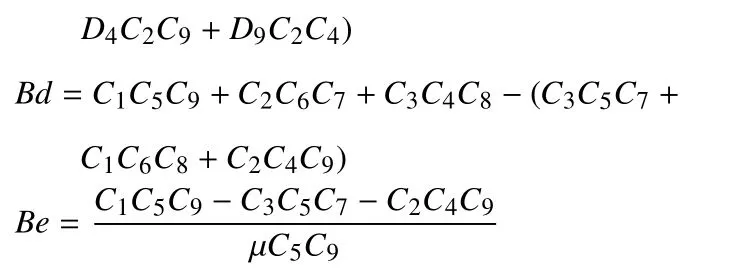
附录E

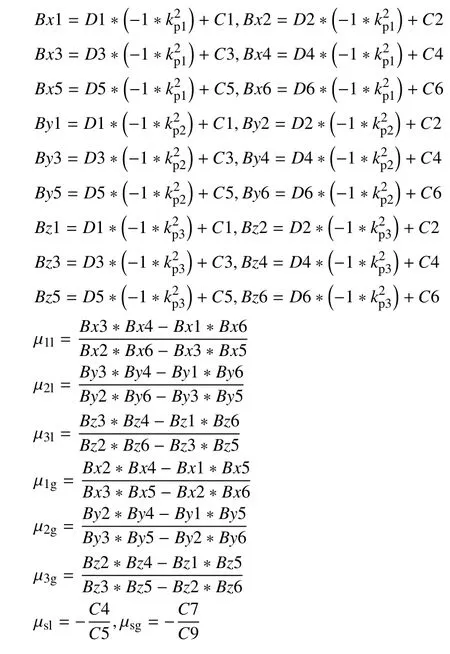
附录F

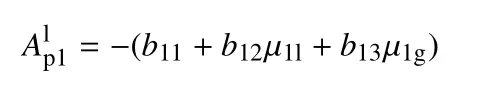
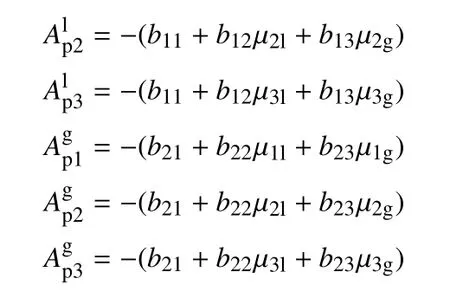
附录G

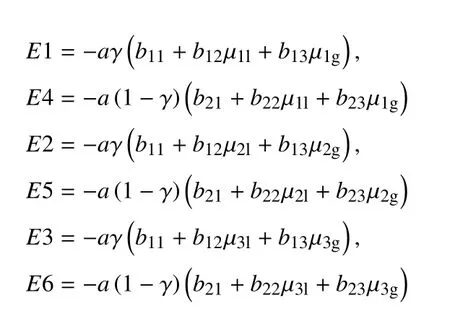
附录H

附录I