基于原子体积场拉普拉斯算子对金属玻璃剪切转变区的预测1)

史荣豪 肖 攀 杨 荣

*(中国科学院力学研究所,北京 100190)

†(中国科学院大学工程科学学院,北京 100049)

引言

金属玻璃作为一种特殊非晶材料,有着很多优异力学性能[1],大多是高温液体快冷形成,其内部还保留类似液体的结构,但是原子已经被冻结,没有原子团的大尺度运动[2].快速冻结的同时也在原子尺度上造成金属玻璃的不均匀性,有原子相对密集的区域,也有原子相对稀疏的区域,密度和模量近似于高斯分布[3].这种不均匀性是金属玻璃的本质特征[4],也是导致金属玻璃拥有独特塑性变形行为的重要原因[5].晶体金属的基本缺陷形式是位错[6],它具有明显的几何特征.然而,由于金属玻璃中原子排列的无序特性,导致其缺陷的识别存在争议和困难.

为解释非晶的塑性变形机制,在硬球模型[7]基础上,Spaepen[8]提出自由体积模型,认为在外力作用下非晶的塑性变形的过程是原子不断跳到附近的空隙中,因此自由体积越多的地方就类似于非晶的缺陷.该模型应用在很多宏观分析中简单有效,但自由体积模型确定的缺陷却往往在后续加载中没有失稳,因此将其作为非晶微观塑性变形的核心机制仍存在争议[9].Argon[10]进一步提出剪切转变区(shear transformation zone,STZ)模型,认为非晶的塑性变形是局部原子团的剪切变形.Schall 等[11]在胶体玻璃实验中观测到原子团的剪切变形,证实了STZ 事件.外界持续的加载会激发很多STZ 事件,STZ 的相互渗透最终形成剪切带导致宏观的失稳断裂[12].研究表明,类似于Eshelby 夹杂,STZ 呈现出四极非仿射位移场(quadrupolar nonaffine displacement field)特征[13].但要识别出金属玻璃中哪些区域容易激发STZ事件,在理论上仍不完善,在实验上更加困难[2].

近年来计算机技术的发展使分子动力学模拟方法广泛应用于金属玻璃研究[14-20].分子动力学可以追踪每个原子的运动,清晰地展示金属玻璃内部的原子结构,再结合数学上的Voronoi 多面体,可以得到局部五次对称性.宏观上,Li 等[19]研究了五次对称性和金属玻璃弛豫时间的关系,Zhang 等[20]发现一个局部五次对称性的阈值,超过该阈值金属玻璃就会展现出局域的塑性变形.微观上,Tian 等[16]进一步利用五次对称性定性研究应变梯度和剪切带的关系,发现高应变梯度有助于形成剪切带,但实际上应变梯度是源自于金属玻璃本身的非均匀性,并且五次对称性无法解释STZ 的形成机理,因为仅靠构型无法描述原子运动的规律,还需要考虑原子间的相互作用.

原子间相互作用在计算机模拟中是用势函数来计算的.如果将金属玻璃的原子视作简谐振子,可以用势函数计算整个体系的动力学矩阵,对角化动力学矩阵的模态分析可以得到整个体系的声子谱[21].大量模拟计算表明金属玻璃低频模态偏离德拜模型,形成玻色峰[22-24].这些低频模态为主的原子在体系中是准局域分布的,具有相对低的激活能,更容易塑性变形,通常被称为“软模”[25-27],与塑性变形密切相关.宏观上,Yang 等[23]采用Voronoi 多面体法寻找出玻色峰的方向序,将玻色峰的方向序和金属玻璃模量相关联.微观上,Ding 等[27]结合Voronoi 多面体法找到了软模的结构特征,发现软模主要是一些几何不利构型(geometrically unfavored motifs,GUMs),这些构型被视为缺陷.软模在小应变下和STZ 事件发生区域对应度较好,但是当应变很大,比如接近剪切带形成时,一个STZ 事件可能涉及过多模态,软模的效果无法达到像位错一样的准确[28].Ding 等又进一步提出可动体积(flexible volume),在与初始STZ事件强相关的基础上,可动体积还和剪切模量线性相关,但仍然缺乏定量的相关性分析[29-30].梯度算子也是很有用的[31-33],Xu 等[34]用应力梯度以及ARTn (actication-relaxation technique nouveau)等计算方法,较准确地定量预测了加载应变小于5%的STZ事件及其顺序,但应变大于5%的STZ 事件甚至剪切带未涉及,并且ARTn 需要多次求解全局动力学矩阵,计算时间复杂度太高.另一方面,通过原子的刚度[35]或者动力学矩阵[13]可以直接计算出原子的非仿射位移,但是STZ 的四极非仿射位移场是如何形成的却不清晰,其背后的力学机理仍需作进一步地分析.

本文对金属玻璃初始构型的原子体积场(V)进行局域平均得到平均原子体积场,采用其梯度和拉普拉斯作为金属玻璃体系非均匀的表征,低的区域为局部软区,描述软区体积梯度场的局域分布.基于和构造参数ξ,通过阐明ξ、非仿射位移和STZ 三者的关联,来预测金属玻璃中STZ 形成位置.

1 计算模型和方法

本文针对经典的Cu64Zr36金属玻璃体系,采用分子模拟方法展开机理研究.为考虑不同尺寸对结果的影响,分别计算了3 种不同尺寸体系,它们的尺寸如表1 所示.其中样本1 含有9000 个原子,x,y,z三方向长分别为Lx=6.0 nm,Ly=12.0 nm,Lz=2.0 nm,3个方向都采用周期性边界条件,模型如图1 所示.体系的z方向尺寸较小,以便于对模拟结果进行准二维的结构分析.模拟中采用EAM 势来描述原子之间的相互作用[36].分子动力学模拟采用LAMMPS 开源软件包[37],原子构型结果采用Ovito 进行可视化[38].

3 种金属玻璃样本均采用相同方法制备.首先生成Cu64Zr36面心立方晶体,将该晶体在零压下加热到2500 K 并弛豫2 ns 得到稳定的高温熔融液体.然后以1013K/s 的降温速率将体系急冷至1 K 并弛豫100 ps得到稳定的金属玻璃,最后通过共轭梯度法进行能量极小化得到0 K 下Cu64Zr36的金属玻璃结构.图2是所生成样品体系的径向分布函数(radial distribution function,RDF),具有明显的玻璃态特征.进而对样品进行非热准静态剪切加载(athermal quasi-static shear,AQS shear),每一个加载步都对整个体系在x方向上施加应变为0.01%的简单剪切[13],然后对体系进行能量极小化,得到当前加载步的平衡状态用于构型和结果分析.

表1 3 种尺寸参数对照表Table 1 Parameters of three sizes

图1 样品1 的构型和尺寸Fig.1 The configuration and dimensions of sample 1

图2 金属玻璃体系的径向分布函数Fig.2 RDF of the prepared metallic glass sample

2 结果和讨论

2.1 局部原子应变响应

图3 是样品1 在剪切加载下的应力应变曲线,应力最大值出现在应变为9.0%附近(图中红色虚线标注的点).在应变小于9.0%时,应力已经出现了多个明显的不连续跳动,这说明体系内有局部屈服事件的发生.由于金属玻璃变形行为的特殊性,不同文献所定义的屈服点位置有所不同[2-3,36],在本文中,定义屈服阶段为应力值最大点(在这里应变为9.0%)之后的阶段.

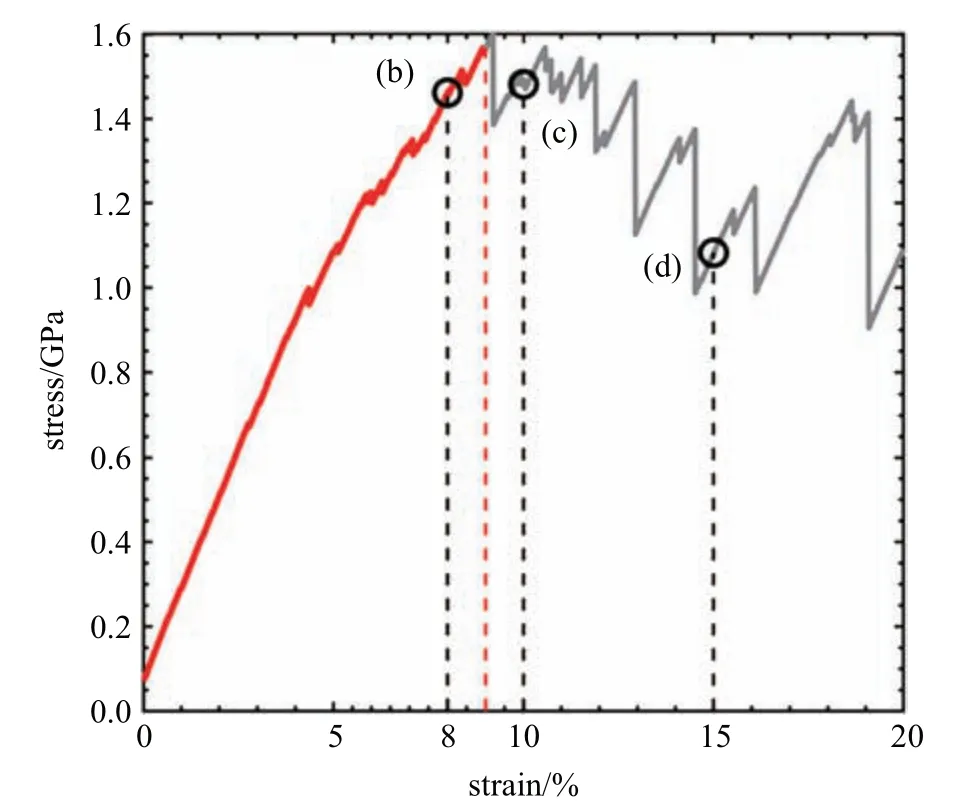
图3 样品1 的应力应变曲线Fig.3 Stress strain curve of sample 1

局域原子团的剪切变形被称为是STZ 事件[10],并且局域剪切变形的发生让瞬间的宏观模量和应力产生奇异性[13],导致应力和能量的不可恢复性跌落[40],是金属玻璃在外力作用下塑性流动的载体[41].在微观上寻找经历了剪切变形的STZ 原子需要对比变形前后局域原子构型的相对变化[42].为研究体系局部变形行为,本文采用Mises 原子应变[43]来刻画每个原子的邻域变形特性,其中,第i个原子的Mises原子应变记为.图4 给出了体系在剪切应变分别为8.0%,10.0%和15.0%时分布图.从分布图可以看出,与图3 的结果相对应,体系从应变为9.0%时进入屈服阶段,在应变为15.0%时,可以明显看见剪切带.

图4 应变为8.0%,10.0%和15.0%时的原子应变分布图Fig.4 The distribution of atomic strain when γ=8.0%,10.0%and 15.0%

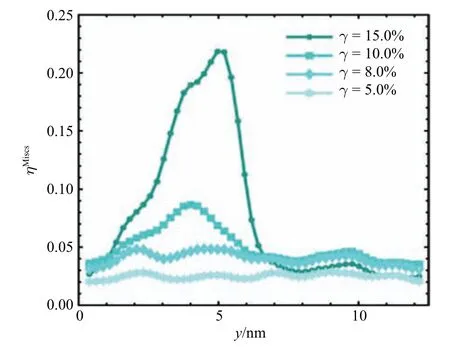
图5 平均原子应变在y 方向分布图Fig.5 The distribution of averaged atomic strain along y axis

图5 曲线分别给出了体系在不同剪切应变下,y方向上平均原子应变随着剪切加载的演化过程.从图4 和图5 结果可见,体系进入屈服阶段后,在y=4.0 nm 附近,出现了一个明显的峰值,表明体系在该区间的应变较大,最后剪切带形成的位置在y=2.0 nm 到y=6.0 nm 之间.值得注意的是,在屈服之前剪切应变为8.0%时,在y=5.0 nm 附近已经出现了相对的峰值.为了找出STZ 原子,本文设定一个应变间隔Δγ=0.1% 和阈值.如果存在γ ∈[0.1%,9.0%],使得原子i的原子应变改变量满足

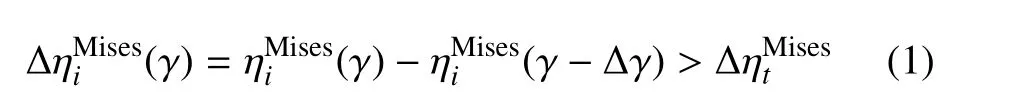
则该原子在应变为γ 时经历了STZ 事件,将该原子记为STZ 原子.图3 中第一个STZ 事件具有最低的ΔηMises=0.005,因此取0.005 可以选出所有的STZ 原子.同一个样品重复加载,其应力应变曲线、STZ 事件和剪切带的位置是相同的[44].因此,STZ 事件以及剪切带和金属玻璃的初始结构有密切关系.为建立金属玻璃初始构型与STZ 形成之间的关联,需要对体系初始构型的非均匀性进行表征.

2.2 局域非均匀性表征

原子体积及其相关参数,如原子数密度、自由体积,可以作为金属玻璃局部非均匀性的直接反映.在分子模拟中,原子体积一般采用Voronoi 多面体法进行计算[29],即原子i与其近邻各原子间的垂直平分面所包围的多面体的最小体积视为原子体积Vi.对每个原子作体积云图(图6 左)并不能直接反映体系的局部非均匀性,而需要以原子为中心,取一定的特征尺寸,对其进行空间平均,才能有效反映局部体积的分布.Wei 等[45]研究了各种有预测STZ 能力的参数,发现它们空间自相关函数的特征尺度都和STZ 平均尺度差不多.STZ 原子团的平均尺寸为1～1.5 nm[46],因此本文以原子i为球心,取平均半径rave为1.0 nm 进行空间平均,得到的原子体积的平均值记为.

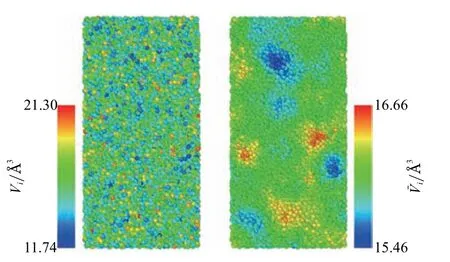
图6 初始构型Vi (左)和 (右)的分布Fig.6 The distribution of Vi (left)and (right)in initial configuration

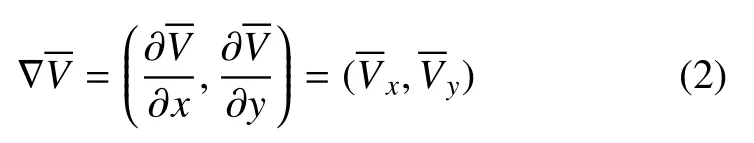
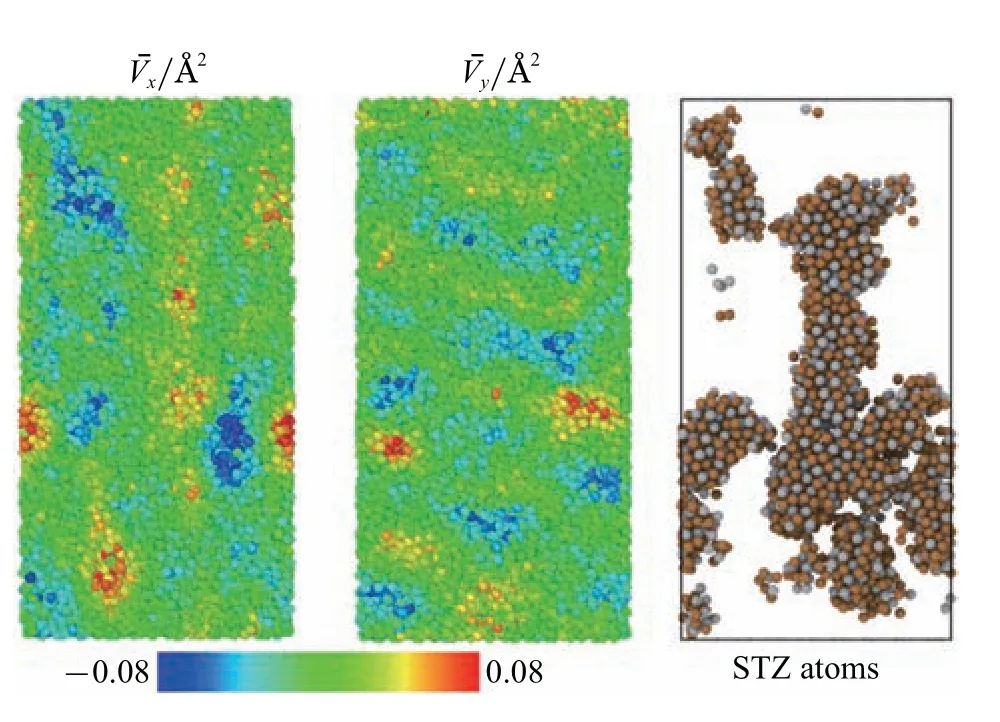
图7 初始构型(左)和 (中)的分布以及由式(1)确定的STZ原子分布(右)Fig.7 The distribution of(left),(middle)in initial configuration and STZ atoms determined by Eq.(1)(right)

2.3 原子体积梯度与非仿射位移场的统计关系

对于连续均匀的弹性体系,在剪切作用下,其内部的位移场为仿射位移场r°.大量计算表明[13,47],由于金属玻璃的非均匀性,内部原子的实际位移场r在仿射位移场r°的基础上存在非仿射位移场部分r*,即r=r°+r*.系统剪切应变为γ 时的非仿射位移场为

其中Δr°=(Δγ·y,0),为仿射位移增量.研究表明,在STZ 事件发生的应变间隔内,产生STZ 处的原子非仿射位移大,且呈四极漩涡状[48],这一非仿射位移特征反应出其附近的剪切应变得到加强,从而出现剪切局部化.

非仿射位移的产生是由于系统原子经过仿射位移后受力并不平衡,还有残余的仿射力场Ξ.单个原子的与r*的关系如下[13]

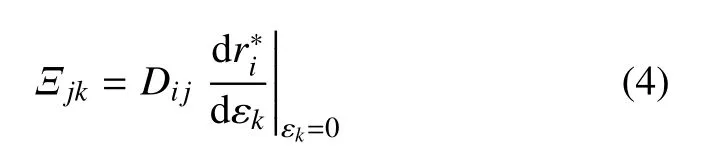
其中Di j为该原子的局部动力学矩阵.由式(4)可知,金属玻璃中原子非仿射位移场的大小和方向与体系内部原子排列的非均匀性特征以及外部载荷的加载方向和大小相关.为了简化分析,这里考察二维金属玻璃中一个原子的非仿射位移与其周围非均匀刚度的关系.设方向1 和方向2 为该原子的两个主应变方向.k1+,k1-,k2+和k2-分别表示该原子由于周围局部不均匀性或者对称破缺而感受到的刚度.由于主应变方向当i≠j时Di j=0,所以此时该原子的局部动力学矩阵只有两个非零元素Dj=kj++kj-.假设该金属玻璃在方向j产生应变εj,该原子由于自身附近刚度的不均匀在应变εj的基础上产生非仿射位移.在一阶近似下由式(4)可得该原子的非仿射位移为

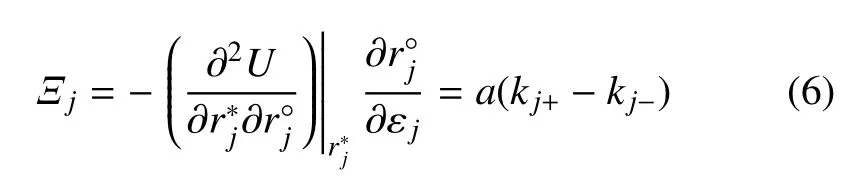
其中a为原子间的间距,U为原子的势能.由此可以算出该原子的非仿射位移r*为

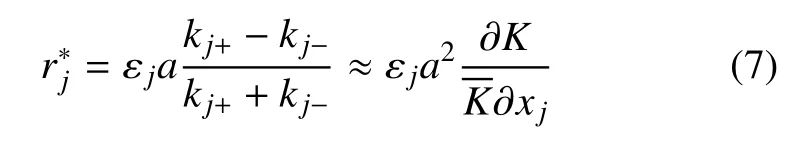
图8 非仿射位移与非均匀原子体积的关系Fig.8 The relationship between nonaffine displacement and the heterogenous atomic volume

其中j=1,2 表示不同主方向.当ε1=γ0并且ε2=-γ0时,r*与∇K沿轴1 对称.在金属玻璃体系中,原子所受的非均匀刚度场是由于周围邻近原子的不均匀分布而产生的.从势函数的特性可知,在平衡态附近,当邻近原子靠得越近,其所受等效刚度也会越大.因此,原子周围的刚度场梯度与原子体积梯度是负相关的.由式(7)可得,r*与∇V沿轴2 对称,即可以近似认为在纯剪切下如图8 所示,原子的非仿射位移方向与原子体积梯度方向沿y=-x轴对称.为了验证这一近似,对样品中原子的非仿射位移与原子体积梯度的方向进行了统计,如图9 所示.图9 中统计了剪切带形成前的所有弹性阶段非仿射位移向量与体积梯度沿y=-x对称后的向量之间夹角的分布.夹角在0 附近最多,表明这个对称关系在统计上成立.不同曲线是按梯度向量模长为阈值选取,当梯度向量模长越大时,夹角在0 附近越多.即原子体积梯度值越大,它与非仿射位移的方向对称性越好.

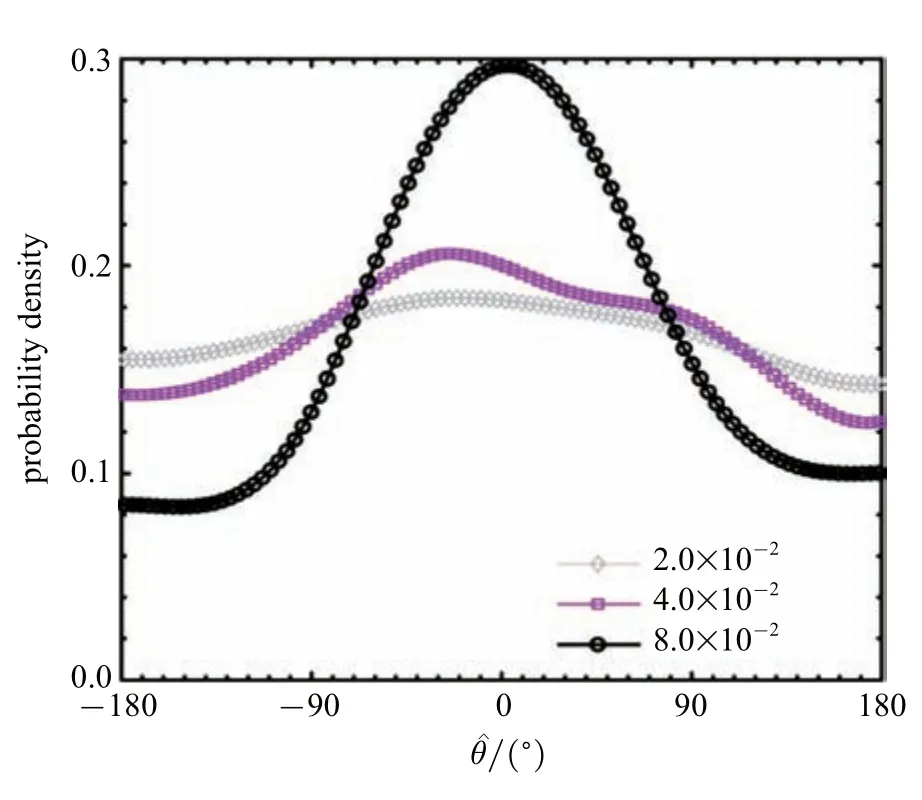
图9 与r* 的夹角分布Fig.9 Distribution of angles betweenand r*

2.4 原子体积梯度分布特征与剪切局部化

对非晶材料的原子非仿射位移场的计算研究表明[13],产生STZ 处的原子非仿射位移大,其方向呈四极漩涡状,表明局部剪切变形得到加强.从上一节的分析可以看出,如果非仿射位移呈四极漩涡状,则相应的原子体积梯度分布如图10(a)所示.从这一结果可以看出,要使得原子非仿射位移场呈现出一种使得局部剪切变形能得到加强的模式,的分布也要呈现出特定的形式,而不仅仅是原子体积梯度的模量越大即可,这也是为什么原子体积梯度与STZ 形成的区域没有直接的相关性.进一步的分析可以看出,图10(a)的软区呈现出向内指的特征,而这正是原子体积梯度场散度的特性,即当在该区域的散度为负时,原子非仿射位移场呈现出局部剪切变形加强的模式.为此,可以定义的散度即原子体积的拉普拉斯算子,来表征的分布特征.从物理上来看,为正表示该处的体积梯度向量有向外发散的特征,而体积梯度向量指向原子体积增大的方向,表明越往中心位置,原子体积越小,即该区域更硬,反之则更软.相比梯度要求原子体积的变化出现局部化,而不仅仅是在某一方向上有变化.

图10 与r* 的对应关系.(a)软区的场与四极非仿射位移的对称关系,(b)仅x 方向上梯度大,(c)仅y 方向上梯度大,(d)仅y= x方向上梯度大,(e)仅y=-x 方向上梯度大Fig.10 The relationship between and r*.(a)Symmetry betweenof soft region and quadrupolar nonaffine displacement.(b)Large gradient only in the x direction.(c)Large gradient only in the y direction.(d)Large gradient only in the y= x direction.(e)Large gradient only in the y=-x direction

2.5 基于原子体积拉普拉斯算子对STZ 的预测

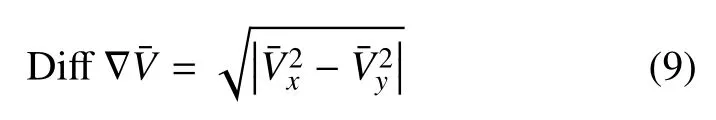
式中Ωave为初始结构下所有原子的平均体积,作为分母使ξ 无量纲化.基于参数ξ,对样品的初始构型进行分析,来预测STZ 出现的位置.图11(a)是ξ 的云图,颜色越红的区域就相对周围越软,云图上的点为所有STZ 原子的分布,可见STZ 原子与红色区域在空间上有较高的重合度.图11(b)为云图内选取的两个局部放大图,图中红色箭头就是体积梯度场,很明显图11(b)A 与B 分别对应图10(b)与图10(c)的软区梯度场.

为了验证采用参数ξ 作为金属玻璃缺陷识别的可靠性,对参数ξ 和STZ 区域的相关性展开了分析.为此,先确定两个阈值:ξt和.其中在式(1)中用来选出STZ 原子,集合Sγ包含在应变间隔为[γ-Δγ,γ]时出现的所有STZ 原子,集合S包含在应变间隔(0,γ]内出现的所有STZ 原子,显然

图11 ξ 云图,STZ 原子与 的分布图Fig.11 The contour plot of ξ,the spatial distribution of STZ atoms and

记体系原子总数为N,集合S的原子数为NS.ξt用来找出软区原子.记集合P包含所有ξ 值大于ξt的原子作为可能会经历STZ 事件的软区原子集,集合P的原子数为NP.根据ξ 的云图本文选择ξt=2.0×10-5.Sγ∩P是集合Sγ的子集,包含距离集合P小于3.5 Å(图2 中RDF 曲线的第一个极小值点,仅包含了近邻的原子)的STZ 原子,即为应变间隔[γ-Δγ,γ]内预测成功的STZ 原子集.图12 的柱状图是NSγ∩P/NSγ,即每一个应变间隔内的预测准确率.柱状图中有些应变间隔没有数据是因为该间隔内没有STZ 事件.将所有的条形值平均得到平均的预测率为76.3%.图12的红色曲线是采用的Manning 等[26]使用在软模上的相关性算法

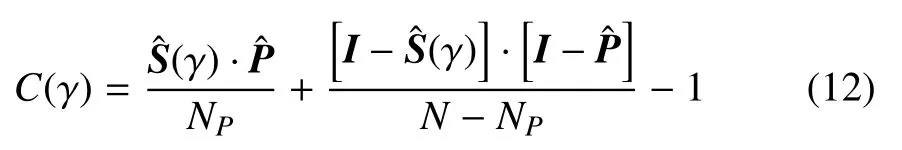
图12 每一步的准确率(柱状图)与累计相关性(红色曲线)Fig.12 Accuracy in each step(bar plot)and cumulative correlation index(red solid curve)

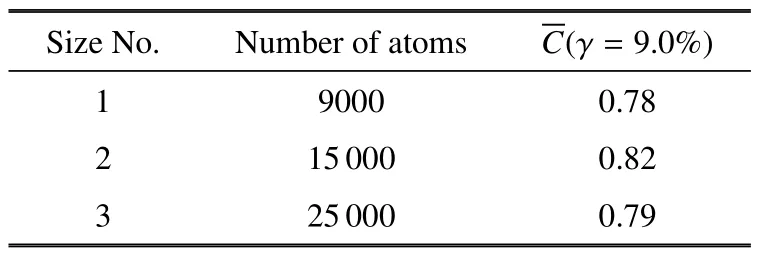
表2 3 种尺寸的平均C(γ=9.0%)Table 2 Averaged C(γ=9.0%)of three sizes

值得说明的是,参数ξ 的计算是基于金属玻璃体系的初始构型,随着剪切加载的进行,STZ 等塑性事件不断出现,在STZ 附近的原子构型也将发生变化,导致局部的受力状态和原子体积场的分布与初始构型发生偏离.因此,虽然图11(a)中对于样品应变从0.1%到9.0%之间的STZ 原子,具有较好的预测性,但其中仍有部分参数ξ 比较大的区域并未与STZ 区域重叠.实际上,如果把统计应变放宽到10.0%,会发现该区域正好处在剪切带边缘,有大量STZ 原子覆盖,如图4.因此,如果想要得到更加准确的预测结果,需要考虑计算每个STZ 事件对局域构型的影响,并更新参数ξ.另一方面,图11 中参数ξ 云图是基于原子体积平均场得到的(平均半径为1 nm),它是对局部区域的表征,而STZ 原子是直接由单个原子的应变参数选择出来的.因此,STZ 原子与参数ξ 云图并非一一对应.正如STZ 事件本身描述是原子团的变形行为,而非只针对某一原子.

虽然本文仅将参数ξ 用在0 K 下进行金属玻璃的缺陷识别,但是ξ 仍然可以用在有限温度下.在给定温度和加载方式下,与均与温度无关,ξ 只是初始构型的函数,同样可以用来寻找初始构型中的局部软区,不过此时还需要在一定时间尺度上进行平均才能得到构型的平衡态.

3 总结

本文采用非热分子模拟方法对三种不同尺寸的Cu64Zr36金属玻璃在受剪切加载时的局域塑性变形行为和STZ 事件的结构起源展开了准二维的机理研究和简单的理论推导.在没有随机热振动的干扰下,体系的初始构型和外界的加载形式是STZ 产生的决定性因素,因此可以通过分析金属玻璃初始结构来预测在特定加载形式下STZ 事件的可能位置.虽然原子体积场及其梯度可以用来表征金属玻璃中局部原子构型的非均匀性,但它们与STZ 的真实产生区域没有明显对应关系.由于STZ 原子有很明显的局部剪切增强性非仿射位移场,所以本文基于非仿射位移理论,在二维情况下进一步推导,发现在纯剪切下原子体积的梯度向量与原子的非仿射位移有对称关系,并且通过本文分子模拟中的统计结果加以证实.基于此,本文提出一个新的局域结构参数ξ 来预测金属玻璃中STZ 事件可能的产生区域,ξ 是两个因子的乘积:原子体积场的拉普拉斯算子和体积场梯度分量的绝对差(Diff).初始构型中较大的区域,向量的箭头向内汇聚,表示原子体积向内逐渐变大,代表体系中的局域软区;而Diff则用于在五种向量分布模式中筛选出指定的三种分布模式.本文发现Diff值比较大的局部软区,其特定的向量分布模式在对称关系下将导致形成局部剪切增强的非仿射位移场,从而更容易诱发局部STZ 事件,由此建立了ξ、非仿射位移和剪切局部化三者关系.本文进一步采用两种不同的相关性算法对ξ 进行空间相关性分析,在3 种不同体系下该参数与STZ 原子分布区域的平均相关系数均高于78%.因此,在统计意义上,该参数能对金属玻璃在剪切加载下的局域STZ 事件进行有效的空间预测;在理论上,该参数中的拉普拉斯算子可以进一步深化STZ 结构起源的理论背景,并有望应用于金属玻璃力学行为的理论分析.