张紧式锚泊系统松弛-张紧过程冲击张力分析

乔东生， 漆徐良， 闫俊， 梁海志，2， 索云飞， 宁德志， 欧进萍

(1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2. 青岛理工大学 土木工程学院，山东 青岛 266033；3. 中交第四航务工程勘察设计院有限公司，广东 广州 510230)

深海工程中张紧式锚泊系统凭借诸多优于悬链式锚泊系统的特性而得到广泛应用。锚泊系统在随浮体运动过程中可能会出现松弛-张紧的往复变化，当浮体运动达到特定的频率与幅值时，会引起锚泊线内动张力接近或达到零张力，同时动张力最大值达到预张力的3倍甚至更高，即产生冲击张力。此现象可能导致锚泊线发生断裂，并严重影响锚泊系统的使用寿命，因此对锚泊线冲击张力的研究十分必要。

国内外学者对锚泊线冲击张力问题进行了相关研究，Huang等[1]基于集中质量-弹簧模型对锚泊线进行建模，用数值法预测锚泊线在松弛-张紧条件下缆绳内的冲击载荷，并利用实验所得数据对比分析，验证了该数值法预测冲击载荷的准确性。Plaut等[2]研究了刚性锚泊圆柱体的非线性动力响应，建立了锚泊线只受拉无质量弹簧模型，利用了解析法计算该模型的运动响应，研究发现在锚泊线发生松弛-张紧变换时会产生冲击张力，此时锚泊线内张力幅值明显增大，会对系统产生破坏。Vassalos等[3]对锚泊线进行了模型实验，结果表明动张力幅值会随激励幅值和频率的增加非线性增大，且一旦进入松弛-张紧变换状态，动张力幅值被显著放大，动张力频率出现高频成份。Lu等[4]研究了水下浮式隧道的锚泊线在波浪作用下产生松弛并发生冲击张力的现象，对影响结果的多项影响因素进行了考察，发现锚泊线随波高增大时，逐渐由张紧状态进入松弛-张紧变化状态，锚泊线内产生冲击张力。Palm等[5]提出了一种hp自适应非连续伽辽金法，该算法可以用来模拟锚泊线内的张力，通过不断调节该算法中的网格尺寸h以及多项式阶数p的大小，可以高精度地捕捉锚泊线内产生的冲击张力。唐友刚等[6]考虑深水锚泊线的拉伸和弯曲变形，用有限元方法对聚酯缆的力学性能进行了模拟，并研究了锚泊线的动张力变化规律。张素侠等[7-9]对锚泊线松弛-张紧变化过程中冲击张力的研究进行了一系列的实验，考察了冲击张力产生的影响因素。姜钧喆等[10]对深水半潜式平台与张紧式锚泊系统进行了时域的耦合动力分析，并考察了聚酯缆绳动刚度及锚泊线布置方式对平台的影响。张火明等[11]对张紧式锚泊线冲击张力的特性进行了研究，采用集中质量法对锚泊线建模，并通过Aqwa分析了锚泊线的运动响应，考察了预张力、顶端激励等因素对冲击张力的影响。

本文主要针对张紧式锚泊系统锚泊线在松弛-张紧变换情况下的冲击张力问题进行研究。采用数值模拟的方法，通过ANSYS有限元分析软件，对锚泊线进行建模，在顶端施加正弦位移激励模拟其运动过程，提取锚泊线松弛-张紧运动时激励端张力曲线，并做频谱分析，研究冲击张力的频谱特性及产生冲击张力的临界激励幅值与激励频率关系。

1 锚泊线建模及工况设置

1.1 锚泊线模型

本文基于ANSYS有限元分析软件对张紧式锚泊系统其中一根锚泊线进行建模。锚泊线采用Link180单元，单元几何模型如图1所示。锚泊线在运动过程中仅承受拉力，单元的拉压开关设置为仅受拉并且打开大变形开关，可以很好地模拟锚泊线运动响应。该原理是当判断单元内轴向应力为0或小于0时，则使该单元失活死亡，并且该死亡的单元并不会影响其余任意单元；当该单元轴应力判断大于0时，则就会重新激活该单元。本文采用有限元非线性时域分析的方法对系泊线松弛-张紧过程进行模拟，该方法在分析过程中采用牛孙拉夫逊法进行迭代求解动平衡方程，并且在每个时间步上都要重复采集新的系统质量矩阵、阻尼矩阵和刚度矩阵，因此该方法能很好的处理系泊线运动引起的强非线性问题。

图1 Link180单元几何模型Fig.1 Link180 geometry model

本文根据文献[12]选取了三段式链-缆-链张紧式锚泊线，总长1 610 m，锚泊线上端和下端各有一段80 m长钢链L1和L2，以及中间段1 450 m长聚酯缆绳L3，锚泊线为45°安装角度(锚泊线与水平面夹角)，跨度1 138 m，工作水深1 138 m。如图2所示，建立锚泊线的有限元模型和X-O-Z坐标系，将锚泊线底端节点与锚固点铰接约束，顶端节点在沿轴线方向预张力FPre作用下张拉到位于水平面的坐标系原点O，运动过程中顶端施加沿着X轴的正弦位移激励。

图2 锚泊线有限元模型Fig.2 FEM of the mooring line

锚泊线除受自身重力与浮力外，还受水动力荷载以及预张力。Ocean Load选项可以模拟锚泊线受到的水动力荷载，拖曳力系数Cd取1.2，附加质量系数Cm取1.0，本文模拟锚泊线在静水中的运动响应，不考虑波浪力和水流力。预张力可以通过弹性拉伸锚泊线施加所需的张力值。采用钢链-聚酯缆-钢链三段式锚泊线布置，其材料参数及水深、水动力参数等见表1。

表1 模型参数Table 1 Parameters of the Model

1.2 工况设置

采用锚泊定位的浮体，由于二阶波浪力的作用，需考虑其中的差频及合频成分，使得浮体在极端环境作用时，可能出现大幅和高频的运动，即为锚泊线的顶端激励。设置锚泊线的预张力Fpre=3×106N，顶端正弦位移激励振幅Am取值范围为0.5～5.0 m，并以0.5 m间隔增加，共设置10组不同幅值的激励；激励频率f取值范围为0.1～2.0 Hz，并以0.1 Hz间隔增加，共设置20组不同频率的激励。

2 计算结果与分析

2.1 动张力曲线及频谱分析

受篇幅所限，本文选取锚泊线聚酯缆绳段顶端单元动张力在一组位移激励振幅下随频率增大的变化趋势进行如下展示，其他组结果与本组变化趋势相近。

振幅Am=1.0 m，频率f依次取0.1、0.3、0.6、0.8和1.0 Hz，各频率下取平稳段10个周期数值进行处理，锚泊线激励端单元动张力在各频率下的曲线及频谱，如图3所示。

图3 锚泊线激励端单元动张力曲线及对应频谱图(0.1≤f≤1.0 Hz)Fig.3 Time histories of dynamic tension and spectra at the top end of mooring line (0.1≤f≤1.0 Hz)

从图3(a)可以看出，在低频激励下，锚泊线处于张紧状态，动张力曲线呈正弦形状，最大和最小动张力相对预张力对称，此时动张力频率为受迫振动的激励频率。从图3(b)～(d)可以看出，随着激励频率的增大，锚泊线仍处于张紧状态，但动张力曲线呈现出不同频率正弦曲线的叠加形态，从频谱图可以看出动张力频率除激励频率成分外，还产生了倍频成分。从图3(e)可以看出，随着激励频率继续增大，此时锚泊线已经由张紧状态进入了松弛-张紧变化状态，锚泊线动张力的最小值已经达到0张力，而此时动张力的最大值可达预张力的20倍左右，锚泊线的动张力响应时程显得混乱无章，频谱图也出现了多成分的高频成分，没有明显的卓越频率，表明整根锚泊线与激励的频率发生了共振响应。

通过比较动张力的最大值，可以看出，随着激励频率增大，动张力最大值非线性的上升，而锚泊线一旦进入松弛-张紧状态，动张力最大值会显著提升。为了研究动张力最大值是否会随激励频率增大而继续增大，本文继续比较了更高激励频率下动张力的变化趋势。

预张力与激励幅值保持不变，激励频率分别取1.2、1.4、1.6、1.8、2.0 Hz进行了计算，数值模拟结果，如图4所示。

图4 锚泊线激励端单元动张力曲线及对应频谱图(1.2≤f≤2.0 Hz)Fig.4 Time histories of dynamic tension and spectra at the top end of mooring line (1.2≤f≤2.0 Hz)

由图4可见，随着激励频率继续增大，锚泊线由松弛-张紧状态再次转入张紧状态，随后又进入松弛-张紧状态，而锚泊线动张力最大值随激励频率的继续增大呈现先下降后上升的趋势，动张力频率成分包含激励频率、倍频成分以及高频成分。

综合图3和图4中动张力随激励频率的变化规律可知，动张力的最大值并不是随激励频率增加一直呈上升趋势，而是呈现出先上升，再下降，后又升高的波动变化过程，且在锚泊线初次进入松弛-张紧变换状态时，动张力最大值显著增大。在激励频率增加的过程中，锚泊线运动也是由张紧到松弛-张紧再到张紧状态的交替转换。由于锚泊线存在多阶自振频率，随着激励频率的增加，每当激励频率与锚泊线的第i阶自振频率相一致时，则会引起松弛-张紧状态变换，发生共振响应，从而引起动张力的显著增加；而当激励频率与锚泊线的第i阶自振频率不一致时，锚泊线则处于张紧状态，此时未发生共振响应，则不会引起动张力的显著增加。

2.2 最大、最小动张力

预张力保持Fpre=3×106N不变，在激励幅值Am和激励频率f所有组合求解中，取锚泊线运动进入稳态的10个周期动张力进行比较。在不同激励幅值下，动张力的最大、最小值随频率变化趋势如图5所示。

由图5可见，一旦动张力最小值到达0时，锚泊线就会进入松弛-张紧状态，此时动张力幅值显著增大，即锚泊线内产生了冲击张力。

在多组不同激励幅值下，动张力的最大值随频率逐渐增大呈波动增大的趋势；当张紧式锚泊线初次进入松弛-张紧状态时，动张力显著增大，即图5第1个波峰处产生了冲击张力。当激励幅值较大时(如本例中Am≥2.5 m时)，动张力最小值在一定频率后全部达到0张力，说明张紧式锚泊系统的锚泊线发生了松弛，进入松弛-张紧状态；当激励幅值较小时，随着激励频率的增大，锚泊线经历了从张紧到松弛-张紧再到张紧状态的变化，从图5中也可以预见当激励频率继续增大，小幅值激励也将使锚泊线进入松弛-张紧状态。

从图5中还可以看到，激励幅值越大，锚泊线进入松弛-张紧的临界激励频率越小，且相同激励频率下，激励幅值越大，动张力最大值越大。

图5 动张力最大、最小值在不同激励幅值下随激励频率变化曲线Fig.5 Maximum and minimum dynamic tension versus excitation amplitude and frequency

2.3 临界激励幅值与频率

以上结果显示，锚泊线内动张力对激励幅值与激励频率变化非常敏感，当锚泊线顶端激励幅值与频率达到一定程度，张紧式系泊系统的锚泊线将进入松弛-张紧状态，而此状态下锚泊线内将产生数倍于预张力的冲击张力。图6展示了冲击张力产生的临界激励幅值与频率关系。

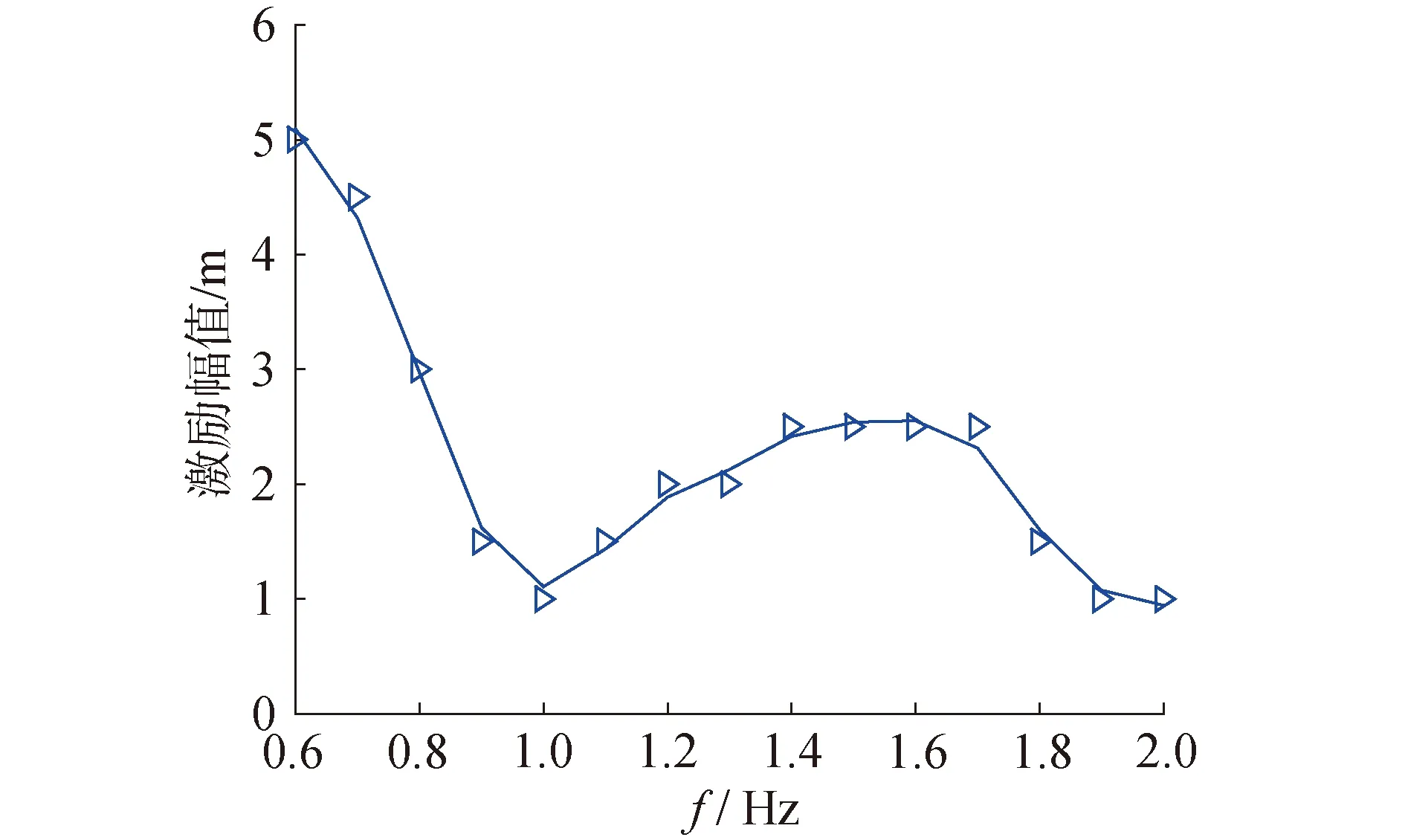
图6 产生冲击张力的临界激励幅值与频率Fig.6 The critical amplitude and frequency of snap load

在图6中，曲线展示了产生冲击张力的临界激励幅值与频率，曲线上部是冲击张力区域，即该区域为锚泊线松弛-张紧区域；曲线下部是未发生冲击张力的区域，即该区域内锚泊线为张紧状态。当激励频率保持不变，随着激励幅值的增大，锚泊线将由张紧状态越过临界曲线进入松弛-张紧状态；当激励幅值保持不变，随着激励频率的增加，锚泊线首先将经历张紧和松弛-张紧状态的交替变换状态，最后进入松弛-张紧状态。锚泊线处于临界曲线上的激励幅值与频率组合时，锚泊线内将会形成生冲击张力。

3 结论

1) 随着激励频率不断增大，锚泊线状态由张紧转向松弛-张紧，随后可能再次进入张紧状态，最终完全进入松弛-张紧状态。

2) 随着激励频率不断增大，动张力频率会形成高频，动张力最大值呈波动上升趋势；动张力最小值会在锚泊线进入松弛-张紧状态时达到0张力。

3) 锚泊线由张紧初次进入松弛-张紧状态时会产生冲击张力，通常冲击张力可达到预张力的20倍甚至更高。

4) 冲击张力临界曲线第1个下拐点及左侧曲线是发生冲击张力的最小临界条件，该曲线对系泊系统设计具有重要参考意义。

本文针对张紧式锚泊系统锚泊线的动张力随激励幅值和激励频率的变化关系及产生冲击张力的影响因素做了探讨。动张力其他影响因素，如锚泊线绳长、刚度等，以及冲击张力时，激励幅值和频率之间的量化关系等问题今后将继续深入研究。