用高中知识简化求解多狗追击问题
王 菁 华正和
(淮阴师范学院物理与电子电气工程学院 江苏淮安 223300)
追击问题是一种典型的物理问题,也是高中物理竞赛的典型题目,其中一个有趣的例子是“多狗追击”:开始时,几条狗分别处于正多边形的顶点上,吹哨放狗,狗以相同不变的速率相互追逐。文献[1-6]分别利用不同的方法和思路,求出了狗追击所需时间、追击经过的总路程。文献[1]用到了复变函数和微积分,文献[2-4]用到了极坐标和微积分,文献[5,6]只用到了微积分。几位作者虽顺利解决了多狗追击问题,但都用到了高等数学知识,这样的解题方法和思路显然不适合高中生。
本文采用先易后难的思路,首先处理三狗追击问题,通过对问题几何关系的分析,用相对浅显的高中知识求出狗追击所用时间、狗追击经过的总路程及追击过程中狗的加速度大小,再将此分析方法扩展到N狗追击问题。
一、三狗追击问题
如图1所示,初始时,三狗分别位于正三角形的顶点A、B、C。随着三狗相互追击,正三角形不断旋转,旋转过程中,三角形边长也逐渐变小,直至为0。
(一)狗追击所需时间
1.法一
设经过很短的时间Δt,三角形旋转缩小为A1B1C1,此时边长A1B1长度为L1。边长AB变为A1B1,缩短来源于A点处狗的贡献和B点处狗的贡献。其中,A点处狗的贡献为vΔt,B点处狗的贡献为vΔtcos∠B=1/2vΔt。由此得
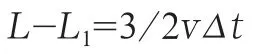
同理,再经过Δt,此时边长变为L2,有
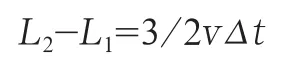
由此类推
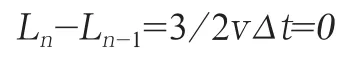
由此得
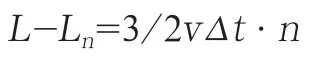

图1 三狗追戏问题
追击结束,三角形边长Ln=0,得追击所用时间

2.法二
设经过Δt,三角形旋转缩小为A1B1C1。此时,三角形顶点A至中心的距离由k0减小为k1,如图1所示。其长度减小完全来源于A点处狗的贡献。

同理得
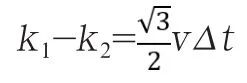
……
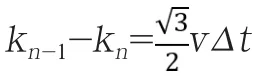
由此得
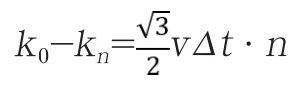
追击结束,三角形顶点到中心的距离kn=0,考虑到得追击所用时间
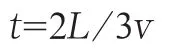
(二)狗追击加速度
如图1所示,追击过程中,经过时间Δt,边长AB旋转变为A1B1,转过的角度为Δθ。因为Δt很小,所以Δθ也很小,有

由于追击过程中狗的速率不变,故狗追击过程中的加速度就等于向心加速度
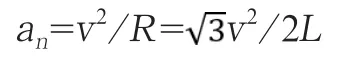
由此可见,随着三角形边长的减小,此加速度与边长成反比例增加。
(三)狗追击走过的总路程
二、四狗追击问题
如图2所示,初始时,四狗位于正四边形的顶点,正四边形边长为L。随着狗相互追击,正四边形不断旋转,旋转过程中,四边形边长也逐渐变小,直至为0。
(一)狗追击所需时间
1.法一
设经过Δt,四边形旋转缩小为A1B1C1D1。此时,边长A1B1长度为L1。AB变为A1B1,边长缩短同样来源于A点处狗的贡献和B点处狗的贡献。其中,A点处狗的贡献为vΔt,B点处狗的贡献为0。

同理可得


图2 四狗追戏问题
追击结束,四边形边长Ln,故L=vt,得追击所用时间
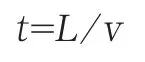
2.法二
设经过Δt,正四边形顶点A至中心的距离由k0减小为k1,如图2所示。其长度减小完全来源于A点处狗的贡献。

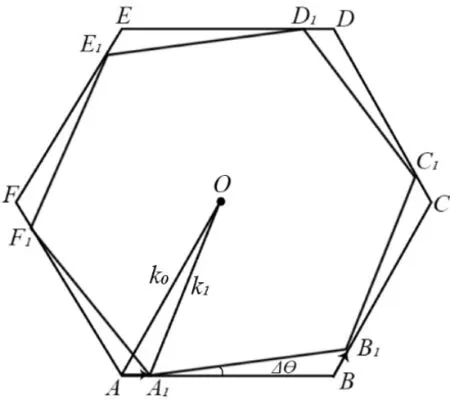
图3 N狗追戏问题
同理可得

追击结束,四边形顶点到中心的距离kn=0,故由此得追击所用时间

(二)狗追击加速度
同理可得经过时间Δt,边长AB旋转的角度Δθ,有
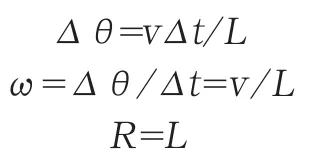
故

(三)狗追击走过的总路程

三、N狗追击问题
正N边形用正六边形示意,如图3所示。初始时,N狗分别位于正N边形的顶点,正N边形边长为L。随着狗相互追击,正N边形不断旋转。旋转过程中,N边形边长也逐渐变小,直至为0。
(一)狗追击所需时间
1.法一
设经过Δt,N边形旋转,此时的边长A1B1长度为L1。边长AB缩短为A1B1,缩短来源于A点处狗的贡献和B点处狗的贡献。其中,A点处狗的贡献为vΔt,B点处狗的贡献为

同理得

追击结束,N边形边长Ln=0,故

得追击所用时间
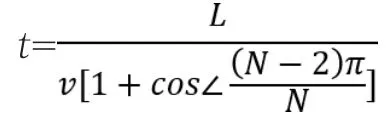
2.法二
设经过Δt,正N边形顶点A至中心的距离由k0减小为k1。其长度减小完全来源于A点处狗的贡献,

同理得
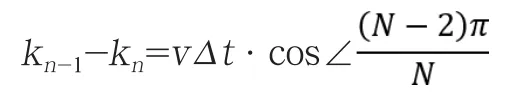
追击结束,N边形顶点到中心的距离kn=0,考虑到由此得追击所用时间

(二)狗追击加速度
同理可得经过时间Δt,边长AB旋转的角度Δθ,有

故狗追击加速度
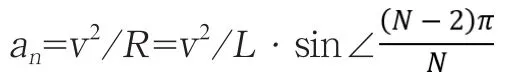
(三)狗追击走过的总路程


