转“识”成“智”：儿童数学实验的内容选择及教学策略

【摘要】数学实验是儿童喜欢的学习方式。在数学实验课程的实施过程中，要关注内容选择和教学策略。从儿童的认知规律和学习动力机制视角来看，内容选择要体现“做”与“思”相结合的原则，具有层次性、具身性、情境场域性和活动性;教学策略要从确立规程、创设教学空间、沉浸体验、辨别真伪四个方面进行優化。

【关键词】数学实验;学习场域;教学策略

【作者简介】武建军，高级教师，主要研究方向为小学数学教学设计，江苏省特级教师，江苏省教育科研先进个人。

【基金项目】江苏省连云港市教育科学“十三五”规划2018年度重点课题“小学数学实验资源的建设与开发研究”（C/2018/09/172）

数学实验是学习数学的一种重要方式，被广泛应用于中学和大学的数学学习中。在小学数学教材中，依据学段的特点，也存在数学实验的内容，并且《义务教育数学课程标准（2011年版）》对数学实验也提出了相应的要求。然而，从数学课程的属性及心理学的视角来看，小学（儿童）数学实验与中学和大学数学实验存在极大的差别。把握好儿童数学实验，需要关注其内容的结构化选择，以及依据内容进行的程序性教学活动，即通过儿童数学实验的文化表达，促进儿童认知的经验生长，达成转“识”成“智”的素养目标。

一、儿童数学实验的基本内涵

儿童数学实验是儿童学习数学的重要方式，如人教版数学教材中的“数学乐园”、北师大版数学教材中的“数学好玩”等特色内容的设计，说明儿童数学实验是客观存在的教学活动。而儿童数学实验的演绎过程可通过教学具、几何画板、计算机模拟等工具来实现。

笔者在实践中专注儿童数学实验研究，在理论和实践的指导下总结出其内涵。儿童数学实验是指让儿童借助一定的物质仪器或技术手段，通过对实验素材进行数学化的操作来学（理解）数学、用（解释）数学或做（构建）数学的一类数学学习活动[1]。其主要特征是学段性、操作性、体验性、探究性和创造性。

二、儿童数学实验内容选择的基本原则

儿童数学实验强调儿童在数学学习过程中的实践与感悟。从儿童的认知规律和行为特点出发，让尝试、试探、想象成为儿童学习命题的主要方式，促进儿童行为技能与智力技能的双向融合。

1内容选择的层次性划分

按照年龄特征及学段内容，儿童数学实验学习内容可划分为三个层次：第一，尝试实验（一、二年级）;第二，试探实验（三、四年级）;第三，想象实验（五、六年级）。其中，第一层次的重点是培养儿童尝试“做”的意识，让儿童[JP+1]在动手操作中获得学习的快乐，并且让“做”成为儿童的一种学习习惯，做中学，做中说，培养儿童的数学表达能力。第二层次的重点是建立“做”与“思”相融合的实验模式，促进儿童行为技能和智力技能的相互转化，建立初步的求证意识，形成初步解决问题的能力。第三层次的重点是培养儿童的探究意识和想象能力，通过数学实验的学习方式，积累儿童的数学活动经验，开发儿童的数学学习潜能，激发儿童的创造力。

2内容选择的具身性体现

具身认知理论认为，认知的种类和特征与身体的结构有关，人是进化的产物，是由环境塑造的，身体和环境是联合体，而思维与身体是不可分割的，没有离身的思维，同时身体感官通道的撷取和组织为思维提供信息，而认知动能也离不开身体动能[2]。儿童学习的基本特征是模仿和尝试，是基于观察和注意的做中学，而这些恰好是儿童数学实验学习的本质所在。如“看一看”“做一做”“想一想”“说一说”是具身认知在数学实验中的教材位移;手脑并用是具身认知在数学实验中的形式位移;做学同构、做思共生是具身认知在数学实验中的智识转换。

3内容选择的情境场域性

库尔特·勒温提出，人的行为取向取决于内部立场和环境立场的交互作用。儿童数学实验学习和传统的课堂相比具有不同的情境场域性，它的物理空间经过了标准化的建设和交互技术的改造，学习要素的关系空间发生了变化。因此，内容选择要和情境场域相融合，让儿童在学习的过程中能够真正运用探究、合作的学习方式。

4内容选择的活动性渗透

儿童数学实验学习是围绕数学活动展开的，因此，内容选择首先要考虑数学活动。在数学活动的引领下，学生、教师、场域、学习材料四要素相互作用，构成数学实验学习的关系空间，形成数学实验学习的基本结构。儿童是数学实验的主体，在学习要素之中，儿童的主体性作用需要放在显著的位置。从数学实验的本质来看，儿童的主体性是通过活动目标的设置，以及师生关系的作用来实现的。在典型的场域内，儿童通过主体活动，深入体验，产生平衡和失衡的心理反应，并引起行为变化。

三、儿童数学实验的教学策略

儿童数学实验从教的方式来说，充分体现了学习主体的互动性及其合作学习的有效性;从学的方式来说，体现了兴趣与主动性的结合，使儿童的主体意识在探究情境中得以唤醒。数学实验教学立足于知识的“来龙去脉”，构建完整的“教学过程链”，培养学生反思、批判、创新的思维，以及应用假设、猜想、实证等诸多方法，达到发展学生数学素养的目的。

1“立”规程，明确数学实验教学的实施路径

教学规程指在一定的教育教学理论或理念指导下，引导教师转变教学行为的规则、要求及操作策略，它能为教师教学行为的转变提供一系列规范的操作指南，因而具有导向作用[3]。儿童数学实验教学作为一个新的教学实验命题，确立规程是教学得以顺利实施的基本保障。

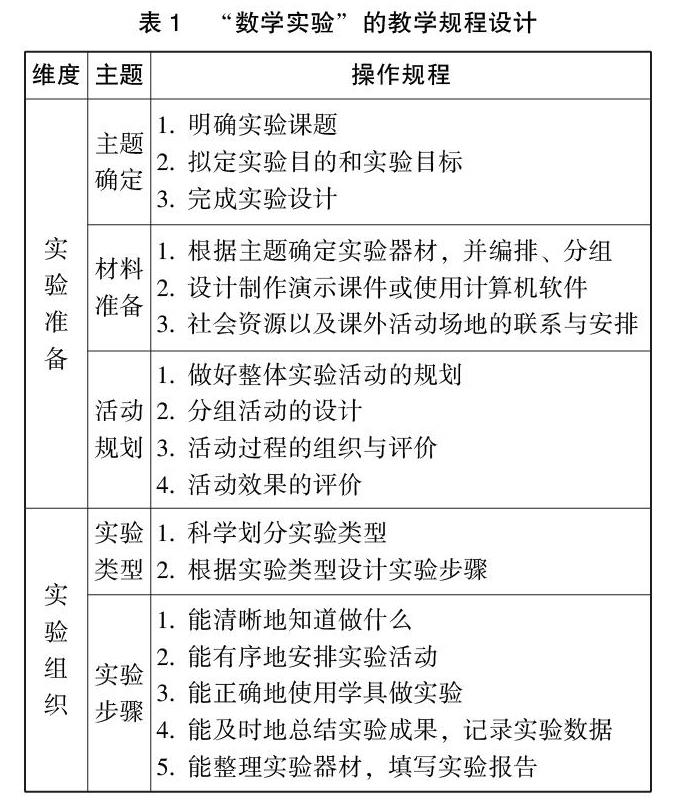
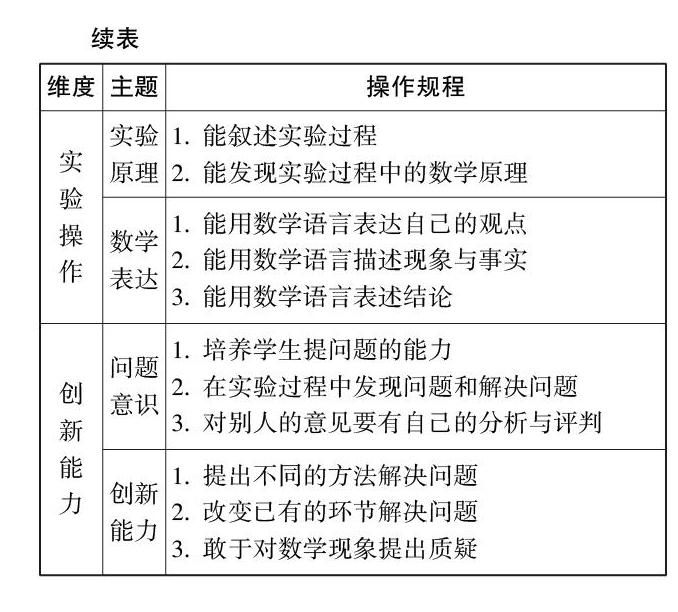
“数学实验”的教学规程设计如下（见表1）。

数学实验课程立足于实验准备、实验组织、实验操作、创新能力四个维度，确立九个主题，制订二十八条操作规程，指向数学实验教与学的互通，开拓了数学实验课程的实施路径。

2“建”场域，创设数学实验教学的两个空间

基于库尔特·勒温的场动力理论，数学活动的开展依赖于其动力系统的良性运行。而“场域”是动力系统中的关键要素，在实践中主要体现在重构数学活动的物理空间和关系空间上。

[JP+1]例如，对于物理空间的改造，一是改造普通教室。包括添置学具柜、增设展示墙、装备交互式实验学习设备，学生自备数学实验操作展示板等。通过对教室环境的改造使数学实践操作成为可能和常态。二是建立数学专用室。包括建立E学习体验室，增加包含软件的平板、VR技术等，为数学实验学习提供“交互学习”平台，提高对抽象概念和空间观念的体验性;建立数学操作室，通过动手实践，借助信息化工具及材料创造出学习成果，为学生积累数学经验提供物质基础;建立数学实验室，通过AR技术丰富交互式数学学习新体验，搭建数学探究的学习平台。

再如，对于关系空间的再造，一是对儿童数学实验的四对要素关系的梳理，即对生生之间的伙伴式关系、师生之间的对话式关系、人与环境之间的沉浸式关系、环境与学习材料之间的融合式关系的梳理。二是基于关系落地的观察量表的设计。三是基于行为“靶向”改进的观察报告的生成。（见表2）

两个空间的优化，突出了“场域”在儿童数学实验中的支撑作用，以及学生、教师、学习材料、环境四要素的相互作用，引发儿童在实验场域中的认知冲突和矛盾、群体间的竞争与合作、对过程的质疑与反思，诱发数学活动动力机制的生成，持续激发儿童的学习行为。

3“做”实验，引发数学实验学习的沉浸体验

人们在做某件事时，会尽力满足自我选择和自主决策的需要，且因内在压力而采取的行为比因外在压力而采取的行为更容易让人满足。学习中的沉浸体验状态是指人们在生命中全身心投入某事，并尽情享受其带来的快乐的时刻[4]。也即行动者和行动能够达成合二为一的专注状态，凭借的是内在动机而不是外在动机。

数学实验无论作为课程内容还是作为教与学的方式，均符合人类认知和学习的一般规律，也符合儿童心理发展的基本特征，是完全可行的。儿童数学实验，充分照顾儿童的个体差异，能使儿童大脑各个区域的功能得到充分发挥，促进儿童的全面发展。注重操作与实践，变“听数学”为“做数学”，变“看演示”为“动手操作”，变“机械接受”为“主动探究”。这样，儿童的主体意识得到了发展，思维能力得到了提升，拥有了创新的机会。

从儿童的学习心理动因分析，沉浸体验在儿童数学实验过程中是可以发生的。例如，数学实验“测量土豆的体积”源于苏教版小学数学六年级实验教材，与儿童数学实验的主题非常契合。因为土豆是不规则形体，选用规则形体的计算方式是无法得出结论的，所以只通过直观演示和教师讲解都不能有效地促进學生对问题的深入理解。因此，数学实验就成为解决问题的路径选择。首先，让学生自主准备材料，观察实验物体，选择实验用具;其次，让学生进行分组实验，探究土豆体积的测量方法，并在学习单上记录实验过程;最后，完成实验报告，发现数学方法，形成数学结论。学生在充分讨论的基础上进行实验，选用土豆和长方体水槽，将土豆浸入水中，运用测量工具，测量水的高度变化，对比发现土豆体积与水体积的关系，得出土豆体积的测量方法。一系列的实验过程，让学生沉浸在活动的氛围中，有目的、有秩序、有思考、有挑战，整个过程也是学习发生和发展的历程。

以上活动表明，儿童在学习中是可以进入沉浸状态的，关键是情境要能激发儿童的主体内驱力。数学实验从场域、方式、目标等出发，能达成主体和行动的合二为一，能持续激发儿童的学习动力。

4“辨”真伪，反思数学实验学习的育人价值

当前的小学数学教学，从课程设计和教学实践来看，知识“权威性”致使学生无条件接受的现象比较普遍，对数学结论“证实”多，“证伪”少，抹杀了知识的创造过程。而数学实验学习让学生经历完整的知识形成过程，感受知识从不确定性到确定性，在猜想、证实和证伪中生成数学经验。

例如，对于苏教版小学数学四年级上册教材的内容“过直线外一点与这条直线的连线中，垂线段最短”这个片段的教学，用数学实验的方法，可以这样安排。首先，从直线外的一点，向已知直线画或折多条线段（包括垂线段）。其次，用尺子量一量这些线段的长度并记录下来。最后，比较这些线段的长度，看看有什么发现，并将结论写出来。学生通过测量发现“垂线段最短”的结论。其实，这个过程就是“证实”数学结论的过程。然而，这样的教学所获得的结论，只能是学生的“视觉结论”。学生可能还会追问“为什么是垂线段最短？”“是否存在比这条垂线段还短的线段呢？”等问题，而这些问题才真正指向了问题的本质。

教师可以相机开展下一段教学。教师提问：“假设存在这样一条比垂线段还短的线段，你能画出来吗？”学生通过观察和操作后，认为不好画出这样一条线段，但还是不理解“为什么是垂线段最短”。这时，教师进一步引导学生进行实验操作，以直线外一点为圆心，以垂线段为半径，画一个圆（如图1）。引导学生观察并提问：“你有什么发现？”这时，学生才恍然大悟，和垂线段相等或比它短的线段，都在圆上或圆内。因此，不存在比这一条垂线段还短的线段。

这个教学片段，将“证实”和“证伪”结合起来，使学生在数学学习中不仅“知其然”还“知其所以然”。两次操作实验，经历了知识的发生和发展过程，使学生形成了完整的认知理念，学生的理性思维水平得以提升。

总之，儿童数学实验是培养儿童动手和创新能力、转变儿童学习方式、积累数学活动经验的载体和平台。完善儿童数学实验的内容，探究儿童数学实验的教学策略，是进一步提升儿童数学素养的有效路径。

参考文献：

[1]武建军.数学实验：小学生实践操作与数学思维的视界融合[J].江苏教育，2015（1）：23-25.

[2]叶浩生.身体与学习：具身认知及其对传统教育观的挑战[J].教育研究，2015（4）：104-114.

[3]吴永军.教学规程：将教学理念转化为教学行为的指南[J].课程·教材·教法，2015（5）：21-27.

[4]阿伦兹.学会教学：第九版[M].丛立新，阿不力孜，张建桥，等译.北京：中国人民大学出版社，2016.