钢桥面顶板纵肋焊接细节疲劳裂纹扩展模拟方法研究
矣志勇

摘要:钢桥面顶板纵肋焊接细节是正交异性钢桥面板中最重要的疲劳易损细节之一,探究其疲劳裂纹扩展特性有助于深刻认识其疲劳性能。当前常用的疲劳裂纹扩展模拟方法主要包括以断裂力学理论为基础的二维分析方法和三维分析方法两类。本文分别通过二维和三维断裂力学分析方法对于顶板纵肋焊接细节重要疲劳破坏模式的疲劳裂纹扩展数值模拟、疲劳裂纹疲劳寿命和扩展特性等关键问题进行了对比研究。
Abstract: Rib-to-deck welded joints are one of the most important fatigue details in the orthotropic steel decks. Studying fatigue crack propagation characteristics of rib-to-deck welded joints can help to recognize its fatigue performance deeply. For the fatigue crack propagation simulation method used in rib-to-deck welded joints, there are currently two fracture mechanics analysis methods, which are 2D fracture mechanics analysis method and 3D fracture mechanics analysis method. Taking the important fatigue damage mode of rib-to-deck welded joints of the steel deck as the research object, fatigue crack propagation numerical simulation, fatigue life and fatigue crack growth characteristics and other essential problems are studied using 2D and 3D fracture mechanics methods.
關键词:桥梁工程;钢桥面板;顶板纵肋焊接细节;断裂力学;裂纹扩展模拟方法;疲劳寿命
Key words: bridge engineering;steel bridge decks;rib-to-deck welded joints;fracture mechanics;crack propagation simulation methods;fatigue life
中图分类号:U441+.4 文献标识码:A 文章编号:1006-4311(2020)04-0153-03
0 引言
正交异性钢桥面板是大跨度桥梁的首选桥面板结构[1]。针对顶板纵肋焊接细节疲劳裂纹,可采用二维和三维断裂力学分析方法对其进行研究。此处以顶板纵肋焊接细节从焊根萌生的疲劳裂纹为研究对象,分别基于二维、三维断裂力学分析方法进行了疲劳裂纹扩展的数值模拟,对两类分析方法的疲劳裂纹疲劳寿命和扩展特性进行了对比研究。
1 疲劳裂纹扩展模拟方法及关键问题
1.1 两类疲劳裂纹扩展模拟方法
当前常用的二维分析方法首先建立钢桥面板整体模型,整体模型中不含缺陷,之后在整体模型的基础上建立用于裂纹分析的平面应变子模型,在平面应变子模型的焊根位置引入初始裂纹,即可采用二维分析方法对顶板纵肋焊接细节典型疲劳裂纹进行数值模拟。三维分析方法针对研究的钢桥面板建立实体单元模型来实现典型疲劳裂纹三维扩展模拟。
1.2 裂纹扩展数值模拟的关键问题
裂纹扩展方向对于应力强度因子的计算具有重要的影响,对于二维分析方法,裂纹扩展方向只需计算出裂纹尖端点的扩展角度即可确定,对于三维分析方法,裂纹扩展方向通过计算各裂纹尖端点的扩展角度来确定,两种分析方法的裂纹扩展角度依据最大周向应力理论[2],由下式求得式中,ΔKⅠ、ΔKⅡ为Ⅰ型、Ⅱ型裂纹应力强度因子幅值。
二维分析方法可采用等效应力强度因子来计算裂纹扩展速率和疲劳寿命。等效应力强度因子ΔKeff计算公式[2]如下,公式中的符号含义与式(1)相同。对于三维分析方法,等效应力强度因子参照规范BS7910[3]给出的计算公式求解,式中,υ为泊松比,本文取0.3;ΔKⅢ为Ⅲ型裂纹应力强度因子幅值,其余符号含义与式(1)相同。
针对疲劳裂纹扩展阶段数值模型的研究,Paris定律[4-5]认为在裂纹扩展速率与裂纹尖端应力强度因子之间存在如下关系:
2 方法的实现及其试验验证
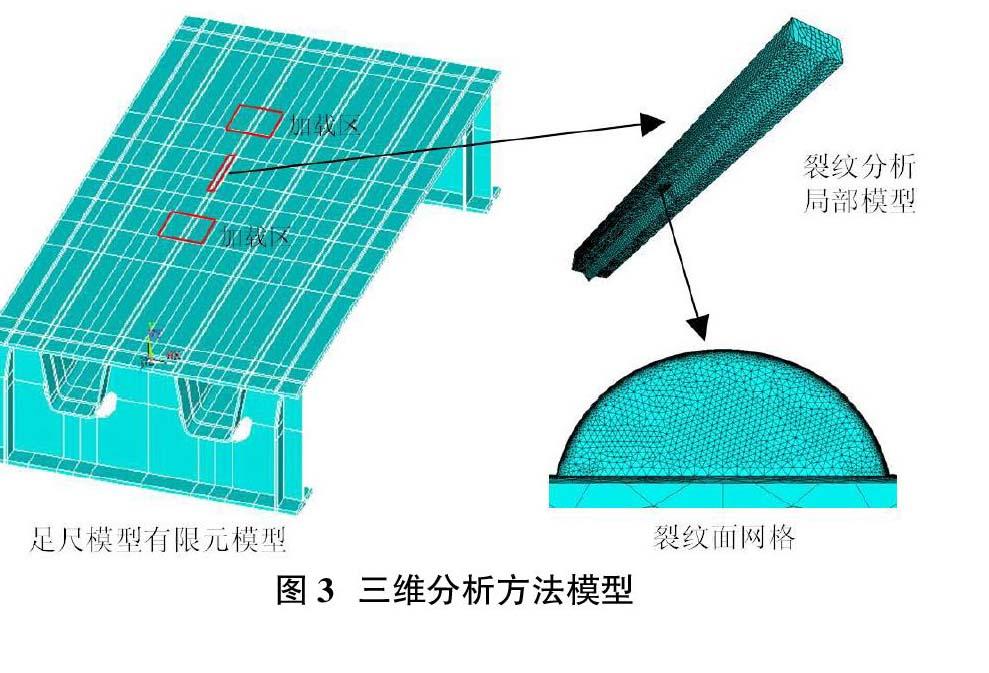
本文以某顶板纵肋焊接细节疲劳试验的足尺试验模型进行两类分析方法的疲劳裂纹疲劳寿命和扩展特性对比研究。该疲劳试验完成后,采用超声探伤检测方法,确定典型疲劳裂纹出现在顶板纵肋焊缝的焊根部位,该裂纹沿焊长度方向及顶板厚度方向扩展,对裂纹最深处断面进行切片可观察到如图3所示焊根位置处的典型疲劳裂纹,该断面裂纹沿顶板厚度方向扩展深度为4.7mm,与该裂纹相对应的加载次数为120.1万次。基于该疲劳试验,本文分别建立二维分析方法模型与三维分析方法模型对两类分析方法的疲劳裂纹疲劳寿命和扩展特性进行了对比研究,有限元模型建立方法如下文所述。
2.1 二维分析方法模型
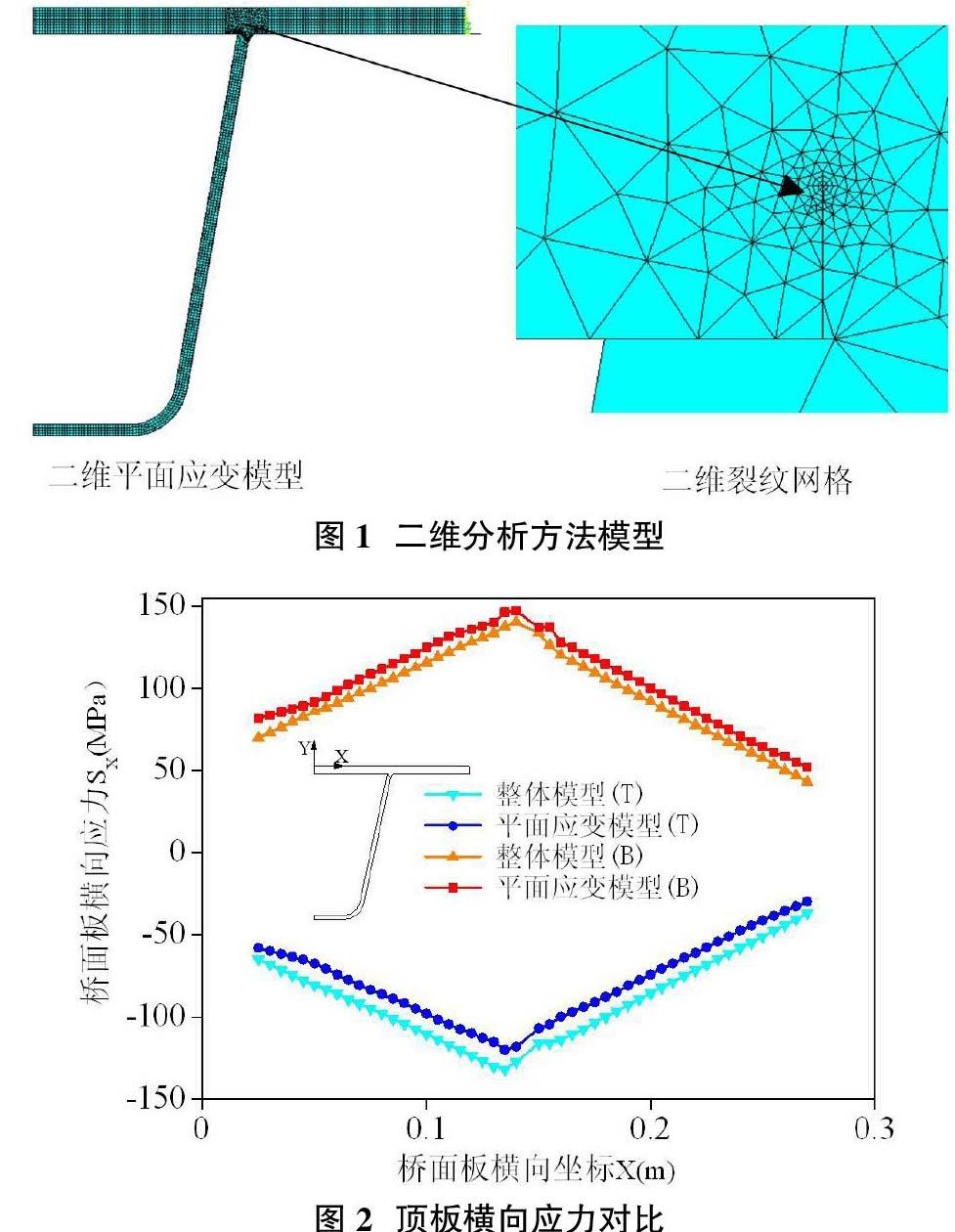
二维分析方法以图3所示三维分析方法中建立的不含裂纹ANSYS有限元模型为整体模型,建立如图1所示平面应变子模型,模型采用PLANE183单元建立,裂纹尖端周围建立一圈6节点三角形奇异单元模拟裂纹尖端点周围应力场的奇异性。
同时,为验证平面应变模型的合理性,取整体模型顶板横向应力与平面应变模型顶板横向应力进行对比,如图2所示,(T)、(B)分别代表顶板上、下缘,可见在不含缺陷的初始状态,二者应力状态吻合较好。
2.2 三维分析方法模型
根据前文所述疲劳试验的足尺试验模型建立的ANSYS有限元模型如图3所示,有限元模型采用实体单元SOLID95建立,裂纹前缘周围第一排单元为15节点楔形奇异单元,用于模拟裂纹尖端附件应力场的奇异性,采用与试验相同的荷载进行计算分析。
2.3 模拟方法的试验验证
采用二维、三维分析方法计算得出该疲劳裂纹的疲劳寿命如表1所示,并与试验结果进行比较。计算结果表明:二维分析方法得出的疲劳寿命与试验结果相差较大,三维分析方法计算出的疲劳寿命与试验结果相差较小,三维分析方法预测的疲劳寿命更为准确。
3 两类方法分析结果的对比研究
3.1 应力强度因子
对顶板纵肋焊接细节典型疲劳裂纹二维、三维扩展进行模拟,得到关注点即二维裂纹尖端点与三维裂纹前缘最深点等效应力强度因子随裂纹扩展的变化规律如图4所示。
研究结果表明,对于顶板纵肋焊接细节典型疲劳裂纹二维分析方法,裂纹沿顶板厚度方向扩展至15%板厚之前,二维分析方法与三维分析方法得出的关注点等效应力强度因子误差在10%以內,随着裂纹的进一步扩展,二维分析方法得出的关注点等效应力强度因子始终保持逐渐增大的趋势,且与三维分析方法得出的关注点等效应力强度因子变化规律存在明显的区别。二维分析方法采用的平面应变模型边界条件来自于与之对应的不含缺陷的整体模型中,其在裂纹扩展模拟过程中无法考虑整体结构效应对裂纹周围局部受力机制的影响,针对复杂结构在复杂受力状态下顶板纵肋焊接细节典型疲劳裂纹扩展的模拟,二维分析方法不容易得到理想的计算结果。
3.2 裂纹扩展速率
二维分析方法和三维分析方法得到的裂纹关注点扩展速率曲线如图5所示。
研究结果表明,二维裂纹扩展模拟得到的裂纹关注点扩展速率随裂纹扩展始终在增大,没有出现裂纹扩展速率下降段,三维裂纹扩展模拟得到的裂纹关注点扩展速率与二维扩展模拟得到结果有明显区别。三维裂纹扩展模拟得到的裂纹关注点扩展速率呈现先增大后减小的规律,裂纹沿板厚方向扩展至一半顶板厚度之前,裂纹关注点扩展速率逐渐增加,之后裂纹关注点扩展速率随裂纹扩展逐渐减小。裂纹扩展速率的变化与应力强度因子变化规律直接相关,二维分析方法与三维分析方法关注点应力强度因子变化规律的区别使得两种方法得出的裂纹关注点扩展速率变化表现出不同的趋势。
4 结论
通过对基于断裂力学的顶板纵肋焊接细节典型疲劳裂纹扩展模拟方法进行研究,进一步对该细节典型疲劳裂纹在二维分析方法和三维分析方法下得出的裂纹疲劳寿命、应力强度因子、扩展速率变化规律进行了对比分析,得出如下结论:
①二维分析方法预测的疲劳裂纹疲劳寿命低于三维分析方法得出的预测结果,三维分析方法得出的疲劳寿命更接近于试验测试值。
②二维分析方法不能准确模拟典型疲劳裂纹扩展过程中裂纹面偏转,对Ⅱ型、Ⅲ型开裂模式考虑不足,该方法采用的平面应变模型边界条件取自与之对应不含缺陷的整体模型,进行裂纹扩展模拟时无法准确反应实际裂纹扩展过程中裂纹周围区域应力重分布情况。
③采用三维分析方法可以准确模拟该细节典型疲劳裂纹扩展过程中裂纹面角偏转,将典型疲劳裂纹作为复合型疲劳裂纹分析,可以获得更为准确的裂纹扩展特性,其对复杂结构在复杂受力状态下的疲劳裂纹扩展模拟具有更好的适用性。
④对于现有的二维分析方法,在深入研究典型疲劳裂纹开裂过程中裂纹周边区域变形及局部刚度变化规律的基础上,提出修正边界条件的二维分析方法是下一步研究工作的一个重点。
参考文献:
[1]孟凡超,张清华,苏权科,等.正交异性钢桥面板抗疲劳关键技术[M].北京:人民交通出版社,2014.
[2]Tanaka K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis[J]. Engineering Fracture Mechanics, 1974, 6(3):493,IN13,499-498,IN14,507.
[3]BS 7910:2013+A1:2015,Guide on methods for assessing the acceptability of flaws in metallic structures[S].
[4]Paris P C, Erdogan F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4):528-533.
[5]Wiegrebe W. Fatigue assessment of welded joints by local approaches, Second edition. [M]. 2010.

