螺旋弹簧的减重试验设计*

熊志远，宋瑞祥，吴 瑞，赵 娜，赵 阳

(北京市劳动保护科学研究所，北京 100054)

0 引 言

螺旋弹簧是环形弹簧、碟形弹簧、扭杆弹簧等各类弹簧中应用最广泛的一类弹簧。在车身与车轮、动力设备与基础之间安装螺旋弹簧能够起到缓冲减振的作用；凸轮机构中的压紧螺簧、内燃机中的阀门螺簧等均能够起到控制机械运动的作用；另外，弹簧秤中的螺旋弹簧可用来测量力的大小。减轻螺旋弹簧的重量不仅能节省材料，还能给装卸、运输、使用等带来便利。此外，螺旋弹簧是汽车悬挂系统的重要组成部分，减轻其重量能促进汽车整备质量的降低，有利于提高汽车动力性能、减少燃料消耗、降低排气污染。

目前，螺旋弹簧的减重设计主要有结构优化和运用轻质、高性能复合材料。王建中等[1]利用基因遗传算法，对一内燃机气门螺旋弹簧进行模糊优化设计，结果弹簧减重29.7%。刘昌领等[2]应用混合遗传模拟退火算法，对某采油树阀门机构内部一螺旋弹簧进行优化设计，优化结果与传统设计法相比，弹簧减重17.5%。薛耀勇等[3]运用Matlab对管道机器人中的螺旋弹簧进行了优化设计，结果弹簧减重10%。杨峰[4]应用遗传算法，在保持刚、强度性能不变的情况下，对汽车悬架螺旋弹簧进行了优化仿真，结果簧丝直径、簧圈平均直径和有效圈数分别减小6.07%、7.35%、16.28%。时培成等[5]利用VC++6.0对由两螺旋弹簧串联而成的变刚度悬架弹簧进行了优化运算，根据优化前、后簧丝直径、簧圈平均直径、有效圈数，计算出变刚度弹簧减重15.64%。

詹博文[6]等对车用复合材料螺旋弹簧进行了优化设计，优化后的弹簧比金属弹簧减重34.4%。杨永宝等[7]、金达锋等[8]对碳纤维复合材料螺旋弹簧的刚、强度性能进行了理论预测与仿真研究。Zebdi等[9]与Azzam[10]分别基于多目标优化设计软件，对复合材料螺旋弹簧的最小质量与最大刚度进行了优化设计。Calm[11]研究了任意形状的复合材料螺旋弹簧的动态行为。Kim等[12]将模塑技术和纺织技术相结合制备出了复合材料螺旋弹簧，并导出了弹性常数。隋刚等[13]制备了玻璃纤维复合材料螺旋弹簧，并探讨了加工工艺及结构参数对弹簧的弯曲回弹力、回复率、拉伸性能等的影响。笔者对螺旋弹簧的减重设计不同于现有的结构优化，主要探讨空心簧丝螺旋弹簧刚、强度性能与重量等之间的变化关系，在保证弹簧刚、强度性能不变的情况下，减去较多重量，为螺旋弹簧减重设计提供一种新方法。

1 空心簧丝螺旋弹簧刚强度

图1是空心簧丝螺旋弹簧在P力作用下进行压缩时的示意图，表1是该弹簧的相关参数。簧丝内、外径分别用di、do表示，下标“i”与“o”分别为英文单词“inside”和“outside”的第一个字母。弹簧自由时，螺旋角α=5°；随着压力P由0逐渐增加，弹簧被压缩，相邻簧丝之间间隙变小，α随之下降。实心簧丝螺旋弹簧受压时最大剪应力与刚度均有经典的理论分析[14]，此文将先对空心簧丝螺旋弹簧受压时的最大剪应力及刚度进行理论推导。

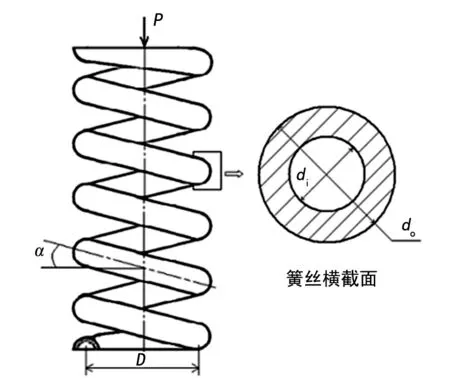
图1 空心簧丝螺旋弹簧示意图

如图2所示，是以簧丝任意横截面截取的弹簧上部分。α≤5°时，可认为簧丝横截面与簧圈轴线在同一平面内。由截取部分的受力平衡条件，簧丝截面上应有一个剪力Q和一个力偶矩T，且Q=P，T=PD/2。

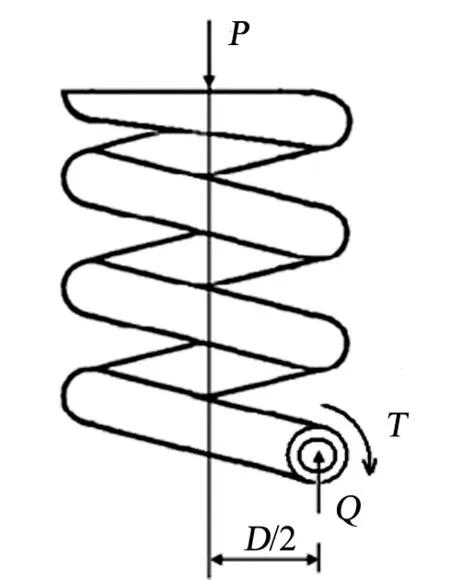
图2 以簧丝任意横截面截取的弹簧上部分

剪力Q可认为在簧丝横截面上均匀分布，见图3(a)，其剪应力τ1为：

(1)

表1中，簧丝直径9 mm远小于簧圈平均直径100 mm，故而可略去簧丝曲率的影响，近似用受扭直杆横截面上的剪应力[14]表示簧丝横截面上的剪应力τ2：

(2)

式中：r为横截面上应力点到圆心的距离，应力分布如图3(b)。

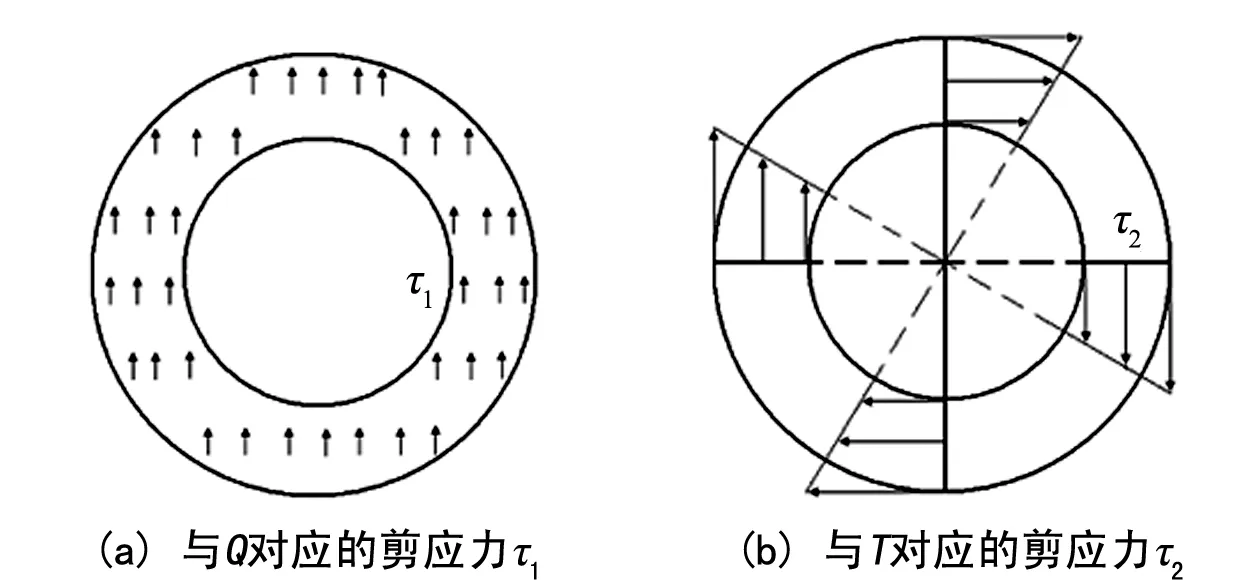
图3 簧丝横截面上剪应力分布示意图

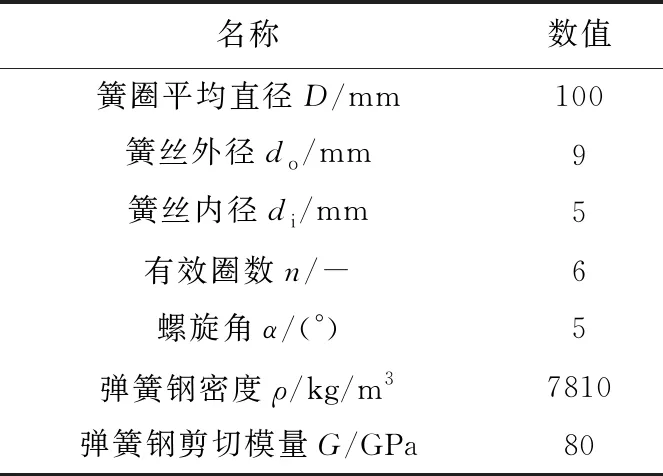
表1 空心簧丝螺旋弹簧相关参数

图3中，最大合应力位于截面最左边缘处，将r=do/2代入式(2)后，再与式(1)相加，并整理得：

(3)

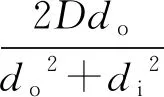
(4)

弹簧在载荷P作用下产生位移λ，载荷P对弹簧所做的功W为：

(5)

基于式(2)和图3(b)，进一步作出横截面上距圆心为r的点处的剪应力τ2，如图4所示。弹簧材料中单位体积变形能u可表示为：

(6)

整个弹簧储存的变形能U为：

(7)

式中：rdrdθ表示截面上的微分面积，ds为沿簧丝轴线的微分长度。将式(2)代入式(6)，再将式(6)代入式(7)，计算结果为：

(8)

载荷P对弹簧所做的功W等于弹簧所储存的变形能U，由式(8)等于式(5)，可得弹簧刚度为：

(9)

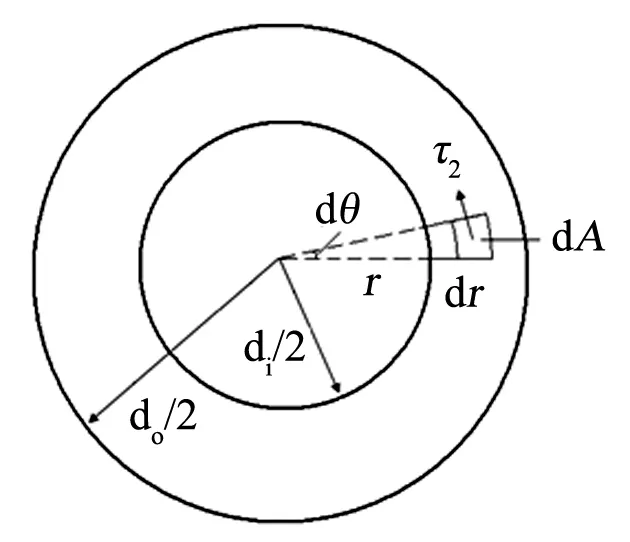
图4 簧丝横截面上距圆心为r的点处的剪应力τ2

2 螺旋弹簧的减重设计

2.1 等刚度条件下的减重设计

将表1中相关参数代入式(9)，其中只允许簧丝内径di变化，作出弹簧刚度K与簧丝内径di变化关系曲线，如图5所示。

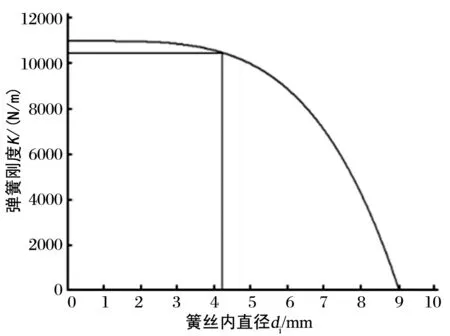
图5 弹簧刚度K与簧丝内径di的变化关系

曲线表明：随着簧丝内径的增加，弹簧刚度逐渐降低，即：在簧丝外径(9 mm)等其他参数不变的情况下，随着空心簧丝壁厚越来越薄，弹簧刚度越来越低。但是在曲线的不同区域，弹簧刚度的降低程度是不一样的：在前段，刚度下降十分平缓，而簧丝内径增加较多，即伴有较多减重；在后段，弹簧刚度显著降低。当簧丝内径di=4.256 mm时，经式(9)计算得空心簧丝弹簧刚度为10388.25 N/m，见图5中标出的相应直线，该点是刚度下降尽量小、重量下降尽量多的平衡点。

将di=0 mm及表1中相关参数代入式(9)后，并令其等于10 388.25 N/m，经计算得实心簧丝弹簧的簧丝直径为8.885 mm。等刚度的两弹簧，它们的材料、有效圈数、簧圈平均直径、螺旋角等都相同，不同的仅仅是如图6所示的簧丝横截面。

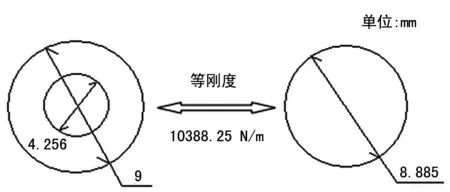
图6 等刚度下的空心与实心簧丝横截面

现有螺旋弹簧几乎全为实心簧丝结构，设计成如图6右所示的空心簧丝结构后，因空心结构位于簧丝内部，在空间上对弹簧的使用几乎不会产生影响。实心簧丝直径为8.885 mm，设计成空心结构后，簧丝外径为9 mm，直径增加0.115 mm，增加率仅为1.29 %。

空心簧丝螺旋弹簧重量计算式为：

(10)

式中：g为重力加速度，取9.8 m/s2。将do=8.885 mm、di=0 mm及表1中相关数据代入式(10)后，计算得实心簧丝弹簧重为8.936 N；同样，将do=9 mm、di=4.256 mm及表1中相关数据代入式(10)后，计算得空心簧丝弹簧重为7.118 N，减重1.818 N，减重率20.34%，减重较为明显。

2.2 等强度条件下的减重设计

将表1中相关数据代入式(4)，其中只允许簧丝内径di变化，作出弹簧最大剪应力τmax与簧丝内径di的变化关系，如图7所示。曲线表明：随着簧丝内径增加，最大剪应力逐渐升高，即：随着空心簧丝壁厚越来越薄，强度逐渐降低。在曲线前段区域，最大剪应力上升十分平缓，重量下降较多；在后段区域，最大剪应力急剧增加。当簧丝内径di=4.204 mm时，经式(4)计算得空心簧丝弹簧强度为293.57 MPa，见图7中标出的相应直线，该点是强度下降尽量小、重量下降尽量多的平衡点。

将di=0 mm及表1中相关参数代入式(4)后，并令其等于293.57 MPa，经计算得实心簧丝弹簧的簧丝直径为8.855 mm。等强度的两弹簧，其它参数均相同，不同的仅仅是如图8所示的簧丝横截面。

从图8可看出，将簧丝直径为8.855 mm的弹簧设计成等强度的空心簧丝弹簧后，簧丝外径为9 mm，直径增加0.145 mm，增加率仅为1.64%。将do=8.855 mm、di=0 mm及表1中相关数据代入式(10)后，计算得实心簧丝弹簧重为8.876 N。同样，将do=9 mm、di=4.204 mm及表1中相关数据代入式(10)后，计算得空心簧丝弹簧重为7.168 N，弹簧减重1.708 N，减重率为19.24%。

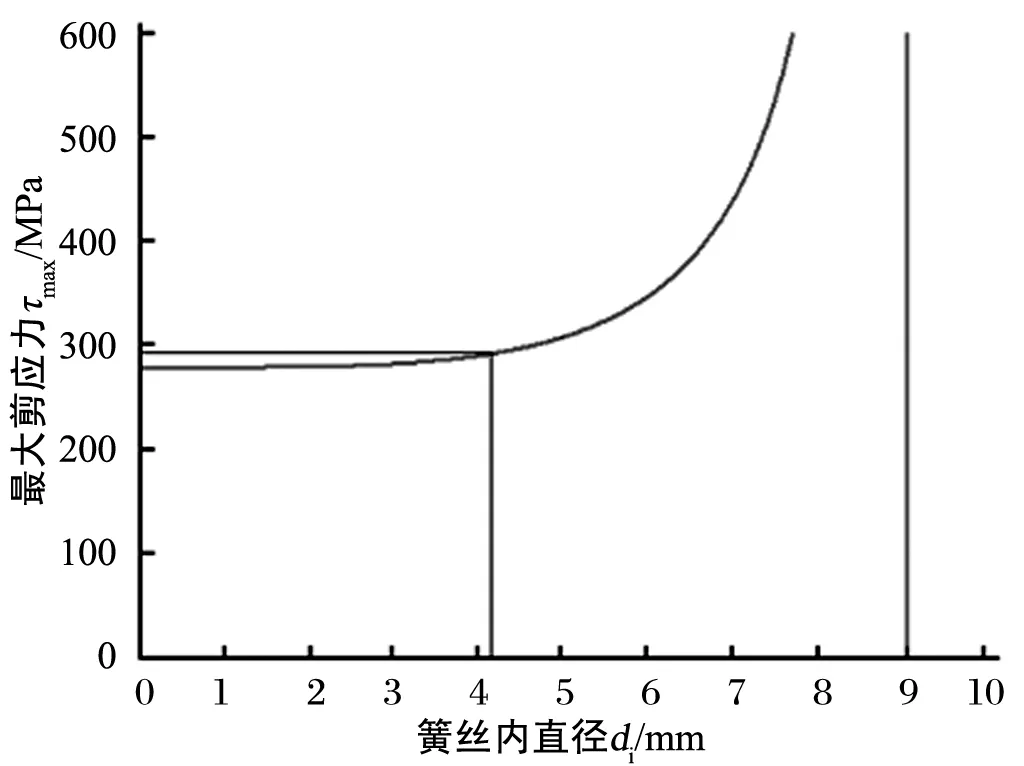
图7 弹簧最大剪应力τmax与簧丝内径di的变化关系

图8 等强度下的实心与空心簧丝横截面

3 准静态压缩试验

空心与实心弹簧钢圆棒料的长度l均可表示为：

(11)

将表1中相关数据代入后，经计算得l为1 891 mm。实心弹簧钢圆棒料横截面直径为8.885 mm，空心弹簧钢圆棒料横截面内径为4.256 mm、外径为9 mm。

弹簧的卷制采用洛阳机床厂生产的自动卷簧机，型号为Z53-14。其加工范围为：簧丝直径3～14 mm，簧圈外径15～180 mm。

在WDW-3050电子万能试验机上，分别对实心与空心簧丝螺旋弹簧进行准静态压缩试验，得到如图9所示的压力-位移曲线。

从图9中可看出，两压力-位移曲线均呈线性，即它们的斜率，也就是弹簧的刚度为一常量。经分析试验数据，得实心簧丝弹簧刚度为10 175 N/m，空心簧丝弹簧的刚度为10 058 N/m，它们与2.1节中的理论计算刚度10 388.25 N/m稍小。这可能是因为理论计算时把弹簧钢视为均匀、无缺陷的理想材料，而实际材料总是非均匀、有缺陷的，故而测量值要稍小于理论计算值。

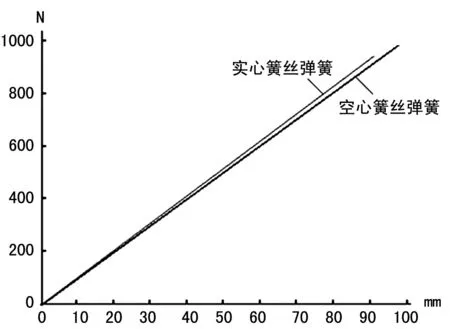
图9 准静态压缩条件下弹簧的压力-位移曲线

4 结 论

首先导出了空心簧丝螺旋弹簧受压时的最大剪应力、刚度。然后，基于所给出的弹簧实例数据，探讨了空心簧丝弹簧刚、强度性能与重量等之间的变化关系，得到如下结论：

(1) 将实心簧丝螺旋弹簧设计成等刚度的空心簧丝弹簧后，减重可达20.34%。

(2) 将实心簧丝螺旋弹簧设计成等强度的空心簧丝弹簧后，减重可达19.24%。

(3) 簧丝的空心结构以及簧丝外径的微小增加对弹簧的使用几乎没有影响。

(4) 用准静态压缩实验验证了实心与空心簧丝螺旋弹簧的等刚度性能。