基于PepS的高温核一级管道蠕变疲劳分析方法研究

龚 玮 张小春 王晓艳 薛静怡 傅 远

1（中国科学院上海应用物理研究所 上海 201800）

2（中国科学院先进核能创新研究院 上海 201800）

中国科学院上海应用物理研究所于2011年启动战略先导项目钍基熔盐堆（Thorium Molten Salt Reactor，TMSR）［1］，其核心目标为建成并运行2 MW钍基熔盐液态反应堆（Thorium Molten Salt Reactor-Liquid Fuel，TMSR-LF1）。由于TMSR-LF1回路设计温度达700℃，最高稳定运行工况温度为650℃，因此在10年的设计使用寿命中，回路管道将承受长期的高温交变载荷。管道在高温下长期服役时的最重要特性是随时间变化的蠕变-疲劳交互行为。因此，蠕变-疲劳损伤分析对高温管道完整性评定尤为重要。

ASME-ⅠⅠⅠ-5高温反应堆［2］标准中提出了通过控制应力、应变、蠕变-疲劳损伤来保证结构不发生失效的思路，并给出了相应评估方法。对于高温核一级管道，ASME-ⅠⅠⅠ-5-HBB-3650管道分析篇中规定，在线弹性材料模型适用的情况下，ASME-ⅠⅠⅠ-NB-3600［3］中的应力指数和应力公式可以用来校核高温管道的应力强度限值和应变限值。但对于蠕变-疲劳评估，一方面HBB-3650仅提到使用弹性和简化非弹性分析来满足应变和蠕变疲劳极限时可以使用NB-3600中的应力指数，却缺少相应的计算方法，无法直接依据规范完成蠕变-疲劳限值评定，进而也无法采用管道分析软件（PepS等）进行计算评定。另一方面若同承压容器一般采用ASME-ⅠⅠⅠ-5-HBBT1400进行蠕变-疲劳分析评定，需要对应力分析结果选取路径进行应力分析及线性化，但使用有限元分析软件分析（ANSYS等）时无法获得通过管道截面中心路径的应力分类和线性化结果，而使用管道分析软件（PepS等）更是不能获得应力分类和线性化结果。

为解决高温核一级管道系统结构分析与评定的工程问题［4-6］，本文依照 ASME-ⅠⅠⅠ-5-HBB-T1400 分析评定理论，通过结合管道结构在多载荷组合作用下的管道截面应力状态解析解进行管道截面应力分析及线性化，并将结果与有限元数值解进行误差分析，结果基本一致。随后利用管道分析软件PepS对TMSR-LF1回路管道进行应力分析，提取管道载荷，并基于上述评定方法得到了TMSR-LF1的蠕变-疲劳损伤，完成了管道的结构完整性评定，从而实现了高温核一级复杂管系的蠕变-疲劳评估。

1 管道的应力状态解析解

依据叠加原理，管道的受力变形情况均可以简化为几种基本变形形式的组合。因此组合变形下管道内的应力可视为在压力P、三个方向力（Fx、Fy、Fz）和三个方向弯矩（Mx、My、Mz）共7种基本变形下管道内应力的叠加。本文作者在前期工作中已获得了对直管和弯管截面的应力状态解析解［5］。

直管截面外表面与内表面应力状态解析解见式（1）和（2）：

式中：D和d分别为管道的外直径和内直径；P为内压；α为截面任一节点（xp，yp）与x轴中心夹角；A为管道截面面积；Z1和Z2为截面模量，Z1=0.0982(D4-d4)/D，Z2=0.0982(D4-d4)/d。

弯管截面内表面、中间面和外表面的应力状态解析解分别见式（3）～（5），需要注意的是，该截面应力状态解析解仅使用于定义柔性系数λ≥0.2时的弯管结构（λ=Rt/(rˉ21- ν2)）。

式中：E为弹性模量；rˉ为平均半径；t为厚度；i1，i2，ψ，X1，X2，X3，X4，σintm，σinnb，σouttm，σoutnb为应力指数 ，详见ASME-NB-3650。

2 应力线性化及误差分析

2.1 应力分类及线性化

依照 ASME-ⅠⅠⅠ-5-HBB进行蠕变-疲劳评定时，需对应力分析结果进行应力分类及线性化。依据2017 版 ASME-ⅠⅠⅠ-Appendix-XⅠⅠⅠ-3110［6］规定 ，管道的薄膜应力应对整个管道截面进行平均，弯曲应力应与管道截面质心的距离成正比。通用有限元分析软件ANSYS并不能得到通过管道截面中心路径的应力分析及线性化结果，根据ASME规范，应力分析结果可以使用应力积分法进行处理，推导出的膜应力和弯曲应力张量的计算公式见式（6）～（7），将§1推导的应力张量解析解沿应力分类线（Stress Classification Lines，SCL）通过横截面进行积分，可以得到膜应力、弯曲和峰值应力分量。式中：σij，m为薄膜应力张量；σij，b为弯曲应力张量。

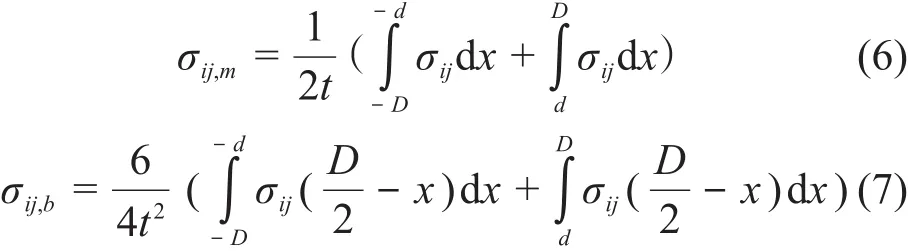
峰值应力张量由总应力分量减去薄膜应力及弯曲应力张量获得，管道壁面各位置的峰值应力张量计算公式见式（8）：

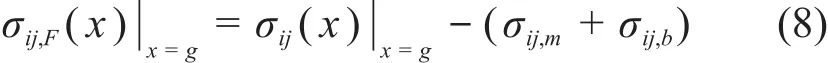
式中 ：σij，F( x)|x=g为管道壁面的峰值应力张量；σij( x)|x=g为管道壁面的总应力张量；g为管道截面上相应的厚度位置。

据此，依据弹性力学理论分别将上述计算所得的应力张量计算出三个主应力，并依据相应规范采用的应力强度理论计算出可供评定使用的薄膜应力、弯曲应力和峰值应力。

2.2 应力分类及线性化误差分析

为了验证应力线性化结果的正确性，本文建立了一个管道模型。该管道两端固定约束，内部承压0.45 MPa，管道温度700℃。对该模型分别采用三种计算方法进行分析：1）使用ANSYS建立管道实体模型进行有限元分析；2）提取ANSYS分析结果中截面处三个方向力和三个方向弯矩，采用应力状态解析解法进行截面应力计算；3）使用PepS管道软件进行应力分析，提取管道截面处三个方向力和三个方向弯矩，采用应力状态解析解法进行截面应力计算。管道模型及所选取的管道截面和局部坐标系见图1。

图1 管道模型及截面局部坐标系Fig.1 Geometry model and section local coordinate system of a typical pipe structure

管道模型所涉及的参数如下：外直径D=141.3 mm，厚度t=7.11 mm，弯转半径R=381 mm，平均横截面半径rˉ=67.10 mm，计算管道柔性系数λ=0.632＞0.2。管道材料为800H合金，假设材料各向同性，密度ρ=8 030 kg·m-3，泊松比v=0.31。700 ℃时的杨氏模量和热膨胀系数分别为156 GPa和14.3×10-6mm·mm-1·°C-1。

ANSYS实体单元分析结果显示：管道的最大应力为114.42 MPa，位于管道弯头处，管道的应力分布和最大应力处的截面应力见图2。

依据ANSYS和PepS两种软件分析结果提取最大应力弯管截面处的荷载（局部坐标系下），荷载见表1。将表1中截面荷载分别代入式（5）～（7）可以得到整个截面上（0°～360°）的管道的6个应力分量，然后根据最大剪应力理论计算相应的应力强度得到整个截面上的应力分布。图3和图4分别为使用ANSYS软件和PepS软件分析结果提取截面载荷计算出的管道截面应力，最大应力强度分别为120.95 MPa和122.28 MPa。相比ANSYS实体单元计算结果，管道截面应力分布趋势基本相同，且最大应力误差仅为5.7%和6.9%。结果表明：管道的应力状态解析解与有限元分析结果吻合良好。

图2 管道应力强度分布Fig.2 Stress intensity distribution of pipe

表1 弯管截面荷载Table 1 Elbow pipe sectional loadings

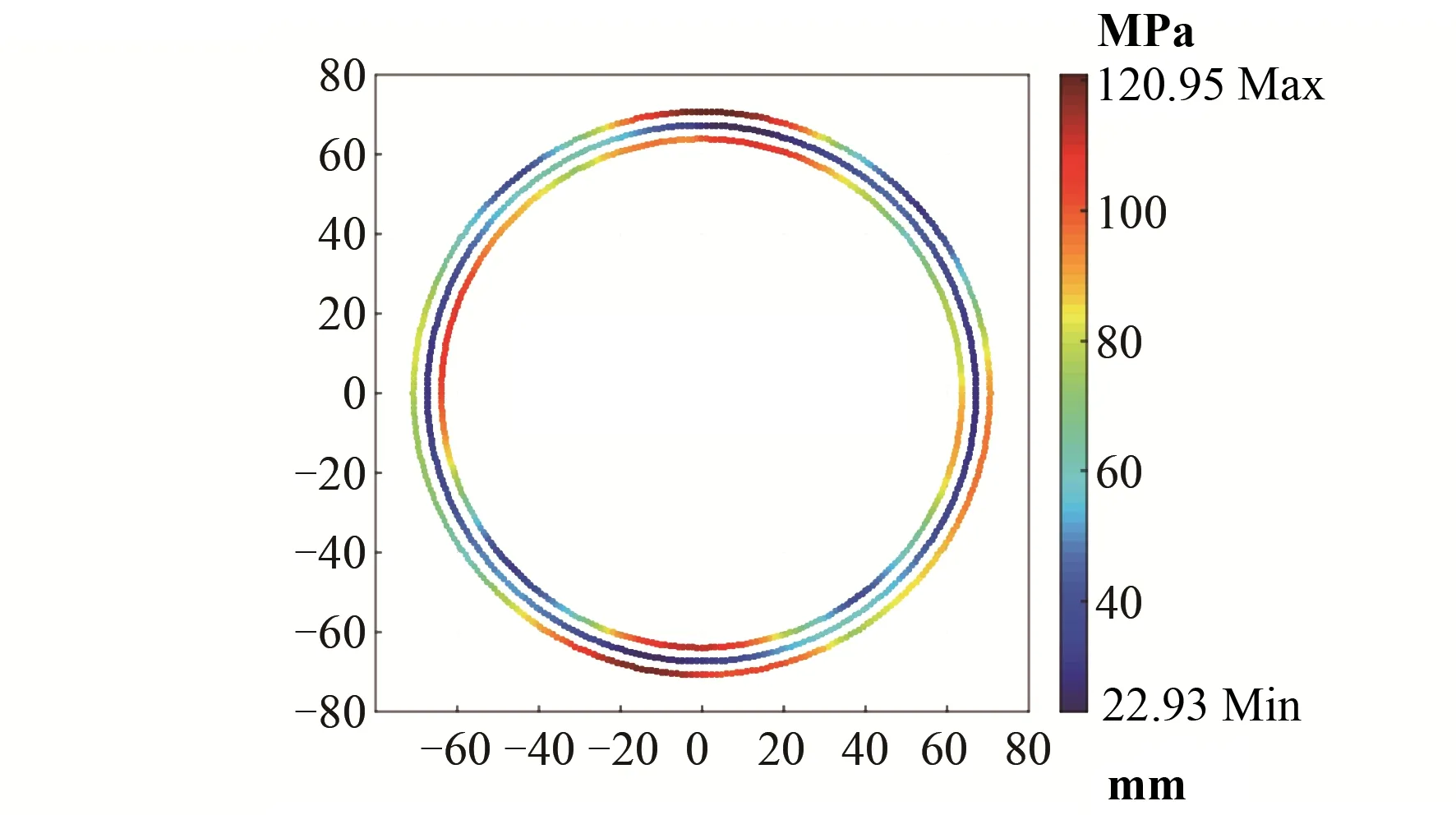
图3 采用ANSYS分析得到截面载荷计算的应力强度分布Fig.3 Stress intensity distribution calculated by cross section load which is obtained byANSYS analysis

管道截面的应力线性化需要使路径穿过管道整个截面，但使用实体单元进行有限元分析无法提供通过空白处的应力分类及线性化结果，因此仅对比使用ANSYS和PepS软件分析结果提取截面载荷计算出的管道截面应力线性化结果。基于上述计算结果，选取一条路径沿厚度方向通过整个管道截面并通过截面上应力最大点处，根据式（6）～（9）进行应力线性化，结果如表2所示。结果表明：薄膜应力与弯曲应力基本一致，但峰值应力略大。

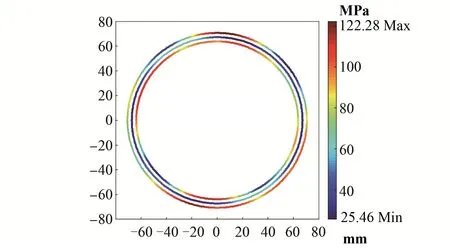
图4 采用PepS分析得到截面载荷计算的应力强度分布Fig.4 Stress intensity distribution calculated by cross section load which is obtained by PepS analysis

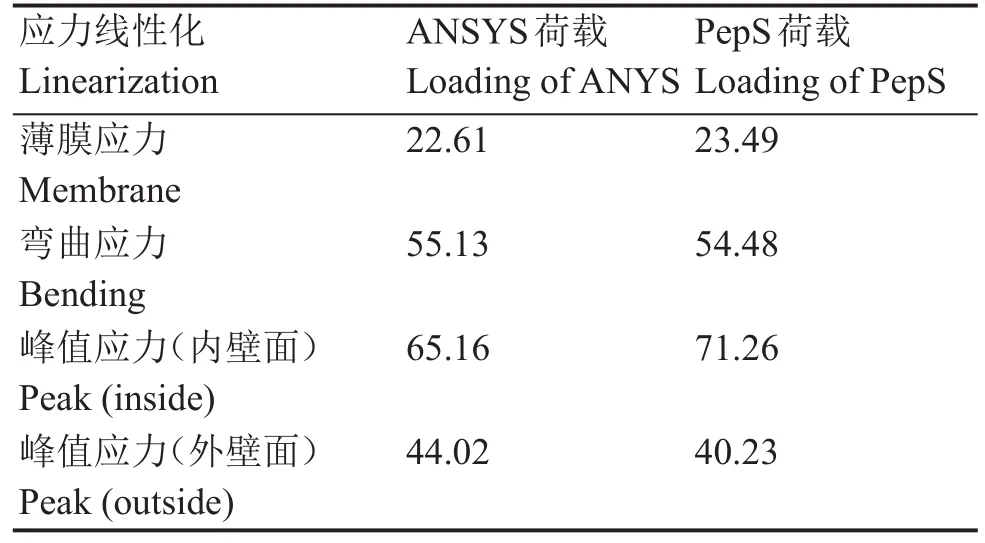
表2 弯管截面应力分类及线性化（MPa）Table 2 Linearization of stress intensity for stress classification

由上述计算和误差分析结果可知，现有的分析结果和应力分类线性化结果吻合较好。虽然PepS的结果中峰值应力的最大值偏大，更为保守，但对于大规模的复杂管道分析来说，采用该方法进行可大大减少计算时间，具有一定的实用性和可操作性。

3 TMSR-LF1回路管道蠕变-疲劳损伤评估

3.1 分析模型

TMSR-LF1回路是一种液态熔盐堆，其主容器为一体式结构［7-8］，内部除了有自身的反应装置外还包含了燃料盐回路的全部设备，如熔盐-熔盐换热器、燃料盐泵和燃料盐回路管道。TMSR-LF1回路的一、二回路设计温度分别为700℃和650℃，设计压力0.45 MPa。考虑回路温度高，管道热应力大的特点，在设计回路布局时，将冷却盐泵的支承设计为垂直方向固定，水平方向自由移动，并在水平方向设置阻尼支承。其余设备全部固定。回路总体布置如图5所示。

本文采用PepS软件对回路管道进行分析，依据ASME-ⅠⅠⅠ-5-HBB对管道进行结构完整性评价。分析时，建立管道模型，主设备简化为等效梁单元，其他部件以集中质量方式附加到梁单元上。TMSRLF1的分析模型如图6所示。

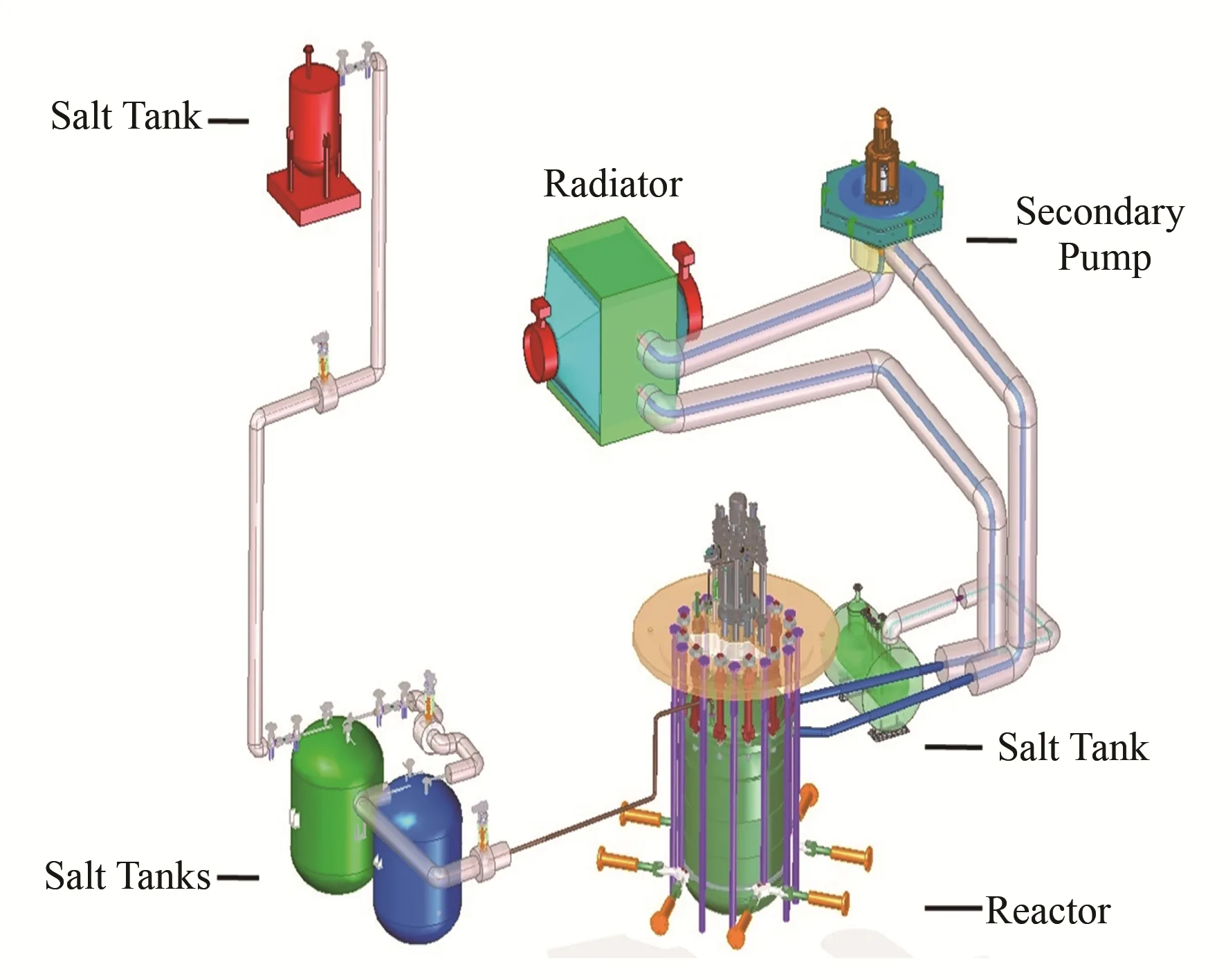
图5 TMSR-LF1回路布局示意图Fig.5 Layout diagram of the TMSR-LF1 primary loop

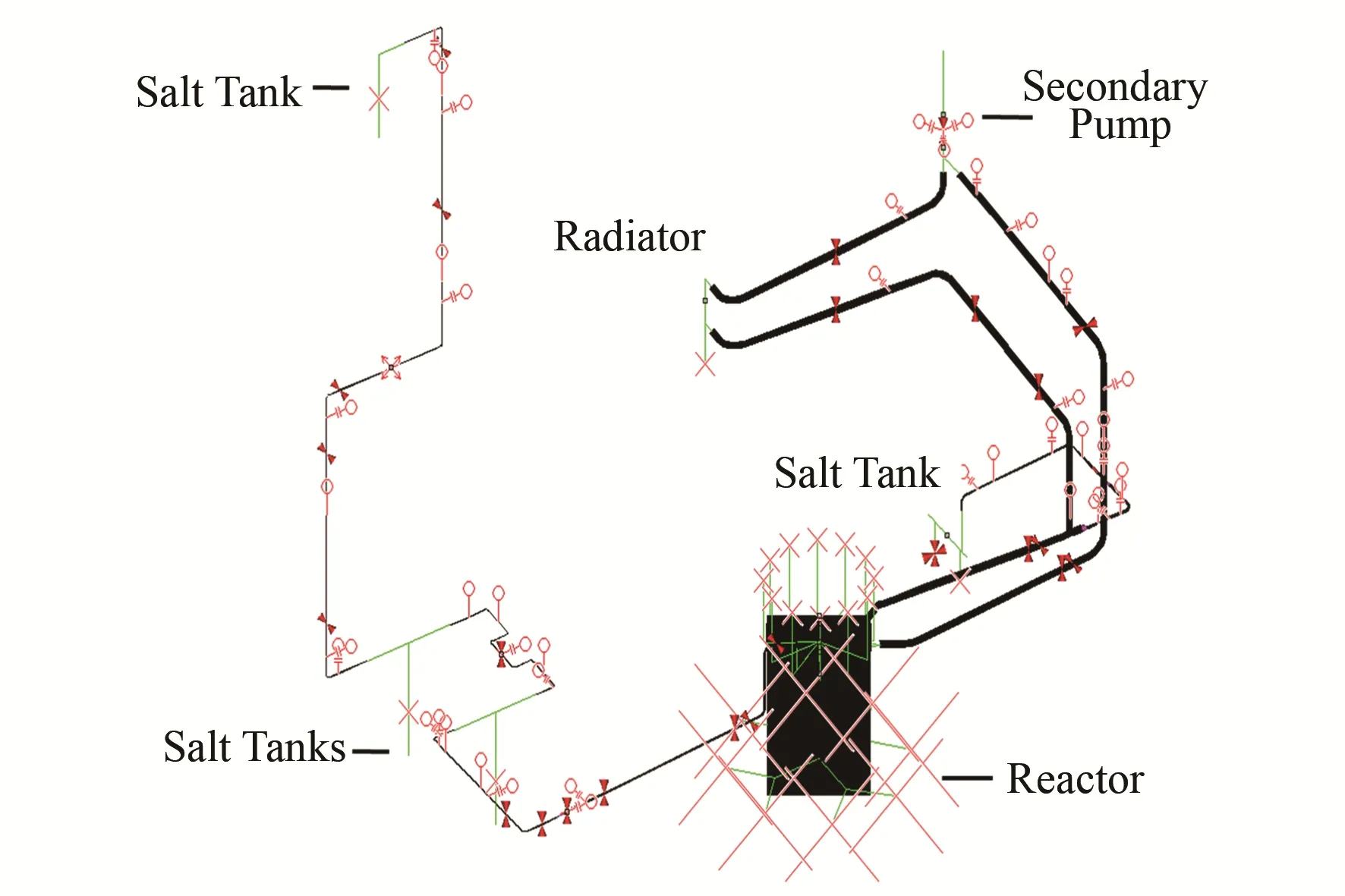
图6 TMSR-LF1回路分析模型Fig.6 Analysis model of TMSR-LF1 primary loop

3.2 应力分析结果

TMSR-LF1的所有管道均采用UNS N10003［9-11］合金制造，但由于材料数据的保密性，选用800H合金作为替代材料进行研究。主容器进出口温度分别为560℃和580℃，热量通过空气散热器向外散发。管道的结构参数和伴热保温材料重量见表3。本文分析了设计工况、A级工况，工况载荷设置见表4。在A级工况下，假设管道温度恒定。对于设计条件和A级服务的最大应力结果分析可以直接从PepS获得，如表4所示。

由于蠕变-疲劳损伤评定时需要进行应力分类及线性化，因此根据最大应力分布选择两条路径进行蠕变-疲劳损伤评估。路径的主要参数及截面类型见表 5，不同荷载组合下的截面荷载（Fx、Fy、Fz、Mx、My、Mz）见表6。根据上文所述方法计算了两条路径的应力并进行应力分类及线性化，计算结果见表7。

表3 管道的主要参数Table 3 Main parameters of pipes

表4 载荷及工况Table 4 Loading and conditions

表5 路径的主要参数Table 5 Main parameters of the target paths

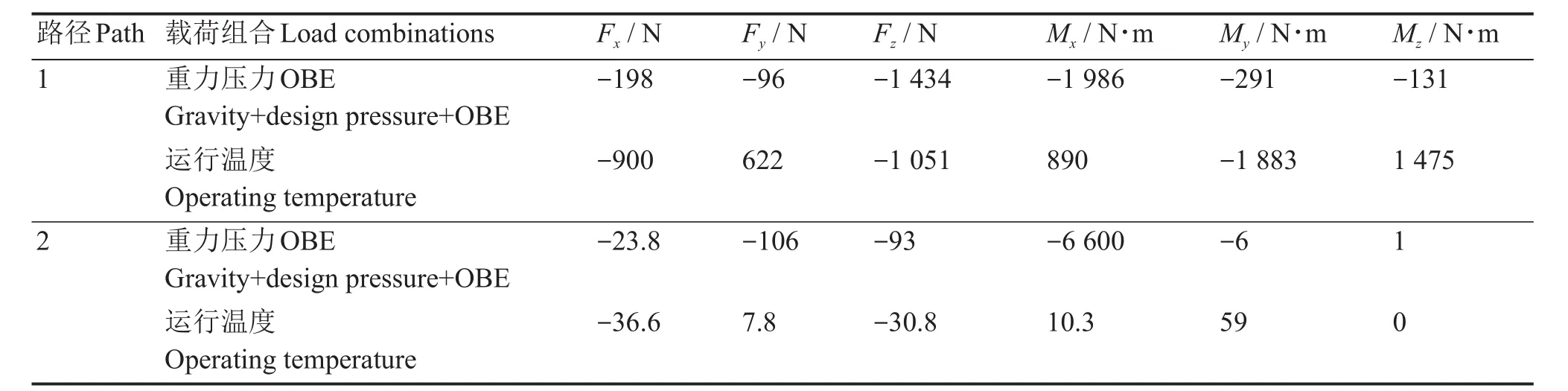
表6 不同载荷组合下的截面荷载Table 6 Sectional loadings under different load combinations

表7 应力分析及线性化结果Table 7 The results of stress linearization(MPa)

3.3 结构完整性评定

TMSR-LF1运行的一个温度循环包括预热、启停堆、运行等。TMSR-LF1回路的设计寿命为10年，运行次数80次，单次循环时间为1 000 h。

1） 应力应变变形限值评定

载荷控制的应力及应变变形限值评定依据ASME-ⅠⅠⅠ-NB-3650和ⅠⅠⅠ-5-HBB-T-1325进行。评价结果见表8。可以看出，其结果满足荷载控制的应力和应变限值极限要求。

2） 蠕变-疲劳损伤评定

依据 ASME-ⅠⅠⅠ-5-HBB-T-1400，疲劳蠕变损伤应满足式（9）：

表8 应力应变变形限值评定Table 8 Load controlled stress and strain evaluation

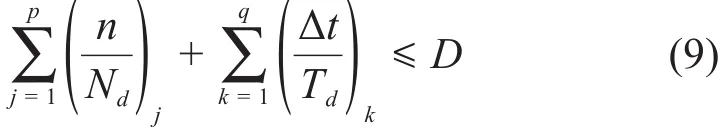
式中：D为总蠕变-疲劳损伤；其余系数详见ASME-ⅠⅠⅠ-5-HBB。

在一个循环过程中，总应变范围ɛc可以由式（10）计算得出：

式中：ɛt为总应变损伤；Δɛmod为修正的最大等效应变范围；Δɛc为蠕变应变增量；Kv为多轴塑性和泊松比调整系数；K为应力集中因子。

依据ASME-ⅠⅠⅠ-5-HBB-T-1400规范，路径1和路径2的蠕变损伤和疲劳损伤计算结果见表9。结果显示：累积疲劳损伤仅为0.000 1，可忽略不计。总的损伤结果∑（n/Nd）+∑（Δt/Td）没有超过材料的蠕变-疲劳包络线，因此，本文分析的管道满足蠕变疲劳极限的要求。

表9 蠕变-疲劳损伤评定结果(MPa)Table 9 Results of creep-fatigue damage evaluation

4 结语

为解决复杂核安全一级高温管道系统结构分析与评定的工程问题，本文首先给出了管道构件截面（直管和弯管或弯头）在各种载荷组合下的应力张量解析式，随后计算对管道截面应力分量和相应的应力线性化结果，并成功地与有限元分析结果进行对比，得到了良好的拟合效果。最后，利用PepS软件对TMSR-LF1回路管道进行了力学分析和结构完整性评估。该研究工作将管道分析软件与ASME-ⅠⅠⅠ-5-HBB评定规范进行了有效衔接，明确了蠕变-疲劳评定方法，实现了核安全一级高温复杂管系的高效计算分析与结构完整性评估，并为管道软件的高温评定规范开发提供了理论基础，对高温反应堆管道设计具有重要的理论和工程实践意义。