液态金属中固态颗粒物运动特性的数值模拟

刘 鹏 杜晓超 洪 锋 袁显宝

（三峡大学机械与动力学院 宜昌 443002）

液态铅铋共晶合金（Liquid Lead-Bismuth alloy，LBE）具有良好的中子学性能、抗辐射性能、热物性和传热性能，是第4代反应堆以及加速器驱动次临界 系 统（Accelerator Driven Sub-critical System，ADS）的散裂靶兼冷却剂［1-2］。铅铋合金冷却剂跟其他流体一样，会对其流经的冷却剂通道产生腐蚀冲刷、FAC效应等［3-4］，使其结构材料腐蚀脱落形成颗粒；另外，铅铋合金中不可避免地会存在一些杂质，其中一些熔点比铅铋合金高的杂质不能熔化，就会形成颗粒随铅铋合金在回路中流动；综合上面这两种情况，若这些颗粒沉积在管壁时，不仅影响铅铋合金的流动，而且还会影响传热，造成管道局部温度升高，这会造成极大的安全隐患。另外，铅铋合金开展实验困难［5］，模拟不失为一种好的方法。华北电力大学的周涛等［6］对亚微米颗粒在Sierpinski海绵模型中热泳沉积做了研究；刘亮等［7］对铅铋合金中颗粒物的沉积做了研究，并且设计了一种防铅铋合金中颗粒物沉积的管道；杨旭等［8］对矩形通道内不溶性腐蚀产物的沉积分布进行了研究；陈娟等［9］对纳米颗粒在液态金属内的热泳规律进行了研究等。但是这些颗粒最终还是存在于管路中，考虑到颗粒的密度均小于液态铅铋合金的密度，因而考虑基于密度差，研究颗粒在液态铅铋合金中的上浮规律，这对于颗粒的除去研究是很有意义的。

1 物理模型

标准k-ε湍流模型是目前工程计算中应用最为广泛的模型，可以满足大部分仿真需要，所以模拟过程选用标准k-ε湍流模型作为计算模型。k和ε的方程分别为：

其中：pk为湍动能k的生成项，由下式确定：

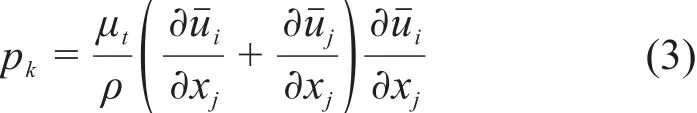
式中：μt= ρCμk2/ε；Cμ、σk、σε、C1ε和C2ε为湍流模型系数，根据Rodi建议的标准值分别取：Cμ=0.09，σk=1.0，σε=1.3，C1ε=1.44，C2ε=1.92［10］；且本文Fluent模拟计算采用此值。

本研究不考虑相间的质量和热量传递，连续相的欧拉控制方程为：

连续性方程：

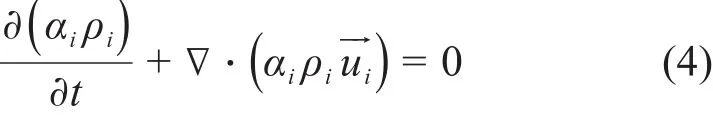
式中：α、ρ、u分别表示体积分数、密度和速度，下标i表示液相。

动量守恒方程：

式中：p、μ、g、F分别表示压力、动力粘度、重力加速度以及相间作用力。

颗粒在流场中的运动轨迹是其在流场中所受的各种作用力共同作用的结果，在DPM离散相模型中，流场中颗粒的运动轨迹是通过对拉氏坐标系下的颗粒作用力微分方程进行积分得到的，颗粒的作用力平衡方程为：

式中：FD(u-up)是单位颗粒质量所受到的流体曳力；Fx为其他作用力，包括浮力、阻力、压力梯度力、附加质量力、Basset力、Saffman力和Magnus力等；其中竖直方向主要的力是重力、浮力和阻力，在运动初始阶段压力梯度力和附加质量力也较为重要；在径向方向（以下称x方向）主要的力是Saffman力，在不考虑颗粒自身的转动时Magnus力可以忽略。由于颗粒物的粒径为微米级，因而不考虑布朗力和热泳力等。其中：

式中：u为流体速度；up为颗粒速度；μ为流体动力粘度；ρ为流体的密度；ρp为颗粒的密度；dp为颗粒直径；CD为曳力系数；Rep为相对雷诺数，定义为：

其中：曳力系数CD可由式（9）计算得到［11］：

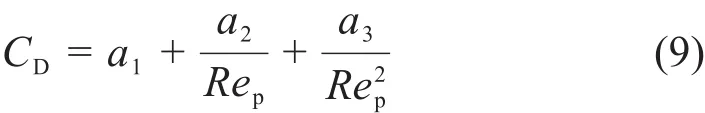
式中：a1、a2、a3为常数。具体取值见表1。

表1 不同雷诺数下a取值Table 1 Value of a under different Reynolds numbers

2 研究对象与方法

为了确定颗粒上浮之后的粒径分布与浓度分布范围，计算颗粒的起始位置与终点位置在x方向的偏移量，以此偏移量的长度为半径的圆形范围即为颗粒最大概率的分布范围。由于容器是轴对称的圆柱形，为了更好的理解这一问题以及定量得到计算结果，同时也为了减少计算量和增加收敛性，所以将三维的模型降维成二维，如图1所示，参考华北电力大学在液态铅铋合金氧控实验中所用的装置［1］，设置尺寸为直径L=400 mm，高为H=500 mm；网格划分采用结构化网格。但是在后面进行颗粒分布的模拟时，为了便于观察模拟计算结果，采用三维模型，并且使用结构化网格进行计算，经网格无关化验证，二维网格数量为5万左右，三维网格为60万左右，截面的网格情况如图2所示。

表2 液态LBE物性参数经验关系式Table 2 Empirical relationship of liquid LBE physical parameters

由于Fluent自带的数据库没有铅铋合金，所以需要在Fluent中创建新的材料的物性数据库，根据Koji等［12］、苏子威等［13］的研究结果［14-15］，计算用的铅铋合金的物性参数列于表2中。代数方程的求解全部采用SⅠMPLE算法，方程的求解差分方式采用标准差分方式，湍流动能k、以及动量和能量等均采用二阶迎风差分格式，这种格式使得计算的速度较快，同时又具有较好的精度和收敛性；选择双向耦合方式，即颗粒物能影响流场，同时流场的参数变化又会反过来对颗粒物的运动产生影响，颗粒物选择为氢化锂与氧的反应产物氧化锂（Li2O），为了比较全面的研究粒径对氧化锂颗粒物运动规律的影响，粒径选择为0.1～1.0 mm［16］，壁面设置为吸收面。

图1 几何模型Fig.1 Geometric model

图2 截面网格Fig.2 Section grid

3 模拟结果与分析

3.1 粒径的分布

当铅铋合金的温度为573.15 K时，不同直径的颗粒在流场相同的位置，以相同的初始条件进行计算得到的结果如图3所示，由图3可知，在同一温度下，不同直径的颗粒，在x方向的速度随时间的变化趋势相同，首先在第一阶段，速度在短时间内达到最大值，斜率较大；接着进入第二阶段，速度快速下降，达到平稳的阶段，随着上浮到容器的顶端，计算结束，速度变为0；在第一阶段时，浮力大于重力以及流体的阻力和附加质量力的总和，所以向上做加速运动，出现x方向的位移是由于x方向存在萨夫曼升力的作用，大小与颗粒运动速度的平方成正比，方向为垂直于颗粒运动方向。随着颗粒进入第二阶段，上浮速度的降低，萨夫曼升力减小，所以x方向的速度也减小。

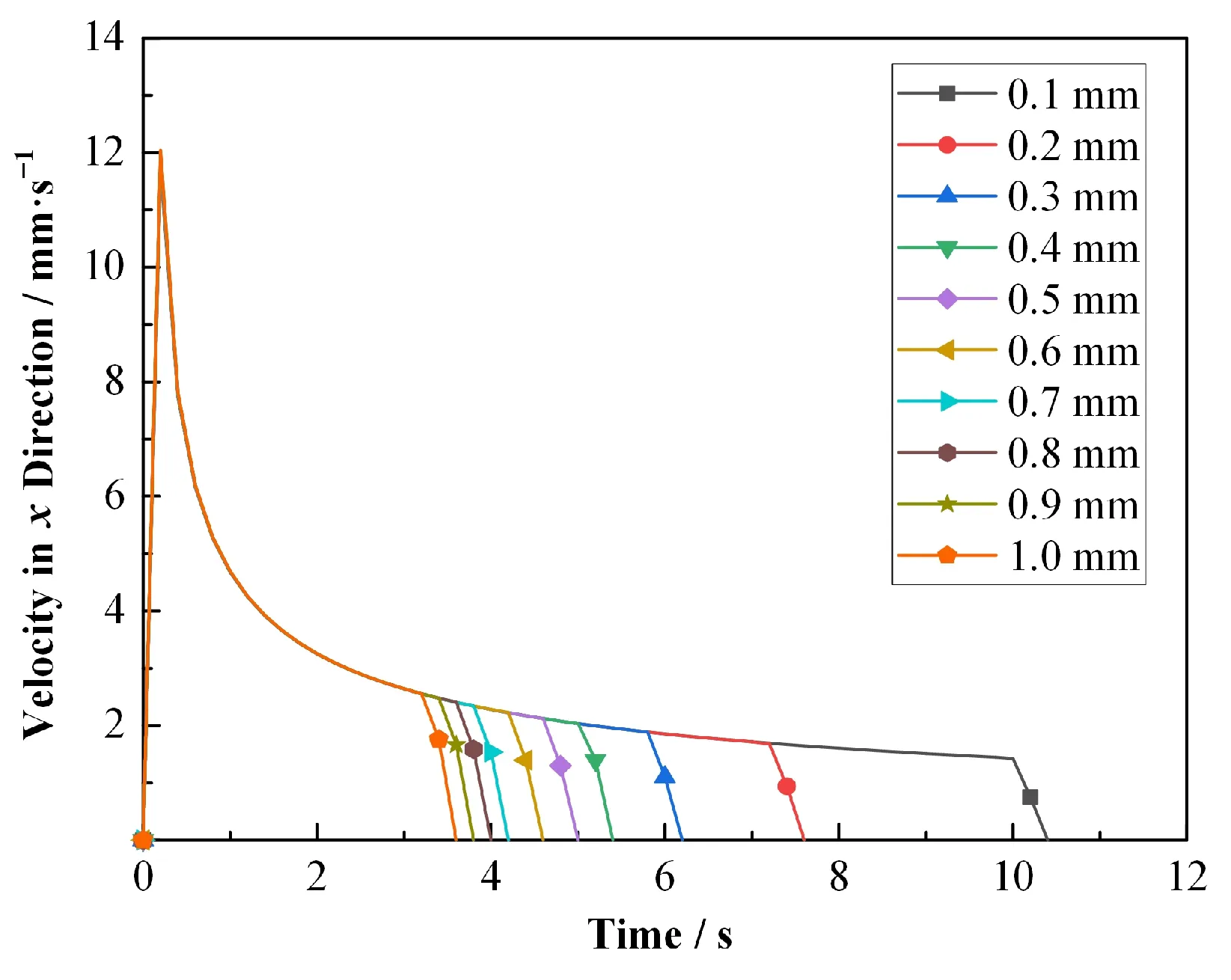
图3 颗粒物在x方向的速度随时间的变化Fig.3 Ⅴelocity of particles in the x direction with time

由图4结合图3可知，图3的第一阶段对应于图4的初始直线段，斜率较大，因而速度较大；直线段后为曲线段，斜率减小，对应图3的速度减小的第二阶段，由于在同一温度下，颗粒在x方向的速度随时间变化的趋势相同，所以，位移随时间变化的趋势也相同。从图4也可以得出颗粒在x方向位移的范围，介于20～35 mm。

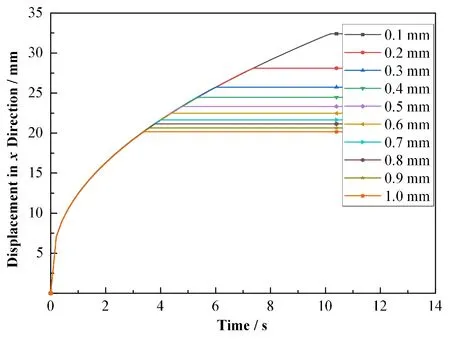
图4 颗粒物在x方向的位移随时间的变化Fig.4 Displacement of particles in the x direction with time

图5 为同一颗粒物直径，在不同的温度下，x方向的速度随时间的变化，与图3的趋势是一致的；由图5可知，在不同温度的铅铋合金里，颗粒物在x方向的速度大小不同，相差不超过2 mm，但是趋势相同，造成这种现象的原因是不同的温度导致铅铋合金的密度和粘度不同，这些参数又会影响浮力与阻力以及附加质量力的大小，从而颗粒物的上浮速度发生变化，导致萨夫曼升力大小发生变化。出现如图5所示的不同温度下颗粒物的x方向速度的不同。

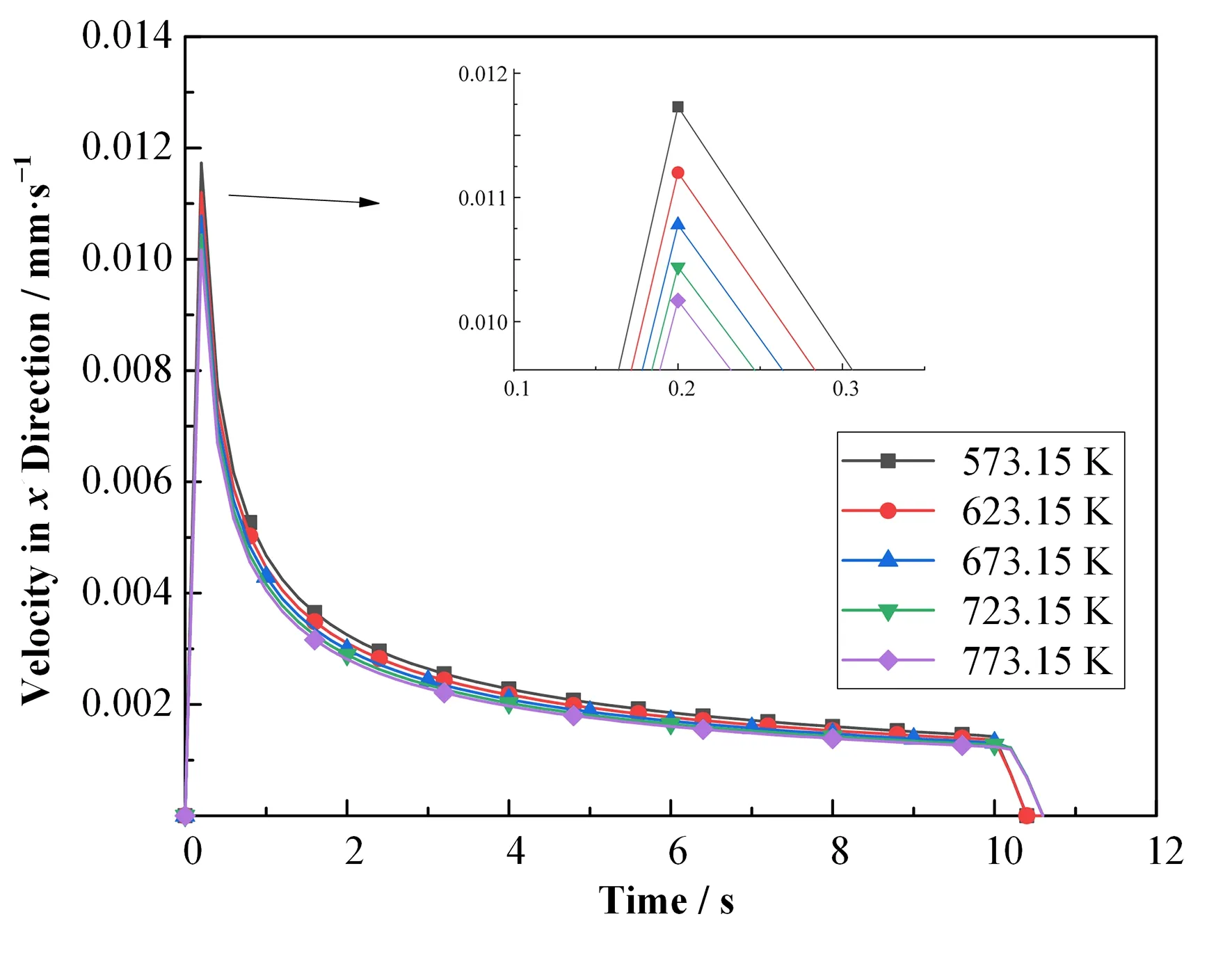
图5 颗粒物在x方向的速度随时间的变化Fig.5 Ⅴelocity of particles in the x direction with time

图6 为同一颗粒物直径，在不同的温度下，x方向的位移随时间的变化，与图4趋势一致；不同的温度会导致铅铋合金的密度、粘度不同，这些参数进而影响浮力与阻力以及附加质量力的大小，导致x方向的萨夫曼升力的大小发生变化；由图6可知，随着温度的升高，x方向的速度降低，速度的降低导致在x方向的位移也减小，于是出现图6所示的情形。

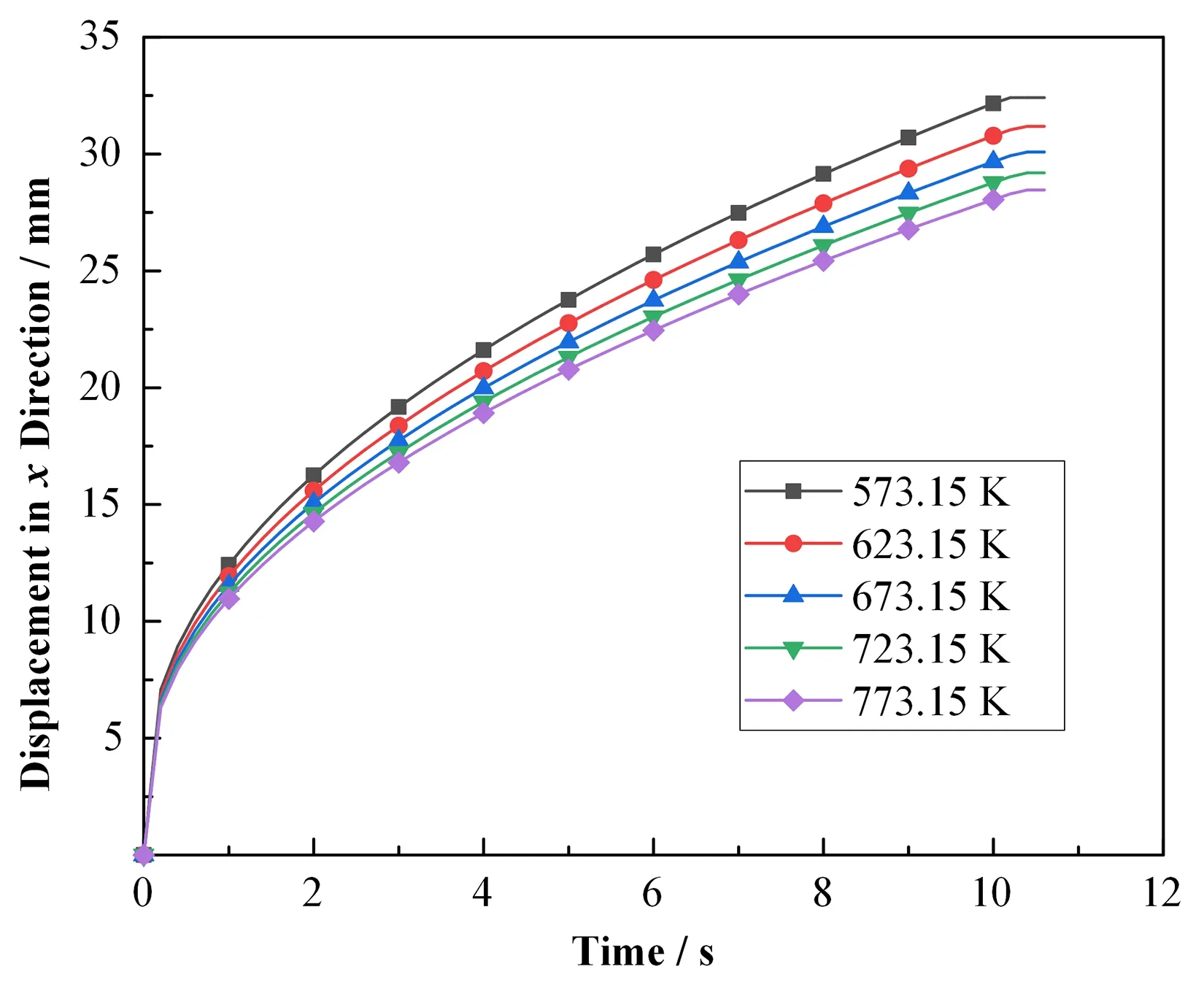
图6 颗粒物在x方向位移随时间的变化Fig.6 Displacement of particles in the x direction with time

图7 是粒径与x方向最大位移的关系，在同一温度下，x方向的最大位移随颗粒物直径的增大而减小；造成这一现象的原因从物理模型分析，随着颗粒直径的增大，浮力的增加量要大于重力的增加量和阻力的增加量，由前面的分析可知，颗粒的加速时间非常短暂，所以附加力的作用时间较短，这就导致颗粒在y方向的合力较大，因而上浮速度更快，在x方向的萨夫曼升力与阻力都与速度的平方成正比，升力系数对升力的大小影响能力有限，所以x方向的速度变化很小，这一点与图3所示的一致，因而在上浮时间减小的情况下，x方向的位移也减小。另一方面，温度对x方向最大位移的影响是通过影响流体的密度、粘度等物性来间接影响颗粒物的分布。通过图7分析也可知，直径大的颗粒物分布的靠近轴线，直径小的颗粒物则较远离轴线。

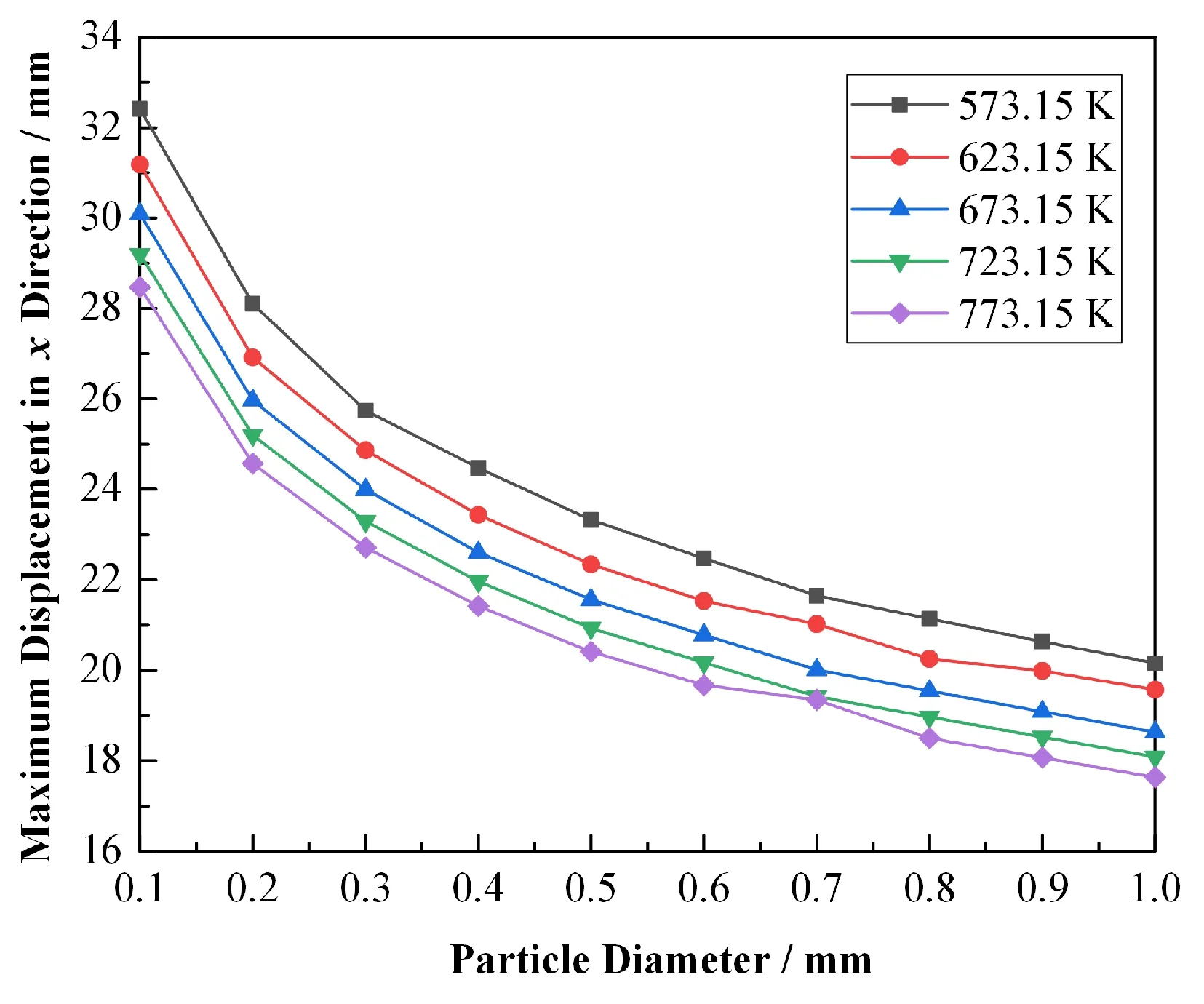
图7 颗粒物x方向最大位移随颗粒物直径的变化Fig.7 The maximum displacement of the particles in the x direction varies with the diameter of the particles

3.2 时间的分布

图8 显示颗粒的上浮时间随颗粒物的直径的变化关系，随着颗粒物直径的增大，上浮时间减小，这与对图7的分析是一致的，是由于直径的改变导致各种力的变化，进而影响所作用的对象-颗粒，可以发现上浮时间的差距还是很大的；但是流体的温度对上浮时间的影响很小，尤其是对小直径的颗粒而言，几乎没有影响，当直径大于0.5 mm时，出现了一定的的差别，但差距也没有超过0.5 s。

图8 上浮时间随颗粒物直径的变化Fig.8 The floating time varies with the diameter of the particles

3.3 浓度的分布

图9 为三维模型的情况，在初始时刻容器内的颗粒物的分布俯视图，由于液态铅铋合金不透明，实验测定颗粒物分布有困难，因而颗粒物的坐标暂时采用均匀分布随机生成数法由Matlab随机生成。

图9 初始颗粒分布俯视图Fig.9 Top view of the initial particle distribution

图10 显示了颗粒物浓度的分布，可以发现颗粒近似成对称分布；同时，围绕中心轴Position=0 mm，以s=90 mm为半径的范围内，颗粒物的浓度要比其他位置平均高2～3倍。

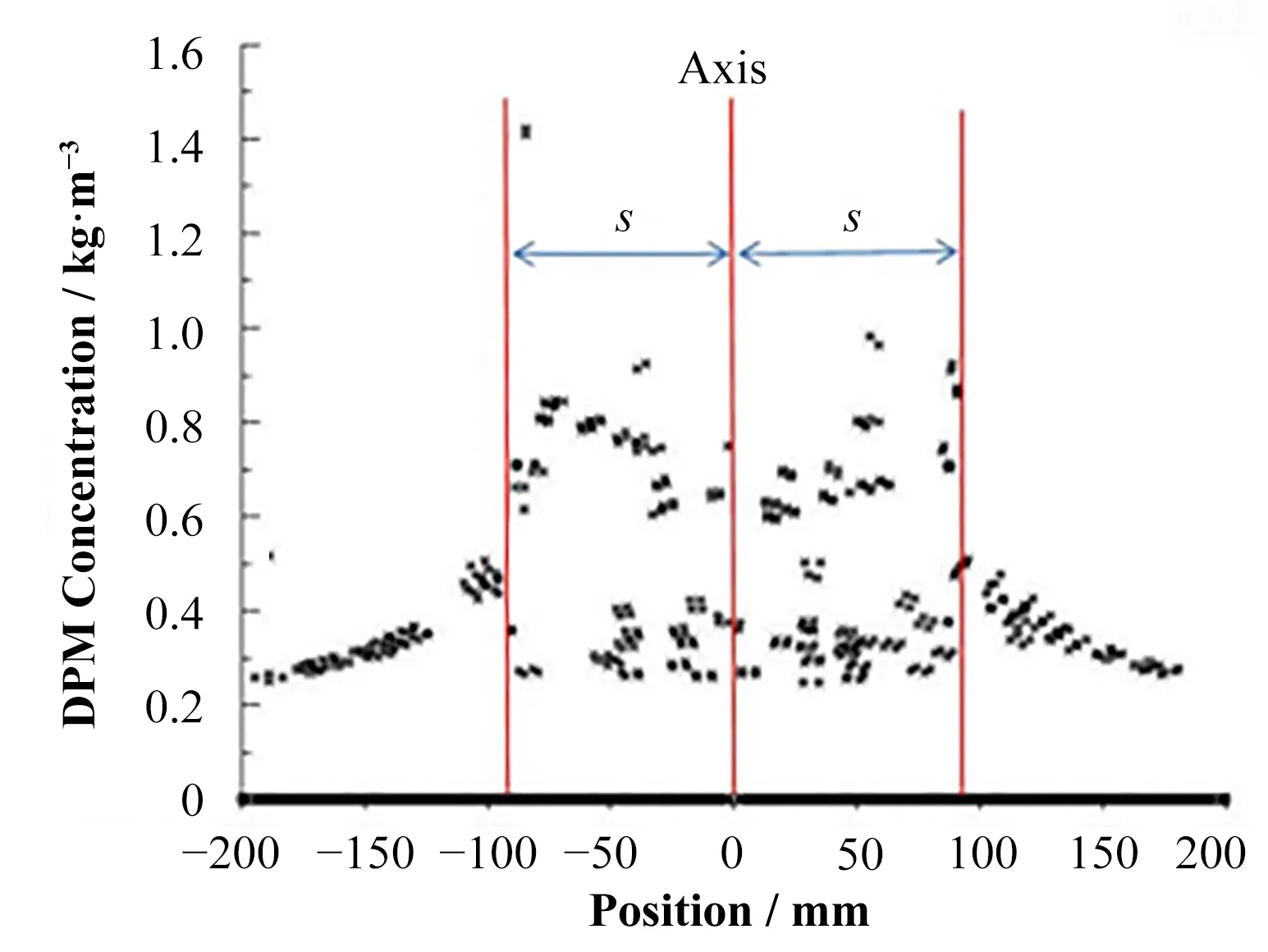
图10 颗粒物浓度分布Fig.10 Particle concentration distribution

4 结语

1）在同一温度下，直径大的颗粒物上浮时间短，直径小的颗粒物上浮时间长，且温度对上浮时间的影响较小，可以忽略；颗粒物的直径与其在x方向的最大位移成负相关，即直径大的颗粒物在x方向的位移小，直径小的颗粒物在x方向的位移大。

2）在同一颗粒物直径下，温度与颗粒物在x方向的最大位移成负相关，即温度高时x方向的位移小，温度低时x方向的位移大。

3）直径大的颗粒物分布靠近圆柱轴心位置，直径小的颗粒物分布相较直径大的颗粒物分布远离轴心位置。

4）总的来说，围绕轴心半径为90 mm左右的圆内，颗粒物的浓度较其位置要高2～3倍，因此，在对铅铋合金进行净化时应着重关注这一范围，净化的效率与效果较好。