超声金属焊接双法兰结构声学系统设计

靳 涛，陆平山，胡 扩，于保华，胡小平

（ 1. 杭州电子科技大学机械工程学院，浙江杭州310018；2. 浙江日发航空数字装备有限责任公司，浙江绍兴312500 ）

由于超声波金属焊接具备焊接速度快、 能耗低、环保等优点，故其应用范围较广，如应用于电容器或硅半导体的连线焊接、 手机电池电极焊接、电器中的金属片和电极焊接、食品机械中的洁净容器焊接等[1-2]。 超声波金属焊接的机理是在施加径向静压力的情况下，将超声频振动传递到两个需要焊接的金属表面，使两个焊件表面相互摩擦而产生分子层之间的相互扩散并连接在一起。

超声波焊接系统主要由超声波发生器、 换能器、变幅杆和焊接工具头组成。 在焊接时，通过给焊接工具头施加径向静压力，向焊件传递超声振动能量。静压力通常为200～600 N，因此需要声学系统安装的法兰具有足够的强度来保证结构刚度[3]。 此外，安装法兰的位置和尺寸参数直接影响声学系统超声波传递效率和结构刚度，影响超声焊接性能。

目前，在超声金属焊接声学系统的安装方法研究中， 通常选用变幅杆的声学节点作为固定点，即在变幅杆振幅为零的位置安装法兰盘[4-6]（图1a）。由于焊接头需承载较大的径向静压力，单支撑的节点法兰处的应力易超过其材料强度，变幅杆结构会发生破坏。 同时，理论上说的节点位置是某一特定位置，而在实际加工中因加工误差、频率漂移等问题易发生偏差，导致设计的法兰不再设置于振幅为零的位置，这足以严重影响振幅输出。 可见这种单法兰的结构设计，实际上难以满足超声传递效率高和结构刚度强的双重要求。

如图1b 所示， 针对传统单法兰支承结构存在的问题，本文提出了一种声学系统双法兰支承的结构设计方案， 并通过Ansys 数值仿真和单因素实验相结合的方法，获取了法兰厚度对超声传递效率和支承结构刚度的影响规律，优化了整体声学系统的超声传递效率和结构刚度，还通过仿真分析和测试实验验证了双法兰结构的有效性，为超声金属焊接声学组件设计提供了新思路。

1 超声焊接声学组件整体结构设计

本文设计的双法兰结构超声焊接声学组件的整体结构， 其系统频率为40 kHz、 变幅杆材料为6061 铝合金、焊接工具头采用45 钢制成。考虑加工的简易性及声学系统的结构刚度，该设计在传统变幅杆的基础上取消了声学节点安装法兰的方式，在变幅杆上下端各增加了薄片状的法兰盘，用于声学系统的安装固定，增加结构刚度的同时保证超声的传递效率。 该结构的工作模式为：换能器产生的超声频机械振动传递到变幅杆， 由变幅杆将振幅放大，再传递到焊接工具头上进行焊接工作。

2 超声焊接声学组件支承法兰设计

2.1 法兰材料、结构和直径的设计

2.1.1 法兰材料

首先，超声波在传递过程中，必须保证传递介质的阻抗特性相近或一致，否则会导致一部分超声波发生反射，影响超声波的传递[8]。 在双法兰结构声学组件设计中，变幅杆材料为铝合金、焊接工具头采用45 钢， 而法兰作为变幅杆与焊接工具头之间的连接件，其材料应在铝合金和45 钢中选择，以保证超声波的良好传递。

其次，焊接工具头在工作时将承受较大的径向静压力，而法兰作为声学系统的支承组件，其材料应具有足够抗拉强度来承载该静压力，以保证声学系统结构刚度，且法兰在超声振动过程中将产生高频振动，为保证其使用寿命，需有足够的抗疲劳强度。 由于45 钢材料的抗拉强度和抗疲劳强度均远优于铝合金， 综合考虑结构刚度和使用寿命的要求，最终选择45 钢作为法兰结构的制作材料。

2.1.2 法兰结构和直径

在声学系统振动过程中，应尽量避免将能量传递到安装座， 否则会造成能量损耗并影响声学传递，甚至对机架结构造成破坏[7]。 因此，针对法兰的结构设计，要求在保证其具有足够抗拉强度和抗疲劳强度的同时， 尽量减小其对超声波传输的阻碍，从而降低超声波能量的损耗。 在超声波传递时，法兰的内部随着声波高频振动， 外部与机架相连固定，而内外相连的位置会发生较大变形，造成较多的超声波能量损耗。 本文设计的法兰，其中间设有圆形大孔， 作为上下两段声学组件的连接螺栓孔；外围设有圆形小孔，作为声学系统与机架连接的安装孔，通过螺栓安装在圆管型固定座上；法兰在连接螺栓孔与法兰安装孔之间为弧形槽口（图2），槽口的圆弧顶部会形成应力集中点，将原来分散的应力集中起来，使法兰在产生较大形变的同时减少能量的损耗。 考虑到声学系统整体的结构紧凑性及在超声焊接设备上的安装需求，本文设定法兰直径为41 mm、连接螺栓孔直径为12.7 mm、法兰安装孔直径为3.2 mm。

2.2 法兰厚度的设计和优化

法兰的厚度对超声波传输效率及声学系统结构刚度影响显著，厚了会阻碍超声波传输，薄了会降低结构刚度。 同时考虑刚度和传输效率，本文采用Ansys 数值仿真分析法对法兰厚度进行优化设计，限定变幅杆和焊接工具头的尺寸，既能保证超声波传递效率、又能保证结构刚度，并对不同法兰厚度的声学组件进行静力学分析、模态分析和谐响应分析，进而设定法兰厚度的参考值。 限定取值范围见表1。

2.2.1 静力学分析

本文对不同法兰厚度的声学组件进行静力学有限元分析， 建立如图3 所示的Ansys Workbench分析模型，对法兰配合面施加固定约束，给焊接工具头端部施加500 N 径向压力，分析不同厚度法兰的应力情况和变形情况。图4 是法兰厚度为0.4 mm的声学组件静力学分析应力云图。

由表2 所示不同法兰厚度的声学组件有限元分析结果可知：在相同载荷条件下，法兰越薄，声学组件的最大等效应力和结构变形量越大，且变形量与最大等效应力基本呈正比； 法兰厚度为0.4 mm的声学组件， 其最大等效应力达到333.79 MPa，这接近45 钢的屈服强度（355 MPa），几近失效。

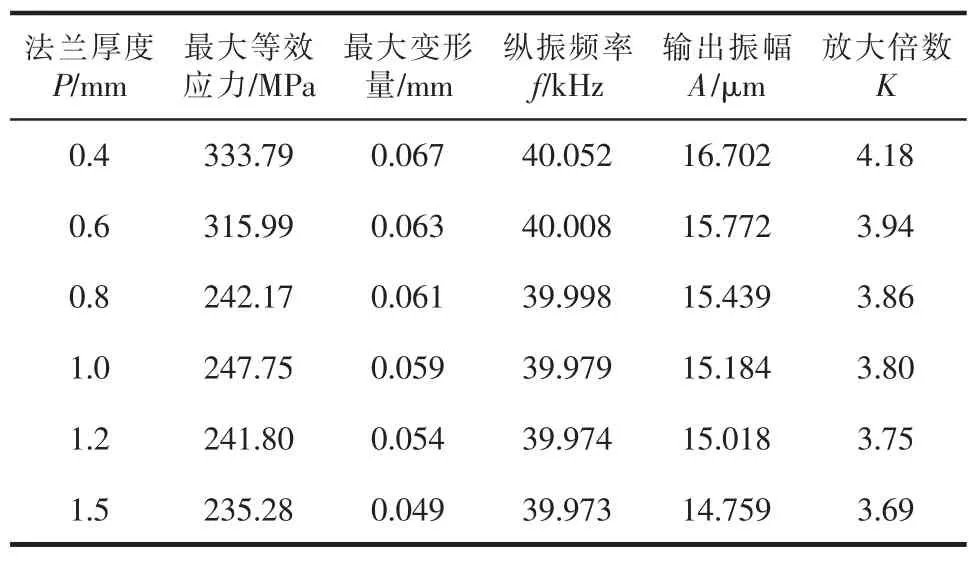
表2 不同法兰厚度声学组件有限元分析

2.2.2 模态分析

本文建立了Ansys Workbench 分析模型， 在法兰配合面施加固定约束，并在39～41 kHz 的频率范围内对不同法兰厚度的声学组件进行模态分析。 图5 是法兰厚度为0.4 mm 时的声学组件模态分析纵振变形云图。 不同法兰厚度声学组件的纵振频率变化情况见表2。

2.2.3 谐响应分析

本文在模态分析的基础上， 选用了Harmonic Response 模块对变幅杆进行谐响应分析，在变幅杆大端X、Y平面施加4 μm 的位移载荷，测量纵振模态下焊接工具头末端面的轴向最大位移，并计算其放大倍数。谐响应分析结果见表2。图6 是法兰厚度为0.4 mm 的声学组件受到激励后在工具头末端产生的轴向位移图。 可见， 声学组件的纵振频率为40.052 kHz 时的振幅为16.702 μm， 声学组件对换能器输出振幅的放大倍数为4.2 倍。

2.2.4 法兰厚度的选择

本文以变幅杆的振幅放大倍数表征传递效率，以最大等效应力表征结构刚度，基于有限元分析结果可优化获取合适的法兰厚度，从而获得较好的超声波传递效率和结构刚度。 图7 是焊接工具头在受静压力为500 N 负载时的声学组件最大等效应力、最大变形量及声学系统振幅放大倍数与法兰厚度的关系曲线图。

从图7 可看出：

（1）法兰厚度从0.4～1.0 mm 时，声学组件的最大等效应力大幅降低， 且法兰厚度在0.8 mm 处达到较低值；法兰厚度从1.0～1.5 mm 时，声学组件的最大等效应力降低程度并不明显。

（2）法兰厚度从0.4～0.8 mm 时，声学组件振幅放大倍数减少较明显，而法兰厚度大于0.8 mm 时，其振幅放大倍数变化相较于前一区间更平缓。

（3）声学组件的最大变形量与法兰厚度基本呈反比，即法兰越厚、变形量越小。

综上可知，法兰厚度约为0.8 mm 时，声学组件具有较低的最大等效应力，其形变量较小，也有足够的结构刚度， 同时具有较大的振幅放大倍数，表现出良好的超声波传递效率。 因此，本文确定法兰厚度为0.8 mm。

3 超声焊接声学组件优化设计与结果分析

3.1 双法兰声学组件优化设计

选定法兰厚度为0.8 mm 的声学组件， 对双法兰声学组件进行整体优化，以降低变幅杆的最大等效应力和提高振幅放大倍数为优化目标函数，所得优化结果见表3。

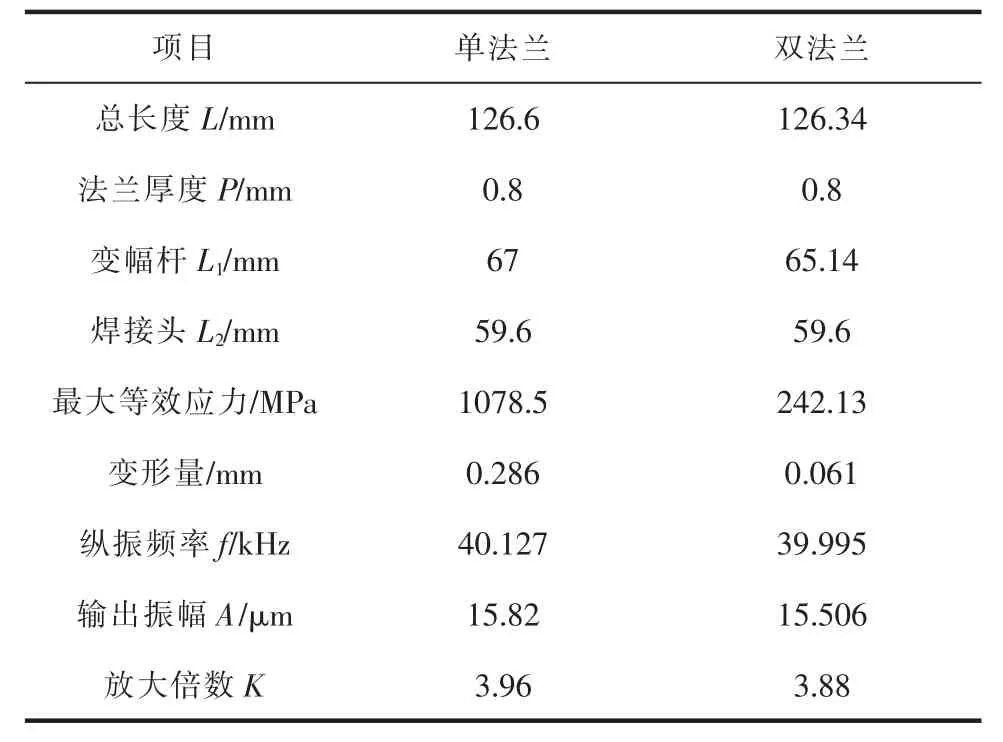
表3 声学组件参数值

3.2 优化结果对比分析

为了验证双法兰声学组件设计的有效性和正确性，本文分别对传统单节点法兰声学组件、优化后的双法兰声学组件进行前述有限元分析，并对结果进行分析比较。 上述两套声学组件的各项参数值见表3。 通过数据对比可发现：

（1）与传统单节点的声学组件相比，采用双法兰结构的声学组件，其在受静压力为500 N 时的最大等效应力和变形量均大幅减小，从而大幅提高了声学组件的结构刚度。 而传统单节点的声学组件在受静压力为500 N 时，其法兰处的最大等效应力已远超材料的屈服强度。

（2）当纵振频率都接近40 kHz 时，在谐振频率下， 双法兰结构声学组件的振幅放大倍数为3.88，小于传统单节点结构声学组件的3.96，但两者相差并不明显，可见双法兰结构声学组件的超声波传递效率并没有下降很多，仍能满足金属焊接的需要。

本文设计的双法兰结构位置虽然并不是处于声学组件的节点位置，甚至是位于声学组件振幅较大位置，但法兰支承上采用多个弧形槽口的结构设计，具有轴向易变形的特点，其对变幅杆形成柔性支承，并不会造成太多能量损耗。

声学系统在焊接过程中因负载变化，其谐振频率会发生偏移，偏移量一般不超过100 Hz。 为避免频率偏移后产生其他振型，需保证纵振与相邻振型的谐振频率之间有较大差值， 通常需大于150 Hz。本文对超声焊接声学组件进行模态分析，得到如表4 所示的纵振及其前、 后阶模态的谐振频率和振动方式。可见，在纵振频率为（39.995±0.160） kHz 范围内无其他振型存在，声学系统受负载影响后的频率偏移不会产生其他振型，故设计的声学组件在振型及频率分布上满足使用要求。

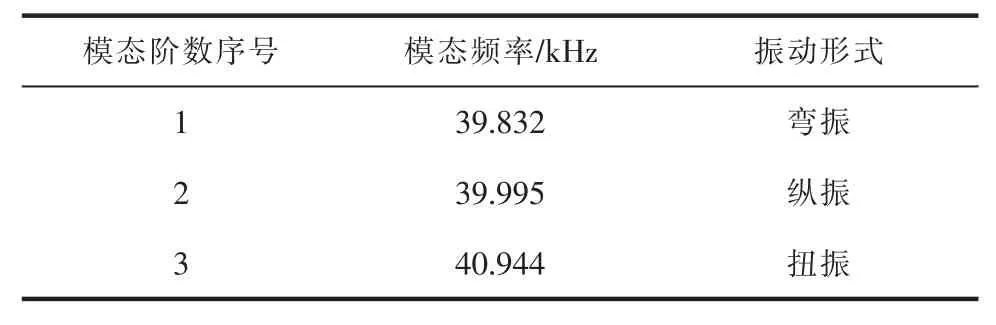
表4 纵振频率及相邻频率振动形式

4 声学系统性能实验

为了验证所设计的双法兰结构是否满足焊接要求并确认设计方法的有效性，通过实验测量了声学系统的谐振频率、阻抗特性、振幅放大倍数等参数。 将声学组件连接频率40 kHz 的压电换能器，声学系统的整体结构见图8。

对声学系统的工具头施加500 N 径向压力，利用PV70A 阻抗分析仪进行阻抗特性分析，所得结果见图9。超声系统在不加压状态下的谐振阻抗最小，在加压状态下的谐振阻抗上升、 反谐振阻抗下降，故超声系统在加压状态的焊接应用中一般都谐振在反谐振频率状态。 可见，声学系统反谐振频率为40.119 kHz， 与理想值40 kHz 的相对误差为0.298%，与有限元分析结果39.995 kHz 的相对误差为0.31%，说明实际频率与设计频率非常接近，满足设计要求。 分析引起偏差的原因是：实验测量的是整个声学系统的谐振频率，但在有限元分析时未考虑换能器的影响，且加工误差也会导致声学系统谐振频率变化，同时法兰的安装圆筒也会对声学系统谐振频率值造成影响。 阻抗分析结果显示，导纳圆是一个规则的圆形，其上下基本对称，动态电阻为87.4199 Ω，机电耦合系数与品质因数均较合适。

实验时， 由数字信号发生器提供超声信号，功率放大器将信号放大，经变压器和匹配箱进行阻抗调节，使传输到声学系统的功率利用率达到最佳状态。本文利用LK-HD 500 激光位移传感器对满足谐振频率要求的声学系统进行振幅实验，分别测量了换能器输出端振幅和焊接工具头的振幅，并以两者之比作为振幅放大倍数。 声学系统振幅实验结果数据见表5。 可知，在有效功率分别为2、4、7 W 的情况下， 声学系统振幅放大倍数分别为3、2.67、2.75，与仿真结果的相对误差分别为23%、31%、29%。 产生上述偏差的原因是：其一，声学组件在振动过程中并不完全是弹性形变，少量的塑性形变也会影响超声波的传递；其二，加工误差产生影响。

表5 声学系统振幅实验结果表

实验结果显示，无径向压力的超声焊接声学系统在有效功率为7 W 时即可输出11 μm 的振幅，满足使用要求。 进一步的实验表明，逐渐增加径向压力，需提升输出功率来克服摩擦力及力负载所引起的能量损耗。 在径向力范围为200～600 N 时，本文设计的声学系统都能通过调节功率条件来保证足够的振幅输出。

5 结束语

本文基于Ansys 数值仿真与单因素实验相结合的方法，进行了超声金属焊接声学系统双法兰结构的优化设计研究。 本文综合考虑超声波传递效率和声学系统结构刚度，提出了一种声学系统双法兰支承设计方案，进行了法兰厚度尺寸对超声传递效率和支承结构刚度的影响规律研究，通过实验对所设计的声学系统进行性能测试。 研究结果表明：利用双法兰作为支承结构的超声焊接声学组件，其振幅放大倍数大于2.5，在满足焊接振幅要求的前提下，其结构刚度大幅提高，解决了超声金属焊接传统单法兰支承结构难以同时满足超声传递效率高和结构刚度强的问题。 通过仿真分析和实验，验证了双法兰结构的有效性，为超声金属焊接声学组件设计提供了新思路。