基于LSSVM-样本熵的车内噪声声品质预测
左言言, 宋文兵, 陆 怡, 顾倩霞, 孙 瑞
(江苏大学 振动噪声研究所, 江苏 镇江 212013)
近年来对于汽车声品质的研究,国内外学者的研究重点都在评价模型上.贺岩松等[1]利用支持向量机算法对加速工况下的车内声品质进行预测,结果表明,支持向量机有很高的预测精度,能够用来预测车内声品质.左言言等[2]对音乐掩蔽下的车内声品质建立了不同的模型,与传统的线型回归相比,基于径向基函数模型的精度更高.刘红星等[3]提出了基于时频分形维数差的声品质评价方法.华敏相等[4]对混合动力汽车进行了基于心理声学客观参量与临界频率带解析小波分解的非稳态车内声品质评价,与其他方法相比取得较好的效果.WANG Y. S.等[5]利用神经网络算法建立了声品质客观量化模型,分析了心理学参数与主观感受的关系.WANG Y. S.等[6]建立了基于人类听觉感知的粗糙度模型,用于静止和非平稳车辆噪声信号以及其他声音相关信号的声品质评价.HUANG H. B.等[7]研究了深度信念网络在车内噪声声品质中的应用,发现DBNs模型的准确性和鲁棒性比传统的预测方法要好,并且其特征融合能力也优于其他的方法.K. L. SANG等[8]提出了whine指数,可以用于电动汽车警报声的声品质评价中.然而这些声品质的建模方法只是基于传统的心理声学等参数,这些参数并不能全面地反映噪声信号的本质特点.笔者提出一种基于LSSVM-样本熵的车内噪声声品质预测.为了建立声品质的评价模型,采集某款混合动力汽车非稳态工况下的噪声信号,进行主客观评价,分别建立基于心理声学参数的评价模型和以样本熵为特征参数的评价模型,并对比两个评价模型在声品质方面的预测性能.
1 噪声信号的采集
选择某款混合动力汽车作为试验样车,偏远郊区作为试验场地,沥青四车道路作为试验路段.在测试地点附近,50 m以内没有声音反射的建筑物和物体,测试时,天气晴朗,温度为20 ℃,微风.根据GB/T 18697—2002 《声学 汽车车内噪声测量方法》标准中的车辆内部噪声测量方法,布置试验条件,利用HEAD SQLab Ⅲ采集系统记录驾驶员以及后排左右的3个位置处不同行驶工况下的非稳态车内噪声信号,采样频率为44.1 kHz.对采集后的信号进行回放筛选,挑选6个工况噪声信号进行评价,共计54个样本,具体信息如表1所示.

表1 非稳态工况的噪声样本信息
2 声品质主观评价试验
对于大多数心理声学评价测试,20名评价者就能够得出较为准确的结果.选取24名均有驾车经验,对车内噪声环境较为熟悉的在校研究生作为评价主体.对评价主体进行听音训练,以统一主观评价的评价标准.选择参考语义细分法作为主观评价试验方法,按照7个评价等级对非稳态工况下的车内噪声品质进行烦躁度评价,评价的描述等级如表2所示.

表2 语义细分法的评价等级描述
由于各主体对声样本的评价尺度存在差别,须对主观评价的试验结果进行评价尺度转换,使得各声样本的烦躁度得分均在同一尺度内,故将语义细分法的主观评价结果转换为10分制,以便于统计分析.对所有主体的评价结果与各声样本的烦躁度得分均值进行相关性分析,去除2个相关系数低于0.7的评价主体的评价结果,统计剩余主体关于噪声烦躁度的评分,最终得到54个声样本的烦躁度评分值如表3所示.
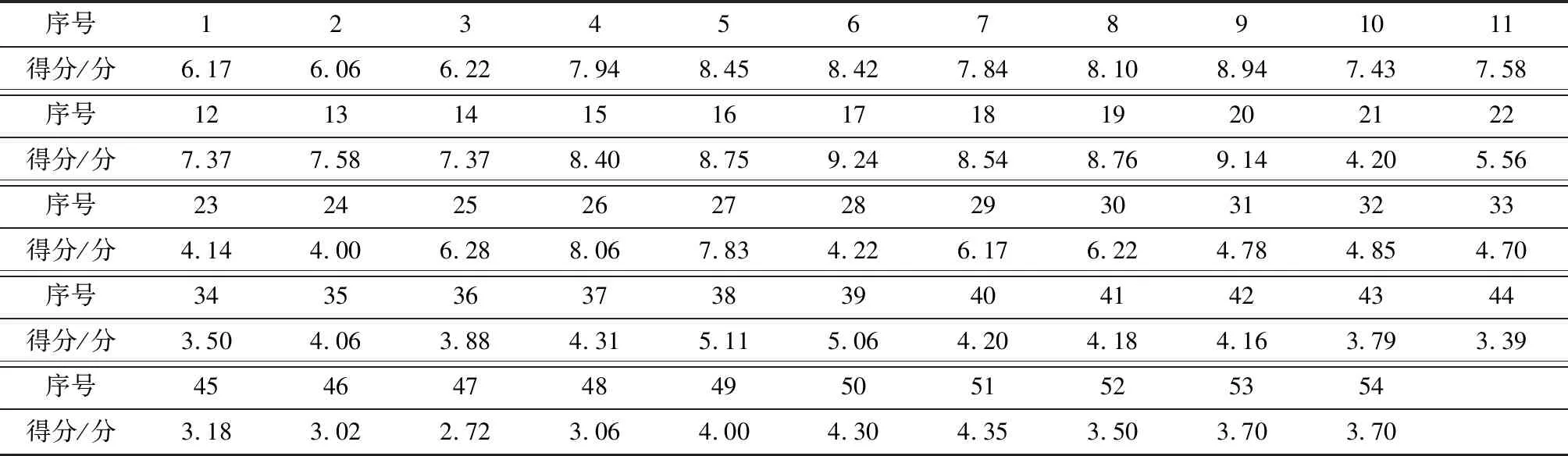
表3 声样本的烦躁度得分
3 客观评价
3.1 客观参数计算
心理声学参数为描述不同噪声造成主观感受差异程度的客观物理量,综合考虑了人体心理反应机制和声学感知特性.选取响度、尖锐度、抖动度、粗糙度、音调度以及语义清晰度(AI)等主要心理声学参数进行分析,同时考虑A级计权声压级和线性声压级的影响,声样本客观参数如表4所示.

表4 声样本的客观参数
3.2 相关分析
利用SPSS软件对声样本的主观评价结果和计算的客观参数进行相关性分析,计算响度、尖锐度、粗糙度、AI指数、抖动度、音调度、声压级、A级声压级8个客观参数与声品质烦躁度得分之间的Spearman相关系数,如表5所示.除了音调度外,其他7个参数与烦躁度间的相关系数绝对值均在0.7以上,其绝对值越小,对烦躁度的影响越小.

表5 主观烦躁度与客观参数间的相关系数
注:**表示双尾检验等级≤0.01.
4 评价模型
4.1 最小二乘支持向量机理论
设一个容量为m的样本集{xi,yi}i=m,对于任意的输入xi∈R,都有对应的输出yi∈R.在非线性映射φ:Rn→F下,将原始的低维数据映射到高维特征空间中,在这个特征空间构造最优线性回归函数[9-11],使得x对应的y都可用f(x)近似表示,即
f(x)=wTφ(x)+b,
(1)
式中:w为权向量;b为常量.
LSSVM算法中的优化问题为
(2)
式中:J(w,ξ)为优化函数;ξ为拟合误差;γ为惩罚因子;φ(·) 为输入空间到高维空间的映射.
引入朗格朗日因子αi,将上述问题转化为
(3)
式中:L(w,b,ξ,α)为优化函数.
根据KKT最优化条件对式(3)进行优化,对w,b,ξ,α求偏导,可得
(4)
消去变量w,ξ,并引入核函数:
K(xi,xj)=φ(xi)Tφ(xj),
(5)
可得矩阵
(6)
式中:l1×m为1×m的单位行向量;lm×1为单位列向量;R1={K(xi,xj)|i,j=1,2,…,m};E为n×n的单位矩阵;α=[α1,α2,…,αm]T;y=[y1,y2,…,ym]T.
根据最小二乘法可求得b和α,可得回归函数:
(7)
4.2 声品质特征参数构造
互补总体经验模态分解(complete ensemble empirical mode decomposition,CEEMD)是A. Y. TYCHKOV等[12]在EMD算法的基础上提出的一种改进的信号分解方法,通过引入正负成对的高斯白噪声来减少模态混叠效应,其计算原理如下:
1) 将n组正负成对的高斯白噪声加入到原信号中,高斯白噪声的幅值是原信号的0.2倍,这样就会产生2n个信号.
(8)
式中:M1,M2分别为加入正、负高斯白噪声后的信号;S为原信号;N为辅助高斯白噪声信号.
2) 将新产生的2n个信号分别进行经验模态分解,各个信号产生1组IMF(intrinsic mode function)分量,cij,cij表示第i个信号的第j阶IMF分量.
3) 对最终得到的IMF进行集总平均获得原信号的IMF分量.
原信号经过CEEMD后的第j阶IMF分量为
(9)
从某种意义上讲,非稳态工况下,车内噪声信号是平稳状态下信息量增加的结果,增加的信息给人的主观感受产生了很大的影响,对声品质的影响很大.而样本熵作为一种量化时间序列复杂性的度量方法,从物理意义上讲是度量序列产生新信息的量,更加全面地反映噪声信号的特点,因此可通过样本熵构造非稳态工况车内噪声信号特征,样本熵的具体计算方法可参考文献[13]中的计算方法.非稳态工况下车内信号特征参数的构造流程如图1所示.

图1 声信号特征参数构造流程图
4.3 非稳态工况下声信号CEEMD分解
对非稳态工况下的声样本进行CEEMD分解,CEEMD分解中的参数取经验值,故加入的高斯白噪声的幅值为原始信号幅值的0.2倍,一共加入200 个高斯白噪声,集总平均次数为200 次,得到非稳态工况下声样本的各阶IMF分量.计算各阶IMF分量与原信号间的相关系数,经过相关分析后,经过CEEMD分解后的信号中与原信号相关性较大的分别是IMF7,IMF8,IMF9,IMF10,IMF11,IMF12这几阶分量,保留对原信号影响较大的几阶IMF分量.非稳态工况1号样本的5-12阶IMF分量如图2所示.分别计算7-12阶IMF分量的样本熵值,结果如表6所示.
从表6可以看出:IMF7-IMF10这几阶分量的样本熵值较大,而IMF11与IMF12这两阶分量的样本熵值较小,相差了几个数量级.故将这6阶IMF分量的样本熵值与主观评价绩效值进行相关性分析,分析各阶IMF分量与主观绩效值间的相关性,分析结果如表7所示.
从表7可以看出:IMF7-IMF10阶分量的样本熵值与主观绩效值的相关性很大,相关系数都在0.9以上,而IMF11与IMF12阶分量的样本熵值与主观绩效值的相关性很低.故在建模过程中不考虑这两阶分量样本熵值得影响.
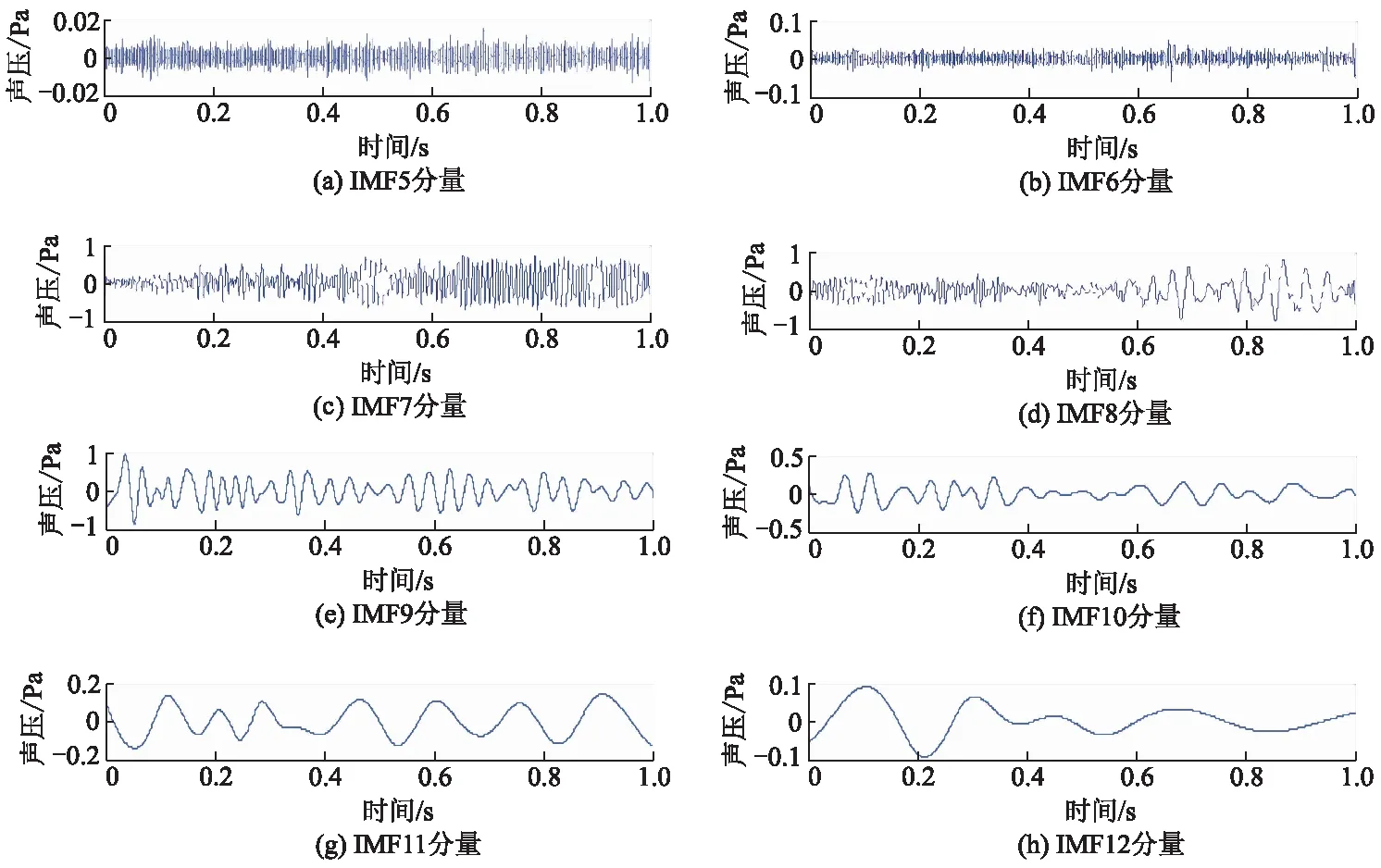
图2 非稳态工况样本1的5-12阶IMF分量
表6 非稳态工况声信号7-12阶样本熵值
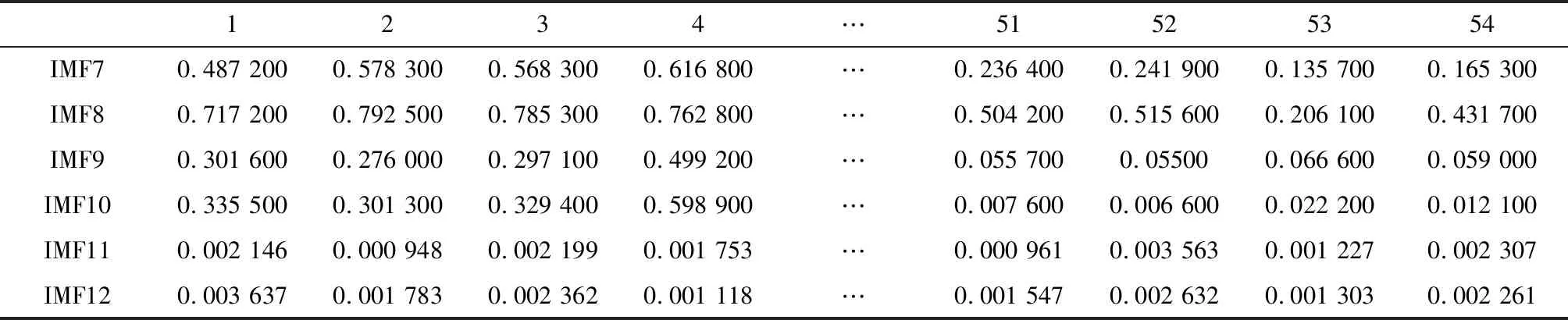
1234…51525354IMF70.487 2000.578 3000.568 3000.616 800…0.236 4000.241 9000.135 7000.165 300IMF80.717 2000.792 5000.785 3000.762 800…0.504 2000.515 6000.206 1000.431 700IMF90.301 6000.276 0000.297 1000.499 200…0.055 7000.055000.066 6000.059 000IMF100.335 5000.301 3000.329 4000.598 900…0.007 6000.006 6000.022 2000.012 100IMF110.002 1460.000 9480.002 1990.001 753…0.000 9610.003 5630.001 2270.002 307IMF120.003 6370.001 7830.002 3620.001 118…0.001 5470.002 6320.001 3030.002 261

表7 各阶分量样本熵与主观评价绩效值的相关系数
5 声品质评价预测模型的建立
5.1 基于心理声学参数的声品质评价模型
利用Matlab中的LSSVM工具箱,以心理声学参数为模型的输入,主观绩效值为模型的输出,建立基于心理声学参数-主观绩效值的评价预测模型.LSSVM模型中,选择径向基函数为核函数,采用网格搜索法对正则化参数gam以及核参数sig进行寻优.将声样本中的1-45号样本划分为训练集对模型进行训练,46-54号样本作为测试集,验证训练后模型的回归预测性能.对训练集和测试集中的参数进行[0,1]量纲一化.模型预测结果如表8所示.
从表8可以看出:基于心理声学的声品质评价模型,在47-51号样本上的预测相对误差在10%以内,其他样本的预测误差均较大,最大超过了33%,总体来说,此模型的预测性能较差.

表8 基于心理声学参数的LSSVM预测结果
5.2 基于特征参数的声品质评价模型
由5.1节的计算结果可知,基于心理声学参数的非稳态工况下声品质评价模型的预测性能较差,无法实现高精度的声品质绩效值预测.由3.2节与4.2节的分析结果可知,心理声学参数与主观评价的相关性相较于特征参数与主观评价的相关性较差.因此,在LSSVM模型的基础上,以特征参数,即IMF分量的样本熵为模型的输入,主观评价绩效值为输出,模型的其他设置与5.1节相同,建立基于特征参数的声品质评价模型,模型的预测结果如表9所示.

表9 基于样本熵参数的LSSVM预测结果
从表9可以看出:以样本熵为特征参作为模型的输入所建立的评价预测模型,其预测误差整体上都较小,最大的相对误差绝对值不超过6%,预测结果明显要好于以心理声学参数为模型输入所建立的评价模型.
5.3 两种评价模型的对比分析
为了验证基于特征参数的评价模型在声品质预测方面的稳定性,统计测试集仿真计算50次预测结果的平均值,并与基于心理声学参数的模型进行对比,结果如图3所示.
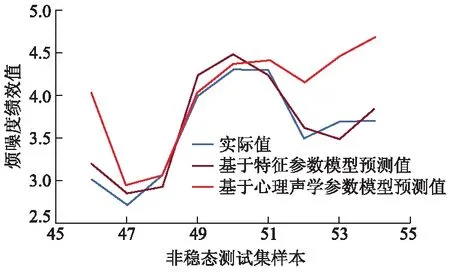
图3 两种模型的预测性能对比
从图3可以看出:两种模型在预测性能上的区别很大,基于特征参数的评价模型的预测性能要明显好于基于心理声学参数的评价模型,其预测结果相对误差绝对值的平均值为3.70%.主要原因在于基于样本熵的特征参数基于信号的能量特征,能够更加全面地反映非稳态工况下声品质特性,虽然心理声学参数可以从某一角度客观量化声品质,但是由于混合动力汽车非稳态工况下的噪声特性比较复杂,导致人在主观评价结果与心理声学参数的相关性不高.因此基于样本熵特征参数的评价预测模型可以用于预测非稳态工况下车内噪声的声品质,预测精度更高.
6 结 论
1) 对采集到的混合动力汽车非稳态车内噪声的烦躁度进行了主客观评价试验,找出了与主观评价结果相关性较大的7个客观参量.
2) 对噪声信号进行了CEEMD分解,找出与原信号相关性较大的几阶IMF分量,并计算这几阶IMF分量的样本熵,构造了新的声品质客观评价特征参数.
3) 利用LSSVM算法分别建立了基于心理声学参数的评价模型和基于样本熵特征参数的评价模型,统计了50次测试集运算结果的平均值,基于特征参数的评价模型的相对误差绝对值的平均值为3.70%,表明用于预测非稳态工况下车内噪声声品质的预测精度更高.

